一类准周期参激非线性扭振系统的周期簇发

时培明，李纪召，刘 彬，韩东颖

(1.燕山大学 电气工程学院，秦皇岛 066004;2.燕山大学 测试计量技术及仪器河北省重点实验室，秦皇岛 066004;3.燕山大学 车辆与能源学院，秦皇岛 066004)

旋转机械是工业部门中应用最为广泛的一类机械设备，在电力、能源、交通、冶金以及国防等领域发挥着无可替代的作用。而传动系统作为旋转机械的核心部分，其运行状态影响整个生产过程。随着生产速度和生产规模的逐步提高，传动系统中的扭振问题也日益突出。传动系统中存在复杂的非线性因素［1］，诸如间隙、非线性阻尼、非线性刚度等［2-4］，导致系统发生非线性扭振，影响其正常工作甚至导致设备损坏，造成重大的经济损失。文献［5］建立含非线性阻尼的非线性转动系统动力学方程，分析其在强迫激励下的近似解。文献［6］对旋转机械传动系统的扭振进行了动力学建模与仿真。

簇发现象在神经元模型中已被广泛地认识［7］。Rinzel［8］首次对神经元的簇放电模式作出了系统的分析，认识到慢变参数对快变量的调节作用引起快变动力学的静息态和激发态的相互转迁。Izhikevich［9］对神经应激性、激发、簇发进行了分析。快慢系统中连接快慢两过程的行为通常称为簇发。Lakrad等［10］研究了自激准周期Mathieu振子的准周期解和簇发现象。Han等［11］对三环面、准周期簇发，对称亚临界hopf/倍周期簇发，亚临界hopf/倍周期簇发，及它们之间的联系进行了分析。季颖、毕勤胜［12］研究了非光滑电路簇发行为的分岔机制及多种簇发现象。

在实际旋转机械的传动系统中，由于间隙、倾角、裂纹等非线性刚度因素的存在，往往以不同频率的周期参数激励的形式同时作用于扭振系统，表现为准周期特性。如裂纹的存在会使转轴刚度发生周期性的变化，从而使转子系统产生含有高频和低频成份的振动，出现复杂的动力学行为［13］。本文考虑准周期参数激励，建立一类含有准周期参激刚度和非线性阻尼的扭振系统的动力学方程。研究了当两种周期激励的频率差距较大时系统的周期簇发现象，给出了周期簇发的参数区域，分析了簇发产生的机制，并对改变快变参激和慢变参激的幅值时所引起的快慢系统的静息态与激发态的变化进行了仿真分析。

1 准周期参激非线性扭振系统动力学方程

旋转机械是工程中广泛存在的动力传动系统，图1为旋转机械中传动系统的两质量扭振系统动力学模型。设J1、J2为扭振系统集中质量的转动惯量，θi(i=1，2)分别为两个集中质量的转角，F1、F2分别是两个集中质量的外加力矩。

图1 二质量扭振系统动力学模型Fig.1 Dynamic model of torsional vibration system with 2-DOF

K为系统的扭转刚度，θ·i(i=1，2)分别为两个集中质量的转速，扭振系统的动能为:

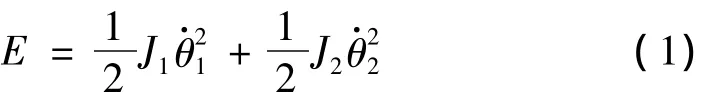
阻尼力表示为:

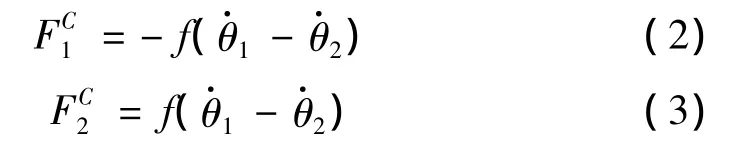
考虑准周期参激刚度，即:

其中，v为与扭振系统固有频率相关的共振频率，Ω为远小于固有频率的慢变频率，ρ'、h'为刚度的变动幅值，K0为等效刚度。扭振系统的势能U为:

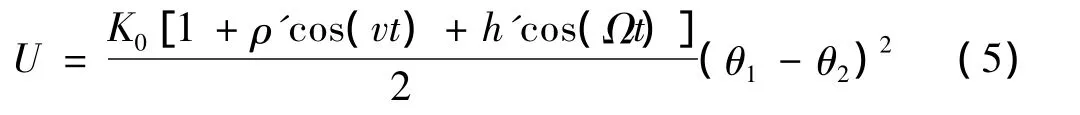
把式(2)和式(3)代入动力学普遍方程

广义力(广义力矩)为:

其中，qr(r=1，2)为广义坐标，n为自由度数目。将式(2)和式(3)代入式(7)后得到系统的广义力(广义力矩)为:

将式(1)、式(2)、式(3)、式(5)、式(8)和式(9)代入如下Lagrange动力学方程:

可得:

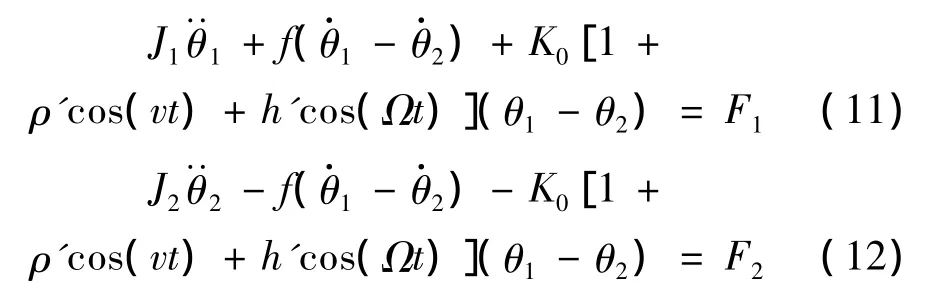
其中，

其中，ω表示系统的固有频率。式(14)就是一类含准周期参激刚度和非线性摩阻的非线性扭振系统的动力学方程。

2 准周期参激扭振系统的分岔响应方程

引入参数ε，对准周期参激扭振系统进行摄动分析。将方程(14)中的参数改写为。则方程(14)可以表示为:

采用多尺度法［14-15］，设方程(15)的摄动解形式为:

将式(16)代入式(15)，可得到各阶近似的线性偏微分方程组:

其中，A(T1，τ)和(T1，τ)为共轭函数且均为关于T1的函数。将式(19)代入式(18)中可以得到:

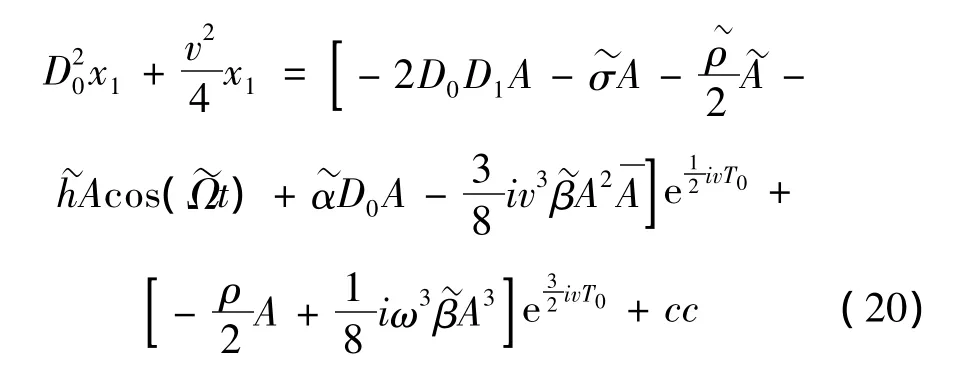
其中，式(20)中cc项表示等式右端各项的共轭复数部分。消除久期项，令:

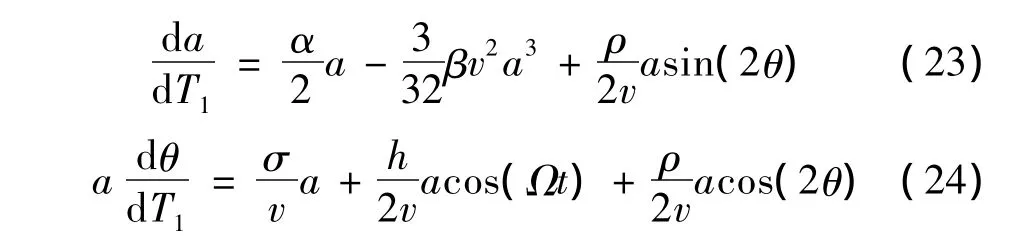
其中，

3 准周期参激扭振系统的周期簇发现象

具有快慢效应的非线性动力系统会产生各种复杂的簇发现象。在静息态和激发态之间的簇发现象会呈现出复杂的动力学特性。当准周期参数激励中其中一个参数激励的频率远小于另一个参数激励的频率时。会发生簇发现象［16］。本文中Ω≪v，系统参数取值为ω=1、α=0.2、β=0.1、σ=-0.2、Ω=0.01。

3.1 快变参激对簇发现象的影响

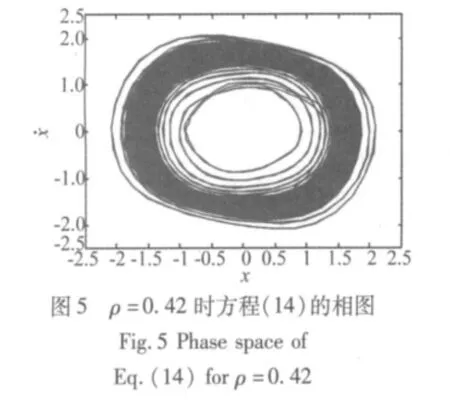
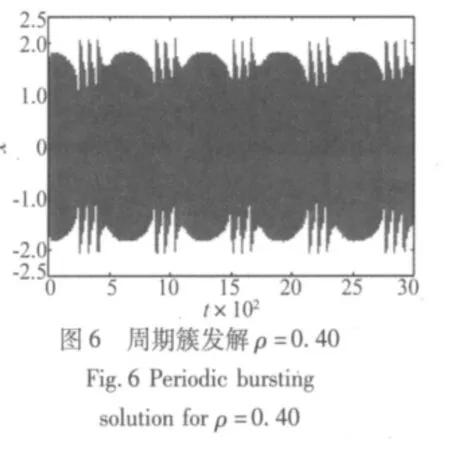
取慢变参激的幅值h=0.02，由于慢变参激项的作用，在分岔响应方程的特性曲线如图2中的区域Ⅰ和区域Ⅱ之间产生了一个区域。在这个区域内取值时，就会发生静息态与激发态的相互转迁，即发生周期簇发现象。将图2中的部分区域进行局部放大如图3所示，当快变参数激励的幅值ρ=0.42时，得到系统的周期簇发解如图4，图中静息态区域较宽，激发态区域较窄并出现一个激发态;减小快变参数激励幅值到ρ=0.4时，系统的周期簇发解如图6，静息态区域变窄，激发态区域增大并出现三个激发态;当快变参数激励的幅值进一步减小到ρ=0.38时，周期簇发解如图8，可以看出，静息态区域继续减小，激发态增加到五个激发态。图5、图7、图9分别为前面的周期簇发解所对应的相空间，从相图中可以明显的看出，静息态位于相图的中间的密集部分，静息态的内侧和外侧为激发态，随着快变参数激励的幅值ρ的减小，静息态的宽度逐渐变窄，激发态开始活跃。

3.2 慢变参激对簇发现象的影响

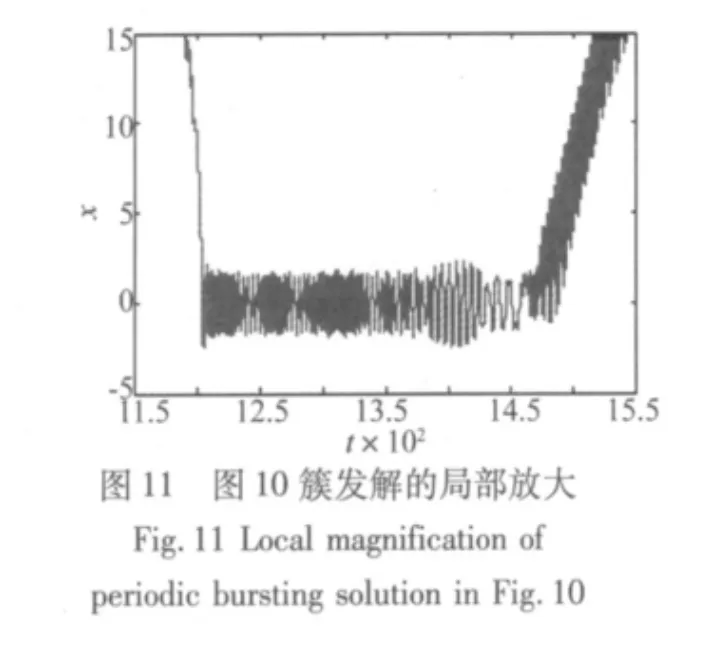
取快变参激的幅值ρ=0.5，当h=2时，准周期参激系统的周期簇发解如图10所示，此时准周期参激系统的动力学特性表现为由相对的大幅值和微小幅值两种振荡的组合，大幅值振荡和小幅值振荡分别看做准周期参激系统的激发态和静息态［17-18］。图11为图10周期簇发解的局部放大，图中，随着时间的推移，会产生双侧不对称的大幅值振荡与小幅值振荡的相互交替现象。周期簇发解所对应的相图如图12，图中系统的运行轨迹为L6→L1→L2→L3→L4→L5→L6，其中的L1→L2及L4→L5段的详细运行规律如图13，图中系统的轨迹为从L1的大幅值振荡开始，跳变进入中心区域的极限环域变为小幅值振荡，然后沿着轨迹L2重新跃变为大幅值振荡。L4→L5段的运行规律与L1→L2段的运行规律类似。

增大慢变参数激励的幅值，当h=3时，准周期参激系统的周期簇发解如图14所示。图15为图14中周期簇发解的局部放大。时序图中，随着时间的推移，会产生单侧不对称的大幅值振荡与小幅值振荡的相互交替现象。周期簇发解所对应的相图如图16，图中系统的运行轨迹为L9→L7→L8→L9，其中的L7→L8段的详细运行规律如图17，图中系统的轨迹为从L7的大幅值振荡开始，跳变进入中心区域的极限环域变为小幅值振荡，然后沿着轨迹L8从极限环中跃变出来重新变为大幅值振荡。

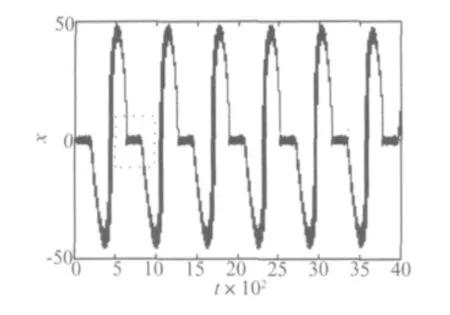
图14 周期簇发解h=3Fig.14 Periodic bursting solution for h=3

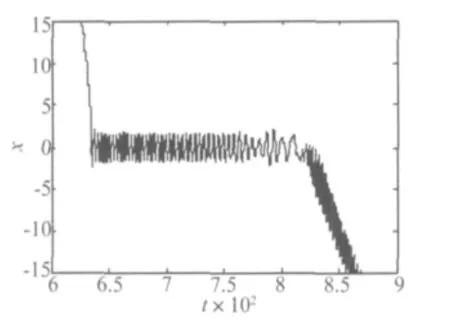
图15 图14簇发解的局部放大Fig.15 Local magnification of periodic bursting solution in Fig.14

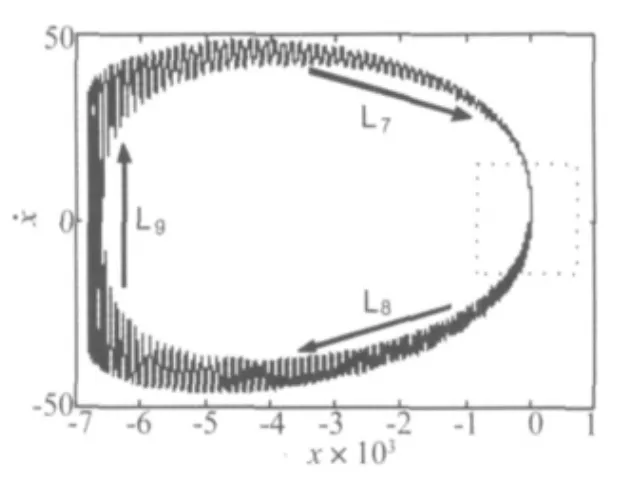
图16 h=3时方程(14)的相图Fig.16 Phase space of Eq.(14)for h=3

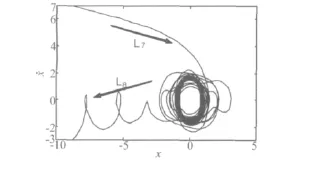
图17 图16相图的局部放大Fig.17 Local magnification of phase space in Fig.16

4 结论

考虑了旋转机械传动系统中两种不同周期参数激励共存的情形，建立了一类含准周期参激刚度、非线性摩擦阻尼的非线性扭振系统动力学方程。求解了系统在1/2亚谐波主参数共振下的分岔响应方程，研究了当两种周期参激的频率相差较大时非线性扭振系统的周期簇发现象，并给出了产生周期簇发的参数取值区域，在区域改变参数取值，就会发生静息态与激发态的相互转迁及周期的改变。当减小快变参数激励的幅值时，静息态的时间减少，激发态区域扩大，簇发所占用的时间延长。当改变慢变参数激励的幅值时，系统的簇发模式及运动轨迹都会发生改变。研究结果为揭示该类旋转机械传动系统中的周期簇发动力行为提供参考。

［1］Christof S.A novel torsional exciter for model vibration testing of large rotating machinery［J］.Mechanical Systems and Signal Processing，2006，20(7):1725-1740.

［2］文 明，王新芳，张维奇，等.阻尼及三次非线性因素对具有调谐质量阻尼器的干摩擦隔振系统性能影响的研究［J］.振动与冲击，2006，25(2):152-158.

［3］李 沈，赵树森.分支轴系扭振的子结构分析方法研究［J］.振动与冲击，2007，26(10):148-151.

［4］史文库，龙 岩，卢玉东.多级非线性双质量飞轮参数设计和优化［J］.振动与冲击，2009，28(5):92-96.

［5］时培明，刘 彬.相对转动非线性动力系统的稳定性与强迫激励下的近似解［J］.物理学报，2007，56(7):3678-3682.

［6］侯东晓，刘 彬，时培明.旋转机械传动系统连续扭振动力学建模与仿真［J］.中国机械工程，2010，21(1):30-34.

［7］Coombes S，Bressloff P C.Bursting:the genesis of rhythm in the nervous system［M］.World ScientificPress，2005.

［8 ］ Rinzel J.Ordinary and partial differential equations［J］.Lecture notes in mathematics，1985，1151:304 316.

［9］ Izhikevich E M.Neural excitability，spiking，and bursting［J］.International Journal of Bifurcation and Chaos，2000，10:1171-1266.

［10］ Lakrad F，Azouani A，Abouhazim N，et al.Bursters and quasi-periodic solutions ofa self-excited quasi-periodic mathieu oscillator［J］.Chaos，Solitons and Fractals，2005，24:813-824.

［11］ Han X J，Jiang B，Bi Q S.3-torus，quasi-periodic bursting，symmetric subHopf/fold-cycle bursting，subHopf/fold-cycle bursting and their relation［J］.Nonlinear Dynamics，2010，61:667-676.

［12］ Ji Y，Bi Q S.Bursting behavior in a non-smooth electric circuit［J］.Physics Letters A，2010，374:1434-1439.

［13］闻邦椿.故障旋转机械非线性动力学近期研究综述［J］.振动工程学报，2004，17(1):1-5.

［14］Shi P M，Liu B，Hou D X.Global dynamic characteristic of nonlinear torsional vibration system under harmonically［J］.Chinese Journal of Mechanical Engineering，2009，22(1):132-139.

［15］刘浩然，张业宽，李晓梅，等.轧机非线性传动系统冲击扭振的研究与抑制［J］.振动与冲击，2010，29(7):179-183.

［16］张晓芳，陈章耀，毕勤胜.周期激励Chen系统的簇发现象分析［J］.物理学报，2010，59(6):3802-3808.

［17］陈章耀，张晓芳，毕勤胜.广义Chua电路簇发现象及其分岔机理［J］.物理学报，2009，59(4):2326-2333.

［18］陈章耀，张晓芳，毕勤胜.周期激励下Hartley模型的簇发及分岔机制［J］.力学学报，2010，42(4):765-773.