MTMD-耗能框架填充墙减震数值分析

黄 炜，王 猛，卢俊龙，何明胜，张程华

(1.西安建筑科技大学 土木工程学院，西安 710055;2.长安大学 建筑工程学院，西安 710061;3.新疆石河子大学 水利建筑工程学院，新疆 石河子 832003)

在传统框架-填充墙结构中，填充墙一般仅起建筑物的围护功能作用，不参与受力，一旦破坏就立刻退出工作，在动力荷载作用下起不到持久的耗能作用。为了充分发挥填充墙在结构抗震中的作用，本文结合结构减振技术，改变填充墙的性能，使其能够在强动力荷载作用下起到耗散能量作用。其原理如图1所示，将主体承重结构与功能围护墙分离，主体承重结构承受竖向荷载，同时也承受水平地震作用，围护墙不仅具有围护建筑物作用，还作为一个质量调谐减震技术(TMD)中的质量块。

图1 控制装置大样图Fig.1 Schematic representation of seismic control

由图1可见，在围护墙顶部设置软钢U型带片作为限位消能元件，围护墙两侧设置脆性抗压件，有关研究可参考文献［12］，底部设置隔振支座，采用双滚轴滚动轴承，隔振支座中装有脆性抗剪件，可调整脆性抗压件与抗剪件的破坏强度，使结构体系在小震作用下，主体结构与围护墙共同提供侧移刚度承担横向荷载，相当于框架填充墙结构;在中、大震作用下，首先脆性抗压、抗剪件发生脆性破坏，围护墙成为一个能左右移动的自由体，形成一个TMD质量块，若具有多片墙体，则形成一个多重调谐质量阻尼器(MTMD)系统。

在底部隔震支座前后两侧采取侧向限位构造措施(见图1(c)所示)，即用矩形钢板作为滑动轨道的挡板;并通过螺栓使软钢U型带片与框架梁可靠连接，因软钢U型带片具有较高的抗拉承载力，可保证在地震时填充墙不出现出平面倒塌或出平面晃动过大伤人。

为了保证减震墙体的减震效果及使用功能，墙体与框架柱的间距应满足相应要求，具体如下:其间距大小为U型金属阻尼器的水平极限位移，一般应小于200 mm，并且200 mm间距对于施工处理较为容易。并在减震墙体立面前后两侧设置保护面板，从而保证墙体的建筑使用功能。

该结构体系把质量调谐减震技术与消能减振技术有机地结合起来，形成一个MTMD减震系统。由于各层围护墙均可作为TMD质量块，则整个系统成为MTMD减震系统，在设计中可大大减少主体结构的截面及配筋。

适用于框架结构的新型MTMD体系，可以有效克服传统围护墙一旦破坏，就立刻退出工作，在动力荷载作用下起不到持久耗能作用的缺陷。本文首先分析MTMD系统的减震原理、参数优化设计方法，以及MTMD计算模型的选取，根据有限元钢框架模型的动力特性设计了MTMD减震装置参数。并建立MTMD-钢框架和普通钢框架结构的计算模型，应用有限元分析软件SAP2000进行动力分析，研究该MTMD减震体系的减震效果。

1 MTMD-结构计算模型及模型选取

1.1 计算模型

研究表明［1-2］，TMD只有当固有频率被调谐到与被控结构自振频率相同或者相近时，才会产生较好减震效果，否则减震效果会骤然降低。此时，只能通过多个TMD来达到覆盖更宽外激励频率，而获得较好减震效果。MTMD系统是由多个TMD组成，与TMD系统相比，具有更宽的响应频率带宽，当主体结构固有频率在不大的范围内波动时，其稳定性明显优于TMD，且控制性能比TMD有较大改善，随着子系统个数N增加，MTMD减震作用更好。如图2所示，MTMD系统为一多自由度体系，主结构为一单自由度体系。并作如下计算假定［3］:

图2 MTMD作用下的结构模型Fig.2 Schematic representation of structure-MTMD system

① 主结构各固有频率呈稀疏分布;② 参数研究时，只考虑一阶模态;③MTMD本身的固有频率呈均匀分布。

MTMD-钢框架系统的动力方程为:

式中，{Ms}、{Cs}、{Ks}分别为主结构的质量、阻尼、刚度矩阵，xs为主结构相对于地面的位移向量，{Md}、{Cd}、{Kd}分别为各TMD组成的质量、阻尼、刚度矩阵。xd为主TMD相对于主结构的位移向量，{N}为各TMD的位置矩阵，{E}为单位向量，{}为地面加速度。

引入变量:

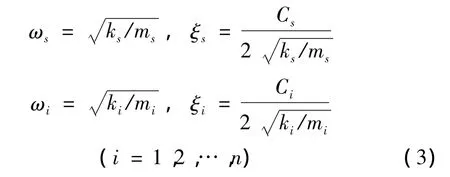
MTMD系统中，每个TMD的频率等分布在受控结构自振频率范围内，设MTMD的平均频率为:

其中n为MTMD中TMD的总数。则第j个TMD的频率增量为:

式中:β为 MTMD 的频带宽。其中ω1，ω2，…，ωn，按频率增大顺序依次命名，则第j个TMD的固有频率可表示为:

定义MTMD系统的调谐比为:

定义MTMD系统的总质量比μ和平均阻尼比ξT分别为:

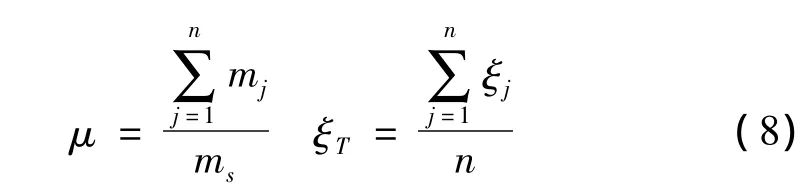
则第j个TMD频率与结构受控频率比可表示为:

那么第j个TMD质量比为:

因此，有:

由于各TMD是在随主结构一起运动的同时产生控制力，因此同步计算主结构和各TMD的反应。假设N层高层结构的第i到j层连续设置n个TMD。将方程(1)和方程(2)合并为一个相互耦合的方程:

式中:

M为结构MTMD系统的质量矩阵，K为结构MTMD系统的刚度矩阵，X为结构MTMD系统的位移向量，C为结构MTMD系统的阻尼矩阵。

为(N+n)维单位列向量。

1.2 模型的选取

Li［5-8］基于MTMD中不同参数的可能组合得到了5种MTMD模型，数值结果表明，具有相同刚度(k1=k2=…=kn)阻尼系数(c1=c2=…=cn)但质量不同(m1≠m2≠…≠mn)的频率线性分布的MTMD能提供较好的有效性和稳定性。此时各个TMD的质量比和阻尼比为:

可以看出，刚度和阻尼保持常量的MTMD最易制作。

2 利用SAP2000模拟及地震反应时程分析

2.1 模型的建立

图3 SAP2000有限元模型Fig.3 SAP2000 FEM model

本文采用验证后的SAP2000有限元数值模型，并以一个3层钢框架结构为算例。因TMD控制结构第一阶模态振动有显著效果，考虑到结构质量和刚度对称性，为防止结构在地震作用下产生较大的扭转效应应，本结构只将顶层两块填充墙做成TMD。模型中的梁、柱采用框架单元模拟，楼板采用Shell单元模拟，假定楼板在其平面内刚度无限大，软钢U型金属阻尼器采用多段线性塑性连接单元模拟，在计算中限定Multi Linear Plastic单元的竖向自由度，保留水平方向的自由度，刚度和阻尼值均为TMD系统的一半。隔振支座采用缝单元(GAP)模拟，在计算中限定GAP单元的竖向自由度，保留水平方向的自由度，刚度和阻尼值均设为零。地震反应分析采用动力时程分析，水平地震作用为X方向。并对比分析普通钢框架和MTMD-钢框架结构的地震反应。

2.2 MTMD-钢框架结构参数的选取

该结构模型如图3所示，为单跨钢框架。构件截面尺寸如表1所示。平面尺寸为1.67 m×1.78 m，总高为3 m，共3层，层高为1 m，模型采用各种型钢焊接组成。钢材均为普通Q235钢。为了防止倾覆，在1-4层上添加了配重。配重为混凝土板，平面尺寸为1 m×1 m，厚度0.1 m。填充墙材料为砖材，墙厚为120 mm，TMD墙外包钢外框采用角钢2L50×5，经计算，每片填充墙质量块m1=m2=185 kg。

表1 梁柱计算参数Tab.1 Computational parameters of beams and columns

为了取得对结构前几阶振型的最佳控制效果，TMD的最佳位置取在拟定控制振型的振型向量中元素绝对值最大者对应的质点处［4］。当考虑控制结构前三阶振型向量最大值对应的位置，对于该结构模型，子结构应设置在结构顶层，主要控制结构的第一阶振型反应。

相关参数计算如下:

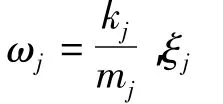
2.3 水平地震作用下动力时程分析对比

为了分析此系统的减震效果，通过将普通框架结构(结构①)与MTMD-钢框架结构(结构②)分别进行计算，具体如下:

时程分析的激励采用两条地震波。一条为适合Ⅱ类场地的EL-Centro(1940，NS)波(即埃尔森特罗地震波，持续时间为30 s，时间间隔0.01 s，最大峰值发生在2.12 s;另一条为适合Ⅳ类场地的天津波(南北向)，持续时间 19.32 s，时间间距为 0.01 s，最大值发生在7.64 s。按照最不利原则，在结构的薄弱方向(即横向)分别输入这两种加速度地震波，时程计算时间都为10 s。地震设防烈度为8°，在罕遇地震下加速度时程曲线的最大峰值为400 gal［9］，计算时将各地震波的加速度峰值均调整为400 gal。

图4 MTMD-钢框架结构示意图Fig.4 The diagram of the MTMD-steel frame

表2 两种地震加速度记录的主要特性Tab.2 The main features of two acceleration

2.3.1 模态分析

通过SAP2000的模态分析功能得到两种结构前三阶振动周期和频率，见表3所示，以及各阶振型图5所示。表中结构①的第二阶振动周期与第一阶相差较大，约为固有周期的1/3，表明结构②的自振特性由第一阶平面内的平动效应主导控制，另外，第二阶振型扭转效应也参与了一部分贡献。与结构①相比，结构②的各阶自振频率相应减少，周期增大了许多。结构②的第一阶周期约为结构①的3倍，结构②的第三阶周期约为结构①的2倍，说明MTMD-钢框架对第一振型的控制效果较好。

图5 MTMD-钢框架结构简化模型分析结果Fig.5 The analysis results of simplified MTMD model

表3 结构自振周期和频率对比Tab.3 Comparison of periods and frequencies

3.3.2 最大绝对加速度

为了便于比较，采用减震率来反映减震效果，定义如下:

图6、图7为在两种不同特性的地震波作用下，两结构各层绝对加速度对比图。图6为EL-Centro(1940，NS)波作用下的j绝对加速度时程曲线对比图，可以看出各层最大绝对加速度都相应的减少。从图6(c)(即顶点绝对加速度时程曲线)中可以看出，结构①的最大绝对加速度峰值为8.565 m/s2，发生在0.7 s，结构②峰值为6.329 m/s2可见，峰值减震率达26.1%，极大地减小了地震反应。图6(a)、图6(b)为两种结构一、二层加速度时程曲线对比图，减震率分别为25.1%和22.9%。

图9 Tianjin作用下结构有无MTMD各层间位移时程曲线(单位:mm)Fig.9 Displacement-time history’s curves of stories with and without MTMD under Tianjin earthquake

图7为在天津波作用下，两种结构各层绝对加速度时程曲线对比图，结构①一、二、三层绝对加速度峰值分别为 3.463 m/s2、3.536 m/s2、3.596 m/s2，均发生在4.1 s。结构②各层最大绝对加速度分别为:3.3 m/s2、3.361 m/s2、3.402 m/s2，减震率 4.74%-5.38%，则天津波作用下，加速度控制效果不明显。

2.3.2 最大层间位移

图8、图9为在两种不同特性的地震波作用下，结构①和结构②各层层间位移对比。图8为EL-Centro(1940，NS)波作用下的位移时程曲线对比图，可以看出各层最大位移均相应的减少。图8(c)中(即顶点位移时程曲线)，结构②峰值为1.612 mm，

结构①的最大相对位移量为2.173 mm，发生在0.7 s;峰值减震率达25.8%，极大地减小了结构地震反应。结构② 一、二层最大层间位移量分别为:1.154 mm、0.509 mm，减震率分别为 22.1% 和 23.1%，减震效果显著。

图9为在天津波作用下，两种结构各层层间相对位移时程曲线对比图，结构①一～三层层间最大位移量分别为 0.389 mm、0.782 mm、1.085 mm，均发生在4.1 s。结构②各层最大层间位移分别为:0.354 mm、0.701 mm、0.963，减震率 9.1%-11.2%，顶层控制效果最好。

同时，从时程分析计算结果亦可看出，在天津波作用下，最大绝对加速度减震率仅为4.74%-5.38%;而在EL-Centro波作用下的减震效果较天津波要好。可见，MTMD-钢框架能够有效地减小结构各层的动力反应(层间位移和最大绝对加速度)，且减震效果亦会受地震波频谱特性的影响。

3 结论

本文对一种应用于框架结构的新型MTMD减震体系的减震性能进行计算分析，具体结论如下:

(1)通过改善传统填充墙的性能，将框架填充墙结构与结构减振技术相结合，使之能够在强动力荷载作用下起到耗散能量的作用。并采取有效的措施，保证该结构不出现平面外的倒塌及结构的建筑使用功能。

(2)MTMD-钢框架结构的振动特性主要由第一阶平面内的平动效应主导控制，第二阶振型扭转效应也参与了一部分贡献。与普通结构相比，第一阶周期放大3倍，第三阶周期放大2倍，则该结构对第一振型控制效果较好。

(3)数值计算结果表明，结构的减震效果在5%-40%之间，有一定的减震效果;若要有效地减小结构各层的水平地震反应，可通过合理选择地震波的频谱特性来实现。

(4)通过计算分析可以看出，合理选择特征参数(质量比、每个TMD的基频、刚度和阻尼)，对MTMD系统进行设计后，MTMD-耗能框架填充墙减震结构体系能够有效地减小楼层的水平地震反应。

［1］李春祥，韩兵康，杜 冬.结构的多重双重调谐质量阻尼器控制策略［J］.振动与冲击，2007，26(2):25-28.

［2］李春祥，熊学玉.地震作用下基于ADMF和系统参数组合的最优 MTMD［J］.计算力学学报，2002，19(3):291-298.

［3］朱金松.高层MTMD控制的布置及地震反应时程分析研究［D］.桂林:广西大学，2008.

［4］苏熔化，梁 冰，宋维源.结构-TMD系统抗震的优化参数研究［J］.振动与冲击，2001，20(4):8-11.

［5］李春祥.地震作用下基于多准则的最优调谐质量阻尼器［J］.上海交通大学学报，2002，36(11):1630-1633.

［6］李春祥.地震作用下高层建筑TMD控制研究与设计［J］.上海交通大学学报，1999，33(6):746-749.

［7］Li C X.Optimum multiple tuned mass dampers for structure under the ground acceleration base on DDMF and ADMF［J］.Earthquake Engineering and Structural Dynamics，2002，31:897-919.

［8］李春祥.基于系统参数均匀分布的新型多重调谐质量阻尼器模型［J］.上海交通大学学报，2005，39(5):775-781.

［9］GB50011-2001，建筑抗震设计规范［S］.北京:中国建筑工业出版社，2001.

［10］张耀庭，刘再华，胡冗冗.新型建筑调谐质量阻尼器的实验研究［J］.工程力学，1999，16(1)34-44.

［11］熊仲明，霍小鹏，苏妮娜.一种新型基础滑移隔振框架结构体系的理论分析与研究［J］.振动与冲击，2008，27(10):124-143.