城市轨道交通高架结构振动与声辐射研究

高 飞，夏 禾，曹艳梅，安 宁

(北京交通大学 土木建筑工程学院，北京 100044)

城市轨道交通日益成为市民出行的重要交通工具，但是高架结构振动与噪声的影响成为制约轨道交通发展的重要因素之一。目前国内外对高架结构的振动影响已有不少的理论成果及试验结果，但是对噪声的相关研究主要集中在轮轨噪声的模拟和计算。然而根据实测情况，当列车通过桥梁时，梁底的噪声水平已经达到70～75 dB(A)，此处噪声基本上是由结构辐射噪声引起的。因此，对于城市轨道交通高架结构的振动及结构辐射噪声影响的研究对于优化结构设计，选择合理的减振降噪措施，促进城市轨道交通发展具有非常重要的意义。

由于复杂结构的振动致声问题一直是工程应用中的难题之一，采用解析的方法求解复杂结构振动辐射声场参数几乎是不可能的［1］。随着数值计算方法的发展，有限元法和边界元法已经成为研究任意复杂结构在外力作用下声振耦合机理的有力工具。用数值计算方法研究高架结构振动和辐射噪声的相关问题，国内外已有不少研究成果，如文献［2-4］应用边界元方法对高架轨道桥进行了噪声场和频谱的计算分析。文献［5］使用结构有限元时程分析与声学间接边界元相结合的方法对移动荷载作用下变截面轨道梁的振动和噪声进行模拟。文献［6］用车桥耦合振动和空气波传播原理提出桥梁振动辐射低频噪声的计算方法。

本文采用有限元方法分别建立了三维桥梁振动分析模型和二维声场分析模型，计算分析了城市轨道交通高架结构振动与辐射噪声声压的频谱规律，研究了结构振动及其辐射噪声之间的相干关系。在此分析的基础上，通过改变桥梁计算参数及行车条件，对结构的振动和辐射噪声水平进行了比较研究。计算分析结果对于新建桥梁的方案设计及减振降噪措施的采用具有一定的指导意义。

1 计算方法

1.1 有限元振动计算理论

使用有限元方法进行桥梁结构振动计算，可以得到在移动荷载作用下结构随时间变化的节点位移、速度和加速度的响应。基本方程为:

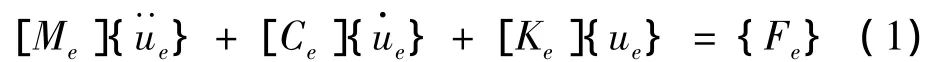
式中:［Me］、［Ce］和［Ke］分别为结构质量矩阵、阻尼矩阵和刚度矩阵，{}、{}和{}分别为结构振动加速度、速度和位移，{Fe}为荷载向量。

对于上述微分方程的求解可采用有限差分法或Newmark法等直接积分法求解。

1.2 有限元声场计算理论

空气与结构在接触面处的相互作用引起了空气扰动并导致了压力变化，也就是说结构的振动引起了其周围声场的产生。接触面处的有限元控制方程为:

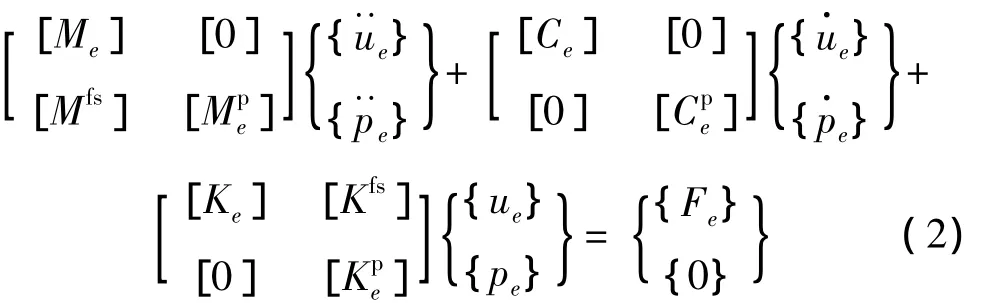
其中:［Mfs］=ρ0［Re］T，［Kfs］=-［Re］。

式中［］、［］和［］分别为空气的质量矩阵、阻尼矩阵和刚度矩阵，［Re］是一个耦合矩阵，代表流体-结构界面上的节点相联系的有效表面面积，ρ0为空气密度，ρ0［Re］为流体-结构界面上的耦合质量矩阵。{p}为压力，而{}和{}分别代表压力变化的加速e度和速度。

本文以下将使用有限元软件ANSYS进行分析计算。

1.3 桥梁计算模型

桥梁结构振动与噪声计算模型采用单线桥梁，为3 m×27 m混凝土连续梁结构，桥梁几何尺寸简图如图1所示，截面形式为单箱单室箱梁，如图2所示。主梁采用C50混凝土，弹性模量为3.55×104MPa，阻尼比取0.05。

相关文献表明［7］:通过和实测结果对比，采用移动荷载模型分析轨道交通桥梁的动力响应分析精度是足够的。因此，本文计算模型中的车辆荷载简化为移动常力。

图1 桥梁几何尺寸简图(单位:cm)Fig.1 Geometry diagram(Units:cm)

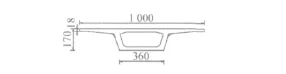
图2 桥梁截面简图(单位:cm)Fig.2 Cross-section of bridge(Units:cm)

1.4 噪声计算模型

城市轨道交通桥梁其延伸方向远远大于其横向宽度，也远大于所考虑的最长波动波长，因此，在高架结构辐射噪声分析中可简化采用二维声场有限元模型。

结构的四周使用流体单元包围以建立二维空气场区域，为模拟无限空间，空气区域的外壳使用无限吸收单元建立边界条件。数值试验已确定当吸收单元远离结构或振动源区域以外大约0.2λ能产生准确的结果。其中，λ=c/f为声波的主波长，c是流体中的声速，f是声波的主频。本文模型经初步计算，声波的主频范围为4～5 Hz，声速c取340 m/s，则空气区域的边界取以梁截面顶板为圆心，半径为25 m的圆形，如图3所示。

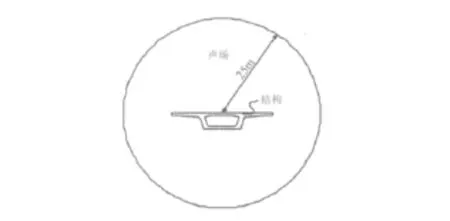
图3 声场计算简图Fig.3 Sound field calculation diagram

2 计算结果分析

2.1 振动特性

表1给出了部分自振频率和振型计算结果。根据前5阶振型可以看出，连续梁桥主要以竖向振动为主。

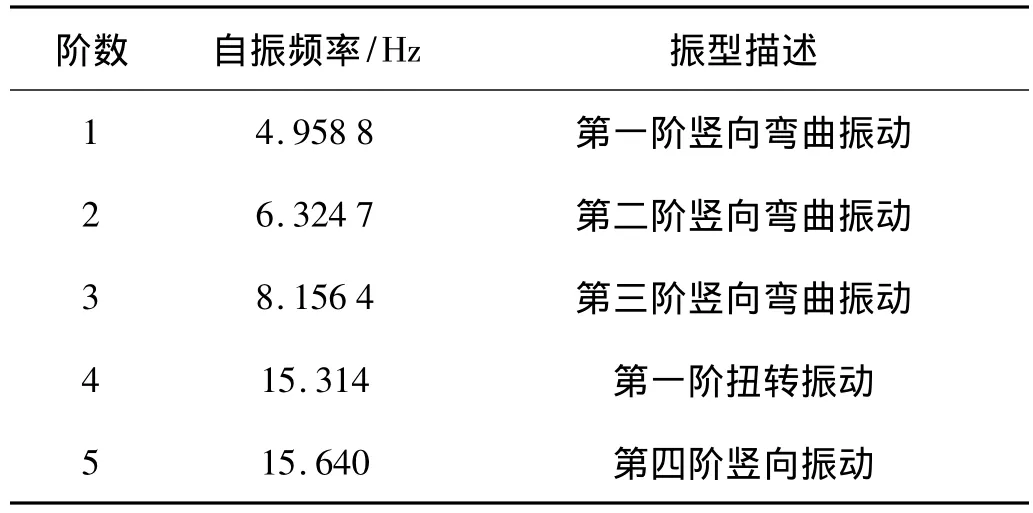
表1 桥梁结构自振频率Tab.1 Natural Frequency of bridge

2.2 振动结果分析

2.2.1 振动频谱分析

由辐射声压的Helmholtz积分公式可知，辐射声压受结构表面法线振速的直接影响，因此，通过使用快速傅里叶变换得到了结构竖向振动速度响应频谱图，用来研究高架结构的振动频率成分以及分布情况，如图4所示。

由图4可以看出，当列车以60 km/h的速度通过桥梁时，振动速度响应峰值主要集中在4.5～8.75 Hz和32.5～34.15 Hz之间，而桥梁的前三阶自振频率包含在4.5～8.75 Hz之中。由此可以看出，桥梁的竖向振动响应频率以低频为主，主要是由结构的前几阶竖向振动自振频率决定。

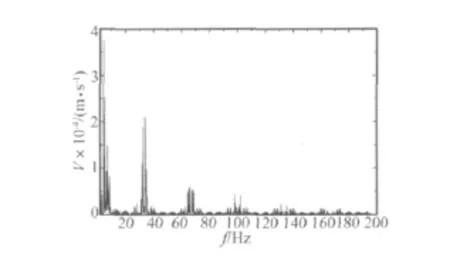
图4 振动频谱图Fig.4 Spectrogram of vibration

2.3 噪声结果分析

一般频率为20～20 kHz的可听声波为噪声控制研究的主要对象，但是医学专家通过研究发现，人体内器官固有频率基本上在低频和超低频范围内，很容易与低频声音产生共振，因此，低频噪声对人体部分器官可能造成功能性损害及器质性损害。同时，为研究振动与噪声之间关系的方便，本文也对频率为20 Hz以下的次声波进行了分析研究。

通过有限元计算，可以得到由结构竖向振动引起的与梁底紧密接触的空气压力(即线性声压)变化时程响应，通过使用傅里叶变换得到其频谱分布如图5所示，由计算结果可知声压幅值出现在32.6 Hz处，为0.09 Pa。

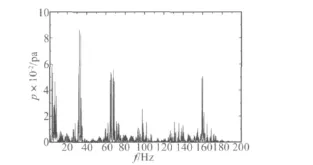
图5 声压频谱图Fig.5 Spectrogram of sound pressure

结合结构竖向振动响应频谱图可以看出，声压频谱与振动响应频谱前几阶峰值分布基本相同，但在声压频谱160 Hz附近出现一个明显的峰值，分析认为空气质点的竖向振动不但受到结构振动的激扰，还会受到空气体积变化的影响。因此，在进行结构辐射噪声计算中，以结构表面法向振速和声阻抗率来表示声压，就会引起一定的误差。

3 相干性分析

通过相干性分析，可以确定不同频率的声压有多大程度来自于桥梁结构振动，即声压和振动的相关程度。

由图6中的相干性分析可以看出，对于连续梁桥，90 Hz以内大部分频段相干函数值较高，最大值在84.7 Hz，为0.94;90～200 Hz频段内只有个别频率处的相干函数值较大。

因此，对于连续梁桥降低90 Hz以内的结构振动将直接有效减小结构辐射噪声水平，而对于其他频段的辐射噪声采用控制噪声传播途径的方法可得到有效的控制。

4 计算参数影响研究

4.1 桥梁阻尼

阻尼是反映结构体系振动过程中能量耗散特征的参数，是影响结构振动响应的重要因素之一，阻尼的存在能够改善结构的振动状况，因此研究高架结构的阻尼特性对振动与噪声的影响研究具有一定的意义。

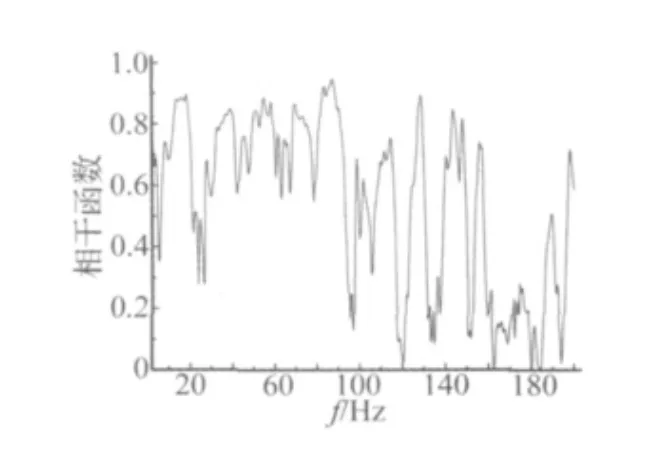
图6 相干性分析Fig.6 Coherence analysis

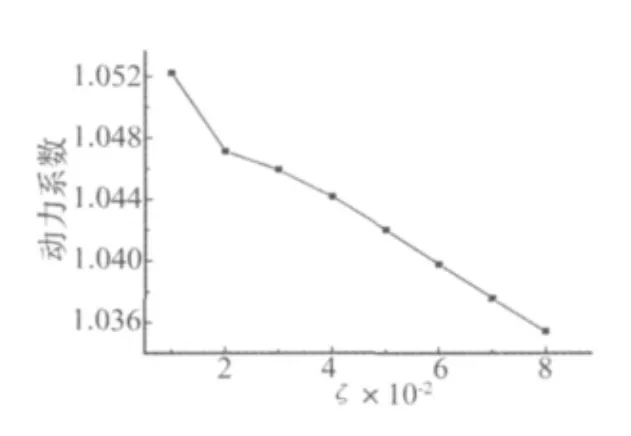
图7 不同阻尼比下的动力系数Fig.7 Dynamic coefficient with different damping ratio

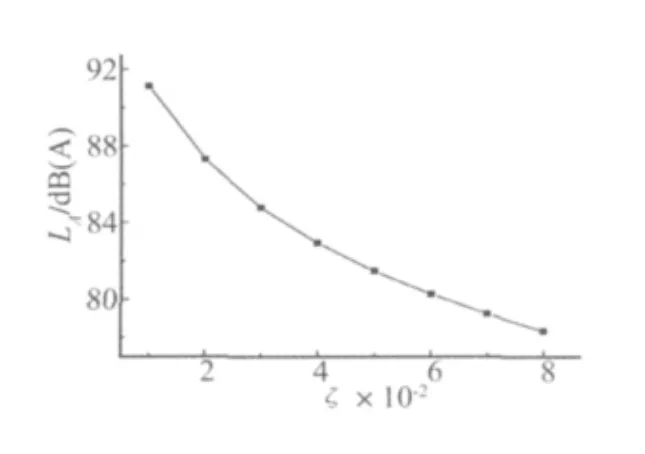
图8 不同阻尼比下的辐射声压级Fig.8 SPL with different damping ratio

桥梁阻尼比ξ的取值范围为0.01～0.08，中跨跨中动力系数及梁底的A计权声压级随阻尼比的变化如图7和图8所示。

由图中可以看出，对于相同荷载作用下的连续桥梁，结构的动力系数和辐射噪声水平随着阻尼比的增大而减小，阻尼比从0.01增大到0.08，动力系数降低了1.6%，声压级减小了12.8 dB(A)。因此，结构阻尼比的增加将在一定程度内大大减少结构的振动与辐射噪声水平。

4.2 支座刚度

表2中编号1～6为文献［8］提供的具有不同形状系数的铅芯橡胶支座竖向刚度的实验数据，以此为参数分别计算具有不同支座刚度的桥梁中跨跨中动力系数及梁底的A计权声压级，如图9、图10所示。

表2 支座刚度k取值Tab.2 Value of support stiffness

由图中可以看出，支座刚度在200.43～417.44 MN/m范围内时，随着刚度的增加，桥梁动力系数有所减小，但随着支座刚度的继续增加，动力系数不断增大，动力系数最大变化值为1.66%。梁底的辐射A声级随着刚度的增加而增大，在刚度达到649.21 MN/m后有减小的趋势，但声压级最大变化值仅有0.7 dB(A)。

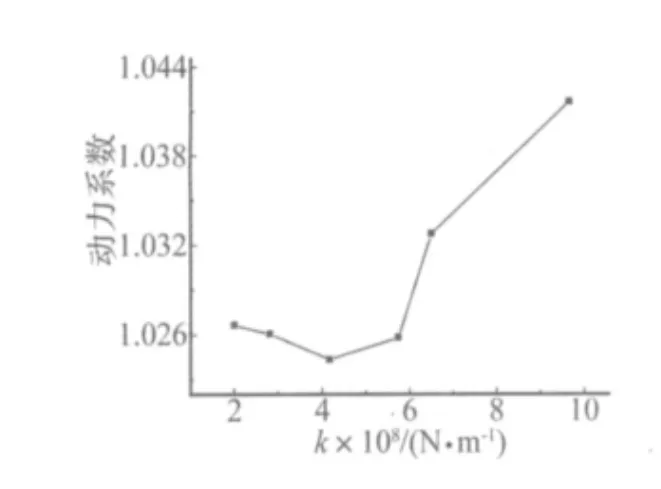
图9 不同支座刚度下的动力系数Fig.9 Dynamic coefficient with different support stiffness

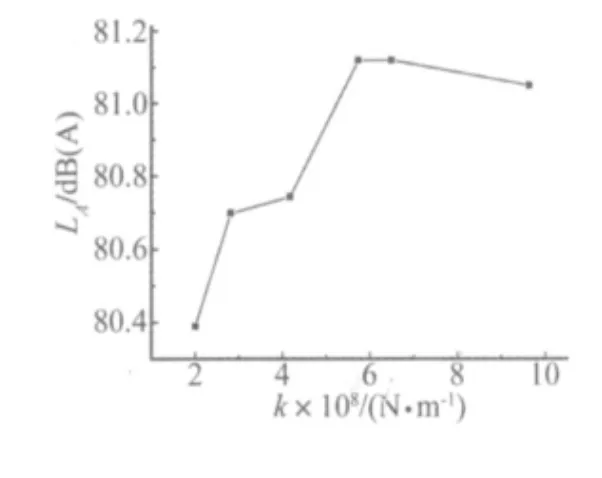
图10 不同支座刚度下的辐射声压级Fig.10 SPL with different support stiffness

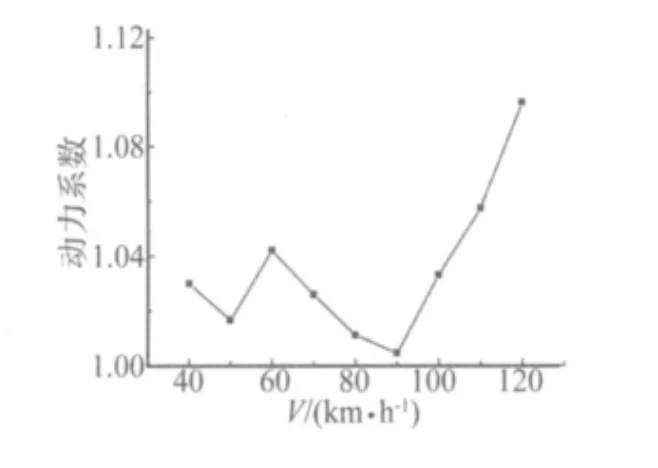
图11 不同车速下的动力系数Fig.11 Dynamic coefficient with different speed

因此，选择合适刚度的桥梁支座能够改善连续梁桥的动力响应，但对结构辐射噪声的影响很小。

4.3 行车速度

城市轨道交通的车辆速度一般在40～120 km/h范围内，因此研究该速度范围对结构振动与噪声的影响具有现实意义。图11给出了不同车速下的动力系数的计算结果。

移动荷载的周期性排列，会对桥梁结构产生周期性作用，因此加载频率对结构的振动响应产生重要影响。由图11中的计算结果可以看出，桥梁的动力系数随着车速的增大呈波动性增加，车速为90 km/h时，动力系数达到最小值。图12反映了梁底辐射噪声水平随车速变化的情况。可以看出，车速在40～70 km/h范围内，辐射声压级随车速的增加而略有增大;车速在70～120 km/h范围内，辐射声压级随车速的增加波动变化，车速为80 km/h时，辐射声压级最小，为80.97 dB(A)，车速为100 km/h时，辐射声压级达到最大值82 dB(A)。由于声压级的差异在1.02 dB(A)以内波动，因此40～120 km/h范围内的车速变化对结构噪声的影响较小。

4.4 车辆荷载

移动荷载列的荷载值由每节车厢及转向架的重量平均分摊到每个轮对上计算得到。车辆荷载取值范围如表3所示，其中工况1和工况5分别为空载和满载，插值得到工况2～工况4。

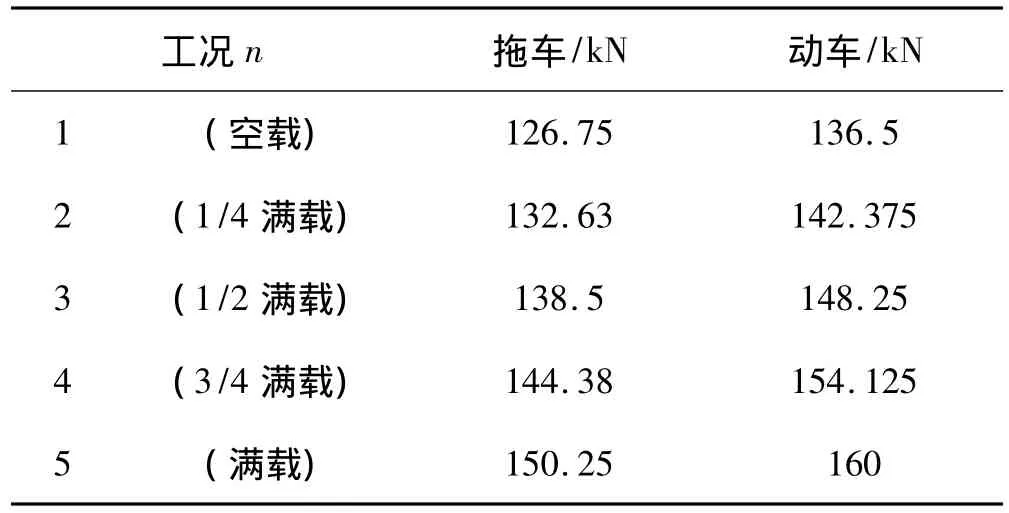
表3 车辆荷载取值(轮下荷载)Tab.3 Value of vehicle loads(loads under wheels)

不同工况下计算的结构动力系数如图13所示，动力系数变化随着荷载的增加变化很小。由图14可以看出，随着荷载的增加，梁底辐射声压级呈线性趋势增加，满载工况比空载工况增大约1.4 dB(A)。

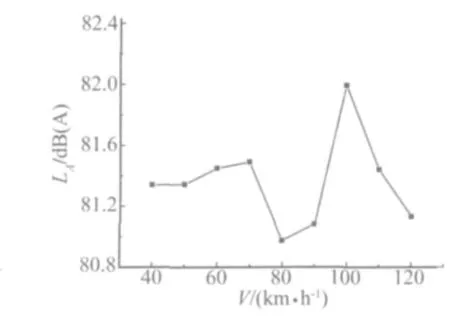
图12 不同车速下的辐射声压级Fig.12 SPL with different speed

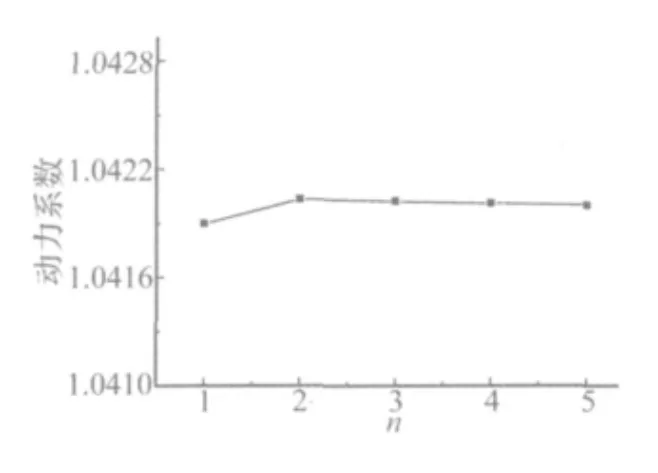
图13 不同车辆荷载下的动力系数Fig.13 Dynamic coefficient with different loads

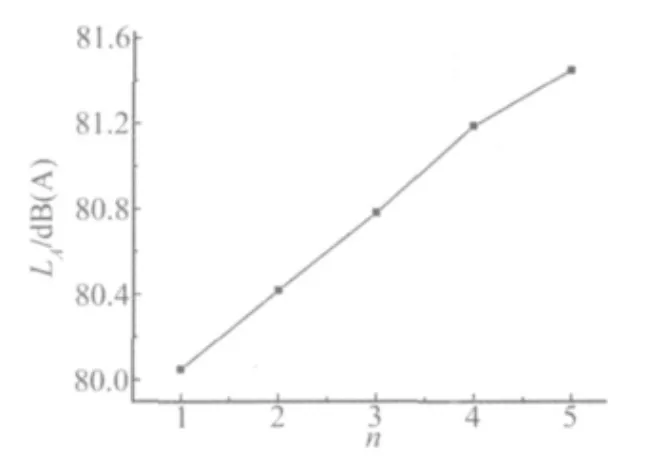
图14 不同车辆荷载下的辐射声压级Fig.14 SPL with different loads

5 结论

(1)当列车以60 km/h的速度通过连续梁桥时，桥梁的竖向振动响应频率以低频为主，主要是由结构的前几阶竖向振动自振频率决定。

(2)对于连续梁桥控制90 Hz以内的振动水平，将直接有效的控制结构振动与噪声对环境的影响。

(3)桥梁结构的阻尼比对结构的振动响应及辐射声压级影响显著，随着阻尼比的增大，声压级最大可减小 12.8 dB(A)。

(4)支座刚度变化对结构振动响应影响较大，但对降低结构辐射噪声效果不够明显。

(5)桥梁的动力系数随着车速的增大呈波动性增加，车速在40～120 km/h范围内的变化对结构噪声的影响较小。

(6)动力系数变化随着移动荷载的增加变化很小，梁底辐射声压级呈线性趋势增加，满载工况比空载工况增大约1.4 dB(A)。

［1］郭 骅，姜 哲.关于辐射效率σrad的讨论［J］.振动工程学报，1992，5(2):133-139.

［2］ Jean P.A variational approach for the study outdoor sound propagation and application to railway noise［J］.Journal of Sound and Vibration，1998，212(2):275-294.

［3］ Jean P，Gabilletusing Y.A boundary element approach to study small screens close to rails［J］.Journal of Sound and Vibration，2000，231(3):711-719.

［4］朱 彦，陈光冶，林常明.城市高架轨道桥辐射噪声的计算与分析［J］.噪声与振动控制，2005，25(3):37-41.

［5］胡新伟，黄醒春.高架轨道梁振动与结构噪声的数值模拟［J］.低温建筑技术，2007(2):54-56.

［6］谢 旭，张 鹤，山下幹夫，等.桥梁振动辐射低频噪声评估方法研究［J］.土木工程学报，2008(11):53-59.

［7］高传伟，唐雅茹，余 华.基于移动荷载过桥的轨道交通桥梁振动研究［J］.中国铁道科学，2005，26(2):73-76.

［8］吴 彬.铅芯橡胶支座力学性能及其在桥梁工程中减、隔震应用的研究［D］.北京:铁道科学研究院，2003.

［9］杨新文，翟婉明，和振兴.轨道板声辐射特性［J］.中国铁道科学，2009，30(1):24-28.

［10］赵志高，黄其柏，何 锃.基于有限元边界元方法的薄板声辐射分析［J］.噪声与振动控制，2008(1):39-43.

［11］雷晓燕，王全金，圣小珍.城市轨道交通环境振动与振动噪声研究［J］.铁道学报，2003，25(5):109-113.

［12］何正嘉，訾艳阳，张西宁.现代信号处理及工程运用［M］.西安:西安交通大学出版社，2007.