基于声辐射模态有源解耦控制的溢出机理研究

田晓光，姜 哲

(江苏大学 振动噪声研究所，江苏 镇江 212013)

由结构振动引起的声辐射问题一直是声学领域重要的研究课题。Fuller等［1］提出有源结构声学控制(Active structure acoustic control，ASAC)后，国内外许多学者围绕这个问题进行了广泛的研究。其中利用结构模态展开研究已经取得了丰硕的成果，但是因为各阶结构模态声辐射的相互耦合，使得在有些频率下即使削减了某几阶主要的结构模态的幅值，也不能保证结构辐射声功率的降低［2］。黎胜、赵德友［3］讨论了结构振动模态耦合对声功率的影响并解决了声辐射模态公式中特征频率解得不唯一问题。上世纪90年代初，有学者提出了用声辐射模态来研究结构辐射的声功率［4-6］，各阶模态声辐射之间没有相互耦合，很适合研究结构振动引起的声辐射问题。李双、陈克安［7］研究了结构模态与声辐射模态之间的对应关系。毛崎波等［8］利用声辐射模态提出了针对控制前k阶声辐射模态降低声功率的控制策略。李双等［9］在声辐射模态基础上研究了作动器的位置对控制效果的影响。靳国永等［10］通过声辐射模态建立了弹性封闭空间声辐射有源控制模型。黎胜、赵德友［11］讨论了以刚性表面和柔性表面为界的半空间内的辐射问题。吴经彪等［12］提出了基于声辐射模态有源控制解耦，在简支矩形板上利用作动器的布放位置使得控制过程解耦。

本文在声辐射模态主动控制的基础上进行研究，对比解耦和不解耦两种控制方式，发现解耦控制所需控制能量小，控制简单，稳定。两者在频率较低时都能取得良好的控制效果，在频率较高时都会出现控制溢出。通过分析各阶声辐射模态辐射效率，作动器布置位置对称形式与声辐射模态对称形式的对应关系，揭示了解耦控制溢出的机理。

1 基于声辐射模态的有源控制解耦

由声辐射理论可知，声辐射模态是辐射体表面的一种可能的辐射形式，是给定辐射物体所固有的性质，由辐射体的几何形状和激励频率决定，与辐射体本身的材料特性无关［6］。各阶声辐射模态相互正交，每阶声辐射模态对应一个独立的辐射声功率，辐射的总声功率可以表示为:

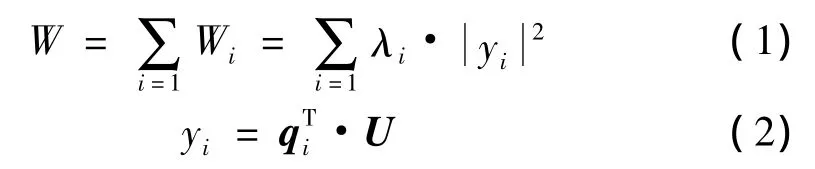
其中:qi表示第i阶的声辐射模态;U为结构表面振速;yi是第i阶声辐射模态的伴随系数，是结构表面振速在对应声辐射模态上的投影;Wi表示第i阶模态对应的声功率;λi与实对称正定矩阵的特征值成正比。各阶声辐射模态的辐射效率为［8］:

其中:ρ为介质密度，c为介质中的声速，Δs为划分的单元面积。

声辐射模态在各阶时，对应的辐射效率随着阶数的增加而迅速降低［8］。前几阶声辐射模态辐射的声功率在总的声功率中占据绝对大的分量。引入控制力改变结构的表面振速分布，在低频时，如果能够使得前k阶辐射模态伴随系数同时为零，控制后结构总的声功率必然会大幅降低［8］。即:

假设在原始激励力作用下板的法向振速写成Up，在控制力下的板的法向振速写成Uc，根据叠加原理表面法向振速U可以写成［8］:

用压电陶瓷片为作动器提供控制力，施加控制电压E(t)，板的振动响应写成:

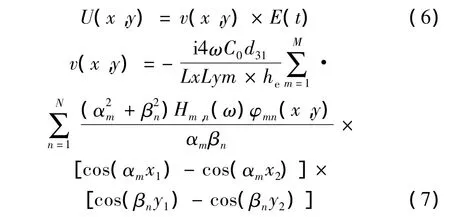
v(x，y)是作动器施加电压与板的表面振速之间的传递函数［13］。式中i为虚数单位是板的质量密度;d31为压电应变常数;M、N为考虑的般的结构振动模态数;C0为应变–弯矩耦合常数;Lx和Ly为板的长和宽;he为压电片厚度;x1，x2，y1和y2分别对应压电片位置的横、纵坐标的最大值和最小值，同时反映压电片的大小。αm=mπ/Lx;βn=nπ/Ly;φmn(x，y)=sin(αmx)sin(βny)为板的结构振动模态;Hm，n(ω)=(ω2m，n-ω2+i2ξm，nωωm，n)-1，称为频响函数;ξm，n为模态阻尼比系数。

在控制力作用下板的法向振速为:

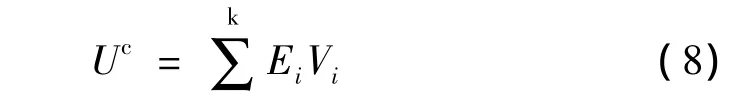
其中k表示控制力个数，Vi为第i个作动器在施加控制电压Ei的传递函数向量，由式(7)确定。

将式(5)，式(8)代入式(4):得到k个方程组成的方程组，可以解得k个控制电压。输入控制电压，就能控制前k阶模态辐射的声功率。

取k=4，图1表示任意布置4个(组)压电陶瓷片作动器 PZTI、PZTII、PZTIII、PZTIV 位置。坐标下标第一位为作动器标号，第二位为压电片的横、纵坐标的最大值和最小值。由方程(9)解得4个输入控制电压，可以控制4阶声辐射模态辐射的声功率。由于方程(9)是耦合的，需联合求解方程(9)得到各个控制电压Ei。因此，作动器在控制过程中相互影响，相互制约，使得作动器有多余的动作，导致输入能量大，控制系统不稳定。并且控制效果随着作动器位置的变化而变化，无法确定最优布放位置。这就是非解耦控制方案。

图2表示解耦控制4组(9个)作动器PZT1、PZT2、PZT3、PZT4布置位置［12］。第1组作动器 PZT1是将1个压电陶瓷片粘贴在矩形板的中心，陶瓷片的两中心线与板的两中心线重合;第2组作动器PZT2是将2个规格相同的压电陶瓷片关于x=0.5Lx对称粘贴，两陶瓷片中心线与y=0.5Ly重合，分别以幅值相等，相位相反的电压驱动;第3组作动器PZT3是将2个规格相同的压电陶瓷片关于y=0.5Ly对称粘贴，两陶瓷片的中心线与x=0.5Lx重合，分别以幅值相等，相位相反的电压驱动;第4组作动器PZT4是将4个规格相同的压电陶瓷片关于x=0.5Lx、y=0.5Ly对称粘贴，其驱动电压幅值相等，相对相位如图所示。在实际应用中，可将压电陶瓷片的电极对应相反连接，从而提供幅值相等相位相反的控制电压。由于四组作动器是基于前4阶声辐射模态的对称性布置，从而这4组作动器能分别独立激励前4阶声辐射模态的辐射模态，有［12］:

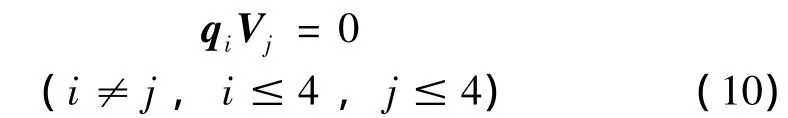
将式(10)代入式(9)，取k=4，方程组变成4个独立的方程，解方程可以得到4个独立的控制电压:

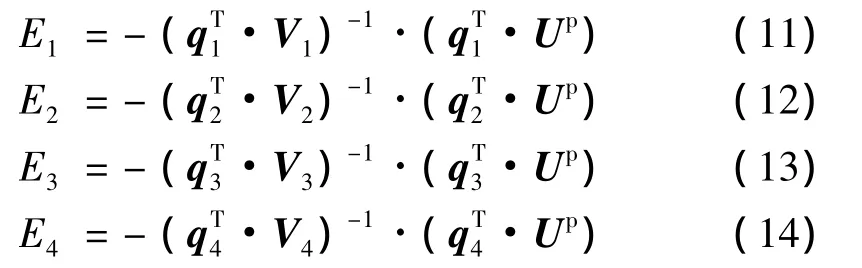
输入4个相互独立控制电压控制4组作动器，抵消前4阶模态辐射的声功率，此即解耦控制策略。

对于非解耦控制，如果一组作动器不能正常工作，由于作动器之间的耦合，会导致其余三组作动器都不能正常工作，不仅没有控制效果，反而会导致辐射声功率增大。解耦控制时4组作动器互相独立工作，即使某一组作动器不能工作，也不会对其他三组作动器产生影响，仍然会对其他三阶模态的声辐射有控制效果。从而使系统的稳定性、可靠性大大增加。并且能够方便的查到出现故障的作动器，使得故障诊断更加容易。

解耦输入控制能量表示为:

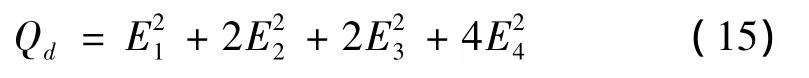
非解耦控制输入能量表示为:

其中Ei是在不同方案下的控制电压。

2 解耦控制与非控制解耦比较

设简支板参数为:长Lx=0.36 m，宽Ly=0.3 m，厚度h=0.002 m，弹性模量Eb=2 ×1011N/m2，ρ=7.8 ×103kg/m3，泊松比vb=0.3，各阶模态阻尼系数均为0.01;设压电陶瓷各项参数为:长La=0.05 m，宽Lb=0.05 m，厚度he=0.4 mm，弹性模量Ee=6.3 ×1010N/m2，泊松比ve=0.3，压电应变常数d31=1.66 ×10-10m/V，原始激励力用压电陶瓷片提供，激励电压为10 V，取板左下角为坐标原点，压电片中心点坐标为(0.054，0.045)。

解耦控制方案:作动器布置在图2所示位置。非解耦控制方案一:4个作动器中心位置分别为(0.185，0.158)、(0.28，016)、(0.157，0.26)、(0.06，0.06);非解耦控制方案二:4组作动器中心位置分别为(0.10，0.12)、(0.23，0.17)、(0.18，0.22)、(0.05，0.03)。两种方案作动器的位置是随机选取。

图3是0～1 000 Hz控制范围内的三种控制方案的控制结果。通过对比可以发现，在600 Hz以内，三种方案都可以取得良好的控制效果，600 Hz以上，三种控制方案出现了不同程度的溢出。并且非解耦控制时，作动器位置对控制效果会产生明显的影响。

图4表示三种方案在低频时输入控制能量比较。解耦控制方案要明显好于非解耦的控制方案，输入控制能量小，并且控制能量在各个频率段相差不大，更加稳定。

3 解耦控制溢出机理分析

由式(1)、式(3)可知，声功率可以表示为声辐射模态伴随系数与其对应的辐射效率的线性组合。图5是前8阶声辐射模态的辐射效率图，在频率较低时(低于600 Hz)，对应的辐射效率随着声辐射模态阶数的增加而迅速降低［8］。在低频时，高阶模态的辐射效率远远低于低阶模态，因此高阶模态辐射声功率占总辐射声功率的比重很小，对控制效果的影响可以忽略不计。在频率较高时，高阶模态辐射效率很大，高阶模态声辐射占总声辐射的比重很大，高阶模态对控制效果的影响也会随之变得很大。

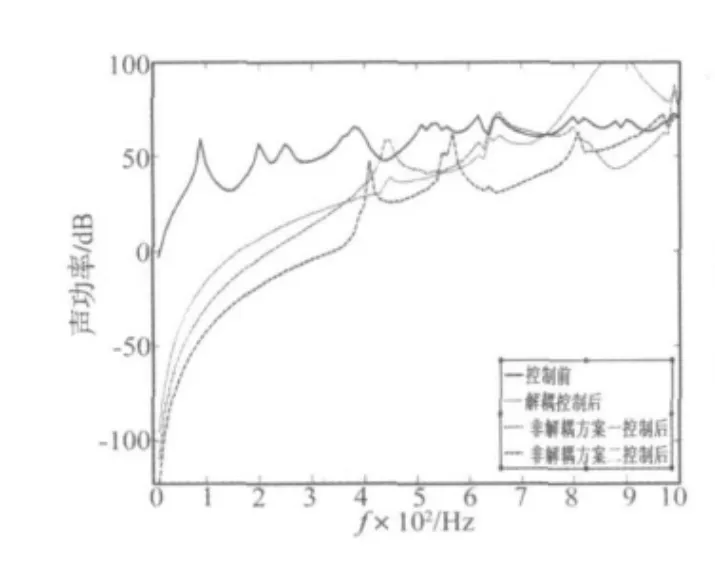
图3 三种方案控制结果比较Fig.3 The control results of three programs

图4 三种方案控制能量比较Fig.4 The control energy of three programs

图5 板的前八阶声辐射模态辐射效率系数Fig.5 The radiation efficiencies of the first eight radiation modes

图6表示了前4阶声辐射模态具有4种互相独立的对称形式［12］，图2所示4组作动器就是基于这种对称形式进行布置的，把前4阶模态对应的对称形式分别称为第一、二、三、四种对称形式。通过分析声辐射模态，发现很多高阶模态也拥有这4种对称形式。图7表示了五到八阶模态的形状。可以看出，第5阶、6阶声辐射模态具有第一种对称形式，第7阶声辐射模态具有第三种对称形式，第8阶声辐射模态具有第二种对称形式。

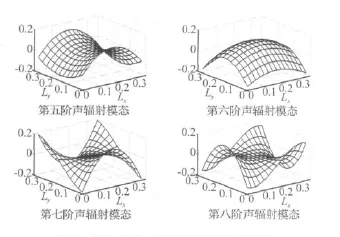
图6 板的前四阶模态形状Fig.6 The mode shapes of the first four radiation modes on the panel

图8表示了第一组作动器激励的5～8阶声辐射模态的伴随系数，其中第5、第6阶模态伴随系数很大，第7阶、8阶模态伴随系数很小。图9和图10表示了第二组、第三组作动器的情况。可以发现，第一组作动器不仅激励第一阶声辐射模态［12］，而且激励第5阶、第6阶声辐射模态。第二组作动器不仅激励第2阶声辐射模态［12］，而且激励第8阶声辐射模态。同样，第三组作动器可以激励出第3阶、第7阶声辐射模态。每组作动器对有相应对称形式的模态都有较大的激励。

图11～图14表示了解耦控制后，5～8阶模态辐射声功率的变化情况。可以发现，5～8阶模态辐射效率在控制后，在某些频率段出现积极的控制效果，某些频率段则出现消极的控制效果。

频率较低时，由于高阶模态的对控制效果影响可以忽略，此时即便产生消极的控制效果，其辐射的声功率还是很小，不会产生控制溢出。而频率较高时，高阶声模态辐射声功率很大，对控制效果的影响很大，此时产生消极的控制效果，就会出现控制溢出现象。

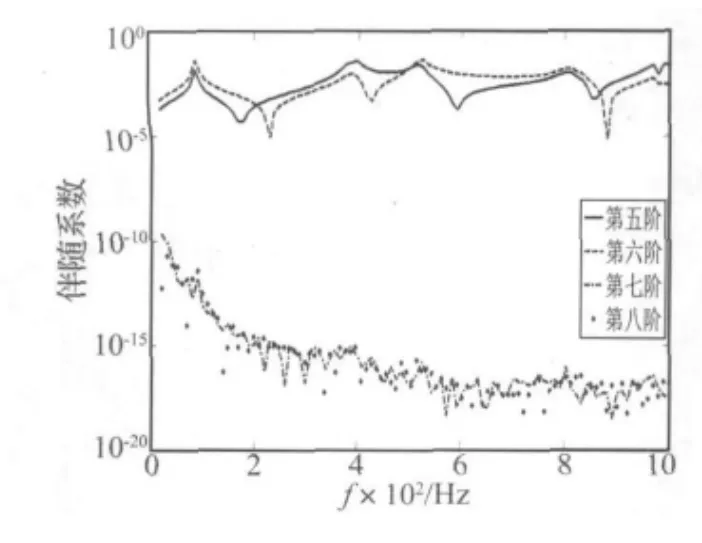
图8 PZT1激励的5～8阶声辐射模态伴随系数Fig.8 The adjoint coefficients of the radiation modes from five to eight excited by PZT1

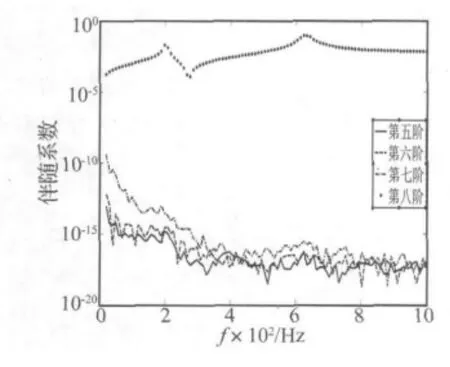
图9 PZT2激励的5～8阶声辐射模态伴随系数Fig.9 The adjoint coefficients of the radiation modes from five to eight excited by PZT2

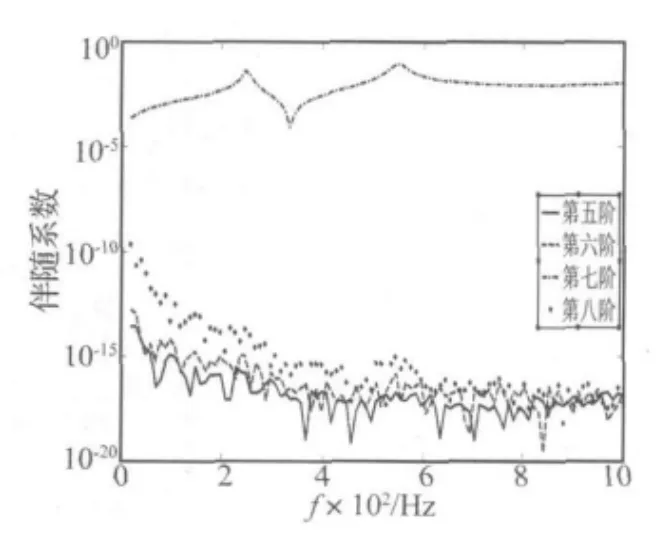
图10 PZT3激励的5～8阶声辐射模态伴随系数Fig.10 The adjoint coefficients of the radiation modes from five to eight excited by PZT3

可见，当高阶声辐射模态对称形式与作动器布置的对称形式一致时，控制策略仅针对前4阶声辐射模态进行控制，由于作动器对有相同对称形式的高阶模态的激励，以及高阶模态声辐射占总声辐射的比重的增加，造成了高频段出现控制溢出。因此在较高频率时，为避免控制溢出，在制定控制策略时应兼顾考虑高阶声辐射模态的影响。

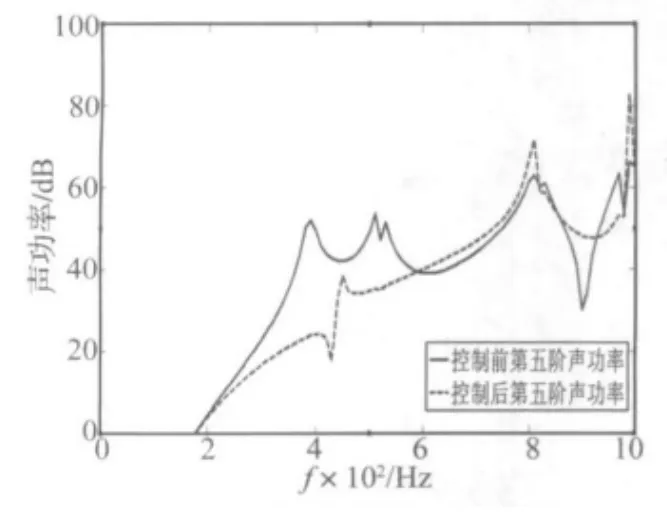
图11 解耦控制前后第5阶声辐射模态辐射声功率Fig.11 The sound powers of the fifth radiation mode before and after decoupling controlled

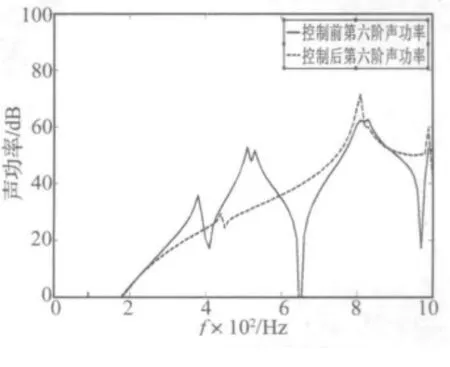
图12 解耦控制前后第6阶声辐射模态辐射声功率Fig.12 The sound powers of the sixth radiation mode before and after decoupling controlled

图13 解耦控制前后第7阶声辐射模态辐射声功率Fig.13 The sound powers of the seventh radiation mode before and after decoupling controlled

图14 解耦控制前后第8阶声辐射模态辐射声功率Fig.14 The sound powers of the eighth radiation mode before and after decoupling controlled

4 结论

本文通过比较基于声辐射模态的解耦和非解耦两种控制方法，得到解耦控制的优点:各组作动器可以独立激励出对应阶的声辐射模态辐射的声功率，作动器位置确定，输入的控制能量小，控制系统更加稳定可靠，故障诊断更加容易。

600 Hz以内，解耦控制和非解耦控制两种方法都能取得良好的控制效果，没有明显的控制溢出。600 Hz以上，两种控制方案都会出现不同程度的控制溢出。重点分析了解耦控制下的溢出机理。

在比较高的频率，为了避免控制溢出，有必要对解耦控制进一步发展新的控制策略，控制前4阶模态时，兼顾考虑5～8阶的影响。

［1］Fuller C R.Optimal placement of piezoelectric actuators and polyvinylidence fluride error sensors in active structural acoustic control approach［J］.J.Acoust.Soc.Am ，1992，92(3):1521-1533.

［2］ Snyder S D ，Tanaka N.On feedforward active control of sound and vibration using error signals［J］.J.Acoust.Soc.Am，1993，94(4):2181-2193.

［3］黎 胜，赵德友.结构声辐射的振动模态分析和声辐射模态分析研究［J］.声学学报，2004，29(3):220-208.

［4］Borgiotti G V.The power radiated by a vibrating body in an acoustic fluid and its determination from boundary measurements［J］.J.Acoust.Soc.Am，1990，88(4):1884-1893.

［5］Cunefare K A，Currey M N.On the exterior acoustic radiation modes of structures［J］.J.Acoust.Soc.Am.，1994，96(4):2302-2312.

［6］ Elliott S J，Johnson M E.Radiation modes and the active control of sound power［J］.J.Acoust.Soc.Am，1993，94(4):2194-2204.

［7］李 双，陈克安.结构振动模态和声辐射模态之间的对应关系及其应用［J］.声学学报，2007，32(2):171-177.

［8］毛崎波，姜 哲.通过声辐射模态研究结构声辐射的有源控制［J］.声学学报，2001，26(3):277-281.

［9］李 双，陈克安.结构声辐射有源控制中主导辐射模态的抵消及次级力的最优布放［J］.噪声与振动控制，2006(6):62-66.

［10］靳国勇，刘志刚，卢熙群，等.通过辐射模态研究封闭空间结构声辐射及其有源控制［J］.哈尔滨工程大学学报，2009，30(4):376-382.

［11］黎 胜，赵德友.半空间内声辐射的研究［J］.船舶力学，2004，8(1):106-112.

［12］吴经彪，姜 哲，朱利锋.基于声辐射模态的有源控制解耦［J］.声学学报，2009，34(5):453-461.

［13］ Dimitriadis E K，Fuller C R，Rogers C A.Piezoelectric actuators for distributed vibration excitation of thin plates.ASME Transactions［J］.Journal of Vibration and Acoustics，1991，113:100-107.