基于蚁群算法的航空发动机失谐叶片减振排布优化分析

袁惠群，张 亮，韩清凯，宋 琳

（1.东北大学 理学院，沈阳 110819；2.东北大学 机械工程与自动化学院，沈阳 110819）

航空发动机叶盘结构通常具有循环对称性质，但由于加工误差、材料性质等原因，每个叶片的特性不可避免地存在微小差异，即失谐［1］。失谐破坏了结构的循环对称性，导致其振动能量集中在一个或几个叶片上，使这些叶片的振幅达到其他叶片振幅的几倍，造成局部叶片的高周疲劳失效［2-6］，对整个结构的正常运行构成严重威胁，因此如何采取有效措施减小失谐引起的振动局部化现象，非常具有实际意义。文献［7-10］以叶盘静力学配平为目标，分别采用退火单亲算法、遗传算法及改进的遗传算法对叶片的排列顺序进行优化；文献［11-12］通过设计有效的主动失谐方式，运用遗传算法和序列二次规划混合优化方法确定了失谐叶片的最大幅值放大系数及相应最坏失谐模式的通用方法。设计主动失谐对降低系统受迫振动的共振幅值有利，但共振区变宽，系统更容易产生共振。在设计时引入大频差失谐，加工得到的失谐叶片虽不能与设计失谐量完全一致，只要误差控制在一定范围内，能够达到降低系统受迫振动共振幅值的目的，在理论研究与工程应用中都有重要价值；文献［13］针对既定失谐叶片，引入蚁群算法以降低模态局部化程度为目标对失谐叶片安装顺序进行优化，克服了遗传算法计算时间长，编码复杂的缺点，并取得了较好的优化结果。本文在文献［13］基础上，以有效降低叶盘系统受迫振动幅值、减轻系统振动局部化程度为目标，对叶片排列顺序进行优化分析。

1 叶盘振动分析模型及动力学方程

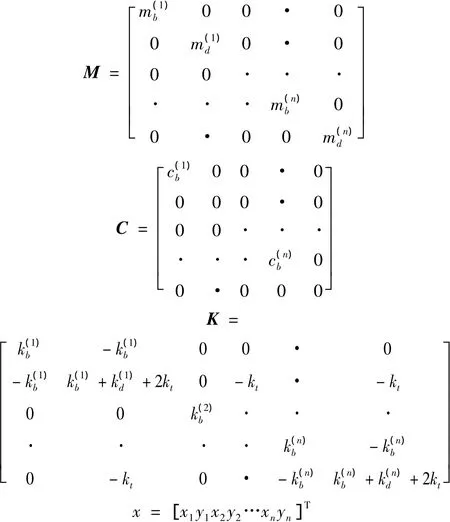
为了便于分析叶片排布对失谐叶盘振动情况的影响，尤其是对受迫振动幅值和各叶片振动幅值差异的影响，建立了叶盘系统的集中参数分析模型，如图1所示。该模型可以方便进行结构参数调整，以分析不同叶片排布下系统的振动情况。本文模型中物理参数均采用无量纲参数，并取叶片数n为36，其中mb为叶片质量、md为轮盘质量、kb为叶片刚度、kd为轮盘刚度以及kt为轮盘耦合刚度，下标“i”表示第i扇区的参数。谐调叶盘模型采用文献［14］中的物理参数，如表1所示。模型失谐因素只考虑叶片刚度失谐。

图1 叶盘系统集中参数模型Fig.1 Lumped parameter model of blade-disc system

表1 谐调系统模型参数Tab.1 Modal parameters of tuned system

当系统为谐调状态时，有kbi=kb，kdi=kd。考虑叶片刚度失谐后，叶盘模型各叶片刚度可表示为：

式中Δki为第i叶片的刚度失谐量。

叶盘系统的动力学方程为：

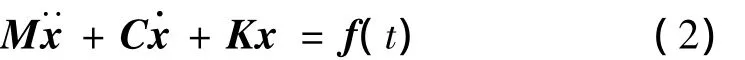
式中x为位移向量，M，C，K，f（t）分别为质量、阻尼、刚度矩阵和激振力向量，具体的质量、阻尼、刚度矩阵，位移向量如下：

2 叶片排布对失谐叶盘系统振动的影响

假设叶片刚度失谐量Δkbi随机分布，本文取其为均值为0，标准差为1%的一个随机样本，各叶片对应的刚度失谐量Δkbi列于表2。

表2 各叶片刚度失谐量Tab.2 Amount of stiffness mistuned of every blade

在分析叶盘受迫振动响应时，在叶片上施加简谐激振力，不妨设载荷幅值为1，

设，

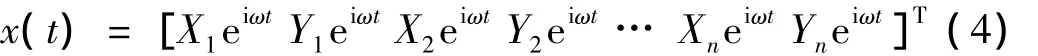
顺次安装该组叶片（定义为失谐1），选取叶片的阻尼系数ξ=0.002，得到此时系统受迫振动最大振幅如图2，图中左图为各叶片振幅在对应激振频率下的最大值，右图为激振频率从0.9到1.15变化时各叶片的最大振幅，下文各图相同。该失谐条件下各叶片最大振幅平均值为106.864 6，各叶片最大振幅的方差为376.931 0，各叶片最大振幅最大值为160.553 0。

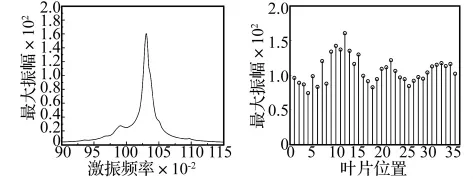
图2 失谐1条件下系统受迫振动最大振幅Fig.2 Maximum amplitude of forced vibration under mistuned 1

将上述叶片随机排布，顺序如下（失谐2）：［17，7，8，28，34，10，6，23，26，30，36，18，33，25，32，27，5，35，24，13，1，21，4，22，11，29，12，20，2，16，3，14，15，19，31，9］。在激振力向量不变的情况下，得到失谐2时系统受迫振动最大振幅如图3，该失谐条件下各叶片最大振幅最大值为164.489 3，方差为 430.603 5，各叶片最大振幅平均值为107.529 2。

由以上分析可知，在各叶片失谐刚度不变的情况下，叶片安装排列顺序可以影响系统的振动情况，所以一定存在一种或几种叶片安装排列顺序能够使一组既定的失谐叶片达到该组叶片的最佳振动，本文将采用蚁群算法对叶片排布进行优化，找到使叶盘系统受迫振动幅值降低、系统振动局部化程度减轻的叶片排布。

图3 失谐2条件下系统受迫振动最大幅值Fig.3 Maximum amplitude of forced vibration under mistuned 2

3 叶片排布优化模型的建立与分析

3.1 基于蚁群算法的叶片排布优化模型建立

对于失谐叶片-轮盘系统，评价一种振动的优劣，通常采用叶片最大振幅作为评价指标。本文综合考虑各叶片最大振幅的平均振动水平和各叶片最大振幅的差异水平，即各叶片最大振幅的平均值、方差作为指标来进行评判。提出振动局部化参数如下：

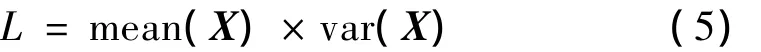
式中：X为各叶片最大振幅向量，mean（X）为各叶片最大振幅平均值，var（X）为各叶片最大振幅方差。

本文运用人工蚁群算法，以L为目标函数，对失谐叶盘系统各叶片进行了优化排布。对于n个叶片，每个叶片对应固定的序号1，2，…，n，m为蚂蚁的数目，某时刻叶片i与j之间连接的信息素用τij（t）表示。τij（t）的初始值τij（0）为人为设置的正常数c，每只蚂蚁可以选择下一个叶片，每只蚂蚁移动到下一个叶片的时刻变为t+1。经过n-1次移动后，每只蚂蚁都将完成一次路径的搜索，这时的时间将是t+（n-1）。所有蚂蚁经过的路径中最短的一条，即能使振动局部化参数最小叶片排列顺序将被保存下来。同时叶片之间上的信息素浓度也将更新为：

其中，ρ（0≤ρ＜1）表示信息素的持久性，即残余信息的保留部分。

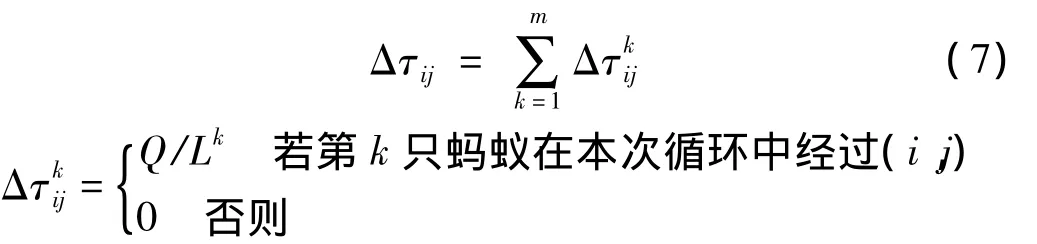
其中：Q是常数，用来表示蚂蚁完成一次完整的路径搜索后，所释放的信息素总量；Lk为通过第k只蚂蚁选择的一组叶片排列顺序计算得到的振动局部化参数。

以上蚂蚁选择叶片的过程中，第k只蚂蚁从叶片i转移到叶片j的概率定义为：

其中，tabu（k）表示第k只蚂蚁在此时刻还没有访问过的叶片集合；α表示信息素浓度的相对重要程度。

表3 蚁群算法具体参数Tab.3 Concrete parameter of ant colony algorithm

如此反复计算直到达到所指定的循环次数NCmax，其算法的流程图如图4所示。本文蚁群算法采用具体参数见表3，参数选取依据文献［15］。

3.2 优化结果分析

通过人工蚁群算法优化，得到的叶片最佳排布为：［6，8，21，36，15，18，5，10，11，7，14，27，29，12，34，24，35，9，1，31，25，4，2，19，30，3，22，13，23，26，33，20，32，16，17，28］。此时，系统受迫振动最大振幅如图5，该失谐条件下最大叶片最大振幅为127.593 8，各叶片最大振幅方差为70.039 2，平均值为111.343 3。由图5与图3、图4比较及表4知：

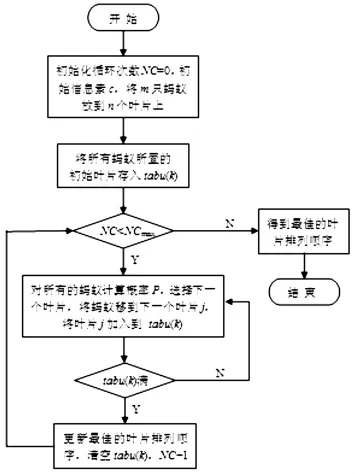
图4 蚁群优化叶片排列顺序流程图Fig.4 Flowchart of blade arrangement optimized by ant colony algorithm

（1）通过人工蚁群算法可以找到失谐叶盘系统叶片排布的适当顺序，使得叶盘系统的振动得到较大改善；

（2）通过叶片优化排列可以使失谐叶盘系统振动局部化程度有效减弱，但较谐调系统相比，仍存在局部化现象。

图5 经叶片排布优化的叶盘系统受迫振动最大幅值Fig.5 Maximum amplitude of forced vibration under blade arrangement optimized

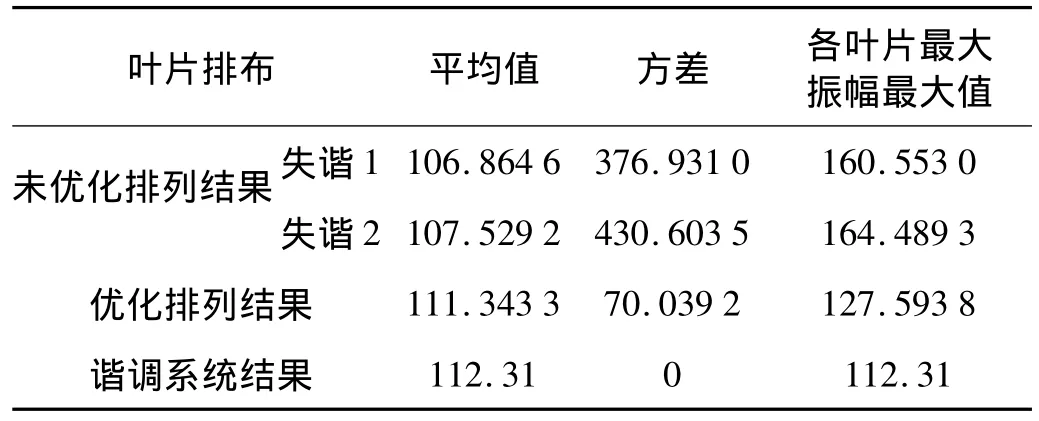
表4 各叶片排布叶盘系统振动情况比较Tab.4 Comparison of vibration condition under different blade arrangement

4 结论

本文通过分析发现对于一组既定的失谐叶片，其在轮盘上的安装排布顺序能很大程度上影响叶盘系统的振动情况，并提出通过人工蚁群算法对叶片安装排布顺序进行优化的方法。研究表明：选择适当的叶片排布顺序可以有效降低叶盘系统受迫振动幅值、减轻系统振动局部化程度，同时也证明本文所采用的方法可行、有效；通过叶片优化排列使失谐叶盘系统振动局部化程度有效减弱，但较谐调系统相比，仍存在局部化现象。研究结果对降低叶盘系统振动幅度、减轻系统振动局部化具有重要指导意义。

［1］Bendiksen O O. Localization phenomena instructural dynamics［J］.Chaos，Solitons and Fractals，2000，11：1621-1660.

［2］Wei S T，Pierre C.Localization phenomena in mistuned assemblies with cyclic symmetry part 1：free vibrations［J］.ASME Journal of Vibration，Acoustics，Stress and Reliability in Design，1988，110：429-438.

［3］李凤明，汪越胜，黄文虎，等.失谐周期结构中振动局部化问题的研究进展［J］.力学进展，2005，35（4）：498-512.

［4］Dye R C，Henry T A.Vibration amplitudes of compressor blades resulting from scatter in natural frequencies［J］.Journal of Engineering for Power，1969，91（3）：181-188.

［5］Ei-Bayoumy L E，Srinvasan A V.The effect of mistuning on rotor blade vibration［J］.AIAA Journal，1975，13：460-464.

［6］ Ewins D J.Vibration modes of mistuned bladed disks［J］.Journal of Engineering for Power，1976，98（7）：21-25.

［7］张 海，浦 健，张啸澄.基于退火单亲算法的压气机叶片排序［J］.燃气轮机技术，2009，22（4）：49-53.

［8］唐绍军，王 旭，朱 斌.遗传算法对压气机叶片排序的应用［J］.航空动力学报，2005，20（3）：518-522.

［9］杨 训，刑建华.基于遗传算法的转子叶片优化排列［J］.计算机仿真，2008，25（11）：94-97.

［10］赵德胜.多约束条件下基于改进遗传算法的叶片优化排序［J］.机械设计与制造，2010，12（9）：12-14.

［11］廖海涛，王建军，李其汉.随机失谐叶盘结构失谐特性分析［J］.航空动力学报，2010，25（1）：160-168.

［12］ Rahimi M，Ziaei-Rad S.Uncertainty treatment in forced response calculation of mistuned bladed disk ［J］.Mathematics and Computers in Simulation，2009，7（2）：1-12.

［13］袁惠群，杨少明，吴震宇，等.基于蚁群算法和模态局部化参数的失谐叶盘减振研究［J］.东北大学学报，2010，31（11）：1611-1614.

［14］王红建，贺尔铭.叶片失谐对叶盘结构振动特性的影响［J］.西北工业大学学报，2009，27（5）：645-650.

［15］詹士昌，徐 婕，吴 俊.蚁群算法中有关算法参数的最优选择［J］.科技通报，2003，19（5）：381-386.