基于贝叶斯网络的汽轮机组轴承工频振动诊断

黄海舟，纪 峰，袁小阳，朱 均

（1.西安交通大学 现代设计及转子轴承系统教育部重点实验室，西安 710049；2.湖北省电力试验研究院，武汉 430077）

研究设备运行状态在诊断信息中的反映是设备故障诊断的主要任务。然而，绝大多数设备故障诊断问题具有不确定性。因为，故障和征兆之间不完全存在一一对应关系，即一种故障可能表现出多种征兆，而一种征兆可能对应着多种故障，这就给设备故障诊断增加了难度。设备故障诊断方法可分为统计模式识别方法和结构模式识别方法两个大类，贝叶斯网络（Bayesian Network）诊断方法兼顾了这两类方法的优点。贝叶斯网络提供了一种不确定性推理的网络结构，最早由Pearl J提出并用于人工智能系统［1］。随后在设备诊断［2-3］、加工控制［4-5］和风险投资等领域得到广泛应用。以往采用贝叶斯网络诊断设备故障，主要利用振动的频域信息而其他重要信息流失，提出具有实质性应用价值的诊断网络也不多。本文针对汽轮机组轴承工频振动的诊断难点，提出了质朴型贝叶斯诊断网络，以最少的推理层面，融合振动的频谱、相位、趋势和运行工况条件等信息，实现对单一故障和复合故障的正确推理。诊断网络结构和条件概率赋值凝聚了大量现场经验和统计数据。

1 贝叶斯网络原理及推理计算

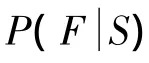
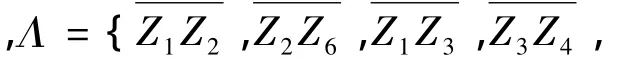
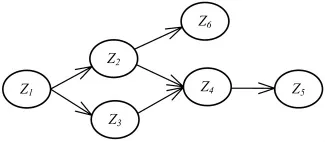
图1 简单贝叶斯网络Fig.1 A simple Bayesian network

贝叶斯网络推理计算，一般按照以下步骤进行：①根据领域专家知识或经验统计，给出各个假设（结论）的先验概率和条件概率；② 按分支分别计算各个联合概率分布；③ 计算各个节点的边缘概率；④ 进行统计推理，由贝叶斯公式计算不同组合情况下，假设（结论）成立的后验概率。

条件独立性和乘法定理是计算中的两个重要规则［6-7］。贝叶斯网络是单向网络，条件概率具有某种独立性（马氏性），即任一节点Zi发生的概率，仅依赖于该节点的直接双亲节点集Pa（Zi），而条件独立于由Zi的双亲节点给定的、非Zi后代节点构成的任何节点子集A（Zi）。乘法定理是由条件概率的定义得出的，指联合概率由条件概率组成的链乘公式得出。条件独立性使所需指定的条件概率的个数大大减少。

联合概率计算的一般公式为：

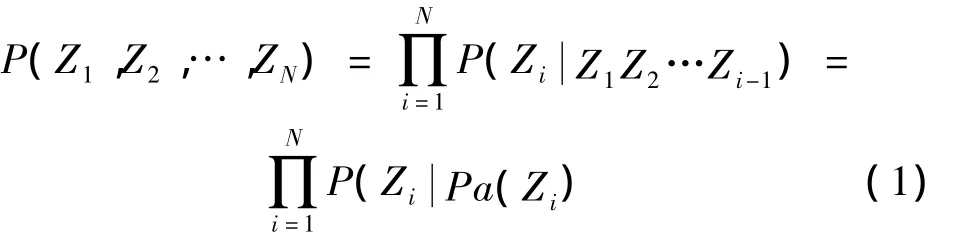
对图1有：

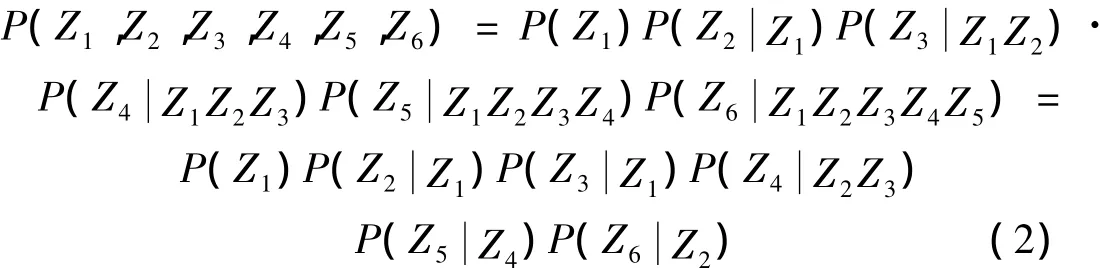
假如所有变量均为二值变量（0，1），则对6个变量求联合概率，理论上需要指定26=64个独立的条件概率值。而利用条件独立性，用式（2）计算，只需指定14个（2+2+2+4+2+2）条件概率值。所需指定的概率值的个数的减少，使得利用有限的领域专家知识或经验，计算在一定证据下假设成立的可信度成为可能。

全概率计算全概率即边缘概率，用于计算由事件联合概率求解其子事件边缘概率，遵守求和规则。

对图1，如Z1=true的概率计算可写为：

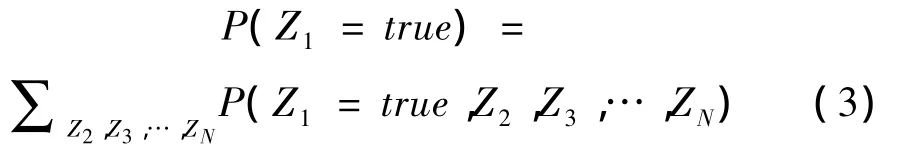
即先后对Z2，Z3，…，ZN进行求和操作。

贝叶斯公式假定有M个证据S1，S2，…，SM构成完备集，有M条规则S→F（LS，LF），给定N个假设的先验概率P（F1），P（F2），…，P（FN），则从假设先验概率求解其后验概率的贝叶斯公式公式为：

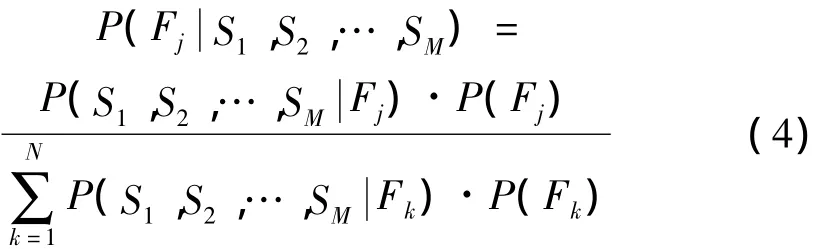
式中：j≤N。

2 贝叶斯网络用于汽轮机组轴承工频振动诊断

2.1 汽轮机组轴承转子系统振动故障的特征规律

不同类型旋转机械的振动故障表现征兆有一定差异。如汽轮发电机组与化工机械的振动故障表现是不太相同的，即使同类和同容量机械，由于结构等方面的差异振动特征可能很不一致。大容量机组许多振动征兆表现不同于小机组，甚至与某些文献提供的经典的“振动故障征兆表”［11］（以下简称“征兆表”）给出的征兆出现概率值不太一致。如大型汽轮机的摩擦振动，出现1X工频振动的概率，在“征兆表”中对应的概率为20%～30%，而实测的概率达到70%～80%，且大多数不包含显著的亚谐或超谐振动成分。又如，大型汽轮发电机组的转子不对中故障，“征兆表”中给出2X振动频率出现的概率为50%～60%，而实际大机组这一振动征兆表现并不多见，乃是以1X工频振动为主。此外，“征兆表”主要是根据振动的频率成分进行特征区分的，忽视了振动相位变化、振动随运行工况变化等重要信息。大型汽轮机组振动以1X工频振动占绝大多数，也是工程中最难诊断的振动问题。

2.2 轴承转子系统工频振动诊断网络设计

采用贝叶斯网络进行振动故障诊断，网络结构和众多先验概率值，只有针对特定类型机组设计时，才能保证其诊断功效及精度。文献［9］为石化机组设计了一种贝叶斯诊断网络，对振动故障根原因的排查提供了较高的智能化。文献［10］研究了具有三层事件的转子故障贝叶斯诊断网络。网络层数越多、先验概率赋值不精确，对推理计算精度影响会较大［11］，故本文采用国际流行的质朴型诊断网络。如图2为作者根据振动诊断经验提出的贝叶斯诊断网络，网络上列举了7种故障和9种征兆。与一般研究不同，在征兆层事件的设计上，除列入频谱特征外，把振幅和相位随运行工况变化、随时间变化及振动的方向性等均考虑在内；诊断网络中先验概率和条件概率值，来自作者近19年、280余台次机组的振动诊断统计数据和“征兆表”的部分数据。因此，计算推理更符合工程实际，诊断结果有较高的可信度。

理论上，任何一种故障与各个征兆都存在关联，只是关联度强弱而已。因而，从任何一种故障出发，向各个征兆都存在有向弧连接。例如，对7种故障和9种征兆，如每种事件均是二值变量，故障的先验概率赋值个数为2×7=14个，组合故障发生时出现相应征兆的条件概率赋值个数为9×27=1152个。因此，即便是两层贝叶斯网络，初始先验概率的赋值数量也很大，计算很复杂。贝叶斯网络实属NP难题。在实际诊断中，人们通常只关心一种故障发生时出现的最显著征兆或感兴趣的征兆，因而，故障和征兆之间的有向弧连接的数量可以大大减少，使计算简化。

2.3 诊断网络推理计算

网络先验概率及条件概率的赋值。网络中列出的7种故障是相互独立的，每种故障发生的先验概率，可认为是实际故障监测中统计求得的故障分布列数据，见表1。值得指出，不少资料给出转子不平衡故障占约70%，本文根据实际监测统计结果为纯粹不平衡问题约占40%；另外，由于工程中故障不限这7种，故所列7种故障先验概率之和小于1。

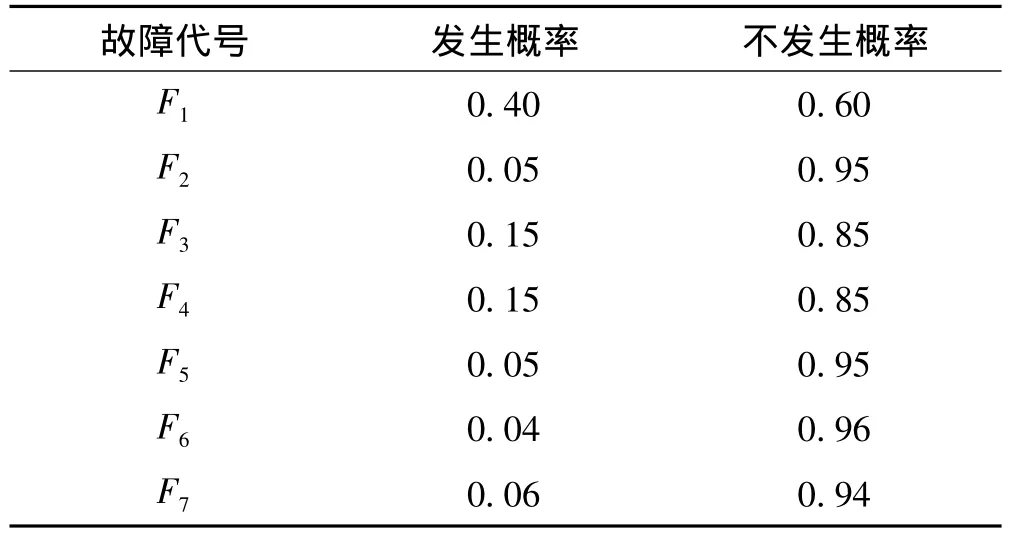
表1 故障先验概率赋值Tab.1 Failure prior probability assignment

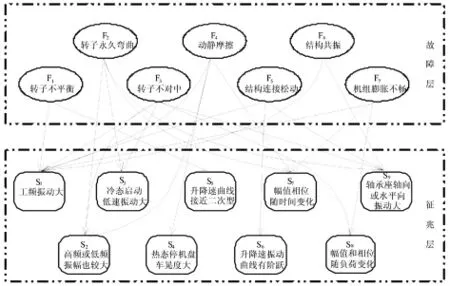
图2 汽轮机轴承工频振动故障质朴型贝叶斯诊断网络Fig.2 A nature Bayesian network for working frequency vibration diagnosis of turbine bearings

故障征兆层的条件概率赋值量较大，需要依据大量的试验统计数据。表2给出各条件概率值，它一部分基于试验统计，一部分取自“征兆表”。限于篇幅只列出了部分赋值。

征兆全概率的计算。根据式（3）计算征兆层各节点全概率。如计算P（S2），因F2、F3、F4相互独立，有：

征兆全概率计算结果也列入表2中。

故障诊断推理计算

故障推理直接按照式（4）的贝叶斯公式计算。本文在LabVIEW开发平台上编制了完整的计算程序，计算数据输入、输出方便，计算效率满足要求。

表2 条件概率赋值和全概率计算值Tab.2 Conditional probability assignment and total probability calculation

3 故障诊断案例

本文设计的诊断网路可适应于单一故障和复合故障的诊断推理。对于单一故障，征兆事件明显地支持某一种故障，称为简单证据。对于复合故障，故障可能由两种或两种以上原因引起，提供的证据集并不明显地支持某一种故障，称为复杂证据，这时，单一故障计算的概率值可能差别不大，而采用故障组合概率计算，可以判断各种复合故障发生的可能性的大小，这是比较符合实际情况的。

案例A：单一故障诊断推理计算

某双水内冷发电机#6轴承，轴承座水平方向振动相关特征如图3所示：波德图示出振动较严重超标，振幅降速大于升速，且升速工频振动有阶跃降-升特征；频谱图显示无论空载或大负荷，工频振动分量为特征分量并超标。故证据集SA归纳为征兆S1、S6和S9并存。

该证据发生的全概率为：

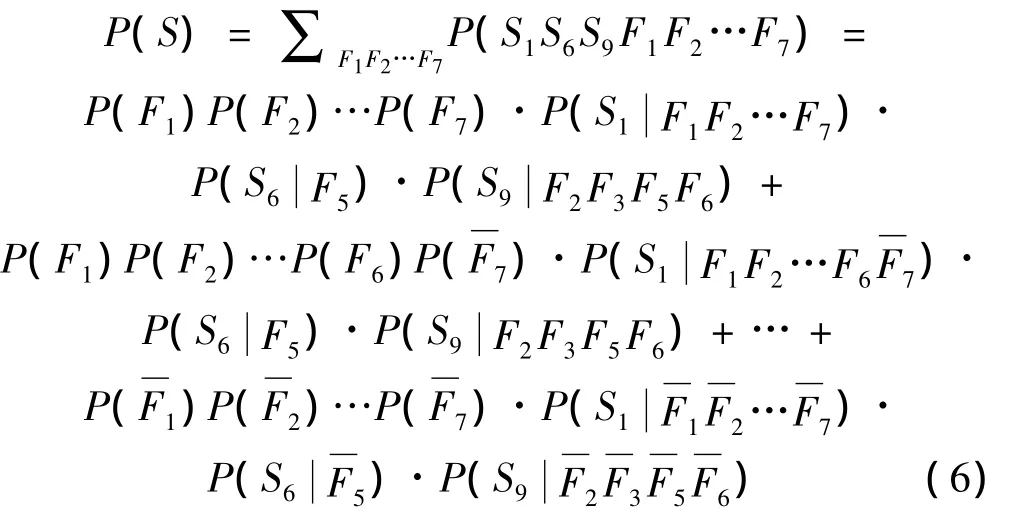
则单一故障发生的概率为：

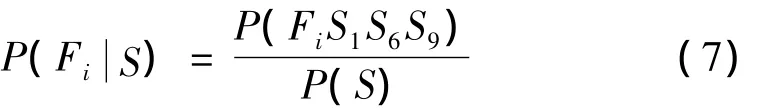
式（7）中，i=1，2，…，7。计算按如下步骤进行：

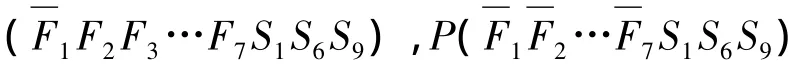
计算表明，发生“结构连接松动”单一故障的可能性最大。诊断计算结果与实际检查情况符合：现场检查发现#6轴承座台板联接螺栓因为多年运行发生松弛，台板与垫铁之间最大存在1.6 mm间隙，松动现象很隐蔽。打磨台板联接螺栓防松点焊并重新紧固后，振动故障消失。

案例B：复合故障诊断推理计算

某汽轮机#1轴承，轴承座水平方向振动相关特征如图4所示：从2.5 h带负荷过程振动瀑布图上可看出，振动除基频分量外，还存在一定高频和低频分量；从另一个6 h带负荷过程振动乃奎斯特图上发现，振幅随时间由小到大-由大到小变化，相位随时间逆转向旋转2.5周以上。此外，汽轮机转子在热态停机盘车之初晃动度较大，升降速振动变化曲线接近二次型。故证据集SB归纳为征兆S1、S2、S4、S5和S7并存。

推理计算过程如下：

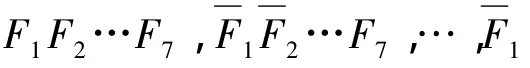
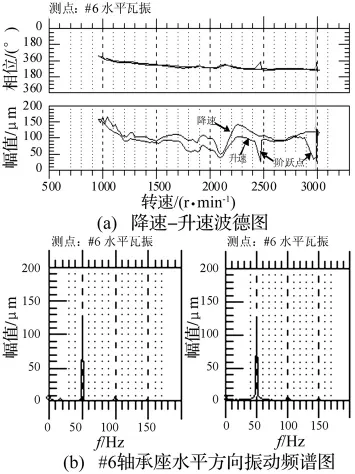
图3 证据集SA特征图Fig.3 Characteristic chart of symptom sets SA

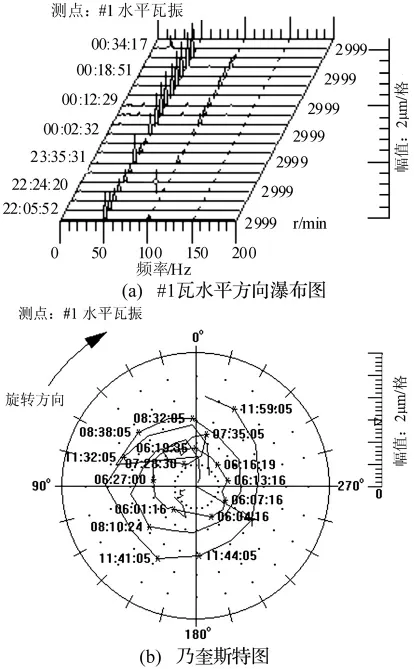
图4 证据集SB特征图Fig.4 Characteristic chart of symptom sets SB

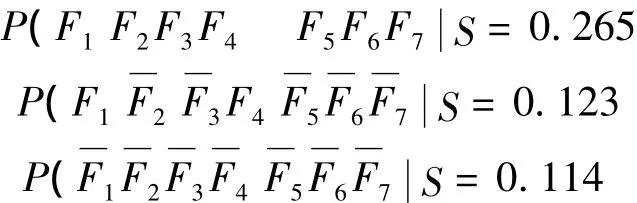
计算表明，同时存在“转子不平衡”和“动静摩擦”组合故障且无其它故障的概率，仅次于纯粹“转子不平衡“故障的概率，排在第3位的也是纯粹“动静摩擦”故障。故诊断计算结果认为同时存在“转子不平衡”和“动静摩擦”组合故障的可能性最大。诊断计算结果与实际检查情况符合：现场检查低压轴封套磨损深度接近10 mm。更换轴封套并采取现场动平衡减小轴系挠曲不平衡量后，振动故障消失。

4 结论

贝叶斯网络诊断机组轴承工频振动故障是可行的。对单一故障和复合故障，在质朴型贝叶斯网络中，用最少的推理层面，同时考虑振动频谱、相位、趋势和运行工况等诊断信息，可以提高实际诊断结果的准确性。

贝叶斯网络诊断机组振动或其他故障，要求赋值的先验概率数目较大，且最好针对具体机型。因此，贝叶斯网络方法在机组故障诊断领域的推广应用，取决于先验概率的完备程度。

［1］ Pearl J.Probabilistic reasoning in intelligent systems［M］.San Mateo，CA：Morgan Kaufmann，1988.

［2］Przytula K W，Thompson D.Construction of bayesian networks for diagnostics［C］.Proceedings of 2000 IEEE Aerospace Conference，2000，18-24.

［3］Yildiz B，Golay M，Maynard K P.Development of expert system with bayesian networks for application in nuclear power plants［C］. EPRI International Maintenance Conference，Houston TX，2001，14-16.

［4］Dey S，Stori J A.A bayesian network approach to root cause diagnosis of process variations［J］.International Journal of Machine Tools＆ Manufacture，2005，45：75-91.

［5］Wolbrecht E，Ambrosio B D，Passch B.Monitoring and diagnosis of a multi-stage manufacturing process using bayesian networks［J］.Artificial Intelligence for Engineering，Design and Manufacturing，2000，14（2）：53-67.

［6］ Lucas P J F.Bayesian model-based diagnosis［J］.International Journal of Approximate Reasoning.2001，27：99-119.

［7］盛 骤，谢式千，潘承毅.概率论与数理统计［M］.北京：高等教育出版社，1999.

［8］张正松，傅尚新，冯冠平，等.旋转机械振动监测及故障诊断［M］.北京：机械工业出版社，1991.

［9］胡兆勇，屈梁生.一种贝叶斯诊断网络的拓扑结构［J］.西安交通大学学报，2003，37（11）：1115-1118.

［10］徐宾刚，屈梁生.陶肖明.转子故障的贝叶斯诊断网络的研究［J］.机械工程学报，2004，40（1）：66-72.

［11］李俭川，胡茑庆，秦国军，等.贝叶斯网络理论及其在设备故障诊断中的应用［J］.中国机械工程，2003，14（10）：896-900.