一种考虑应变率效应的结构非线性时程分析方法

王文明，李宏男

（大连理工大学 建设工程学部，大连 116024）

土木工程中应用的大多数材料都有一定的率敏感性，钢筋混凝土结构是目前应用最为广泛的结构，钢筋和混凝土在不同应变率下有不同的力学性能。试验研究表明［1-6］，随着应变率的提高，钢筋和混凝土的特征强度有不同程度的提高。在地震作用下，混凝土的应变率一般能达到10-3～10-2/s，最大能达到10-1/s左右［3］，钢筋所能达到的应变率更大。对结构进行抗震分析时，采用静态下的理论不尽合理，应该考虑应变率效应。

对于一些复杂或者重要的抗震结构，需要对其进行弹塑性变形演算［7］。理论上说，振动台试验得到的结构响应最为可靠，但是这种方法无法普遍用于实际工程。非线性时程分析深受广大学者和工程师的认可，该方法目前被认为是相对精确的方法。然而到目前为止，该方法采用的本构关系、弯矩-曲率关系和破坏准则等大多都是在静力荷载作用下得到的。从数值计算的角度来说，通过该方法得到的结构响应是不精确的。为了提高该方法的准确性，在结构非线性时程分析中应该考虑应变率效应。国外一些学者对结构进行地震作用下的非线性时程分析时，考虑了应变率效应。研究表明，考虑应变率效应后，计算得到的结构响应发生一定的变化［8-9］。在有些情况下，变化很明显，这说明在非线性时程分析中考虑应变率效应是很有必要的。对结构进行非线性时程分析时，可以采用微观模型（如纤维模型），也可以采用宏观模型（如塑性铰模型）。对于宏观模型而言，计算过程中不计算某点的应力和应变，所以不可能精确地考虑应变率效应。对于微观模型，精确考虑应变率效应还存在一些困难。基于以上原因，本文提出了一种在结构非线性时程分（析中考虑应变率效应的近似方法，该方法不仅可以应用于微观模型，还可以用于宏观模型。文中给出了该方法的力学解释，并通过数值模拟对该方法进行了验证。

1 考虑应变率效应的非线性时程分析方法

在简谐运动中，回复力为零的位置叫做这个简谐运动的平衡位置。地震作用下，结构发生复杂的往复运动，各层间剪力为零的位置为结构的平衡位置。材料没有进入非线性阶段之前，结构的平衡位置为结构的初始位置。如果材料能够进入非线性阶段，由于残余位移的存在，结构的平衡位置会发生变化。在地震作用下的很多时刻，结构的基底剪力为零。可以近似认为，当结构的基底剪力为零时，结构处在平衡位置。本文将相邻的平衡位置出现时刻之间的过程称为一个半循环，如图1所示（图1为文中模型在峰值加速度调幅到6 m/s2的El Centro波作用下的顶点位移时程曲线，取前5 s）。在地震作用过程中，结构的顶点位移有很多极值点。在绝大多数情况下，结构的顶点位移在一个半循环内仅有一个极值。本文将相邻的平衡位置和顶点位移极值所在时刻之间的过程称为一个1/4循环。一个半循环可以分为两个1/4循环，分别称为前1/4循环和后1/4循环。

图1 顶点位移时程曲线Fig.1 Time history of top displacement

本文提出的考虑应变率效应结构非线性时程分析方法的具体步骤如下：

（1）建立结构力学模型，对结构进行不考虑应变率效应的非线性时程分析。

（2）对模型的设置进行修正。修正步骤如下：确定顶点位移达到最大值的时刻和之前结构处在平衡位置的时刻（即基底剪力为零的时刻），计算该1/4循环的时间；分别计算这两时刻进入非线性构件控制截面各处钢筋和受压区边缘位置的应变，然后计算这些位置在该1/4循环内应变的变化量；将应变变化量除以该1/4循环的时间，得到这些位置在该1/4循环内的平均应变率；根据各处钢筋的平均应变率修改相应位置钢筋的本构关系，根据受压区边缘位置平均应变率的2/3修改混凝土的的本构关系。

（3）对结构进行第二次非线性时程分析。

下面对为什么进行两次分析进行解释。第一次分析没有考虑材料的应变率效应，计算结果不可靠，第二次分析是第一次分析的修正。不进行多次分析的原因如下：① 该方法是一种实用方法，进行多次分析会大大降低该方法的实用性；② 第三次和第二次的分析结果相差很小，可以忽略不计。

2 方法的力学解释和意义

2.1 方法的力学解释

该方法的力学解释如下：

（1）对于结构来说，在地震作用下，存在一个或者几个对其有重要影响的1/4循环，其中最大变形对应的前1/4循环尤为重要。如果在该1/4循环内采用的本构关系更为合理一些，计算得到的结构反应能更为准确一些。

（2）在1/4循环内，如果材料必须采用某固定应变率下的本构关系，采用平均应变率下的本构关系是较为合理的。

（3）根据控制截面一些位置的平均应变率对整个构件的本构关系进行修正是合理的。在地震作用下，构件的非线性变形集中于局部，其他部位保持弹性。对于处于弹性阶段的部位，不管采用多大应变率下的本构关系，都不会对计算得到的结构响应产生影响（在不同的应变率下，可以认为材料的弹性模量和泊松比不变）。

（4）材料的动态强度提高幅度与应变率的对数近似成线性关系［1-6］。这意味着只有当应变率发生量级的变化时，材料的屈服强度才产生较为明显的变化。以HRB335钢筋为例，应变率为0.1/s时，屈服强度为387.93 MPa；应变率为 0.2/s时，屈服强度为 394.03 MPa（应变率之比为2，屈服强度之比为1.016）。在地震作用下，对结构有重要影响的1/4循环可能有多个。在这些不同的1/4循环内，任意一点平均应变率的比值一般在0.5～2之间。这意味着，对结构进行第二次非线性时程分析时，材料的本构关系在对结构有重要影响的时间段内是合理的。

（5）在地震作用的很多时间段内，结构不产生塑性变形。在这些时间段内，不管采用多大应变率下的本构关系，都不会对计算得到的结构响应产生影响。

基于以上原因，可以看出本文提出的方法是合理的，下文会通过数值模拟的方法对其进行进一步验证。

2.2 方法的意义

对结构进行非线性动力时程分析时，可以采用微观模型，也可以采用宏观模型。微观模型是指，在计算过程中需要计算结构中某点的应力和应变的模型，如纤维模型；宏观模型是指，在计算过程中不计算任意一点的应力和应变的模型，如塑性铰模型。一般来说，采用微观模型对结构进行分析，计算结果更为可靠，但是计算成本较高。有鉴于此，本文方法的意义如下：

（1）本文方法对微观模型具有一定意义。理论上说，对结构进行非线性时程分析时，如果采用微观模型，可以采用材料的动态本构模型（能够精确考虑应变率的不断变化）。然而，目前为止，在分析中采用材料的动态本构模型还存在一些应用上的困难。目前，绝大多数软件没有这项功能。ABAQUS虽然拥有这项功能，但是软件中只有CDP（Concrete Damaged Plasticity）模型适用于混凝土结构的抗震分析，这种材料模型不能用于B31单元，用于B21单元时不能考虑应变率效应。对于钢筋混凝土框架结构而言，如果计算时采用动态本构模型，梁和柱只能采用实体单元，然而实体单元难以应用于工程实际。除此之外，混凝土采用CDP模型时，如果考虑应变率效应，计算难以收敛。可以说，用微观模型对结构进行分析时，本文提出的方法具有一定意义。

（2）本文方法对宏观模型具有重要意义。用宏观模型进行非线性动力时程分析时，计算过程中不计算任意一点的应力和应变。这意味着，对于宏观模型而言，无法精确地考虑材料的应变率效应。如果在宏观模型中考虑应变率效应，必须采用近似方法。这里提出的方法可以用于宏观模型。

下面简要说明一下如何在塑性铰模型中使用本文方法。设置塑性铰时，需要确定塑性铰的骨架曲线和滞回规则。骨架曲线可以是弯矩和曲率的关系，也可以是弯矩和转角的关系。按照本文的方法，需要在步骤2中对模型的设置进行修正。方法如下：首先，确定进入塑性的塑性铰截面曲率为屈服曲率和极限曲率时截面各处钢筋和受压区边缘的应变（第一次分析之前即可确定）；其次，计算这些截面在顶点位移达到最大值时刻和之前基底剪力为零时刻的曲率，采用线性插值的方法分别计算各处钢筋和受压区边缘在这两个时刻的应变，进而求得这些点在该1/4循环内的平均应变率；最后，根据这些点的平均应变率对相应塑性铰的设置进行修正（修正骨架曲线）。

下面以屈服弯矩为例说明骨架曲线的修正方法。采用塑性铰模型时，一般不考虑混凝土的抗拉强度。对于钢筋混凝土矩形截面柱，截面屈服弯矩可按下式计算［10］：

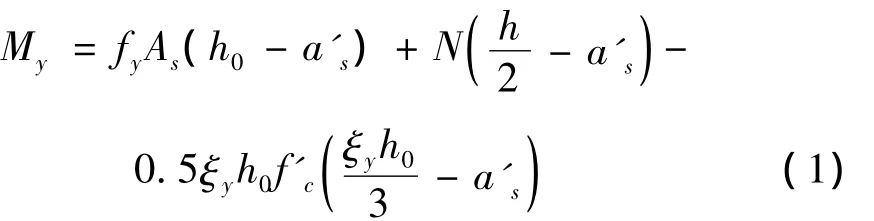
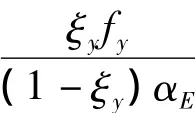
计算截面的动态屈服弯矩时，钢筋的屈服强度采用动态屈服强度，式中与fy有关参数（ξy和f'c）的计算均需采用钢筋的动态屈服强度。

3 方法的验证

相对来说，如果在非线性时程分析时采用的本构关系为动态本构模型，那么计算的结构反应可以被认为是精确解。如果按照本文方法计算的结构反应十分接近精确解，即可验证本文方法是有效的。

3.1 采用的动态本构模型

试验研究表明，随着应变率的提高，钢筋的弹性模量基本不变，钢筋的屈服强度和抗拉强度都有一定程度的提高，强度低的钢筋比强度高的钢筋对应变率更为敏感［1-2］。在地震作用下，钢筋的应变率一般不会超过1/s，其动态本构模型可以按照作者在文献［2］中给出的模型选取，即：

随着应变率的提高，混凝土的弹性模量和泊松比如何变化没有达成一致共识［4］，这里不考虑混凝土弹性模量和泊松比随应变率的变化。随着应变率的提高，混凝土的抗压强度有明显的增加趋势。混凝土动态抗压强度可按下面的公式计算［5］：

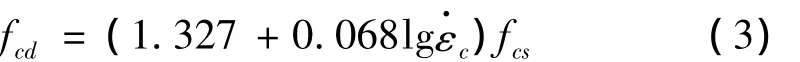
式中：fcd为当前应变率下的抗压强度；fcs为准静态应变率下的抗压强度；c为当前的应变率。

随着应变率的提高，混凝土的抗拉强度有明显的增加趋势。混凝土动态抗拉强度可按下面的公式计算［6］：

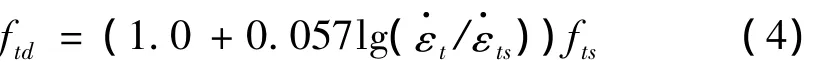
式中：ftd为当前应变率下的抗拉强度t为当前的应变率；ts为准静态应变率，这里取为ts=10-5/s；fts为准静态应变率下的抗拉强度。

3.2 模型介绍

采用的结构模型如图2所示，该结构由一根无质量的钢筋混凝土柱和柱顶的质量块组成。质量块质量为4 800 kg，沿柱全长配置φ8@100的箍筋。

纵筋采用HRB335，箍筋采用HPB235，弹性模量分别为2.0×1011Pa和2.1×1011Pa，钢筋采用理想弹塑性本构模型，纵筋在不同应变率下的本构关系如图3所示（应力σ和塑性应变εin的关系，应力单位为Pa）。通过定义一系列不同塑性应变率下屈服强度比的方法生成钢筋的动态本构模型，软件在计算的过程中根据线性插值的方法计算每一时刻每一积分点的应力和应变。混凝土强度为 C30，采用 CDP模型［11］，混凝土在不同应变率下的本构关系如图4所示（应力σ和塑性应变 εin的关系，应力单位为Pa），通过定义一系列塑性应变率下混凝土的本构关系的方法生成材料的动态本构模型。混凝土柱采用C3D8R单元，单元大小为0.1 m ×0.1 m ×0.1 m，钢筋采用 T3D2单元，单元长度为0.1 m，通过软件中的Embedded将钢筋埋入混凝土之中，不考虑钢筋与混凝土之间的粘结滑移。

图2 结构模型（mm）Fig.2 The model

图3 钢筋的本构关系Fig.3 The constitutive relationship of rebar

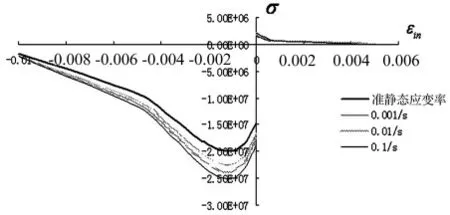
图4 混凝土的本构关系Fig.4 The constitutive relationship of concrete

3.3 地震波的选取

计算中，采用三条地震波，分别为El Centro波、Northbridge波和 Taft波，峰值加速度分别调幅到8 m/s2、8 m/s2和 6 m/s2，三条地震波均取前 15 s进行输入。

3.4 分析工况设置

每次分析时，均设置两个分析步。首先是静态分析，然后是动态分析。其中静态分析用于自重作用分析，动态分析用于地震作用分析。需要说明的是，对结构进行自重作用分析时，如果材料采用的是动态本构模型，应变率在分析过程中起作用。这是由于在ABAQUS软件中，不论是静态分析还是动态分析，均需要设置分析总时间，分析中应变随时间变化，应变率就起作用。自重作用分析时，不应该考虑应变率效应，这可以通过调大静态分析总时间的方法消除应变率效应对自重分析的影响。当然，如果材料在自重作用下不能进入非线性阶段（应变率不起作用），就可不必注意此问题。

按照5%的阻尼比设置材料的阻尼参数，由于文中模型可以看成单自由度体系，设置材料的阻尼参数时，仅需计算Alpha，Beta等于零。对结构进行地震作用分析时，均采用隐式算法。

3.5 分析结果

结构在三条地震波作用下的最大反应如表1所示。为了便于在整个时程内比较不同计算方法得到的结构响应，这里给出了一些主要的时程曲线。应变最大的纵向钢筋单元在El Centro波作用下的应力时程和应变时程分别如图5和图6所示，结构在三条地震波作用下的顶点位移时程分别如图7、图8和图9所示。

通过对计算结果进行分析，可以得到以下结论：

（1）采用动态本构模型得到的单元应变时程和应力时程与采用静态本构模型得到的结果有明显的不同。在ElCentro波作用下，采用动态本构模型时，纵向钢筋的最大应力为388.6 MPa，大约是其静力屈服强度的1.16 倍。

（2）材料没有进入非线性阶段之前，各种方法计算得到的结构响应时程相同；材料进入非线性阶段之后，各种方法计算得到的结构响应时程不同，但是曲线形状相似。

（3）采用静态本构计算得到的结构最大反应具有较大的误差。在所有的分析工况中，采用静态本构计算得到的结构最大反应相对误差的绝对值均大于5%。最大顶点位移的相对误差更为明显，最大为16.27%。可以看出，在非线性时程分析中考虑材料的应变率效应是很有必要的。

（4）本文方法的精度较高。采用本文方法计算得到的结构最大反应具有较小的误差，相对误差的绝对值均没有超过5%。在El Centro波和Taft波作用下，按照本文方法计算得到的结构顶点位移时程与精确解几乎重合，这说明本文提出的方法精度较高。

表1 结构的最大反应Tab.1 The maximum response of the structure

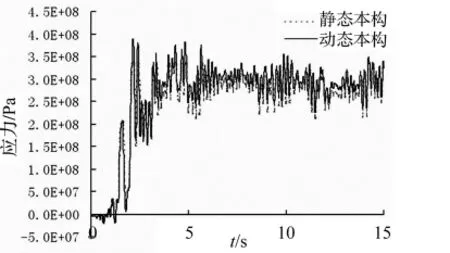
图5 某钢筋单元在El Centro波作用下的应力时程Fig.5 Stress history of a rebar element under El Centro ground motion

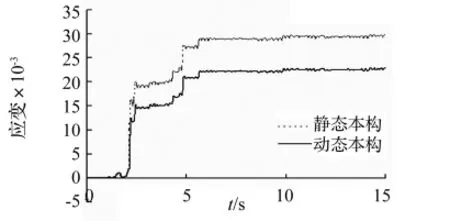
图6 某钢筋单元在El Centro波作用下的应变时程Fig.6 Strain history of a rebar element under El Centro ground motion

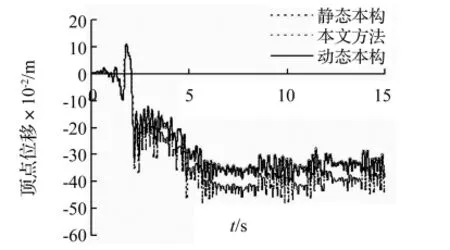
图7 结构在El Centro波作用下的顶点位移时程Fig.7 Top displacement history of the structure under El Centro ground motion

4 结论

本文提出了一种在结构非线性动力分析中考虑应变率效应的近似方法，该方法可以用于微观模型和宏观模型。文中给出了该方法的力学解释，并通过数值模拟对该方法进行了验证。结果显示，本文提出的方法具有较高的精度，可以作为一种在非线性时程分析中考虑应变率效应的有效方法。

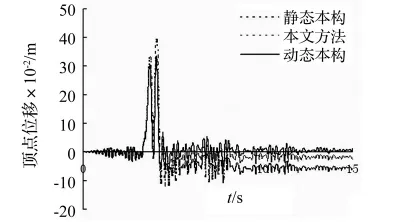
图8 结构在Northbridge波作用下的顶点位移时程Fig.8 Top displacement history of the structure under Northbridge ground motion

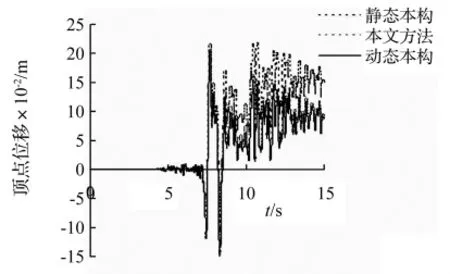
图9 结构在Taft波作用下的顶点位移时程Fig.9 Top displacement history of the structure under Taft ground motion

［1］林 峰，顾祥林，匡昕昕，等.高应变率下建筑钢筋的本构模型［J］.建筑材料学报，2008，11（1）：14-20 .

［2］李 敏，李宏男.建筑钢筋动态试验及本构模型［J］.土木工程学报，2008，43（4）：70-75.

［3］Bischoff P H，Perry S H.Compressive behavior of concrete at high strain rates［J］.Materials and Structures，1991，24（6）：425-440.

［4］闫东明.混凝土动态力学性能试验与理论研究［D］.大连：大连理工大学，2006.

［5］董毓利，谢和平，赵 鹏.不同应变率下混凝土受压全过程的实验研究及其本构模型［J］.水力学报，1997（7）：72-77.

［6］肖诗云，林 皋，王 哲，等.应变率对混凝土抗拉特性的影响［J］.大连理工大学学报，2001，41（6）：721-725.

［7］GB 50011-2001.建筑抗震设计规范［S］.北京：中国建筑工业出版社，2001.

［8］Pankaj P，Lin E.Material modelling in the seismic response analysis for the design of RC framed structures［J］.Engineering Structures，2005，27（7）：1014-1023.

［9］Bhowmick A K，Driver R G，Grondin G Y.Seismic analysis of steel plate shear walls considering strain rate and P-delta effects［J］.Journal of Constructional Steel Research，2009，65（5）：1149-1159.

［10］赵国藩.高等钢筋混凝土结构学［M］.北京：机械工业出版社，2005.

［11］ ABAQUS Inc.ABAQUS analysis user’s manual［M］.American：ABAQUS INC.，2008.