结构化流道近壁区软性磨粒流流动仿真及实验研究

计时鸣，唐 波，谭大鹏，李 军，翁晓星，晓风清

(浙江工业大学 特种装备制造与先进加工技术教育部/浙江省重点实验室，杭州 310014)

模具行腔表面的复杂性和无规则性，给精密模具微细结构部件制造带来极大的困难和挑战。在模具制造过程中，为了消除模具表面所残留的机械加工痕迹，光整加工技术成为必要的工艺环节，占整个模具制造时间的50%以上。现有方法一般需借助工具接触或靠近待加工表面进行加工［1-2］。在光学元件加工领域，将凹槽、棱柱、棱镜阵列等立体结构的表面称为结构化表面［3-4］，借此也将模具中沟、槽、孔、棱柱、棱锥、窄缝等复杂异型面统一称为结构化表面。基于工具接触加工机理的光整加工方法难以应用于模具结构化表面的精密加工，因此，模具结构化表面的精密加工成为亟待解决的技术难题，文献［5］提出了一种基于软性磨粒流的模具结构化表面无工具精密光整加工新方法。

由于流体磨料的流动性，特别适用于加工异形曲面、窄缝和小孔等常规方法难以加工的表面。磨粒流加工可用于航空、汽车、模具、液压和医疗等行业［6］。磨粒流加工工艺能提供高质量的加工表面和获得闭合型公差［7］。松散磨粒与液体混合，可构成液固两相软性磨粒流(即弱黏性或无黏性液固两相磨粒流)，磨粒流的流体性质决定其可变化无形且无孔不入。因此，基于软性磨粒流形成了一些表面加工方法，由于软性磨粒流可形成良好仿形接触，因而在曲面和异型面加工中体现出优势［8］。

随着计算机功能的飞速发展，运用计算流体力学(Computational Fluid Dynamics，CFD)技术对包含有流体流动和热传导等相关物理现象的系统所做的分析［9］。为了准确地模拟近壁区软性磨粒流的流场，在壁面区域采用了双层模型和增强壁面函数相结合的方法，在流体控制方程里引入反映湍流效应的相关项，从而实现对湍流的模拟。为了揭示模具结构化表面近壁区软性磨粒流的压力场及速度场的分布规律，有效预测其软性磨粒流的材料去除特性，本文用FLUENT-6.3.26软件对软性磨粒流的流动进行模拟，用流体体积(Volume of Fluid，VOF)模型和重整化群(Renormalization Group，RNG)k-ε湍流模型，通过对结构化流道的结构进行合理的网格划分和特殊边界条件设置，对结构化流道内部的软性磨粒流流动进行数值模拟。

1 软性磨粒流加工原理

所谓的软性磨粒流，指的是具有弱黏性或无黏性的液固两相磨粒流，与具有强黏性的硬性磨粒流相比，具有更好的流动特性可实现湍流流动。为了利用软性磨粒流对尺寸小且结构特殊的结构化表面(沟、槽、窄缝等)的光整加工，需要软性磨粒流以一定压力和流速在结构化表面形成湍流流态，因此须引入约束模块与结构化表面组合，以构成一个封闭的结构化流道。高速流动的软性磨粒流在特定的流道截面形状约束下，形成湍流流动，对作为结构化流道内壁面一部分的结构化表面进行冲蚀微切削，实现精密光整加工。对不同形态的模具结构化表面，可以设计不同形状的约束模块，形成不同截面形状的结构化流道。

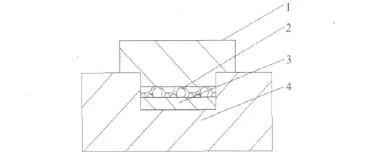
图1 模具结构化表面与约束模块Fig.1 Schematic diagram of between the mould structural flow and restrain module

模具结构化表面与约束模块的示意图如图1所示，试件3放在夹具4上表面，约束模块1和夹具4通过夹紧装置将其相互紧固，试件3与约束模块1形成一定间隙的结构化流道2，夹具4的表面与约束模块1之间视需要布置密封垫，以防止加工过程中软性磨粒流的泄漏，结构化流道2的厚度可以根据试件3与夹具4的接触面间添加细薄工件进行调整。

采用软性磨粒流加工的主要优点在于:可以使软性磨粒流与复杂形状的模具结构化表面形成良好接触，克服了细小尺度的结构化表面无法使用工具进行光整加工的困难;利用软性磨粒流的湍流壁面效应实现表面的微力微量切削，不会导致结构化表面的机械变形;软性磨粒流在流道内的单向循环流动提高了磨粒流的利用率和加工效率，并可有效过滤加工残留物及减少排放污染;加工过程可自动化进行。

2 RNG k－ε紊流模型

为更加精确地模拟应变大和流线弯曲度大的流动问题，Yakhot等［10］将RNG方法引入到紊流研究中，建立一个新的紊流模型(重组化群紊动动能-紊动耗散率紊流模型)。该模型是针对充分发展的湍流流动区域，通过瞬时的Navier-Stokes方程用RNG的数学方法推导出来的。在RNGk-ε模型中，通过大尺度运动和修正后的粘度项体现小尺度的影响，在控制方程中系统地去除了小尺度运动。RNGk-ε双方程紊流模型的连续方程、动量方程和湍动能k与耗散率ε方程可以表示成如下形式。

连续方程:

式中:t为时间，单位s;ux、uy为x、y方向磨粒流速度，单位为m/s;ρ为磨粒流密度，单位kg/m3。

动量方程:

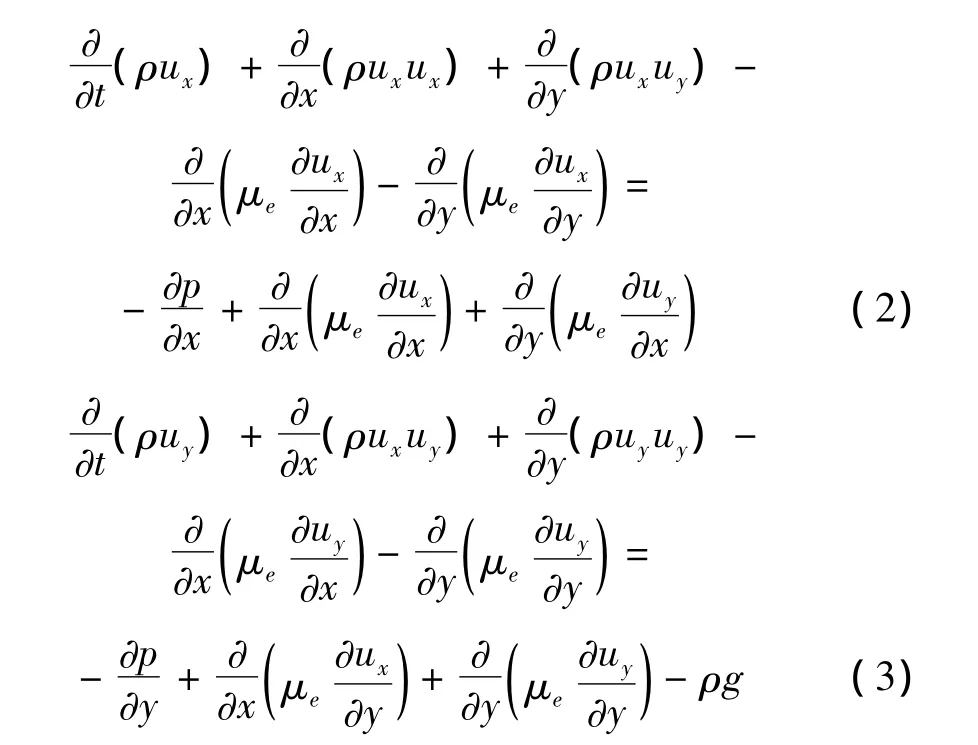
式中:p为压力，单位Pa;g为重力加速度，单位m/s2;μe=μ+μt，μ 为分子动力黏性系数，μt=ρCμk2/ε 为紊动黏性系数，其中Cμ=0.084 5。

湍动能k方程:

式中:k为紊动动能，σk=0.717 9。

耗散率ε方程:

式中:ε为耗散率，σε=0.717 9，

3 液－气两相流的VOF模型

VOF模型是一种在固定的欧拉网格下的表面跟踪方法，当需要得到一种或多种互不相溶流体间的交界面时，可以采用这种模型。VOF方法除提高自由面的模拟精度外，其处理的边界条件越来越复杂，适用范围越来越广，所解决的问题涉及化学、热能、机械、水利等众多学科和不同领域，在未来应用中将有更广阔的前景。引入VOF方法的RNGk-ε紊流模型方程形式与单相流的RNGk-ε紊流模型方程(1)～(5)完全相同，只是属性ρ和黏性系数μ的具体表达式不同，这两个参数是由计算单元中的相体积分数给出的，可以表示成如下的方程表达式:

式中:(1-α2)和α2分别表示软性磨粒流的体积分数，ρ1和ρ2分别为软性磨粒流和空气的密度，μ1和μ2分别为软性磨粒流和空气的分子动力黏性系数。

将方程(6)～(7)与RNGk-ε紊流模型基本方程(1)～(5)联立求解，就可以得到各未知变量，如压力、速度、紊动动能、紊动耗散率以及软性磨粒流体积率函数的分布。

4 材料去除的数学模型

在Preston方程中，将速度和压力以外的一切因素的作用全部归为一个比例常数k，即可建立材料去除率、压力和瞬时速度的线型关系:

式中:dz/dt表示软性磨粒流被加工模具工件材料的去除率;K是Preston常数［11］，其中K1为被抛光材料对工件材料去除率的影响系数、K2为磨粒的材料对工件材料去除率的影响系数、K3磨粒颗粒的形状对工件材料去除率的影响系数、K4为磨粒的大小对工件材料去除率的影响系数、K5软性磨粒流的配比对工件材料去除率的影响系数、K6为软性磨粒流的抛光温度对工件材料去除率的影响系数、K7为其他因素对材料去除率的影响系数。P(x，y，t)为模具工件表面受到的软性磨粒流的压力;V(x，y，t)为软性磨粒流的速度与被加工模具工件的相对速度。

定义去除函数Z(x，y，t)为软性磨粒流加工的结构化流道中模具工件被加工表面在时间T内的平均材料去除量，即:

式中Z(x，y，t)为时间T内的材料去除量。T为软性磨粒流流过结构化流道中模具工件被加工表面的时间。

5 数值模拟和边界条件

5.1 数值算法和边界条件

随着计算机功能的飞速发展，CFD已成为解决各种流体流动的强有力辅助工具，而由美国FLUENT公司推出的CFD计算软件以其功能全面、适用性广等优点，广泛应用于国内外的众多科研单位。本文在计算过程中对控制方程和边界条件使用有限体积法进行离散，压力方程采用PRESTO格式，体积分数方程采Georeconstruct格式，动能、湍动能、湍流耗散率方程的离散格式采用二阶迎风差分格式，并使用压力隐式算子分割(Pressure Implicit With Splitting of Operators，PISO)算法［12］求解压力-速度耦合，PISO算法是基于校正压力与速度之间的高度近似关系的一种算法，尤其适用于瞬态问题且可减少计算高度扭曲网格所遇到的收敛性困难。流场瞬态迭代计算时的收敛标准为10-3。每个方程都达到收敛标准后，再进行下一步迭代。

相关数值计算条件描述如下:入口边界条件为速度入口，出口边界条件为自由出口，为了达到采用近壁面的目的以及靠近壁面网格保证标准双层模型方法的精确度，采用了双层模型和增强壁面函数相结合的方法，壁面边界采用黏性无滑移条件，并假定没有质量交换。软性磨粒流的密度为0.88×103kg/m3、运动粘度为4.6×10-7m2/s，磨粒(金刚砂)与流体(46号机械润滑油)体积比为1:9。流体产生湍流的基本条件为雷诺数达到临界值(一般流道雷诺数Re＜2 000为层流状态，Re＞4 000为湍流状态，Re=2 000～4 000为过渡状态)，不同的入口速度对应的雷诺数如表1所示，表中的雷诺数均超过了湍流状态的雷诺数，可以认为流道中的软性磨粒流达到了湍流流动的状态。

表1 仿真模型初始参数Tab.1 Initial parameters in simulation

5.2 几何模型和网格划分

约束模块中的流道结构具有对称性，本文以中心截面作为研究对象，由于流道结构简单，单精度求解器就能很好地满足计算精度要求，故在计算过程中采用了单精度非稳态隐式分离求解器进行求解，流道结构尺寸具体如图2所示(单位:mm)。网格生成技术是计算机流体力学的重要内容，网格划分方式、疏密和数量都会对计算精度和计算规模产生直接影响，因此，有必要对网格生成方式给予足够的关注。计算区域和网格划分由GAMBIT-2.2.30前处理器生成，采用了三角形单元的映射成结构化网格，出入口位置对称与不对称网格划分图分别如图3、图4所示。

6 数值模拟结果与分析

在Preston方程中，等式右边除了常数K之外就跟压力和速度两个参数有关，流场中的压力分布和速度分布，应该被合理地视为两种被赋予独立物理内涵的独立物理量。因此研究流道中的压力和速度的关系和规律就显得有意义。

6.1 出入口位置对称时的压力、速度分布

在不同入口条件下，流道中软性磨粒流的压力云图和速度云图分别如图5、图6所示，图中(a)、(b)、(c)、(d)、(e)分别表示入口速度为 70 m/s，80 m/s，90 m/s，100 m/s，110 m/s。

图5 结构化流道压力分布云图Fig.5 Pressure distribution diagram of structural flow

图6 结构化流道速度矢量分布图Fig.6 Velocity vector distribution diagram of structural flow

从图5中看出:在同一个轴向截面上压力分布不均匀，且呈非线性分布，其中靠近入口和出口区域处，压力的变化比较明显;在入口区域段，软性磨粒流经缓冲后由上方流过被加工的工件表面，由于入口位置在加工工件的下方，软性磨粒流对入口处有较强的冲击，加工区域的上方压力比下方大，这对上方的约束模块磨损较大，对下方被加工工件表面的加工效率的提高不利;随着入口速度的增加，加工区域流道中的压力也随之增加，流道中轴向压力的增加幅度大于其径向压力的增加幅度，这有利于软性磨粒流快速的流过工件表面，提高软性磨粒流的切削能力，从而提高工件的加工效率。从图6中可看出:随着入口速度的增加，流道中速度的流动更加无规律性，这正是湍流状态的表现形式，软性磨粒流在加工区域中可以反复碰撞被加工表面，有效提高了加工效率;在入口缓冲区域和出口区域，由于结构的不规则性和复杂性，对进口和出口的冲击很大，并且在出入口附近存在一些小漩涡，对加工区域中工件的表面会产生一定的影响;加工区域中，不同位置的径向、轴向速度是不一致的，软性磨粒流在加工区域的入口段，流道上方的速度比下方的速度大，加工区域的中间段变化较平缓，在加工区域的出口段，流道的下方速度有所增大，呈现中间大，上下两边小的分布情况。

6.2 出入口位置不对称时近壁区压力和速度分布

为了研究工件表面近壁区软性磨粒流对工件表面的作用特性，本文通过采样流道加工区域工件上方0.2 mm、0.35 mm、0.5 mm 处的轴向压力、速度若干数据点来探讨加工区域轴向长度上压力、速度的分布变化情况，并预测材料的去除率。轴向长度与压力、速度的关系图分别如图7和8所示。从图中可以看出，在加工区域的入口段和出口段，压力和速度有明显的波动情况，在加工区域的入口5 mm处速度和压力达到最大值，在加工区域的中间段，沿着轴向位置压力逐渐下降，快到出口处压力降到最低;在加工区域的不同径向位置，压力和速度分布也不一样，越靠近壁面，受到的阻碍就越大，压力和速度值也就越小。

可以依据式(8)～式(9)Preston基本式，得到图9所示的工件表面近壁处轴向长度与材料的去除率关系图，由于同一配方软性磨粒流的去除率方程中的K值在流道的不同位置均相等且为常值。从图9中可以发现:随着软性磨粒流的向前运动，材料去除率也随之发生变化，在入口处附近材料去除率达到最大值，后逐渐变小。因此为了避免软性磨粒流冲击工件表面，在软性磨粒流流经工件表面之前，加入一个引流模块，其长度要超过软性磨粒流去除率达到最大值所对应的位置。

6.3 出入口位置对称和不对称的压力速度比较

取一组速度入口条件下，流道中压力速度的分布情况。当入口速度为110 m/s时，出入口对称与不对称流道中的压力和速度统计图分别如图10～图11和图12～图13所示，从图中可以看出:软性磨粒流的入口位置不同时，流道中的压力、速度分布也随之发生变化，软性磨粒流的压力、速度最大、最小值也发生变化;出入口对称时压力为0～107Pa区间比例最高，约为58%，压力超过8×107Pa区域所在的比例非常小，不超过10%;出入口对称时速度在100～150 m/s区间的比例约为25%，速度值为0～150 m/s所占的比例57%。出入口不对称时压力为0～107Pa区域比例也为最高，约为61%，压力超过8×107Pa区域所在的比例非常的小，不超过5%;出入口不对称时速度在100～150 m/s区间的比例约为30%，0～150 m/s所占的比例56%，该比例与入口对称时基本接近。

7 加工试验验证

本文搭建软性磨粒流精密加工试验平台，原理简图如图14所示。软性磨粒流精密加工试验平台原理简图。平台主要由控制柜、磨粒流搅拌器、隔膜泵、高速摄像机和辅助检测器等四大部分及一整套管路阀门及附属部件组成。软性磨粒流存储在溶液箱中，通过隔膜泵驱动对待加工试件进行加工，然后通过管道返回溶液箱。

图14 软性磨粒流精加工试验平台Fig.14 The trial platform of softness abrasive finishing machining

图15 加工前后工件局部表面形貌Fig.15 Local surface topography of workpiece between prior process and after process

利用该加工实验平台进行初步的加工工艺试验。采用100 mm×10 mm×5 mm的长方体试件，形成3 mm厚的流层。材料为45#钢，试验前将试件表面研磨加工至均匀粗糙度Ra=0.8 μm。240#金刚砂颗粒度为50 μm，抛光液的配置比例为:2.5 kg金刚砂磨料+5升46号液压油，试验过程中由搅拌棒全程搅拌，保证接近于悬浮液，磨料和液体混合良好。试件经加工后表面相貌发生变化，加工前后工件局部表面形貌如图15所示，加工前工件表面有划痕和凹坑，加工后划痕基本消失，文理趋于紊乱，凹坑深度变浅或消失，试件表面趋于光亮，说明表面形貌得到改善。

8 结论

采用VOF多相流模型和RNGk-ε湍流模型，通过对结构化流道的结构进行合理的网格划分与特殊边界条件设置对结构化流道内部的软性磨粒流流动进行了数值模拟，揭示结构化表面近壁区软性磨粒流的压力场及速度场的分布规律，并预测其软性磨粒流的材料去除特性。

(1)不同的软性磨粒流入口位置对工件加工会产生影响。磨粒流靠近壁面时，压力场、速度场，材料去除率的值都在变小，因为越靠近壁面，磨粒流所受到的阻碍就越大，能量减少就越快。

(2)结构化流道中软性磨粒流的压力场、速度场和磨粒流的材料去除率随着加工区域位置的不同而不同，并呈现沿着轴向位置逐渐减弱。

(3)加工区域的入口段压力、速度值存在突变，为此在实际加工中引入了引流模块。结合流场数值计算结果和实验研究结果，证实了通过引入引流模块能提高和改善工件表面的加工质量，数值模拟为深入研究软性磨粒流的基本规律提供一种理论工具。

［1］ Shiou F J，Ciou H S.Ultra-precision surface finish of the hardened stainless mold steel using vibration-assisted ball polishing process［J］.International Journal of Machine Tools and Manufacture，2008，48(7-8):721-732.

［2］Gianpaolo S，Roberto M，Gianmaria C.A surface roughness predictive model in deterministic polishing of ground glass moulds［J］.International Journal of Machine Tools and Manufacture，2009，49(1):1-7.

［3］Brinksmeier E.Polishing of structured molds［J］.CIRP Annals-Manufacturing Technology，2004，53(1):247-250.

［4］ Brinksmeier E.Finishing of structured surfaces by abrasive polishing［J］.Precision Engineering，2006，30(3):325-336.

［5］Ji S M，Xiao F Q，Tan D P.A new ultraprecision machining method with softness abrasive flow based on discrete phase model［J］.Advanced Materials Research，2010，97-101:3055-3059.

［6］武利生，李元宗.磨料流加工研究进展［J］.金刚石与磨料磨具工程，2005，145(1):69-74.

［7］Jain V K，Adsul S G.Experimental investigations into abrasive flow machining(AFM)［J］.International Journal of Machine Tools＆ Manufacture.2000，40(7):1003-1021.

［8］计时鸣，唐 波，谭大鹏，等.结构化表面软性磨粒流精密光整加工方法及其软性磨粒流动力学数值分析［J］.机械工程学报，2010，46(15):178-184.

［9］巴 鹏，邹长星，陈卫丹.截止阀启闭时流动特征的动态数值模拟［J］.振动与冲击，2010，29(10):157-161.

［10］ Victor Y，Steven A O.Renormalization group analysis of turbulence:I. basic theory［J］. Journal of Scientific Computing，1986，1(1):3-51.

［11］ Ferzieger J L，Peric M.Computational methods for fluid dynamics［M］.Heidelberg:Springer-Verlag，1996.

［12］ Gatzen H H，Wu K H，Cvetkovic S.Modeling CMP investigation of the mechanical removal mechanism［C］.Proc.ASPE 20th Ann.Meet.Norfolk，Virginia，USA，2005:500-503.