大型数控车床进给伺服系统建模与分析

刘丽兰，刘宏昭，吴子英，王建平

(西安理工大学 机械与精密仪器工程学院，西安 710048)

进给伺服系统作为数控机床的核心组成部分，是一种精密的位置跟踪与定位系统，其运动精度和定位精度直接关系到机床的加工精度和表面质量。然而，由于相对移动部件间存在着摩擦，特别是在低速进给情况下，非线性摩擦的静、动摩擦力存在差值及Stribeck效应，使机床进给系统的动态及静态性能受到很大影响，这主要表现为低速时出现爬行现象，稳态时有较大的静差或出现极限环振荡等［1］。这些行为破坏了进给运动的准确性和连续性，极大地影响了工件表面的加工精度。

对机床进给伺服系统准确地建模与分析是设计高性能机床、预测其行为的重要前提。许多学者在该方面做了大量的研究工作［2-4］。本文针对某大型数控车床在低速进给时存在的爬行现象，对其建立合理的考虑摩擦和刚度影响的数学模型，通过数值仿真分析低速进给下导致系统爬行的原因，并进行现场实验予以验证，从而为提出消减爬行的合理措施提供理论与实验依据。

1 横向进给伺服系统描述

图1 伺服进给系统机械结构示意图Fig.1 Mechanical schematic of the feed servo system

某型号数控车床为两轴联动，其横向进给伺服系统结构简图如图1所示。采用伺服电机经二级齿轮减速箱驱动滚珠丝杠旋转，丝杠通过螺母副实现工作台的直线运动。工作台处采用贴塑导轨，运行过程中为滑动摩擦。齿轮减速箱总传动比为6，采用双片斜齿轮增加垫片的方法消除间隙。滚珠丝杠导程16 mm，直径80 mm，总长1.773 m，采用两端止推的支撑方式。交流伺服电机为西门子系列电机，调速范围0～1 500 r/min。系统采用全闭环控制，包括电流环、速度环和位置环三环控制，各控制环采用不同算法时其运动精度与定位精度会有差别。

2 横向进给伺服系统建模

2.1 数学模型

为研究进给系统的输出特性，需建立正确的数学模型。对于图1所示的数控机床进给伺服系统，由于其主要运动形式为转动和移动，因此将转动部件轴Ⅰ、轴Ⅱ、和轴Ⅲ向电机轴等效，建立该系统的简化力学模型如图2所示。等效后系统具有电机的转动和工作台的移动两个自由度。该力学模型既涵盖了各个传动环节的运动特性又简单便于分析。

图2 简化力学模型Fig.2 Mechanical model of the feed system

下面根据图2的力学模型建立其数学模型。

首先，交流伺服电机在负载作用下进行旋转运动，建立系统转动方程为:

式中:Jm为等效转动惯量;θm为电机输入转角;Cm为等效粘性阻尼系数;TL为电机负载转矩;kt为电机转角常数;i为电机输入电流。等效转动惯量与等效粘性阻尼系数可由下式计算:

式中:J1为轴Ⅰ的转动惯量;J2为轴Ⅱ的转动惯量;J3为轴Ⅲ的转动惯量;C1为轴Ⅰ的粘性阻尼系数;C2为轴Ⅱ的粘性阻尼系数;C3为轴Ⅲ的粘性阻尼系数;i1为齿轮1和齿轮2的传动比;i2为齿轮3和齿轮4的传动比。

电机轴与丝杠之间由于扭转变形产生的角度偏差为:

式中，θs为丝杠转角。

电机负载转矩为:

式中，Kθ为等效扭转刚度，由下式计算。

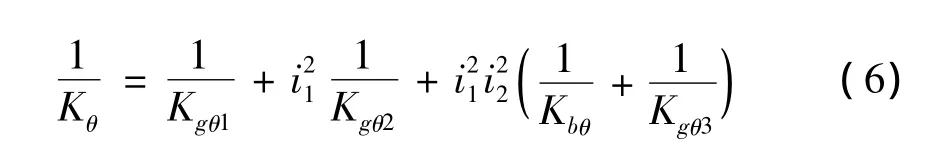
式中:Kgθ1为轴Ⅰ的扭转刚度;Kgθ2为轴Ⅱ的扭转刚度;Kgθ3为轴Ⅲ的扭转刚度;Kbθ为丝杠轴的扭转刚度，计算式为:

式中:a为载荷作用点距离丝杠左端支撑的长度。

如图3所示，由于工作台在运行过程中，a是变化的，所以，丝杠轴的扭转刚度会随着工作台的位置变化而变化。同时，电机负载转矩TL用以驱动工作台轴向运动，有:

图3 工作台进给位置示意图Fig.3 Position of the worktable

式中:Fd为工作台直线运动驱动力;r为转动与移动之间的转换比;l为丝杠的导程;η为传递效率，取η=1。

在电机转矩的驱动下，丝杠的转动转化为螺母(工作台)的轴向移动，但由于轴向弹性变形二者存在位移差，因此工作台的驱动力Fd为:

式中:xs为丝杠转化的轴向位移，xs=rθs;xt为工作台的位移;K1为工作台的等效轴向刚度。K1由下式计算:

式中:Kb为滚珠丝杠的轴向刚度;Kn为螺母组件刚度;Kz为螺母支架和轴承支架轴向刚度;2Kc为一对支撑轴承的轴向刚度。

滚珠丝杠轴向刚度计算式为:

式中:A为丝杠轴截面面积;E为杨氏模量;L为丝杠轴支撑间的跨距。

由式(11)可见，当a变化时，丝杠轴的轴向刚度也随之变化，且当a=L/2时Kb最小。

该进给伺服系统的综合等效传动刚度Ke可由等效扭转刚度Kθ和等效轴向刚度Kl获得:

滚珠丝杠的旋转运动通过螺母转换为工作台的直线移动，建立工作台的运动方程为:

式中:Mt为工作台质量;Ct为工作台阻尼系数;Ff为摩擦力。

结合系统控制形式，可建立系统电流方程为:

式中:L为电动机电感;R为电动机电阻;kpp为位置环增益;kv为速度指令调整增益;kvp为速度环增益;kip为电流环增益;kemf为反电动势;xr为系统输入目标位置;e为位移误差，e(t)=xr(t)-xt(t)。

由以上建模可以看出，一旦系统结构形式和控制参数确定以后，摩擦力是影响工作台输出的关键因素。此外，由于工作台在运行过程中与丝杠的相对位置发生变化导致丝杠的轴向刚度和扭转刚度变化，从而引起综合传动刚度变化，也会影响到工作台的输出运动。因此考虑摩擦对工作台输出影响的同时，分析传动刚度对工作台输出的贡献也很重要。

2.2 摩擦模型

摩擦非线性将对进给系统工作台的运动产生重要影响。由于工作台质量较大，且其与导轨间存在滑动摩擦，受摩擦力作用较其他部位更加明显，因此本文主要考虑工作台与导轨间滑动摩擦。

LuGre模型描述了诸多摩擦现象，包括库仑摩擦、粘性摩擦、预滑动、可变静摩擦力、Stribeck摩擦和摩擦滞后等，较其它模型更能全面体现真实摩擦现象，是目前应用最为广泛的一种动态摩擦模型。此处采用LuGre 摩擦模型［5］。

LuGre模型中摩擦力由鬃毛的变形产生，描述为:

式中:σ0为鬃毛刚度;σ1为微观阻尼系数;σ2为粘性摩擦系数;z为鬃毛平均变形，其变形量z表示为:

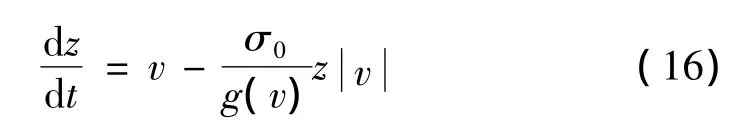
其中，函数g(v)描述了 Stribeck效应［6］:

式中:v为相对运动速度;vs为Stribeck速度;fc为库仑摩擦力;fs为最大静摩擦力。

3 数值仿真

由于获取实际进给系统所有物理参数的难度很大，因此基于已建立的系统数学模型，采用数值仿真方法就摩擦和刚度对工作台输出的影响进行定性地分析。采用Simulink软件建立含摩擦的两自由度系统的闭环控制框图如图4所示，仿真数据如表1所列。

图4 进给系统控制框图Fig.4 Control schematic of the feed servo system

表1 仿真数据Tab.1 Simulation data

3.1 静动摩擦力差值与爬行

静动摩擦力存在差异是非线性摩擦的一个重要特点，它会对系统的动态性能产生很大影响。而静动摩擦力差值的大小是衡量这种影响程度的关键因素。令静动摩擦力的比值为:

为了分析静动摩擦力差值与工作台爬行运动的关系，表2给出了在fc=15 N及Ke=0.2 N/μm的条件下，h从1.2变化到1.8时系统开始发生爬行运动的临界爬行速度。根据表2绘出的变化趋势曲线见图5。

表2 静动摩擦力比值与临界爬行速度的对应数值Tab.2 Values of the ratios of the static to kinematic friction and critical stick－slip velocity

由图5看出，传动刚度恒定时，静动摩擦力比值的变化对系统动力学行为产生的影响较大。随着h的增加，即静动摩擦力差异的加大，工作台的临界爬行速度也随之增加，尤其在h=1.3时较h=1.2时临界爬行速度增加的幅度较大。这种变化导致工作台在低进给速度下更容易发生爬行运动，从而使工作台进给速度的下限范围受到了限制。因此，减小静动摩擦力的差距是减小系统爬行行为的一项重要措施。

图5 静动摩擦力比值与临界爬行速度关系曲线Fig.13 Relation curve of the ratio of the static to kinematic friction versus critical stick-slip velocity

3.2 传动刚度与爬行

为了进一步分析刚度与工作台临界爬行速度之间的关系，通过反复多次仿真，表3给出了在fc=15 N、h=1.6及综合等效传动刚度Ke从 0.4 N/μm 变化到1.6 N/μm的情况下，进给伺服系统发生临界爬行时的速度数值。

表3 综合等效传动刚度与临界爬行速度对应数值Tab.3 Values of the equivalent stiffness and critical stick slip velocity

图6 综合等效传动刚度与临界爬行速度的关系曲线Fig.6 Relation curve of equivalent stiffness versus critical stick-slip velocity

根据表3，图6绘出了综合等效传动刚度与工作台临界爬行速度关系曲线。从图中看出，在静动摩擦力差值不变的情况下，随着刚度的增加工作台发生爬行的临界速度逐渐降低，但其减小的幅度逐渐变小。说明在受摩擦非线性影响的进给系统中，传动刚度的变化也会影响工作台的输出。适当地增加综合等效传动刚度，主要是丝杠的刚度，可使进给系统在较低的进给速度下避免爬行。这对于高精度、低进给要求的机床加工非常有利。

4 实验

为了验证对该类型机床进给系统的建模与数值分析得到的定性结果的正确性，现以某大型数控车床横向进给系统为实验对象，测量工作台在较低进给速度下的临界爬行速度，分析刚度变化与临界爬行速度之间的关系。

4.1 测试方法

数控机床进给系统及测试装置如图7所示。实验中主要使用英国Renishaw XL激光干涉仪进行动态测量。测试过程中机床主轴停止转动，横向进给系统空载运行。

(1)工作台行程为1 000 mm，测试共取8个位置作为测点，如图8所示。

(2)在每个测点处编制机床控制程序使工作台沿着轴线匀速运动。首先从较高进给速度开始运行，运行时间为10.2 s，采用Renishaw XL激光干涉仪测量工作台的动态响应。观察工作台有无爬行行为，若无爬行发生，重新设定进给速度驱动工作台运动，进给速度以0.1 mm/min的步长递减，直至发现工作台出现爬行现象。记录测点位置及临界爬行速度数据。

图9 第1测点响应信号Fig.9 Responses of the test point 1

通过反复测量得到了各个测点处工作台发生临界爬行运动时的位移和速度响应信号，其中第1测点的位移和速度响应信号如图9(a)、(b)所示。

4.2 测试结果

表4给出了在各个测点处工作台的临界爬行速度。根据厂家提供的该型数控机床进给伺服系统的相关数据，由式(12)可以计算出工作台位于8个测点处时进给系统的综合等效传动刚度Ke列于表4中。并且，为了更直观地表达各个量之间的关系，图10绘出了临界爬行速度、综合等效传动刚度与工作台位置之间的关系曲线。

表4 测量与计算数据汇总Tab.4 Measured and computed data

图10 临界爬行速度、综合等效传动刚度与工作台进给位置的关系Fig.10 Relationship of critical stik-slip velocity，equivalent stiffness and the position of the worktable

从图10中的“—*—”曲线可以看出，低速进给下，在8个测点处工作台发生爬行的临界进给速度是不同的，越接近丝杠中点位置临界爬行速度越大(第3测点稍有差异)。原因由于工作台在运行中处于丝杠的不同位置，每一测点的传动刚度不同，如图10中的“—o—”曲线，综合等效传动刚度由丝杠两端向丝杠中间位置逐渐减小。8个测点处的摩擦条件和控制参数一致，因此可以判断是综合等效传动刚度的变化导致了工作台临界爬行速度的变化，且有综合等效传动刚度降低，临界爬行速度增大的趋势。实验结果与第3.2节的数值仿真分析结果一致，从而验证了本文对数控机床进给伺服系统的理论建模与分析是合理适用的。

实验结果可为该类型的数控机床避免低速进给下工作台发生爬行的现象提供一种解决方案，即在经济性和结构方面允许的前提下尽可能地提高滚珠丝杠的刚度。

5 结论

针对某型号数控车床的进给伺服系统在低速进给下出现爬行的问题，对其建立了完善的数学模型。模型中充分考虑了非线性摩擦和传动刚度的影响。通过数值仿真，着重分析了静动摩擦力比值和综合等效传动刚度对进给工作台输出运动的影响规律。仿真结果表明，静动摩擦力差异是导致爬行现象的重要原因，差值越大越容易引起爬行运动。而传动刚度变化则会改变产生爬行的条件，刚度越大，发生爬行所需的静动摩擦力差值就越大。在静动摩擦力差异不变的情况下，刚度增加系统临界爬行速度随之降低，有利于系统稳定。现场实验与数值仿真的结果趋势基本一致，表明本文的理论建模与分析是合理、有效的。

［1］ Armstrong-Helouvry B，Dupont P，Canudas de Wit C.A survey of models，analysis tools and compensation methods for the control of machines with friction［J］.Automatica，1994，30(7):1083-1138.

［2］梅雪松，陶 涛，堤正臣，等.高速、高精度数控伺服工作台摩擦误差的研究［J］.机械工程学报，2001，37(6):76-81.

［3］ Sato R，Tsutsumi M.Mathematical model of feed systems consisting of AC servo motor and linear ball guide［J］.Journal of the Japan Society for Precision Engineering，2005，71(5):633-638.

［4］Kripa K V，Samir A N.The dynamics of lead-screw drives:low-order modeling and experiments［J］.Transactions of ASME JournalofDynamicSystems， Measurement， and control，2004，126(2):388-395.

［5］Canudas D Wit C，Olsson H，Lischinsky P.A new model for control of systems with friction［J］.IEEE Transactions on Automatic Control，1995，40(3):419-425.

［6］ Bliman P A，Sorine M.Friction modeling by hysteresis operators.Application to Dahl，Sticktion，and Stribeck effects［C］//In Proc. Conf. Modelsofhysteresis， Trento，Italy，1991.