一种基于本征波匹配的EMD边界处理方法

钟佑明，赵 强，周建庭

（1.重庆交通大学 信息科学与工程学院，重庆 400074；2.重庆交通大学 土木工程学院，重庆 400074）

希尔伯特－黄变换（Hilbert－Huang Transform，简称HHT）是上世纪末由Huang等人［1－2］为更精准地分析非线性非平稳信号而提出的一种信号分析方法。这一方法已被许多学者应用于各种工程和生活领域，取得了较为理想的效果。HHT包含若干关键技术，EMD（Empirical Mode Decomposition，即经验模态分解）边界处理就是其中之一。目前已经有不少EMD边界处理的方法，如特征波法［1］、波形匹配预测法［3－4］、神经网络分析方法［5］、镜像闭合延拓法［6］、多项式拟合法［7］、包络极值延拓法［8］、相似极值延拓法等［9］，虽然这些方法都有一定效果，但同时又有明显的理论缺陷，如特征波法、镜像闭合延拓法、包络极值延拓法等都仅利用了与边界相邻的少数一些内部波来预测信号边界的包络或均值，使得它们的应用效果不太理想。本文第一作者在文献［10］中曾提出了一种改进的波形匹配预测法——本征波匹配预测法。但由于当时对该方法的有效性还有些怀疑，尤其是还不知道如何合理构造仿真信号来验证该方法，因此文献［10］只是提出了初步算法而没有进行深入的算例验证。本文最终弥补了这一重要不足，使文献［10］的研究得到较大程度地深化和完善。

1 EMD及其边界处理问题

EMD的主要内容是通过筛选将信号分解为有限个固有模态函数（IMF）和趋势项之和，其中IMF被认为是构成非线性非平稳信号的基本信号，它具有唯一的瞬时频率，而趋势项反映信号变化的趋势［1］。所谓IMF，是指满足如下两个条件的信号：

① 信号中，零点数与极点数相等或至多相差1；

② 信号上任意一点，由局部极大值点确定的包络线和由局部极小值点确定的包络线的均值都为零。

EMD的过程简介如下：对于给定的实信号s（t），例如图1（a）所示信号，首先确定出其上的所有极大值点和极小值点，然后将所有极大值点和所有极小值点分别用一条光滑曲线（如三次样条曲线）联接起来，使两条曲线间包含所有的原信号，如图1（b）虚线所示。将这两条曲线分别作为s（t）的上、下包络线，计算出它们的平均值曲线m1（t），如图1（b）点划线所示。用s（t）减去m1（t）得到：

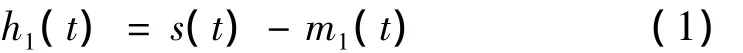
h1（t）的波形如图1（c）所示。以上过程称为“筛选”。理想情况下，所筛选出的h1（t）应该是一个IMF，因为h1（t）的构造过程就是使它满足IMF的条件。但实际上往往还需对h1（t）按以上方法进行多次筛选［1］，直到其满足某个终止准则（如SD＜0.2［1］），就认为成为了一个IMF，记为c1（t），如图1（d）所示。将s（t）减去已经筛选出的IMFc1（t）后再用同样的方法可以依次筛选出s（t）中的其余IMF及趋势项。最终s（t）可以表示为：

图1 EMD过程示意图Fig.1 The illustration of EM

从以上介绍可以看出，EMD是利用极值点拟合信号包络线或均值曲线对信号进行分解的。实际中获得的信号往往是被截断后的信号，这类信号内部的极值点总是能获得，但边界外的极值点或边界包络与均值只有经过预测才能得出，这就是HHT中的EMD边界处理问题，它是HHT的一个重要问题［1］。如引言所述，目前已经有若干EMD边界处理方法，但这些方法还有待改善。笔者通过分析认为，在已有的EMD边界处理方法中波形匹配预测法是一种相对更实用的方法，因为它利用与边界波最相匹配的内部波来预测信号的边界均值，与许多实际信号具有波形重复性的规律相一致。但目前的波形匹配预测法是采用边界复合波与内部复合波的匹配性来预测边界均值的，使其不适用于有调幅或叠加波的复合信号［10］。

2 基于本征波匹配的EMD边界处理方法

针对波形匹配预测法的不足，本文第一作者在文献［10］中曾提出了一种改进的波形匹配预测法——本征波匹配预测法。它是基于对IMF本身结构的深入认识和所建立的本征波概念而提出的。

一个IMFc（t）可以看成是由cosφ（t）经包络线a（t）调制而成的，如图2（a）、图 2（b）所示，cosφ（t）中包含了c（t）的全部频率信息，因此称之为本征信号［10］。而cosφ（t）中的频率往往是时变的，不同时刻可以有不同的频率，每处的频率有一个对应尺度的子波，如图2（a）中所示的从一个极大值点到下一个相邻的极大值点形成的信号段ABC（后面本文理论的应用例子表明，对这种“子波”无需清晰定义，只需大致定义即可），且同一cosφ（t）中不同时刻的子波可以相互叠加。因此可以认为本征信号cosφ（t）又是由一些不同尺度的子波叠加构成，这些子波在文献［10］中称为本征波。这样，在HHT中任何一个信号f（t）都可以看成是由一些本征波相互叠加形成本征信号，本征信号经过调幅后形成IMF，如图2（b）所示，IMF再相互叠加就形成复合信号f（t），而本征波在复合信号中必有一个一一对应的复合波，如图2（c）所示A″B″C″。

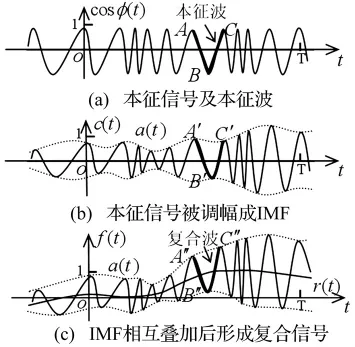
图2 HHT中的复合信号形成过程Fig.2 The forming process of composite signal in HHT

下面以起始点的EMD边界处理为例对本征波匹配预测法的算法作一介绍。

设信号起始点及连续相邻的两个极值点分别为s（0）、e（t1）、e（t2），则这三点构成一个边界复合波s（0）e（t1）e（t2），其隐含一个边界本征波，让s（0）e（t1）·e（t2）在极值点序列中以步长2逐渐向右移动，所移之处都有一个由顶点e（ti－1），e（ti），e（ti+1）构成的内部复合波e（ti－1）e（ti）e（ti+1）［隐含一个内部本征波］与之对应，如图3（a）所示。本征波匹配预测法就是为了寻找一个其本征波与边界波的本征波匹配误差最小的内部波来预测边界均值。为此，首先将波形s（0）e（t1）e（t2）减去直线y（t）=e（t1）（相当于去掉叠加波），再除以e（t1）－e（t2）（相当于消除调幅波），最终得波形s0e1e2，它可以被认为就是波形s（0）e（t1）e（t2）所隐含的近似边界本征波，如图3（b）所示；同理，将波形e（ti－1）e（ti）e（ti+1）减去直线y（t）=e（ti）并除以e（ti）－e（ti+1）得波形e（ti－1）e（ti）e（ti+1）所隐含的近似内部本征波ei－1eiei+1。这样边界波s（0）e（t1）e（t2）与内部波e（ti－1）e（ti）e（ti+1）之间的匹配误差就可以采用如下本征波匹配误差估计公式计算：

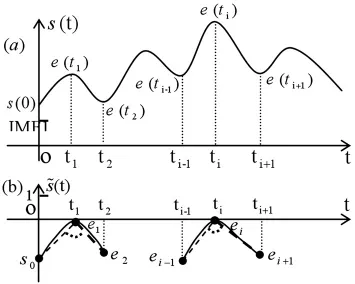
图3 本征波匹配预测法示意图Fig.3 The illustration of character wave matching prediction

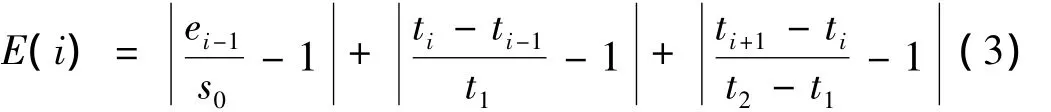
当计算完所有误差E（i）后，确定出最小误差E（k），此处的内部波即被认为与起始边界波最匹配，因此可以利用此内部波的均值预测起始点处的均值，预测公式如下：

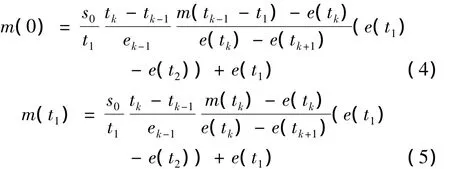
这里不仅给出了估计起始点处均值的公式，还给出了估计第一个极值点对应均值的公式，以提高边界均值曲线拟合的稳定。用同样的方法可以估计出信号右端点处的均值。

根据以上介绍可以看出，本征波匹配预测法是利用信号边界波和内部波之间的本征波匹配性来预测信号边界处的包络值和均值，既继承了波形匹配预测法的优点，同时又克服了波形匹配预测法在计算匹配误差时忽略了信号调制与叠加对波形匹配误差的影响问题，使得本征波匹配预测法的适用范围得以大幅扩大。

3 本征波匹配预测法的算例验证

为了验证本征波匹配预测法的可行性和进步性，这里分别用本征波匹配预测法和两种具有代表性的EMD边界处理方法——包络极值延拓法与波形匹配法对图4（a）、图5（a）所示的两个含调幅与叠加波的仿真信号和图6（a）所示的一实测空调振动信号进行EMD，所得结果依次如图4（b）、图4（c）、图4（d）、图5（b）、图5（c）、图5（d）和图6（b）、图6（c）、图 6（d）所示，其中筛选终止准则为SD＜0.2。由图4（d）可以看出，以本征波匹配预测法进行EMD边界处理时，所得趋势项与原始信号的总体趋势非常一致，且所得IMF1，IMF2的左右两边界波形也比较合理，而由图4（b）、图4（c）可以看出，以包络极值延拓法或波形匹配法进行EMD边界处理时，所得IMF与趋势项在右端均容易出现明显变异。观察图5也可以得到同样的结论。再观察图6可以看出，以包络极值延拓法进行EMD边界处理时，所得IMF2的左端、趋势项的左右端均出现了明显变异；以波形匹配法进行EMD边界处理时所得IMF2左端也变异明显，虽然所得趋势项的左右端变异不明显，但同用本征波匹配预测法所得图6（d）所示的趋势项相比，仍不如后者更接近肉眼所观察到的原信号两端的变化趋势。另外与图6（b）、图6（c）相比，图6（d）中IMF2的左端变异也有明显改善。因此，无论对于仿真信号还是实测信号，用本征波匹配预测法进行EMD边界处理均能取得比其他EMD边界处理方法更满意的效果。

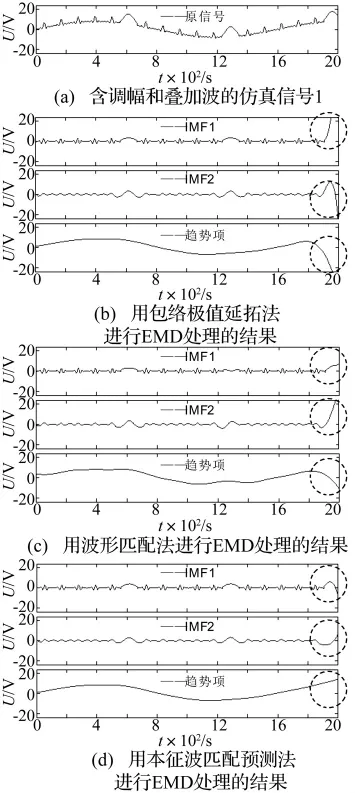
图4 三种EMD边界处理方法在对一仿真信号进行EMD时的结果比较Fig.4 The EMD result comparison of three sorts of EMD end process methods to a simulated signal

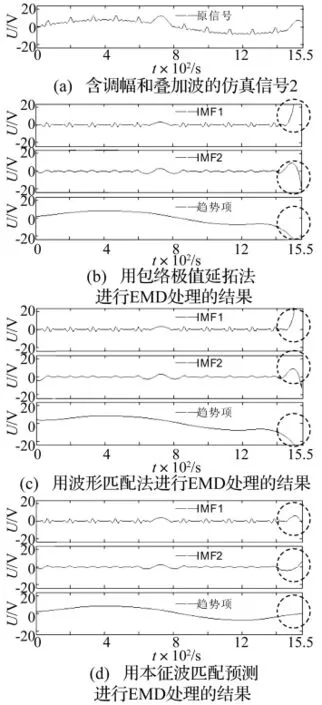
图5 三种EMD边界处理方法在对另一仿真信号进行EMD时的结果比较Fig.5 The EMD result comparison of three sorts of EMD end process methods to another simulated signal

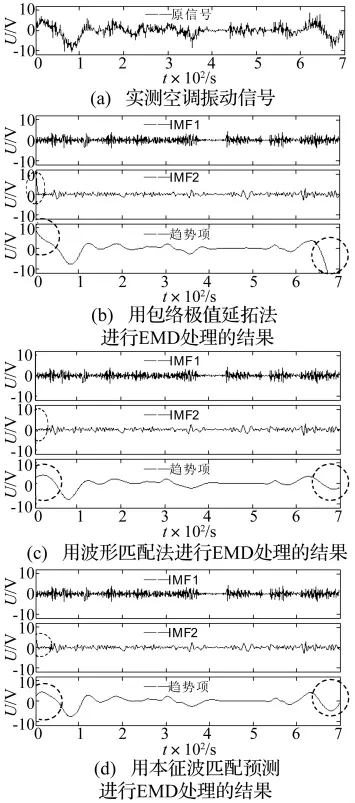
图6 三种EMD边界处理方法在对实测信号进行EMD时的结果比较Fig.6 The EMD result Comparison of three sorts of EMD end process methods to a test signal

4 结论

本文着重对文献［10］中提出的一种基于本征波匹配的EMD边界处理方法——本证波匹配预测法进行了介绍，特别是介绍了将该方法和其他两种有代表性的EMD边界处理方法——包络延拓法和波形匹配预测法应用于仿真信号和和实测信号的算例对比，从而验证了本证波匹配预测法的先进性。本文工作使文献［10］中的相关研究得到较大程度地深化和完善。

［1］Huang N E，Zheng S，Long S R，et al.The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis［J］.P roc.R.Soc.Lond.A ，1998，454：903－995.

［2］Pen Z K，Tse P W，Chu F L.An improved Hilbert Huang transform and its application in vibration signal analysis［J］.Journal ofSoundandVibration， 2005， 286 （122）：187－205.

［3］盖 强，马孝江，张海勇，等.一种消除局域波法边界效应的新方法［J］.大连理工大学学报，2002，42（1）：115－117.

［4］王 婷，杨莘元，李冰冰.一种改善EMD端点效应的新方法［J］.哈尔滨理工大学学报，2009，14（5）：23－26.

［5］邓拥军，王 伟，钱成春，等.EMD方法及Hilbert变换中边界问题的处理［J］.科学通报，2001，46（3）：257－263.

［6］黄大吉，赵进平，苏纪兰.希尔伯特－黄变换的端点延拓［J］.海洋学报，2003，25（1）：1－11.

［7］刘慧婷，张 旻，程家兴.基于多项式拟合算法的EMD端点问题的处理［J］.计算机工程与应用，2004，40（16）：84－86.

［8］徐世艳.基于延拓技术的经验模态分解改进算法［J］.吉林大学学报，2009，27（4）：359 －365.

［9］沈 路，周晓军，张志刚，等.Hilbert-Huang变换中的一种端点延拓方法［J］.振动与冲击，2009，28（8）：168－175.

［10］钟佑明.希尔伯特－黄变换局瞬信号分析理论的研究［D］.重庆：重庆大学，2002.