SGWT在爆破振动信号信噪分离中的应用研究

2012-02-12谢全民钟明寿陆凡东毛益明

振动与冲击 2012年1期

谢全民，龙源，钟明寿，陆凡东，毛益明

（1.解放军理工大学工程兵工程学院，南京 210007；2.中国人民解放军63988部队，山西晋城 048000）

工程爆破中，减小和控制爆破振动对工程安全和保护环境具有重要意义。爆破振动信号分析既是研究爆破振动危害控制的基础，也是控制爆破振动危害的前提［1-3］。由于爆破振动效应状态监测过程中易受外部环境和测试系统的影响，测试信号中不可避免地含有噪声。因此，滤除爆破振动信号中噪声的影响，提高爆破振动数据的可靠性和准确性，是爆破振动效应分析研究的基础［4］。爆破振动信号是一种短时非平稳信号，有效信号和噪声经过小波变换各自系数将呈现不同的传播特性，据此使用小波阈值去噪具有良好的效果［5-6］。工程爆破中为建立爆破振动预报与控制平台，要求在传统小波去噪算法的基础上提高信号分析处理的效率和质量，实现在线处理对实时性、准确性的要求。

Sweldens于1996年提出的小波提升或者提升算法Lifting Scheme，被称作二代小波变换（Second Generation Wavelet Transform，SGWT），继承了经典小波多分辨率特性，可以实现原地运算，占用空间小，变换速度快［7-8］。与一代小波构造方法的主要区别在于它不依赖于傅氏变换，小波基函数不再由某一个函数的平移和伸缩而产生。提升小波算法可以通过设计不同的预测算子和更新算子得到具有某些特殊功能的小波函数［9-10］，更好地解决实际问题。

Daubechies和Sweldens证明了任何离散小波都可以用提升方案来实现，增强了二代小波的适用性。目前提升算法主要应用在机械振动信号分析，故障诊断等方面［11-14］，SGWT在爆破振动信号分析方面的应用还没有相关报道。

本文构造了基于插值细分法的提升小波，同提升db小波一起用于实测爆破振动信号的分解-阈值去噪-重构，对SGWT在爆破振动信号分析预处理中的应用进行了尝试，取得了满意效果。

1 爆破振动信号的提升小波变换

设爆破振动信号采样序列{s（k），k∈Z}，基于提升算法的小波分解由三步组成：

（1）剖分（split）：将采样序列{s（k），k∈Z}剖分为奇样本序列S0={s0（k），k∈Z}和偶样本序列Se={se（k），k∈Z}，其中：

（2）预测（predict）：也称作对偶提升，设P（·）为预测器，用se（k）预测s0（k），定义预测偏差为细节信号d（k）：

（3）更新（update）：也称作提升，设U（·）为更新器，在细节信号序列D={d（k），k∈Z）的基础上更新se（k），其结果定义为逼近信号c（k）：

小波变换的重构过程由恢复更新、恢复预测、奇偶采样序列合并三步构成，重构公式可由分解式（1）～式（4）变换得到。

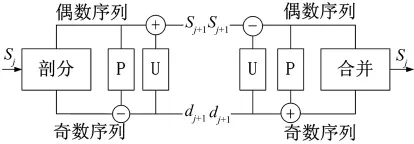
图1 提升小波分解重构示意图Fig.1 Lifting wavelet decomposition and reconstruction

2 广义小波与提升小波构造

Sweldens指出在等间隔采样和无加权函数的情况下，任何一种提升格式都对应着一个广义小波［15］，研究者可以根据需要，构造新的小波。SGWT的关键在于确定预测系数和更新系数，插值细分法是提升模式构造广义小波的常用方法，由它构造的尺度函数和小波函数具有良好的紧支撑性，小波变换具有线性相位，可以有效避免变换过程中的相位失真［16］。

2.1 基于插值细分小波

已知N+1个点x0，x1，…，xN的函数值为y0，y1，…，yN且yi=f（xi），i=0，…，N，则存在唯一一个次数不大于N的多项式Ln（x），使Ln（xi）=f（xi），那么：

式中：

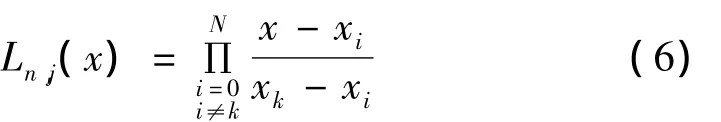
每次插值细分，取N个（N=2D，D∈Z+）等间隔样本yj，k-D+1，…，yj，k，…，yj，k+D，其对应的采样时刻为xk+1，xk+2，…，xk+N，xk为任意的起始时间，通过细分产生新的采样值处于已知样本的中间，插值点为：x=xk+（N+1）/2，则预测系数可由式（7）确定，即：

N=6.8时，根据式（7）求得预测系数如表1所示。

设信号S为一个σ序列，即：

由图1小波重构部分，重构关系简化为：

根据上式对S进行插值细分，即利用k-1，k，k+1，k+2 四点的sj，k值预测sj+1，2k+1，插值边界采用补零的方法进行处理，经过20次迭代后生成尺度函数φ（x）波形见图2、图3。

构造小波函数，需要先设计更新算子U，更新算子的作用是保证小波变换前后信号的低阶消失矩不变。当N=（N为预测器的个数，为更新器的个数）时，可以直接将预测系数除以2作为提升系数［17］。

其中：

式中，U和D分别为更新算子运算系数和细节信号序列。与尺度函数的构造类似，设细节信号为σ序列，近似信号S为零序列，进行一次提升格式反变换，信号的偶序列为：

该序列经过预测算子P（·）进行恢复预测运算，得到信号的奇序列为：

对s0按照式（9）进行插值细分，经过20次迭代可得到相应的小波函数，如图2、图3所示。

图2 SGW（6，6）尺度函数φ（x）与小波函数ψ（x）Fig.2 Scaling function and wavelet function of SGW（6，6）

图3 SGW（8，8）尺度函数φ（x）与小波函数ψ（x）Fig.3 Scaling function and wavelet function of SGW（8，8）

基于提升模式的尺度函数和小波函数是双正交的、对称的、紧支撑的，并且具有冲击形状［9，15］。当N和较小时，尺度函数和小波函数的支撑区间较小；反之，支撑区间较大，具有较好的连续性。一般而言，支撑区间小的小波函数适合于处理非平稳信号，小波系数能够有效地描述信号的瞬态分量，而支撑区间大且连续较好的小波适合于描述稳态信号。爆破振动信号具有典型的短时非平稳特性［18，19］，本文选用 SGW（6，6）和SGW（8，8）进行爆破振动信号分析。

2.2 提升db小波

Daubechies系列小波具有较好的紧支性、光滑性及近似对称性，并已成功应用于包括爆破振动信号在内的非平稳信号问题［6，19-21］。该小波系列按正整数N具有不同的序列（dbN），本研究采用Matlab中提供db小波的提升方案（Daubechies lifting schemes）liftingdb6、liftingdb8，同基于插值细分的二代小波 SGW（6，6）、SGW（8，8）进行爆破振动信号去噪。

基于插值细分的二代小波变换，当（N，）给定后，运算量与log2（N-1）/（Nmax-1）成正比，Mallat小波分解运算量与Nlog2N成正比，在同样数据长度下，提升db小波比传统db小波变换速度提高很多，但和相同支集的插值细分小波相比，运算量较大，运算速度较慢［5，7］。基于插值细分的二代小波变换具有更高的信号处理效率。

表1 预测系数Tab.1 Predict coefficients

3 基于提升算法的爆破振动信号去噪

传统小波去噪中，小波分解是采用信号与小波基进行卷积运算，因此小波分解的结果与所采用小波基的形状密切相关，一旦选用不适当的小波基函数会冲淡振动信号的局部特征信息，造成原始信号的细节信息丢失。为克服上述缺陷，依据基偶空间的相关性［22］，利用上述构造的插值细分小波SGW和提升db小波进行爆破振动信号的二代小波阈值去噪。

图4为典型的爆破振动实测信号，信号采样频率为1 024 Hz，采样时间长度取2 000个采样点，具体的爆破振动信号如图4所示。振动波形中混杂有毛刺及由于测试系统原因而带来的方波干扰信号。图5为采用SGW（6，6）分解三层后绘制的三维时频能量谱，从图中可以看出该信号中含有200 Hz～250 Hz频段内的高频噪声分量。

图4 实测爆破振动含噪信号Fig.4 Measured blasting induced vibration signal

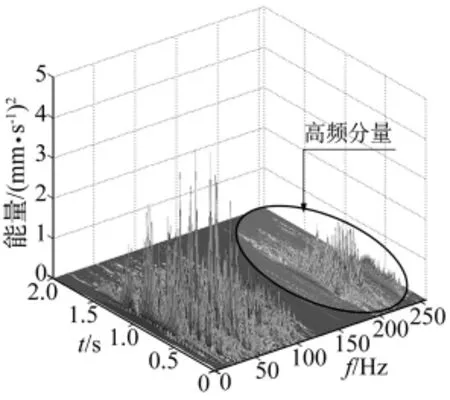
图5 爆破振动含噪信号三维时频谱Fig.5 3D time-frequency spectrum of blasting induced vibration signal

3.1 提升小波降噪算法

对爆破振动信号小波降噪过程如下：

（1）采用提升算法对信号进行多尺度分解；

（2）对分解所得高频细节信号进行阈值处理；

（3）将逼近信号和经阈值处理后的细节信号进行重构得到降噪后的爆破振动信号；

（4）去噪效果分析。

3.2 提升小波变换

采用Matiab编程，根据提升小波变换原理及插值细分小波构造算法，分别使用上述构造的基于插值细分的 SGW（6，6）、SGW（8，8）和提升 db6、db8 小波进行提升小波分解，分解层数为3层，如图6～图9所示。a3为第3层逼近信号，体现爆破振动信号的低频分量，d3～d1为细节信号，体现爆破振动信号的高频分量。

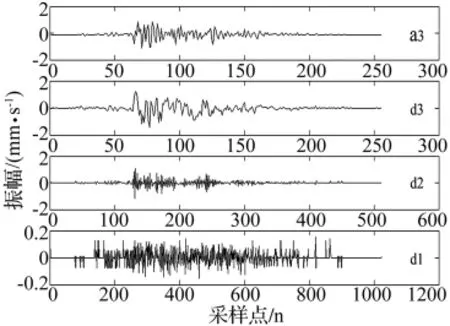
图6 基于SGW（6，6）的爆破振动小波分解Fig.6 Wavelet decomposition of blasting induced vibration based on SGW（6，6）

图7 基于SGW（8，8）的爆破振动小波分解Fig.7 Wavelet decomposition of blasting induced vibration based on SGW（8，8）

图8 基于liftingdb6的爆破振动小波分解Fig.8 Wavelet decomposition of blasting induced vibration based on liftingdb6

3.3 阈值去噪

对含噪信号进行二代小波变换时，噪声也会产生高频系数，故高频细节分量是有用信号和噪声高频系数的叠加，需要选择合适的阈值，使噪声能与有效信号相对应的小波系数合理地区分，实现爆破振动信号的信噪分离。

Donoho和Johnstone提出软阈值处理法［23］：

图9 基于liftingdb8的爆破振动小波分解Fig.9 Wavelet decomposition of blasting induced vibration based on liftingdb8

其中各个尺度的阈值按下式确定：

Tj为各分解尺度对应的阈值，j为分解尺度。

爆破振动信号的噪声方差 σ未知，由式（16）进行估计，median（·）为中值函数。

根据式（14）～式（16），可在提升小波分解的基础上对高频系数实现阈值去噪。

图10表示分别采用基于插值细分的二代小波SGW（6，6）、SGW（8，8）和基于提升变换的 db小波 liftingdb6、liftingdb8经过3层提升小波变换之后，由尺度j=3的逼近信号a3和各个尺度阈值处理后的细节信号3、2、1重构获得去噪处理后的爆破振动波形。由图10中二代小波滤波后的振动波形可以看出，已经基本消除了爆破振动监测信号中由于测试系统和环境噪声带来的干扰。图10中降噪后的波形曲线相对图4中含噪的爆破振动波形曲线更加光滑，峰值上升和衰减等振动特征在去噪后的振动信号中表现得更加清晰，得到的有用信息图10客观反映了实测爆破振动信号的主要成分。

图10 降噪后的爆破振动信号Fig.10 De-noised blasting induced vibration signals

图11为采用SGW（6，6）小波去噪后的三维时频谱，与图5中原爆破振动测试信号的三维时频谱进行比较，可以看出，经过二代小波去噪后200 Hz～250 Hz频段内的高频噪声被基本滤除，爆破振动信号主要能量集中在0 Hz～100 Hz频段内，爆破振动信号能量随时间、频率变化而体现的起伏衰减特征可以明显地得到识别。

图11 降噪后的爆破振动三维时频图Fig.11 3D time-frequency spectrum of de-noised blasting induced vibration signal

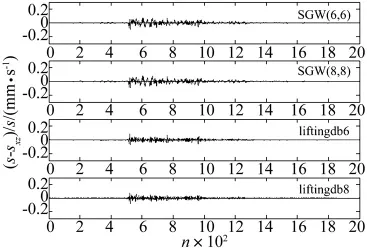
图12 去噪前后相对误差Fig.12 Relative error after and before de-noising

图12为采用上述4个二代小波进行爆破振动信号去噪前后的相对误差分析，可以看出提升db小波相对插值细分小波SGW去噪前后的相对误差较小。为定量研究SGWT在爆破振动信号去噪分析中的应用效果，引入均方根误差（RMSE）、信噪比（SNR）、峰值误差（PE）作为评价标准。

式（17）～式（19）中{si}（i=1，2，…，N）为实测爆破振动信号采样值，{i}（i=1，2，…，N）为经过去噪后的重构信号，N为采样点数。

图13 降噪效果对比Fig.13 Comparison of de-noising effect

分析图10中4个提升小波去噪后的振动信号重构图和图13中降噪效果对比，可以得出：

（1）所采用的基于4个提升小波基的二代小波阈值去噪均能有效滤除爆破振动测试信号中包含的高频噪声。对同一爆破振动信号进行去噪分析，在选定同样阈值条件下，liftingdb6小波可以得到最小的RMSE，最高的SNR和最小的PE，去噪效果较其它提升小波改善明显。对于插值细分小波系列，SGW（6，6）优于SGW（8，8）；对于提升db小波系列，liftingdb6优于liftingdb8。

（2）基于提升算法的db小波相对基于插值细分法构造的SGW在去噪过程中获得相近的RMSE、PE，但提升db相对插值SGW提高了SNR。主要原因在于提升db的小波函数波形［16］比基于插值细分法构造SGW的小波函数波形与爆破振动波形具有更强的相似性。

4 结论

（1）根据二代小波变换（SGWT）原理，通过插值细分法构造的二代小波SGW（6，6）、SGW（8，8）同提升db小波liftingdb6、liftingdb8用于爆破振动信号信噪分离，研究表明，插值细分小波SGW和提升db小波均可有效滤除实测爆破振动信号中包含的噪声，达到了预期的研究目的。

（2）小波基的选择会影响去噪效果，根据爆破振动信号短时非平稳特性的要求，在SGWT阈值去噪过程中，选取提升小波基的支集不宜过长。

（3）提升db小波函数与爆破振动波形具有更强的相似性，在二代小波阈值去噪过程中能提高信噪比。插值细分小波相对提升db小波有更高的信号处理效率，因此在满足信号处理效率和质量要求的范围内，采用SGWT对爆破振动信号进行分析时，应当合理利用二者的优势。

［1］张耀平，曹平，高赛红.爆破振动信号的小波分解及各频段的能量分布特征［J］.金属矿山，2007，377（11）：42-43.

［2］史秀志，薛剑光，陈寿如.爆破振动特征参量的粗糙集模糊神经网络预测［J］.振动与冲击，2009，28（7）：73-76.

［3］晏俊伟，龙源，方向.基于小波变换的爆破振动信号能量分布特征分析［J］.爆炸与冲击，2007，27（5）：405-410.

［4］中国生，徐国元，赵建平.基于小波变换的爆破地震信号阈值去噪的应用研究［J］.岩土工程学报，2005，27（9）：1055-1059.

［5］孔国杰，张培林，曹建军.基于提升小波变换的信号降噪及其工程应用［J］.计算机工程与应用，2008，44（10）：234-237.

［6］谢全民，龙源，钟明寿.基于小波、小波包两种方法的爆破振动信号对比分析［J］.工程爆破，2009，15（1）：5-9.

［7］ Daubechies I，Sweldens W.Factoring wavelet transforms into lifting steps ［J］. Journal of Fourier Analysis and Application，1998，4（3）：247-269.

［8］曹建军，张培林，任国全.提升小波包最优基分解算法及在振动信号降噪中的应用［J］.振动与冲击，2008，27（8）：115-116.

［9］Sweldens W. The lifting scheme：a custom-design construction of biorthogonal wavelets［J］.Applied and Computational Harmonic Analysis，1996，15（3）：186-200.

［10］耿艳峰，冯叔初.小波构造综述［J］.石油大学学报（自然科学版），2004，28（1）：127-131.

［11］粟鸣，郭东敏，权建峰.基于提升小波的改进半软阈值降噪方法［J］.探测与控制学报，2009，31（4）：54-57.

［12］段晨东，何正嘉.基于提升模式的特征小波构造及其应用［J］.振动工程学报，2007，20（1）：85-90.

［13］段晨东，李凌均，何正嘉.第二代小波变换在旋转机械故障诊断中的应用［J］.机械科学与技术，2004，23（2）：224-229.

［14］荆双喜，李胜华，华伟.第二代小波降噪法在故障诊断中的应用［J］.煤矿机电，2007，2：3-5.

［15］ Sweldens W.The lifting scheme：a construction of second generation wavelets［J］.SIMA J Math Anal，1996，29（2）：511-546.

［16］何正嘉.小波有限元理论及其工程应用［M］.北京：科学出版社，2006.

［17］ Sweldens W，Schröder P .Building your own wavelets at home［DB/OL］.http：//cm.bell-labs.com/who/wim/papes.html/athome，1998-01-05.

［18］娄建武，龙源.爆破震动信号的特征提取及识别技术研究［J］.振动与冲击，2003，22（3）：80-82.

［19］龙源，娄建武，徐全军.小波分析在结构物对爆破振动响应的能量分析法中的应用［J］.爆破器材，2001，30（3）：1-5.

［20］何军，于亚伦，梁文基.爆破振动信号的小波分析［J］.岩土工程学报，1998，20（1）：47-50.

［21］黄文华，徐全军.小波变换在判断爆破地震危害中的应用［J］.工程爆破，2001，7（1）：24-27.