新型滚珠式多向动力吸振器的理论研究

张小龙，东亚斌，张晓钟，李雨田

（西安建筑科技大学 机电工程学院，西安 710055）

为了降低机械和结构的振动响应，特别是受到各种条件制约难以回避共振时，现实的方法是安装各种动力吸振器。在主振动系上附加吸振器后，通过适当选择吸振器的动力参数，在主振系共振频率点附近就可以达到减小其强迫振动响应的目的。由于被动式动力吸振器的结构简单，稳定性和可靠性高，不需要外部动力源，能有效地抑制频率变化较小的机械或结构的振动，因此很早就在许多领域获得了应用，同时对各种被动式动力吸振器的研究与开发也一直受到人们的关注［1－2］。

为了达到动力吸振的目的，佐藤久雄等［3］利用两球同向旋转时在接触点处逆向运动产生阻尼力，设计了一种两球转动式吸振器（two-ball rolling type swing damping equipment）。松久寛等［4］开发出了解决索道缆车振动问题的圆弧轨道型吸振器。荒川利治等［5］利用水平半圆弧弹簧和电磁阻尼，开发了一种水平二维免振台，用于抑制因风、地震和地基振动引起的住宅振动。张小龙等［6－7］通过理论分析与数值计算研究了滚珠控制转子不平衡振动的理论与技术。

为了降低吸振器的成本，简化结构，本文设计了一种由简单几何体球面和球体组成的滚动质量型吸振器，称为滚珠式多向动力吸振器，可以用于塔柱类设施的多个方向振动控制，具有一定的通用性。本文在对其进行动力学建模、分析与计算的基础上，运用定点理论优化设计了吸振器参数，还讨论了参数对吸振效果的影响。

1 吸振器及其理论分析

1.1 吸振器

如图1所示，在振动主体（质量为M）的凹球面（半径为R）内有一吸振球（质量为m、半径为r，绕其直径的转动惯量为I），振动主体用刚度为k的弹簧和阻尼系数为c的阻尼器与基础相联（图中阻尼器略）。由于图1中吸振球可沿凹球面向任何方向运动，所以系统在水平面内沿任何方向振动时，吸振球均有吸振作用。

图1 滚珠式多向动力吸振器原理图Fig.1 Mechanism of dynamic multi-direction vibration absorber with a ball

1.2 运动方程式及吸振性能分析

为了简化分析过程，这里只分析系统在一个方向的振动及其吸振作用，模型如图2所示，吸振球在半径为R的圆弧面内运动，系统平衡时，吸振球处于圆弧最底部，弹簧k无伸长，以此位置为坐标原点，建立图示的固定坐标系O-XY，取振动主体的水平位移z及吸振球心绕凹球面中心O'的角位移θ为广义坐标。

图2 系统在单方向的振动模型Fig.2 Mechanical model of the system in one direction

一般情况时，设吸振球中心在坐标系O－XY中的坐标为（x，y），则：

假设吸振球沿圆弧面轨道作无滑动的纯滚动，并设吸振球从圆弧面最底部的平衡位置开始滚动到图2所示位置时滚动角度为φ，如图3示，则有下述关系：

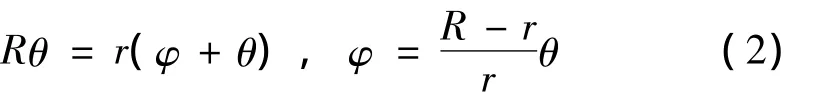
系统的动能T、势能U和耗散函数V分别为：

其中I=2mr2/5，cb为吸振球运动阻尼。根据拉格朗日方程，当振动主体上作用外激励Fcosωt时，系统运动微分方程为：

图3 吸振球的纯滚动Fig.3 The pure rolling of the ball damper

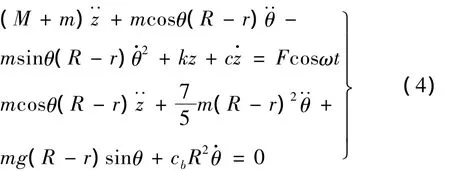
考虑到吸振球在θ=0附近作微小振动，设θ为微小量，即 θ=O（ε），取 sinθ≈θ，cosθ≈1，略去O（ε3）及其以上量级小量，则上式对应的无量纲方程式为：

其中：

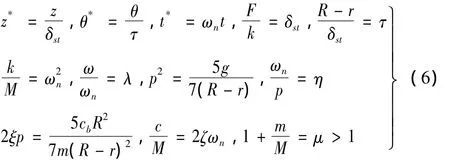
上式中δst为大小是外激励力幅值F的静力作用时主振系弹簧的静变形，ωn是主振系的固有频率，p是吸振球的固有频率，ζ是主体的阻尼比，ξ是吸振球的阻尼比，λ是激励频率ω与主振系的固有频率ωn之比，η是主振系的固有频率与吸振球的固有频率比，μ是吸振球、振动主体质量和（M+m）与主体质量M之比。

设方程（5）的解为：

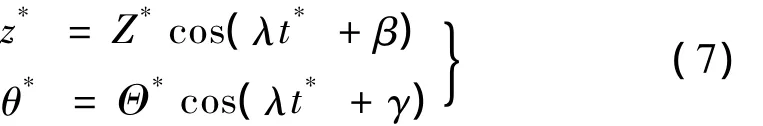
则振动主体和吸振球的振幅为：

式中无量纲参数A，B，C为：

振动主体振幅Z*随参数λ和ξ的变化规律如图4所示。当阻尼比ξ较小时，Z*出现两个峰值，且Z*的峰值随着ξ的增大而减小。若ξ再进一步增大，振动主体M和吸振球m之间的运动相对困难，Z*仅出现一个峰值，且随ξ的增大而增大。所以当ξ无穷大时，M和m之间不出现相对运动，成为质量为（M+m）单自由度系统。图4中出现不随ξ变化的两个定点P和Q。在ζ=0的条件下，分别令式（8）中的ξ=O和ξ→∞的振幅Z*相等，得出求解定点频率比λP和λQ值的方程式为：

将λP、λQ值代入下式，即可得两定点的振幅为：

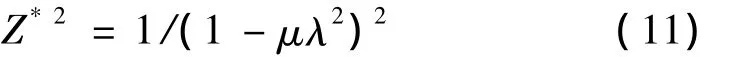
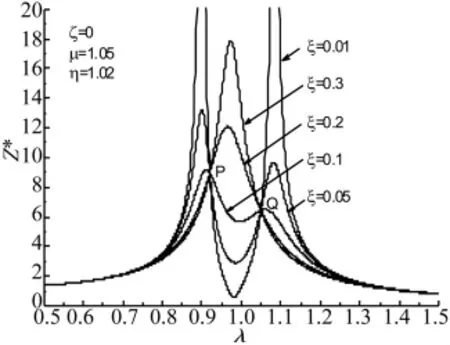
图4 振动主体的振幅变化规律Fig.4 The variation laws of amplitude curve of main vibration system

吸振球的实际振幅Θ（=τΘ*）的变化规律如图5所示，可以看出吸振球确实在θ=0附近作微小振动。

图5 吸振球的实际振幅变化规律Fig.5 The variation laws of actual amplitude curve of ball damper

2 动力吸振器参数的优化设计

在主振系参数一定的条件下，吸振球的质量m（或μ）对主振系振幅的影响见图6所示，μ越大制振效果越好，但实际μ的选取要根据主振系的质量M，综合考虑系统总质量与主振系的振幅降低程度来确定。

在μ值确定之后，为了能使主振系的振幅在较大频率范围内尽可能降低，利用定点的性质，吸振球的其余参数η，ξ（或R－r，cb）可以按以下条件进行优化设计。

图6 吸振球质量对主振系振幅的影响Fig.6 The effects of the mass of ball damper on the amplitude curves of main vibration system

2.1 最优频率比

为了使两定点P，Q的振幅尽量降低以调整参数η。当η改变时，根据式（10）和式（11），一个定点的振幅下降，同时另一个定点的振幅上升，如图7所示。因此，为了能在较大频率范围内尽可能降低主振系的振幅，使定点P，Q的振幅相等，以调整η（或p）值。

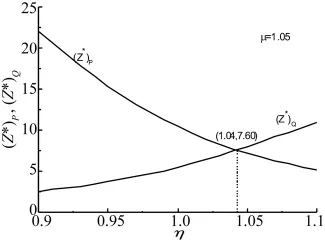
图7 两定点P和Q振幅的变化规律Fig.7 The variation laws of amplitude curves of fixed points P and Q

令λP，λQ点的振幅相等，由式（11）得：

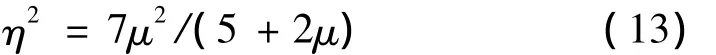
将式（13）代入式（10），得此时两个定点的频率值为：

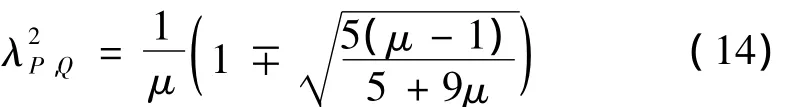
此时，两个定点的振幅为：

2.2 最优阻尼比ξ

在满足最佳频率比条件式（13）的基础上，再使定点P，Q处的振幅Z*达到极大值，以确定最优阻尼比ξ值。即在频率比由式（14）确定的定点处使∂Z*/∂λ=0。因式（8）是λ2的函数，所以该极大值条件可以等价为：

为了简化上式的计算，将式（8）变形为：

其中：

将式（17）代入式（16），得：

由于定点的振幅与ξ无关，所以式（19）中的N/D可以用式（11）替换，得：

由式（18）计算出各偏导数后代入式（20），考虑式（10）、式（13）和式（14），得：

其中：

由式（21）和式（22）知ξP≠ξQ，即无论如何调整ξ都不能使定点P和Q的振幅同时达到极大值，作为近似可选用其平均值作为最优阻尼比，即：

图8 参数优化后主振系的振幅Fig.8 The optimized amplitude curve of main vibration system

经过以上最佳参数调整后主振系的振幅如图8所示，吸振球的实际振幅见图9所示。

3 双方向吸振问题

图9 参数优化后吸振球的实际振幅Fig.9 The optimized actual amplitude curve of ball damper

根据前面的研究结果，该吸振器能够在一定的频率范围内有效地控制单方向的简谐振动（见图8）。但当机械或结构承受两个正交方向的简谐振动时，根据二维简谐振动的合成原理［8］，只有在两个方向振动是同频率，且相位差是0或±π时，合成振动是同频率的直线简谐振动，这时同样能够进行有效地控制。

4 结论

本文提出了一种结构简单的滚珠式动力吸振器，通过滚珠在凹球面内的运动，可以控制机械或结构的特殊的多方向振动，并通过理论分析、数值计算和参数优化设计，确认了该吸振器可以大幅度降低强迫振动响应，具有优良的振动控制性能。

［1］刘耀宗，郁殿龙，赵宏刚，等.被动式动力吸振技术研究进展［J］.机械工程学报，2007，43（3）：14－21.

［2］松久寛.動吸振器の制振効率と最近の動向.日本機械学会講演論文集［C］，2004，41－44.

［3］佐藤久雄，千島美智男.索道用二球転動式動揺減衰装置の調整方法とその効果［C］.日本機械学会論文集，2007，73（730）：105－116.

［4］松久寛，顧栄栄，王永金，ほか2名.索道搬器の動吸振器による制振［C］.日本機械学会論文集，1993，59（562）：115－120.

［5］荒川利治，古平有一，大亦絢一郎.半円弧ばねと磁気減衰を用いた動吸振器の研究［C］.日本機械学会論文集，2007，73（732）：23 －29.

［6］张小龙，东亚斌.双滚珠自动抑制转子主共振的机理（线性支承刚度）［J］.西安建筑科技大学学报，2009，41（2）：282－287.

［7］张小龙，东亚斌.滚珠自动控制转子不平衡响应的动力学机理［J］.机械工程学报，2009，45（7）：95－100.

［8］ French A P.Vibrations and waves（The M.I.T.Introductory Physics Series）.W.W.Norton ＆ Company，1971.