PDE信号修补方法及在EMD端点效应处理中的应用

尹爱军，王 璇

（重庆大学 机械传动国家重点实验室，重庆大学 机械学院测试中心，重庆 400044）

PDE是一个含有多元未知数函数及其偏导数的方程。PDE是在讨论自然现象（特别是物理现象）的过程中逐步建立起来的，所以也称为数学物理方程。PDE最新的研究与应用已扩展到经济、金融预测、图像处理、振动信号处理等领域［1－4］。

二阶线性PDE是偏微分方程理论中较为成熟的部分，并成为其他分支借鉴的典范。热传导方程见式（1）是最简单、最基础的抛物型PDE，可用于描述热传导、扩散等物理现象，得到了非常广泛的应用。

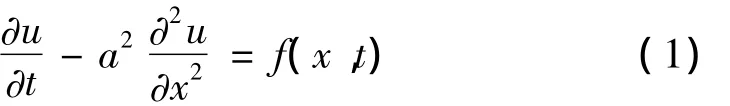
热传导方程初值问题的解实际上就是一个高斯滤波器，即当f（x，t）=0时，利用傅立叶积分法可得式（1）的解为：

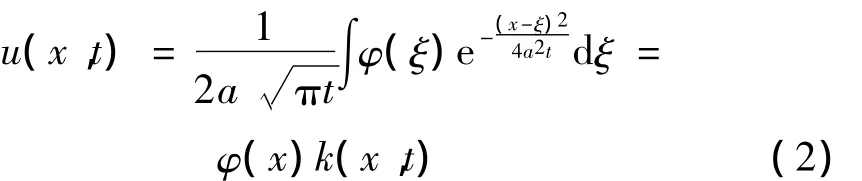
其中，

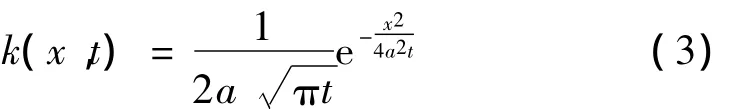
因此，热传导方程在信号滤波降噪中得到了广泛应用，特别是在二维图像信号的滤波降噪中。

Hilbert－Huang变换是由 Huang等［5］提出的一种新的非平稳信号分析方法。HHT包含两个过程：首先对信号进行非线性的自适应分解，称为经验模态分解（Empirical Mode Decomposition，EMD），它把复杂信号分解成有限个本征模态函数（Intrinsic Mode Function，IMF）之和；然后对各个IMF进行Hilbert变换，研究信号的时频能量分布。

如果定义y（t）为原信号序列，imf（t）为经EMD得到的本征模态函数（IMF），r（t）为余量，则原始信号可以表示为所有的IMF及余量之和：

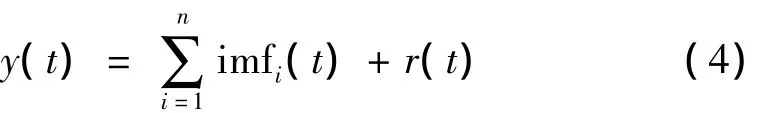
对于每一个IMF，应满足：① 在整个数据段内，极值点的个数和零交叉点的个数必须相等或相差最多不能超过一个。② 在任何一点，由局部极大值点形成的包络线和由局部极小值点形成的包络线的平均值为零。

HHT分析的核心是EMD分解。EMD分解过程中，每一个IMF都需要多次筛选过程来实现，而每一次筛选过程必须找到局部极大值构成的上包络和局部极小值构成的下包络，并用三次样条插值来分别计算出上下包络的插值及其平均值。由于信号的端点一般不会同时是局部极值点，因此利用EMD进行分解时，因包络线不准确会引起误差，并且这种误差会随着IMF分解层数的增加而向内传播，继而“污染”整个数据序列，使得最后的分解结果失去意义。为此，众多研究人员相继提出了相关的端点处理方法［6］，如端点镜像外延［7］、多项式外延［8］、神经网络处理［9］、支持向量机预测［10］、相似极值延拓［11］等方法。另有研究人员则根据EMD方法的基本思想，提出了局部均值分解改进方法［12］。

本文针对振动信号的内在性质，分析基于插补等方法的信号修补方法，提出了PDE信号修补新方法，并将这一方法成功用于EMD分解过程中的端点效应处理。

1 基于PDE的波动信号修补

1.1 信号修补方法

对于数字信号分析系统来讲，在将模拟信号转换为数字信号的过程中，总会存在各种各样的干扰，或者硬件设备本身的性能指标等因素，使得数字信号可能会存在失真。如采样频率太高，而分析系统处理速度过慢，从而引起的分析信号不连续、数据掉点等等。如图1所示，图1（a）是理想信号，图1（b）表示了信号不连续情况。因此，需要对这一类信号进行修补，复原信号。

对于一个一般实际系统，总可以将其表示为如式（5）所示的系统形式。实际系统内部一般存在储能元件和耗能元件，因此系统的输出具有连续性，或者局部光滑性。利用这一特点，我们可以设计多种修补方式。

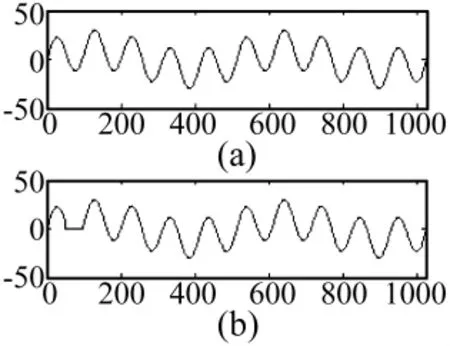
图1 原始信号与缺陷信号Fig.1 Original signal and distortion signal

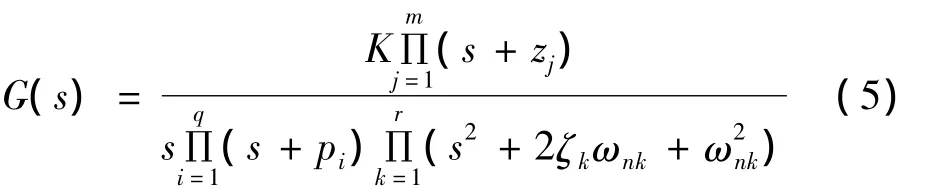
拉格朗日插值、牛顿插值、埃尔米特插值、样条插值等方法即是利用实际信号的连续性和光滑性所实现的典型信号修补方法。式（6）为拉格朗日多项式插值表达式。显然，若数据量小，缺陷信号的时间很短，则可以直接利用中值插值、线性插值等方法。

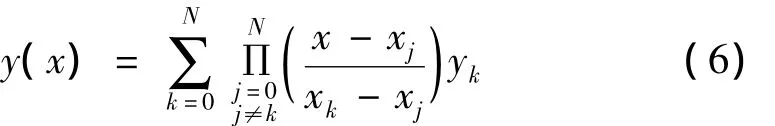
1.2 PDE信号修补原理

热传导方程表示了一种传热过程（或者扩散过程），且这种传导过程是连续光滑的。并且我们注意到，热传导方程初值问题的解就是一个高斯滤波器。因此，对于上述畸变信号同样可以用PDE方法进行修补。

为简化计算过程，令式（1）中f（x，t）=0，a=1，即有：

设原始振动信号为y0（x），畸变信号位置范围为［x1，x2］，于是可以得到如下修补公式：

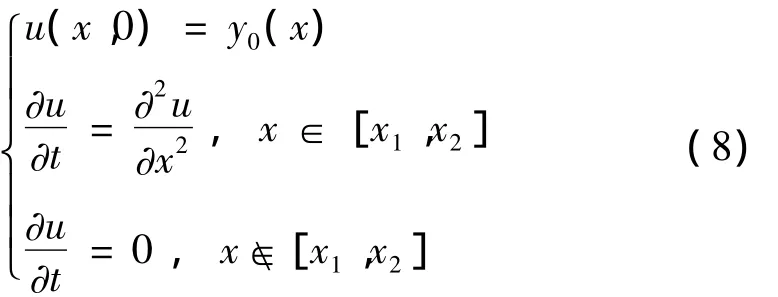
即对于畸变缺陷信号，根据热传导过程中的连续及光滑性，逐渐重构出原始信号；而对于正常信号，则不作处理。

式（8）是直接根据高斯滤波实现的线性PDE修补方法，这一方法没有考虑信号之间的变化，从而可能会影响修补信号的瞬态特性。为此，可以采用式（8）的非线性 PDE 修补方式［1，13－14］。

其中k（·）表示一个特定函数，如：

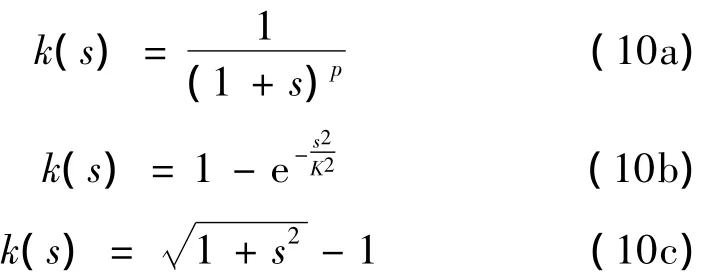
其中p、K为调制系数。grad（·）为梯度函数，典型的有前向差分［式（11a）］、后向差分［式（11b）］、中心差分［式（11c）］等。

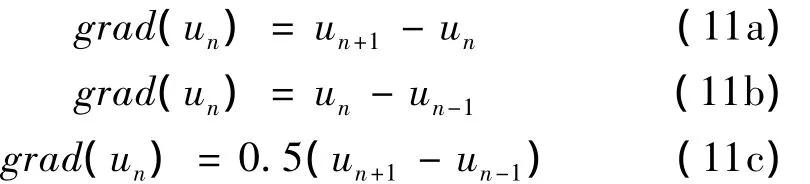
在这一修补方式下，可以针对信号梯度设置相应的调制参数，使修补后的信号即满足整体连续光滑、又满足瞬态冲击特性。

若定义如下模板函数：

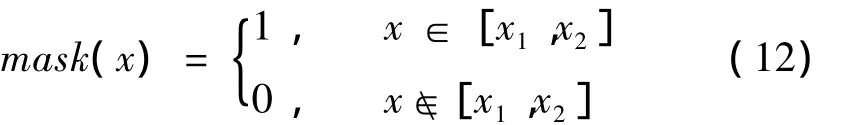
x1，x2表示修补范围。则式（9）可以表示为：

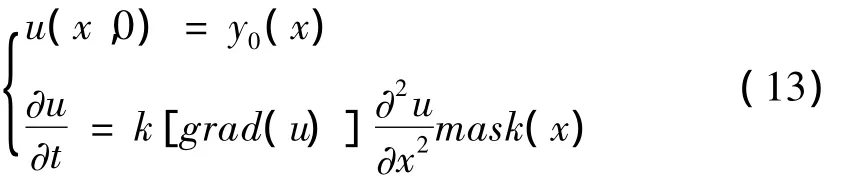
1.3 仿真试验

设由两个正弦信号组成的理想信号，如式（14）。设置采样频率为1 000 Hz，取连续1 024个数据点（y1，y2，…，y1024），如图 1（a）所示。畸变信号为y50，y51，…，y100，如图 1（b）所示。

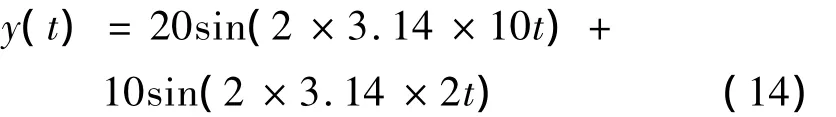
图2（a）为拉格朗日多项式插值修补效果；图 2（b）为三次样条插值修补效果；图2（c）为采用式（8）所示的线性PDE修补效果；图 2（d）为采用式（9）所示的非线性PDE修补效果。其中式（8）、式（9）的迭代次数均为1 000次。对于非线性 PDE修补，选择式［10（a）］作为调制函数，并令p=－0.01，梯度函数为式（11a）。从图可以看出，上述方法均可实现信号的修补，非线性PDE因考虑了信号内部梯度，修补效果比线性PDE好。

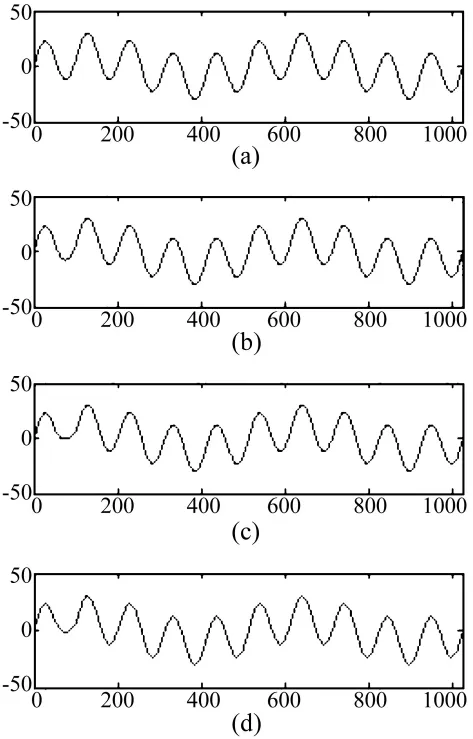
图2 信号修补Fig.2 Signal restored

2 EMD端点效应的PDE处理

2.1 PDE端点效应处理

实际上，上述所提到的这些方法，都是利用信号的连续性（样条修补、多项式等）、相似性（镜像、周期延拓等）等特征，根据已有信号两端的性质，实施的信号修补方法。也就是说，我们需要利用信号的一端特性，恢复出原始信号。相对于前面讨论的信号中间修补方法，显然这里的修补条件要“弱”。

同样，我们可以利用PDE的信号修补性质，实现信号的端点扩展处理。此时，只需要定义模板函数式（12）的延托范围即可。假定原来信号长度为L0，延托之后信号长度为L1，定义：

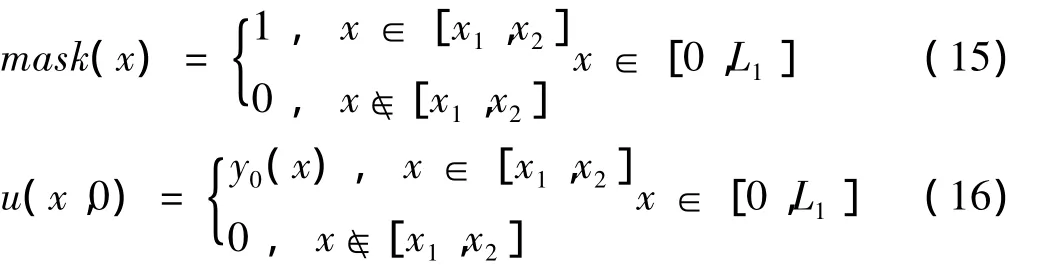
其中，L0=x2－x1，即实现在原始信号左右两端同时扩展，左端扩展长度为Ll=x1，右端扩展长度为Lr=L1－x2。

2.2 试验分析

对式（14）所示的模拟信号，如图1（a），令其左右两端各50个数据为0，如图3所示。图4－图8分别表示理想模拟信号［图1（a）］的 EMD分解结果，及利用不同扩展方法恢复出左右各50个数据后的EMD分析结果。EMD算法为Rilling等［7］提出的改进算法。为便于观察和比较，图中同时给出了信号两端的扩展数据波形。图9为式（13）实现的非线性PDE扩展及其分解，其中调制函数为式（10a），p=－0.01，梯度函数为式（11a），迭代次数为1 000。

由图可以看出，端点扩展是信号修补的一种形式，因此关于信号修补的方法同样适用于端点扩展。但因在扩展时，只有一端的特征信息可以利用，因此，常规的信号修补（扩展）方法完成扩展后，两端畸变大，如图5～图8。图8所示SVM扩展方法，采用多项式核函数，多项式次数为5。实际上，SVM扩展方法很不理想，本文试验了多种核函数，均无法获得较好的扩展效果。对于传统方法，当扩展信号较长时，畸变更为明显。非线性PDE扩展端点畸变少，且适用于较长数据的扩展。PDE扩展之后的分解结果与理想边界信号分解结果一致。

图10为一数控车床电主轴低速状态下的测试振动信号利用非线性PDE端点处理后的EMD分解结果。由图可以看出，端点处理较好的保证了EMD分解的有效性，没有存在发散等现象。限于篇幅，本文没有给出其他端点扩展方式下的EMD分解结果。

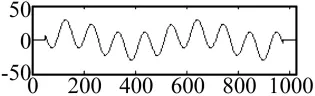
图3 端点扩展模拟信号Fig.3 Analog signal for extending end

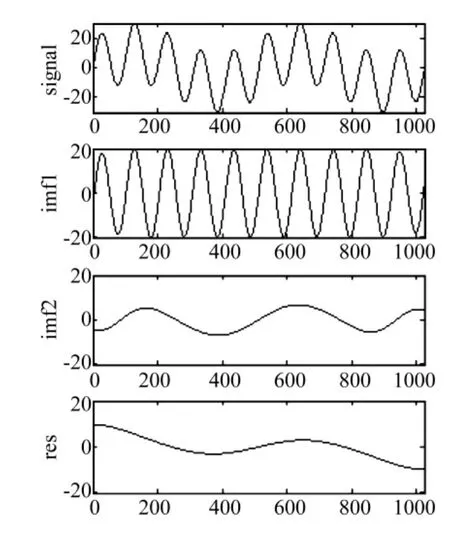
图4 理想边界EMD分解Fig.4 EMD decomposition based on ideal end

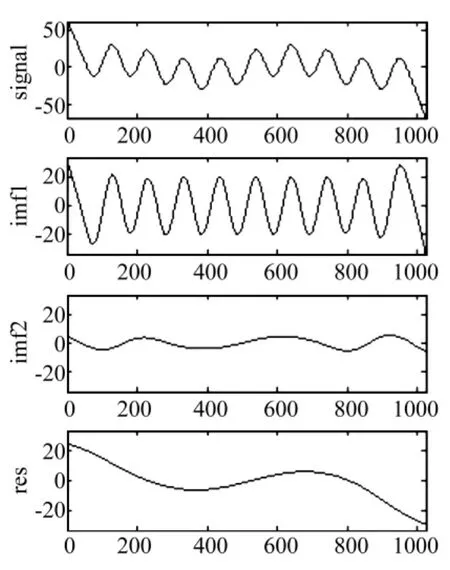
图5 抛物线扩展EMD分解Fig.5 EMD decomposition based on extending end using parabola

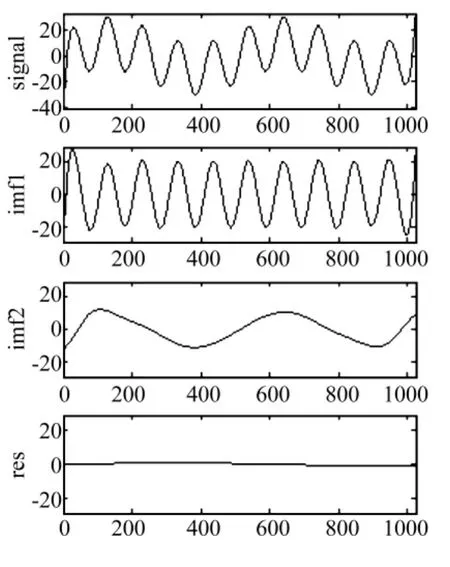
图6 拉格朗日多项式扩展EMD分解Fig.6 EMD decomposition based on extending end using lagrange polynomial

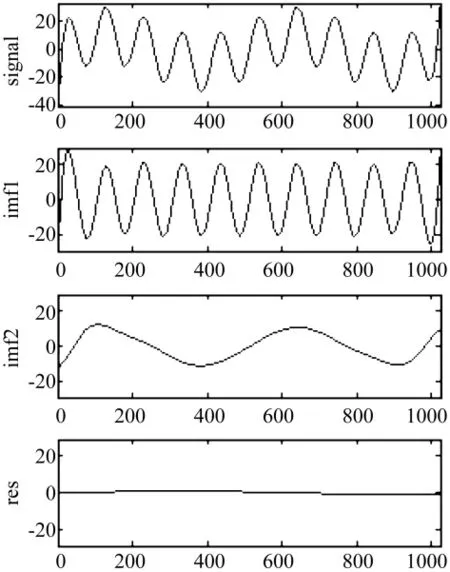
图7 三次样条扩展EMD分解Fig.7 EMD decomposition based on extending end using cubic spline

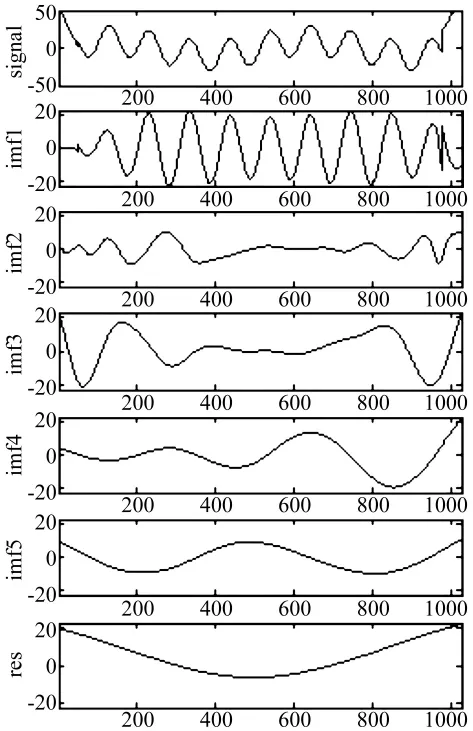
图8 SVM扩展EMD分解Fig.8 EMD decomposition based on extending end using SVM

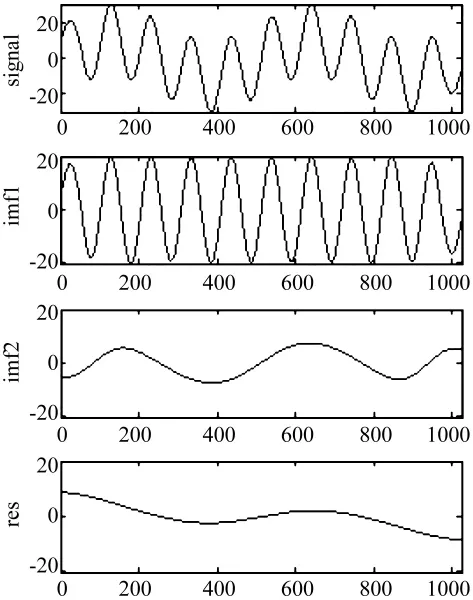
图9 非线性PDE扩展EMD分解Fig.9 EMD decomposition based on extending end using nonlinear PDE

3 结论

根据振动信号的局部连续性、光滑性特性，可以根据已有信号实现对缺陷信号的修补。三次样条修补、多项式修补等方法实际上就是依据这一原理。热传导方程反映了热传导这一过程中的连续性、光滑性等特点，其初值问题的解即为一个高斯滤波过程，因此热传导方程可以用于信号的修补。非线性PDE信号修补时，同时还兼顾了信号之间的梯度特征，因此修补后既能保证信号的连续、光滑性，还能保持其瞬态性。

EMD方法是一种新的非平稳信号分析方法。EMD方法把复杂信号分解成有限个IMF之和，而这一分解过程中，信号端点的处理是其关键问题之一，直接影响到分解的有效性。常用的端点处理方法实际上就是一种信号的修补方法。但是在端点扩展处理时，只能考虑一端对“缺陷”信号的影响，因此利用常用方法处理之后，端点会存在较大的畸变，并且随着扩展信号长度的增加，畸变越来越大。PDE信号端点扩展方法是一种新的端点处理方法，可扩展复原出较长时间长度的信号，且处理之后的信号畸变少。

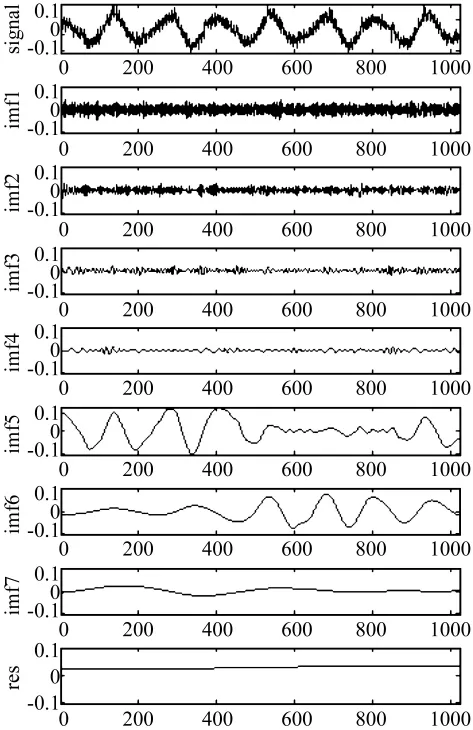
图10 实际信号PDE扩展的EMD分解Fig.10 EMD decomposition of real signal based on extending end using PDE

PDE方法可完成信号的修补，但在这一过程中，仍有一些问题需要进一步研究。如怎样确定PDE修补过程的迭代次数、怎样选择或者设计调制函数、怎样确定调制函数的参数等问题。

［1］ Tschumperle D，Deriche R.PDE’s based regularization of multi-valued images and applications［J］.IEEE Trans on Pattern Analysis Machine Intelligence，2005 ，27（4）：506－517.

［2］Rudin L，Osher S，Fatemi E.Nonlinear total variation based noise removal algorithms［J］.Physica D，1992，60（1 －4）：259－268.

［3］ Weickert J.A review of nonlinear diffusion filtering［J］.Scale-Space Theory in Computer Vision，Lecture Notes in Computer Science，Berlin，1997，1252：3 －28.

［4］吴宏钢，尹爱军，秦树人.基于PDE的振动信号去噪［J］.机械工程学报，2009，45（5）：91 －94.

［5］Huang N E，Shen Z，Long S R，et al.The empirical mode decomposition and the Hilbert spectrum for nonlinear and nonstationary time series analysis［J］.Proc.R.Soc.Lond.A，1998，454：903－995.

［6］胡维平，莫家玲，龚英姬，等.经验模态分解中多种边界处理方法的比较研究［J］.电子与信息学报，2007，29（6）：1394－1398.

［7］Rilling G，Flandrin P，Goncalyes P.On empirical mode decomposition and its algorithms［C］.IEEE-EURASIP Workshop on Nonlinear Signaland Image Processing（NSIP2003），Grado（I），June，2003：8 －11.

［8］刘慧婷，张 旻，程家兴.基于多项式拟合算法的EMD端点问题的处理［J］.计算机工程与应用，2004，40（16）：84－86.

［9］邓拥军，王 伟，钱成春，等.EMD方法及Hilbert变换中边界问题的处理［J］.科学通报，2001，46（3）：257－263.

［10］程军圣，于德介，杨 宇.基于支持矢量回归机的Hilbert_Huang变换端点效应问题的处理方法［J］.机械工程学报，2006，42（4）：23 －31.

［11］沈 路，周晓军，张志刚，等.Hilbert-Huang变换中的一种端点延拓方法［J］.振动与冲击，2009，28（8）：168－171，174.

［12］程军圣，张 亢，杨 宇，等.局部均值分解与经验模式分解的对比研究［J］.振动与冲击，2009，28（5）：13 －16.

［13］ Tschumperle D.PDE's based regularization of multivalued images and applications［D］.Antipolis：University of Nice-Sophia，2002.

［14］ Tschumperl D.Fast Anisotropic smoothing of multi-valued images using curvature-preserving PDE's.International Journal of Computer Vision，2006，68（1）：65－82.