轮胎自激振动分岔参数影响分析

杨宪武，左曙光，雷 镭，吴旭东，李 勇

（同济大学 汽车学院，上海 201804）

随着高速公路的普及，汽车行驶在高速公路上的时间越来越长，随之而来的自激多边形磨损现象经常在汽车轮胎上发生。这种磨损可导致轮胎提前报废，造成爆胎等严重威胁汽车行驶安全的事故，严重影响到产品和企业的形象。这种不均匀磨损的潜在原因很多，可能是车辆的动态性能、定位参数、悬架和道路情况等方面的原因，也可能是轮胎的结构参数、形状参数、胎面形式和胎压等原因造成的。

国内外，对于轮胎偏磨损机理的研究，集中了大量的精力来研究轮胎与路面之间相互作用的微观和宏观机理，并以此来试图解释轮胎磨损的各种形式［1－4］，但目前尚无成熟的理论方法。日本Atsuo Sueoka［5］研究小组将两接触旋转轮滚动之间可以产生自激振动的原理在汽车轮胎周向多边形磨损机理研究中，较成功地解释了多边形磨损的现象，但模型中没有考虑前束角的影响，且只研究了垂向一个自由度，故不能合理地应用到汽车轮胎磨损研究中。本文正是基于这样的背景，结合同济大学汽车学院轮胎多边形磨损科研小组前期研究成果［6－7］，从轮胎与路面之间的相互作用机理入手，在侧向方面探讨了轮胎的自激振动，研究自激振动发生分岔的车速范围和自激励系统振动特性及车速的关系，以及前束角、胎面质量块和载荷变化等因素对自激励系统振动的影响。

1 胎面－路面摩擦模型

1.1 摩擦系数曲线的选取

在胎面－路面模型中，摩擦特性的描述一直是轮胎力学建模的重点和难点，它直接关系到模型的精度。摩擦系数分为动摩擦系数和静摩擦系数，两者之间摩擦状态的切换是轮胎摩擦特性中比较难以建模的问题，而摩擦状态的切换又是汽车使用中经常会遇到的工况。过分简单的数学模型不能正确描述摩擦力的变化规律，采用复杂的数学模型又不能得到系统运动过程的解析结果，因此，建立合理的数学模型是研究摩擦力激励自激的一项关键任务。

以往轮胎模型中摩擦系数多假设为常数，或仅给出摩擦系数随速度变化而简单下降的经验公式［8］。而通过对轮胎橡胶块摩擦试验可以看到橡胶的摩擦系数随滑移速度增加是先上升后下降，下降趋势是先急剧后缓和［9］。

库伦摩擦是最早被发现的一种摩擦现象，随着对摩擦现象的不断认识，结合面间的粘滑摩擦被逐渐重视起来。滚动轮胎接地面上的摩擦力主要包括两个分力：粘附摩擦力和滞后摩擦力。前者为两对摩表面摩擦力，而后者则是周期性变形引起并产生于轮胎本身的基体摩擦阻力［10］。图1给出了两者间相对速度大小与粘滑状态之间的关系图［11］。

后来Stribeck模型，指数模型，Karnopp模型，鬃毛模型均对动静摩擦系数之间的转换进行了深入的分析，Canudas de wit［12］提出了一种更加完善的 Lugre 模型，该模型是鬃毛模型的扩展，同时采纳了鬃毛模型的思想，即在微观下接触表面可以看成是大量的具有随机行为的弹性鬃毛。但鬃毛模型描述的是摩擦的随机行为，而LuGre摩擦模型则是基于鬃毛的平均变形来建模，综合考虑了两者接触面间的粘附摩擦，迟滞特性以及激励频率对迟滞环的影响，其模型表达式如式（1）所示：

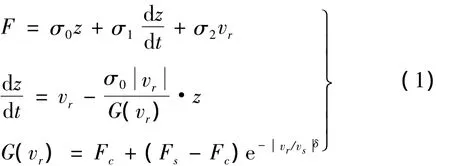
式中：σ0为刷毛刚度系数；σ1为刷毛阻尼系数；σ2为相对粘滞阻尼系数；z为刷毛的平均弹性变形量；vr为两接触物体间的相对速度；vs为Stribeck速度；δ为Stribeck指数（一般取0.6～2）；Fs为最大静摩擦力；Fc为滑动摩擦力；F为总摩擦力。

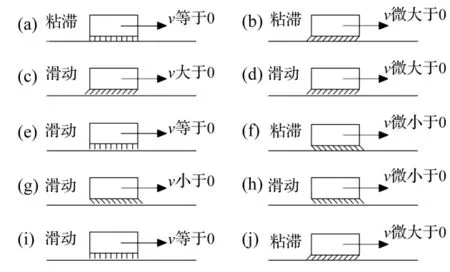
图1 相对速度与粘滑状态关系图Fig.1 Relationship between relative velocity and stick-slip state

如图2所示，当相对速度的变化频率较低时，Lugre模型表现出与稳态摩擦模型相一致的静态摩擦特性，随着输入频率的不断提高，Lugre模型的动态迟滞特性愈发明显，说明Lugre摩擦模型可以根据接触面间相对速度vr的不同变化做自我调整，表现出不同的摩擦特性，而轮胎接地印迹块在汽车前进过程中表现出明显的弹性迟滞特性，因此，Lugre摩擦模型可以很好地模拟汽车轮胎与地面间摩擦行为的瞬态特性。

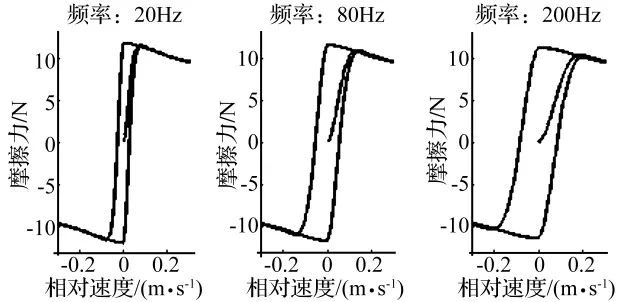
图2 不同输入频率下的Lugre摩擦特性曲线Fig.2 Friction curve of Lugre model with different input frequency

1.2 模型构建

除了空气作用力外，汽车运动所需的所有外力都是由车轮和路面之间的相互作用产生的，因而轮胎力学特性与汽车动力学特性密切相关。为了准确地描述轮胎的动力学特性，将车轮分成两部分来建模：轮辋和轮胎等效接地印迹块。轮辋看成刚体，与轮胎接地印迹块之间通过弹簧和阻尼器进行连接，其中弹簧和阻尼器代表胎体本身的弹性特性。

轮胎力是它与路面间的切向约束力，就物理性质而言，属于摩擦力的范畴，但其变化规律与系统运动状态有关，并不简单取决于摩擦定律。后者只能确定轮胎力的最大值和相关速度的关系。为了查清路面给轮胎约束力的影响因素，按照解除约束代之以约束力的通用的力学分析方法，将车轮从车辆上分离出来。

将胎面离散化为若干集中质量块，假设各质量块沿轮胎宽度方向振动，且在相邻质量块间存在着弹簧和阻尼的作用。取其中任一质量块作为研究对象，其与整个轮胎的连接方式如图3所示。汽车前进方向为垂直纸面向里。

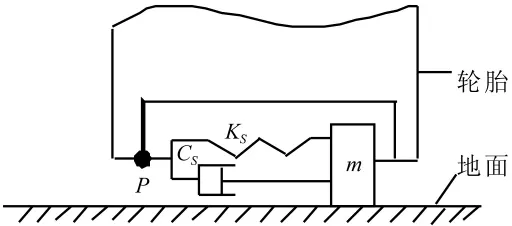
图3 胎面质量块与轮胎连接示意图Fig.3 The connection between tread and tire

在模型中，振动能量的输入来源于胎面与地面之间持续不断的摩擦力作用，即两者之间的相对速度变化是激励源。为便于分析，将轮胎与地面间的平动速度Vb简化为皮带轮的转动。

其中：

v为汽车行驶速度，θ为车轮前束角。

简化后的模型如图4所示，m为离散的胎面质量块，Ks和Cs分别为弹簧刚度及阻尼系数。

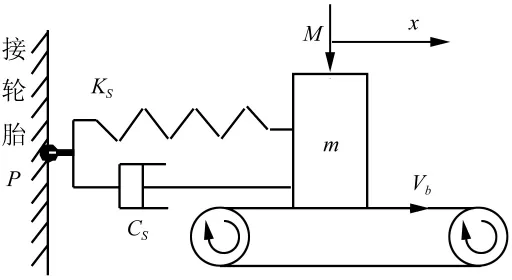
图4 胎面质量块摩擦模型Fig.4 Friction model of tread

设胎面质量块m在皮带上相对于初始位置的位移为x，则质量块与皮带之间的相对速度为：

根据牛顿－欧拉运动学方程，可以列出胎面质量块m侧向滑移的动力学方程如下：

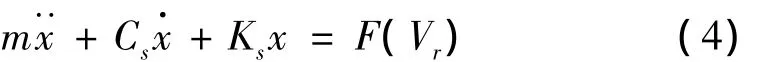
其中M为汽车轮载荷在胎面质量块m上的分布压力，F（Vr）为随相对速度变化的摩擦力曲线，将Lugre摩擦模型代入可得：

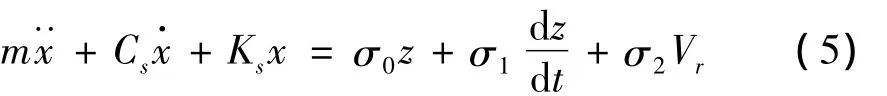
2 自激振动的产生机理

自激振动系统中存在着非线性阻尼的作用，这种非线性阻尼有着特殊和非常重要的性质：对于较小的速度有使振幅增加的趋势，是负阻尼作用；对于较大的速度，又有使振幅减少的倾向，是正阻尼作用，系统以自己的运动状态为调节器，使输入的能量具有交变性。当输入的能量与耗散的能量达到平衡时，系统可以维持等幅振动，称为自激振动，它的相轨迹为相平面内孤立的封闭曲线稳定，微分方程几何理论称之为极限环［13］。

极限环分为稳定极限环和不稳定极限环，考虑到真实的动力学系统要承受外界扰动，不稳定的周期运动不能保持。因此，自激振动的相轨迹必须是稳定的极限环。

将式（4）右侧摩擦力进行一阶泰勒展开得：

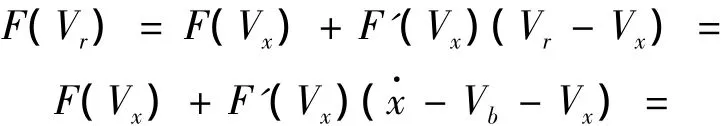
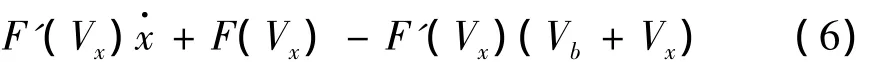
将式（6）代入式（4），略去与振动无关的常数项并整理，得到在物体与皮带轮之间的相对速度v=vx时的瞬时振动微分方程：

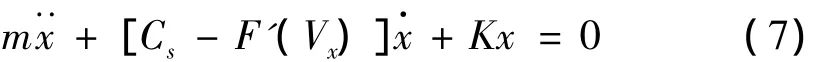
此时，该振动系统的当量阻尼为：

当Ce＞0，即Cs＞F'（Vx）时，该振动系统处于“正阻尼”状态，系统的能量被损耗，振动有衰减趋势；当Ce=0，即Cs=F'（Vx）时，该振动系统处于“无阻尼”状态，系统的总能量不变，维持等幅振动；当Ce＜0，即Cs＜F'（Vx）时，该振动系统处于“负阻尼”状态，系统从外界吸收能量，振动有增强的趋势。

图5所示为摩擦力从静摩擦到动摩擦的变化走势图，其中fs，fc分别为最大静摩擦力和刚刚发生完全滑动时的滑动摩擦力，V1，V2分别为对应于fs，fc的相对速度。当v∈［0，v1］时，两个接触面处于粘滞状态，摩擦力属于静摩擦，其大小与相对滑动速度基本呈线性关系且斜率很大。在v=v1处，f达到最大值fs，即为最大静摩擦力；当v∈［v1，v2］时，接触面的部分质量开始出现滑动，于是两个接触面处于部分粘滞状态，摩擦力逐渐从静摩擦过渡到滑动摩擦。由于滑动摩擦力小于最大静摩擦力，因此这一部分的曲线斜率为负值。当相对速度在v1两侧来回变化时，就有可能使得Ce在正负之间逐次交替，从而让振动系统在消耗能量和吸收能量之间找到一个平衡状态，达到稳定的自激振动。

综上所述，对于干摩擦振动系统，其摩擦特征曲线中的“负斜率”部分是形成自激振动的根本原因。若此“负斜率”部分足以抵消振动系统自身的“正阻尼”，则该振动系统便会表现出整体“负阻尼”状态，进而产生自激振动；而若摩擦特征曲线的“负斜率”特征不明显，或者振动系统自身的“正阻尼”比较大，则该振动系统无法出现整体“负阻尼”状态，振动将被衰减，因此无法形成自激振动

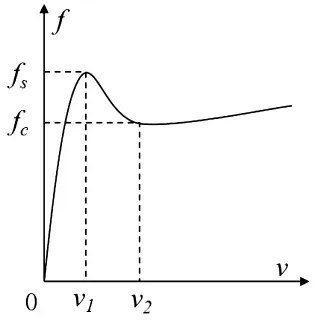
图5 摩擦力特征曲线Fig.5 Characteristic curve friction force

3 分岔点的计算

动力系统的分岔现象是指随着某些参数的变化，系统的动态行为发生质的改变，特别是系统的平衡状态发生稳定性改变或出现方程解的轨道分歧。因此找出状态发生改变的参数点对于动力系统的稳定性控制有着极其重要的作用。

3.1 模型的线性化

非线性系统的稳定性研究比较困难，没有普遍的分析解法，要依靠数值解法。但Lyapunov的一次近似定理证明［14］，在小扰动下，由线性化模型得到的关于稳定性的结论，除了临界点附近的情况以外，可以适用于真实的非线性系统。

胎面质量的非线性动力学方程（1）可用状态方程表示为：

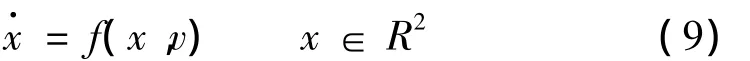
式中v为车辆行驶速度，是一个动参数，x为状态变量。令x0为方程（2）的平衡点，则非线性动力系统式可以改写成线性部分与非线性部分分开的形式：

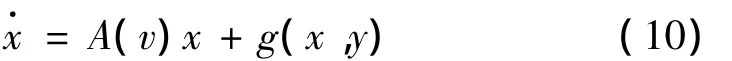
式中g（x，y）在平衡点x0的邻域内是x的高阶无穷小量，A（v）是函数f（x，y）在平衡点x0处的 Jacobian矩阵，其表达式为：

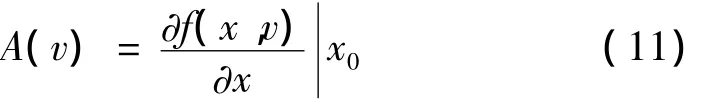
3.2 极限环的存在性及稳定性分析

用Hopf定理证明极限环的存在性时，分岔点的寻找，一般是通过计算Jacobian矩阵A（v）的所有特征值来判断是否有特征根穿越虚轴［15］。这种方法需要对每一车速计算所有特征根并判定根的实部是否为零，计算量很大。尤其当状态方程的构成较为复杂时，很难写出特征根的解析表达式。而利用Hurwitz行列式，可以将分岔点的求解转化为一个非线性方程的求解，从而克服了以前方法在计算Hopf分岔点时，对于参数的每一次变化通过求特征根并判定特征根的实部是否为零的庞大工作量［16］。

对方程（5）进行线性化后的Jacobian行列式为：

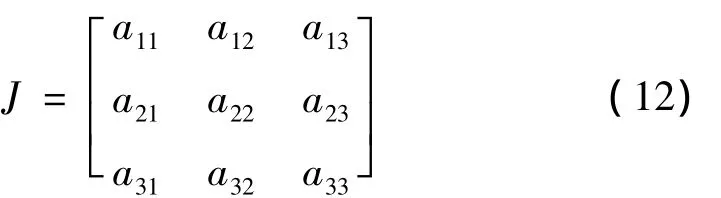
其中：

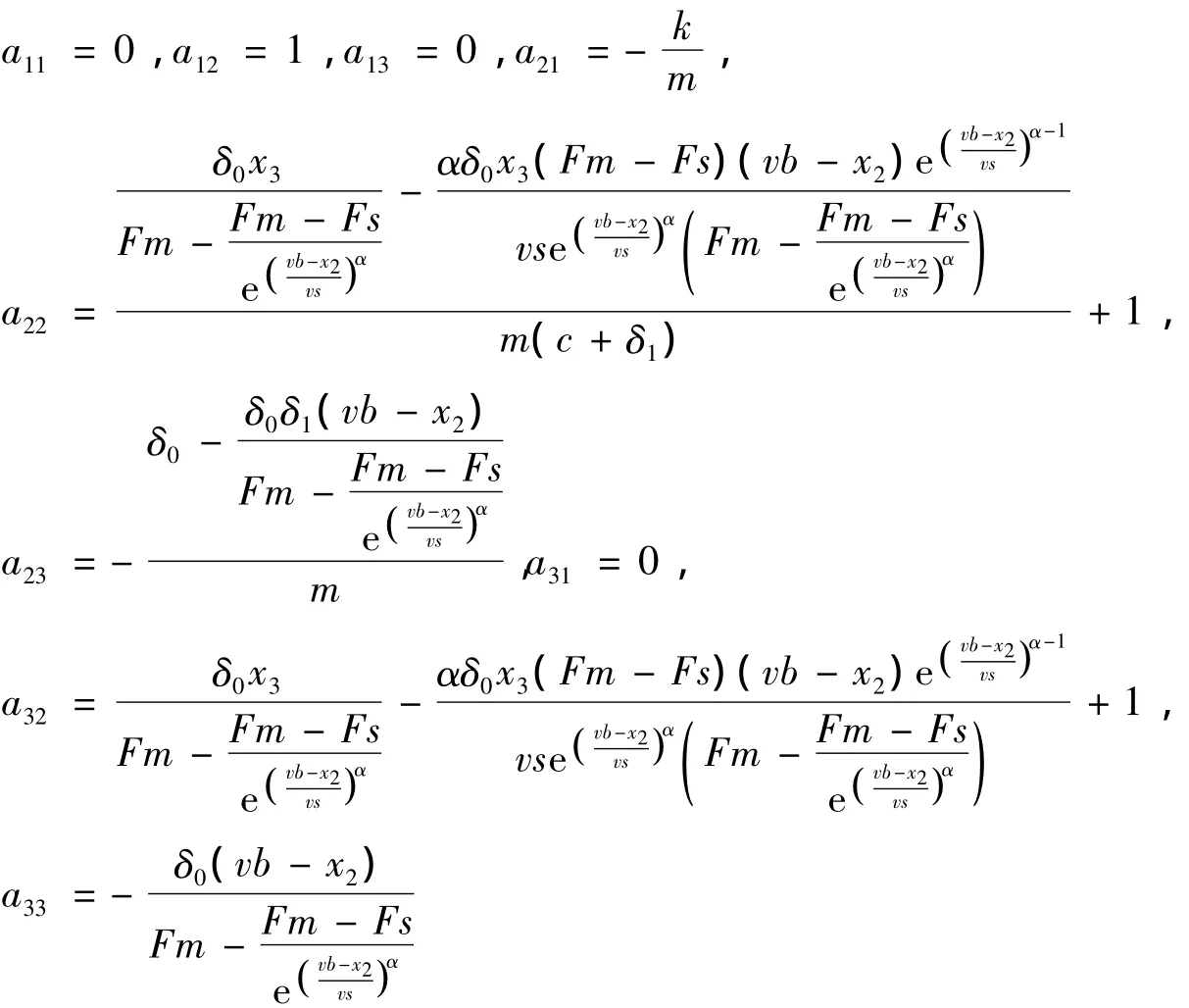
式（12）的特征多项式为：

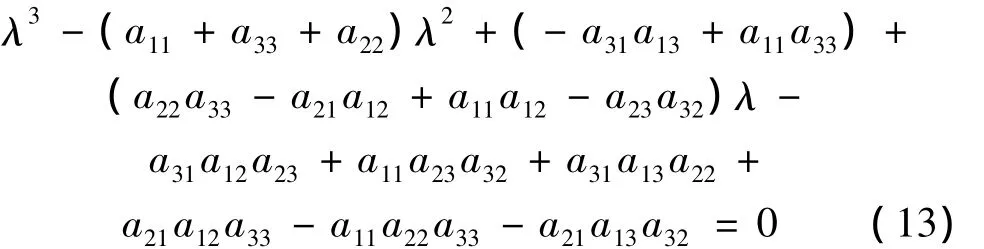
通过式（13）的系数可以写出Hurwitz行列式，进而计算出当Vb=0.144 649和Vb=0.172 816时，即当车速为v1=99.5 km/h和v2=118.8 km/h时，方程（13）有一对纯虚根，根据参考文献［17］知，非线性系统方程式（5）在车速为v1=99.5 km/h处发生了Hopf分岔，车速在超过99.5 km/h时，系统的平衡点不再是稳定的，出现了极限环振动现象，当车速达到v2=118.8 km/h时，系统再次发生了Hopf分岔，极限环振动逐渐消失，是一种典型的硬自激振动。

由上面分析可知：速度v1、v2为系统的分叉点，对应此速度的轮胎运动状态会突然发生变化。当速度超过v1、v2后，可能会出现超临界分岔，对应稳定的周期振动，即存在稳定的极限环；也有可能会出现指数发散的亚临界分岔，即存在不稳定的极限环。可通过判断最大Lyapunov指数的正负来判定极限环的稳定性。

Lyapunov指数定量地描述了相空间中相邻轨道呈指数发散的性质。若L指数＜0，表示相体积收缩运动稳定，且对初始值不敏感；若L指数=0，则对应临界状态，即稳定的边界；若L指数＞0，表示相轨道分散，长时间行为对初始值非常敏感，运动呈现混沌状态。

通过计算得知，在车速v1=99.5 km/h处系统发生分岔时对应的 Lyapunov指数为 －757.703 1，在车速v2=118.8 km/h处系统发生分岔时对应的Lyapnov指数为－568.950 4，这说明在临界速度v1、v2处发生的Hopf分岔均为超临界分岔，所产生的极限环都是稳定的，即轮胎胎面将沿侧向做稳定的自激振动。

4 仿真结果与分析

为研究汽车动态特性及定位参数等对轮胎自激振动的影响，以国内某一典型车辆作为研究对象，在matlab软件中建立simulink模型，图6给出了胎面块位移随速度变化的分岔图。从图中得知，当速度在99.5 km/h之下时，胎面块没有出现自激振动，处于稳定状态，而当速度在［99.5，118.8］km/h 之间变化时，胎面出现稳定的自激振动，且振幅先增大后减小，当速度大于v2=118.8 km/h时，胎面再次出现渐近稳定状态，自激振动现象消失。

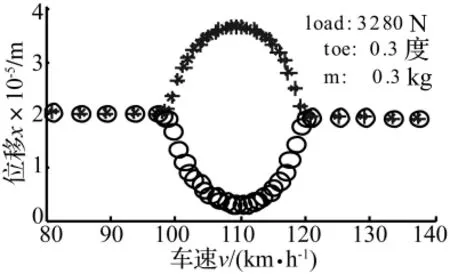
图6 正常工况下的胎面自激振动分岔图Fig.6 Bifurcation diagram of self-excited vibration of the tread under normal working condition

为研究系统的振动状态随着参数变化的规律，以便于更好地控制和避免轮胎多边形磨损现象，在图7中分别画出了改变车轮负载、接地块质量和前束角后的自激振动分岔图。其中，在同等载荷下接地块质量主要和轮胎的种类和花纹类型有关（如宽胎和窄胎）。从图中可以看出当载荷增加，接地块质量变小（轮胎越窄），前束角变大时，自激振动分岔范围均变大。

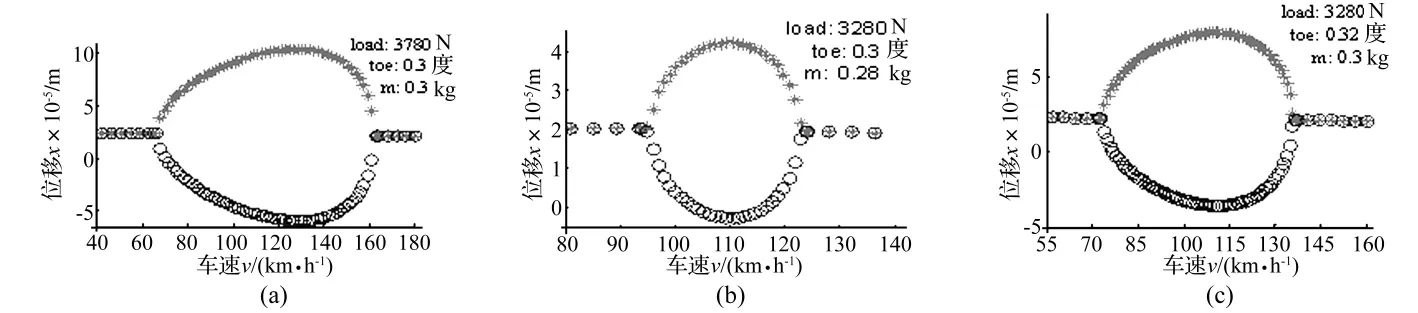
图7 不同工况下的胎面自激振动分岔图Fig.7 Bifurcation diagram of self－ excited vibration of the tread under differentl working condition

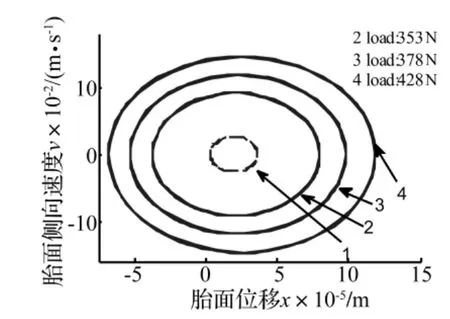
图8 不同载荷下的胎面自激振动相图Fig.8 Phase diagram of self-excited vibration of the tread under different loads

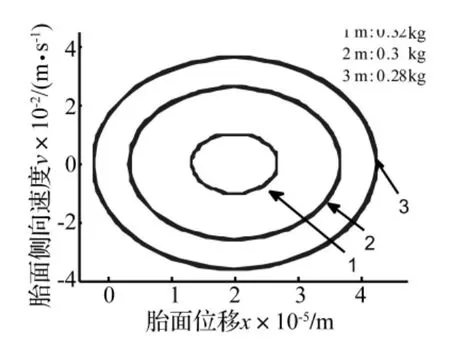
图9 不同接地印迹下的胎面自激振动相图Fig.9 Phase diagram of self-excited vibration of the tread under different ground bolt

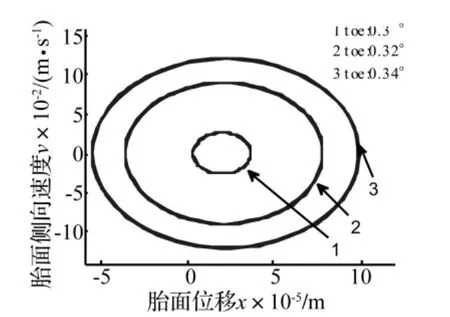
图10 不同前束角下的胎面自激振动相图Fig.11 Phase diagram of self-excited vibration of the tread under different toes

胎面的振幅大小和振动速度快慢反应了其振荡能量的大小，对轮胎磨损有着直接的影响关系，自激振动能量越强，多边形磨损越厉害。为更加清晰地阐述胎面振幅和振动速度变化与参数之间的关系，在图8～图10中给出了各参数下的相图。从图中得知，在同一车速下，载荷越大、接地块质量变小（轮胎越窄），前束角越大，胎面质量块的自激振动能量越大，对轮胎磨损的贡献量越大。这和轮胎在高速超载、前束角定位不当时更易出现多边形磨损现象的特征相吻合。

虽然通过降低车速可以避免自激振动的产生，但作为车辆性能的重要评价指标之一，长期保持低速行驶是不现实的。由此可见，为了更好地消除由胎面自激振动而引起的轮胎多边形磨损现象，应该避免汽车超载行驶，并调配好适当的前束角，或者更换宽胎使得能够产生自激振动的车速控制在合理范围之内。

5 结论

（1）本文主要研究了易产生多边形磨损的轮胎自激振动的形成机理，结合与试验模型一致的具有迟滞现象的摩擦系数曲线，用matlab/simulink软件建立了轮胎自激振动系统的仿真模型。

（2）通过改变模型中的仿真参数，模拟了不同载荷，不同轮胎（宽胎和窄胎）以及不同前束角下的各种工况对轮胎自激振动的影响，计算出了产生自激振动的分岔速度，并利用Lyapunov稳定性理论对其极限环稳定性进行了分析。

（3）得出载荷越大，轮胎越窄，前束角越大越容易出现轮胎多边形磨损的结论，为轮胎多边形磨损的研究提供了理论支撑。

（4）通过控制容易引起自激振动的敏感参数可以避免或者缩小使得轮胎产生自激振动的车速范围，最大程度上降低轮胎多边形磨损对汽车行驶的影响，具有较重要的工程意义。

［1］彭旭东，谢友柏，郭孔辉.轮胎摩擦学的研究与发展［J］.中国机械工程，1999，2（2）：215－219.

［2］黄海波，靳晓雄，丁玉兰.轮胎偏磨损机理及数值解析方法研究［J］.同济大学学报（自然科学版），2006，34（2）：234－238.

［3］ Heinrich G，Klüppel M.Rubber friction，tread deformation and tire traction［J］.Wear，2008.265：1052 －1060.

［4］ Walters M H.Uneven wear of vehicle tires［J］.Tire science and techno-logy，1993，21（4）：202 －219.

［5］ Sueoka A，Ryu T.Polygonal wear of automobile tire［J］.JSME，1997，40（2）：209 －217.

［6］李 勇，左曙光，雷 镭，等.基于LuGre摩擦模型的轮胎多边形磨损机理分析［J］.振动与冲击，2010，29（9）：108－112.

［7］杨宪武，左曙光，雷 镭，等.基于胎面－路面摩擦自激的轮胎非线性振动建模仿真［J］.振动与冲击，2010，29（5）：211－214.

［8］ Guo K H，Ren L，Hou Y P.A non-steady tire model for vehicle dynamic simulation and control［J］.AVEC’98，Nagoya Japan，1998.

［9］郭孔辉，庄 晔，Chen S K，等.汽车轮胎橡胶摩擦试验研究［J］.机械工程学报，2004，40（10）：179－184.

［10］彭旭东，郭孔辉，丁玉华，等.橡胶和轮胎的摩擦［J］.橡胶摩擦，2003，50（9）：562－568.

［11］ Mcmillan A J.A non-linear friction model for self-excited vibrations［J］. Journal of Sound and Vibration，1997，205（3）：323－335.

［12］ Canudas de Wit C，Olsson H，Astion K J，et al.A new model for control of systems with friction［J］. IEEE Transactionson Automatic Control， 1995， 40（3）：419－425.

［13］丁文镜.自激振动［M］.北京：清华大学出版社，2009.

［14］李 云.非线性动力系统的现代数学方法及其应用［M］.北京：人民交通出版社，1998.

［15］陆启韶.分岔与奇异性［M］.上海：上海科技教育出版社，1995.

［16］张继业，杨翊仁，曾 京.Hopf分岔的代数判据及其在车辆动力学中的应用［J］.力学学报，2000，32（5）：598－605.

［17］舒仲周，张继业，曹登庆.运动稳定性［M］.北京：中国铁道出版社，2001.