基于Teager能量算子的滚动轴承故障诊断研究

王天金，冯志鹏，郝如江，褚福磊

（1.北京科技大学 机械工程学院，北京 100083；2.石家庄铁道大学 机械工程学院，石家庄 050043；3.清华大学 精密仪器与机械学系，北京 100084）

滚动轴承失效常由轴承元件表面的局部损伤造成，如内圈、外圈、滚动体表面的点蚀、裂纹和剥落等。在轴承运动元件旋转效应的作用下，局部损伤点与其它元件反复接触，从而产生周期性冲击信号。理论上，周期性冲击以及相邻冲击之间的时间间隔是判断局部损伤故障的关键特征。如何从振动信号中有效提取冲击特征并识别冲击的重复频率，是滚动轴承故障诊断中的关键问题［1－3］。

近年来非线性信号处理领域中的Teager能量算子为提取滚动轴承故障信号中的瞬态冲击特征提供了一种有效途径。Teager能量算子是一种非线性差分算子，通过信号的瞬时值及其微分的非线性组合估计信号源产生动态信号所需的总能量（机械能，既包含动能又包含势能），能够增强信号的瞬态特征，适合检测信号中的冲击成分。该方法的时间分辨率高，对信号的瞬时变化具有良好自适应能力，而且计算复杂性低，算法效率高。

近年来，人们对Teager能量算子及其应用进行了探索性研究。Kaiser和 Maragos等［4－5］提出并完善了Teager能量算子，应用该方法对语音信号处理进行了深入研究。刘红星等［6］应用仿真信号和压缩机振动信号对比分析了Teager能量算子解调和Hilbert变换包络解调的性能，验证了该方法的有效性。Cheng等［7］将Teager能量算子解调方法与经验模式分解方法结合，分离本质模式函数中的瞬时幅值和瞬时频率，根据瞬时幅值变化的包络谱识别滚动轴承故障。Bassiuny和Li［8］应用经验模式分解分离机床进给电机电流信号中的调幅调频过程，然后应用Teager能量算子解调方法计算本质模式函数的瞬时幅值和瞬时频率，构造时频分布监测机床刀具状况。

本文针对滚动轴承故障诊断中的周期性冲击特征提取问题，利用Teager能量算子在检测信号瞬态成分方面的优势，增强突出滚动轴承故障振动信号中的冲击特征，由信号的瞬时Teager能量的Fourier频谱识别特征频率，从而判断故障原因。

1 Teager能量算子

对于任意信号x（t），Teager能量算子 Ψ定义为［4－5］：

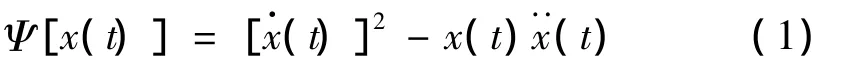
其中（t）和（t）分别为信号x（t）相对于时间t的一阶和二阶微分。实际上，Teager能量算子的输出追踪产生信号所需的总能量。

对于一个由质量为m的质量块和刚度为k的弹簧组成的线性无阻尼振动系统，根据Newton运动定律得二阶运动微分方程：

其中x（t）为质量块m相对于平衡位置的位移，（t）为x（t）相对于时间t的二阶微分，即加速度。该方程描述质量块的运动，它的解为简谐振动：

相应地，其一阶和二阶微分，即速度和加速度分别为：

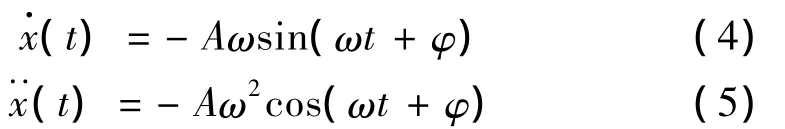
其中：A为振动幅值，（k/m）1/2为固有（圆）频率，φ为初始相位。

在任意时刻，该振动系统的机械能为弹簧中的势能和质量块的动能之和，即：

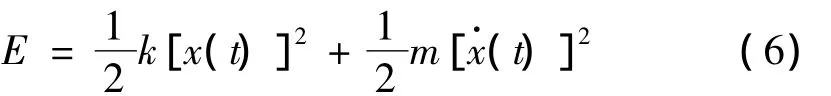
将式（3）和式（4）代入式（6），得：

式（7）表明简谐振动的瞬时总能量与振动的幅值和频率的平方成正比。

将式（1）定义的Teager能量算子Ψ作用于式（3）描述的简谐振动x（t），并分别应用式（4）和式（5）代替其一阶和二阶微分（t）和（t），得：

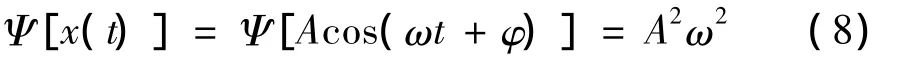
对比式（7）和式（8），可见Teager能量算子的输出和简谐振动的瞬时总能量之间只相差一个常数m/2，因此它跟踪产生简谐振动所需的总能量（在1/2倍的单位质量的意义上）。

式（1）中的Teager能量算子针对连续时间信号定义，对于离散时间信号x（n），应用差分代替微分，则Teager能量算子变为：

对于离散时间信号，Teager能量算子只需要三个样本数据计算任意时刻n处的信号源能量，因此，它对于信号的瞬时变化具有良好的时间分辨率，能够检测信号中的瞬态成分。

2 方法原理

若滚动轴承的内外圈或滚动体存在擦伤、裂纹、点蚀或脱落等局部损伤，则在滚动轴承运行过程中，当损伤点通过其它元件时，将导致接触表面之间的润滑油膜破裂，接触刚度和阻尼发生瞬间变化，导致振动能量突变，产生冲击现象。这种冲击会激发出轴承元件的共振，在结构阻尼的作用下，共振迅速衰减。因此，故障引起的瞬态冲击振动不仅幅值发生急剧变化，而且振动频率较高。

传统意义上的信号能量定义为信号幅值的平方，只代表动能或势能。它虽然也能够突出冲击的瞬态特征，但是，若冲击幅值较小，则冲击成分有可能被其它成分淹没。Teager能量算子跟踪产生信号所需的总能量，既包括动能又包括势能，其输出为振动瞬时幅值和瞬时频率二者的平方之积。相对于传统的信号能量定义，它增加了和频率平方的乘积。由于瞬态冲击的振动频率较高，因此它更能够突出冲击的瞬态特征。

故障轴承工作时，会产生周期性冲击，周期性冲击的重复频率反映轴承的故障原因。根据这一原理，本文提出了基于Teager能量算子的滚动轴承故障诊断方法：首先，利用Teager能量算子在检测瞬态冲击方面的优势，计算信号的Teager能量算子输出；然后，为了分析瞬态冲击的周期性质，对瞬时Teager能量序列进行Fourier变换，得Teager能量谱；最后，根据Teager能量谱中的主导频率成分和轴承元件的故障特征频率识别故障原因。

以下首先通过故障轴承振动的仿真信号分析说明该方法的基本原理，然后通过轴承外圈、内圈故障实验信号分析验证该方法的有效性。

3 仿真信号分析

故障滚动轴承产生的冲击振动信号可以模拟为［9］：

其中，A为冲击振动的幅值，ζ为阻尼特征常数，ωr为系统共振（圆）频率，u（t）为单位阶跃函数。

重复周期为T的周期性冲击振动信号为：

把式（10）带入式（11）得：

其中，T为冲击的重复周期，即轴承故障特征频率的倒数，τi为滚动体的随机滑动对特征频率产生的影响因子，可以取为 0.01T～0.02T。

在仿真信号中，取Am=1，ζ=0.15，ωr=1 000 πrad/s，T=0.025 s，τi为 0.01T～ 0.02T之间的随机数，M=40，采样频率为2 000 Hz。为了模拟实际测试中背景噪声的干扰，在信号中加入了Gauss白噪声，使得信噪比为－3 dB。该仿真信号的时域波形、功率谱、瞬时Teager能量波形和Teager能量谱如图1（a）～图1（d）所示。

为了对比分析，对仿真信号还进行了包络谱分析，如图1（e）所示。由功率谱可见，信号的主要成分集中在［300，700］Hz的频带内，由仿真信号模型可知共振频率为500 Hz，因此，包络谱分析过程中的预处理带通滤波器中心频率选为500 Hz，带宽选为400 Hz。

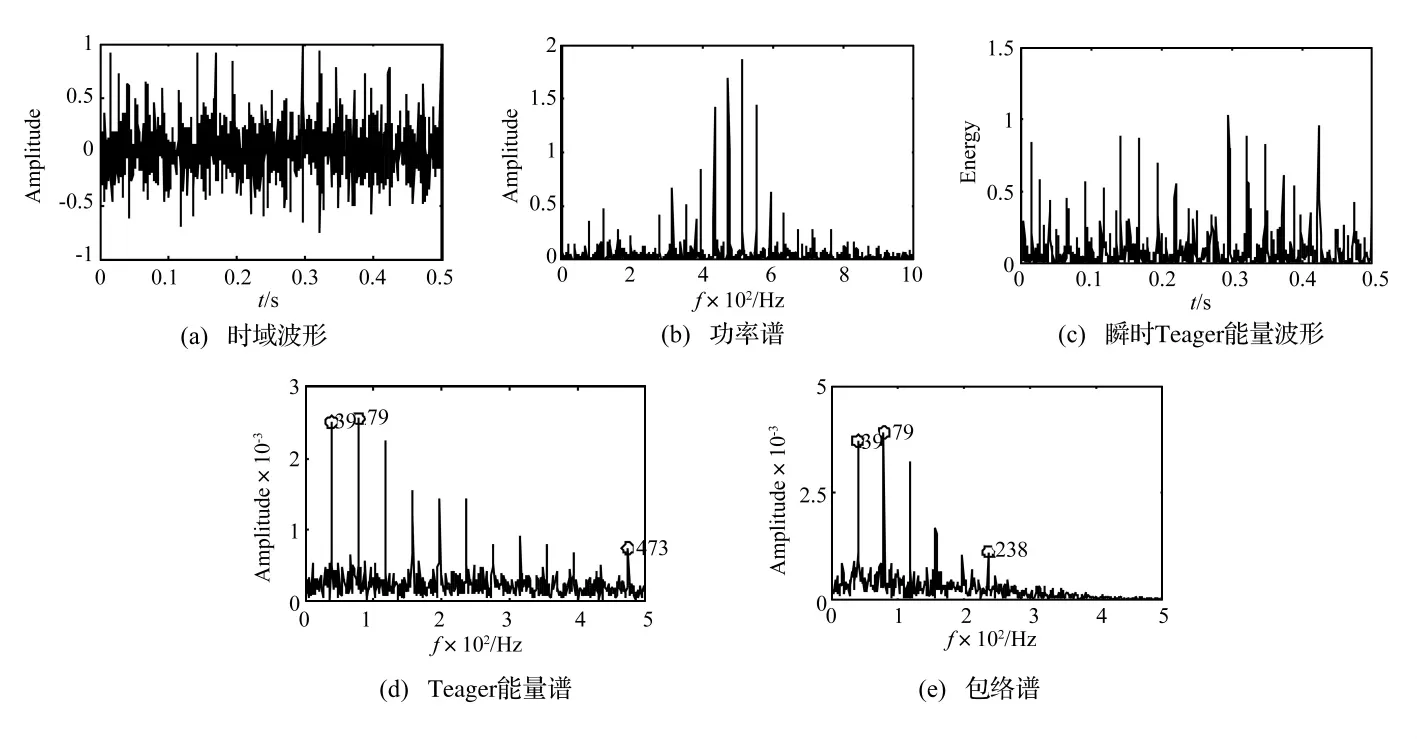
图1 仿真信号分析结果Fig.1 Analysis result of a simulated signal

由仿真参数可知，故障特征频率为40 Hz。在时域波形中，受噪声干扰的影响，周期性冲击特征不明显；而在瞬时Teager能量波形中，Teager能量算子突出了冲击特征，出现了周期性冲击成分，而且相邻两个冲击之间的时间间隔和故障特征频率对应，因此可以判断出现了故障；在功率谱中，峰值主要集中在共振频率500 Hz左右，需要根据边带频率之间的间隔来识别故障；在包络谱中，虽然峰值频率和故障特征频率及其倍频对应，能够说明出现了故障，但是提取出来的最高倍频成分仅为6阶；而在Teager能量谱中，可以清晰地识别故障特征频率及其倍频成分，且提取出来的倍频成分高达12阶，故障特征更加明显。可见，Teager能量谱能够增强故障特征，更加准确地提取滚动轴承的故障特征频率信息，表明该方法在滚动轴承故障诊断中具有很大潜力。

4 实验信号分析

4.1 实验说明

待测的滚动轴承型号为GB6220深沟球轴承，参数见表1。为了模拟滚动轴承各元件的局部损伤，分别在外圈、内圈用电火花加工一个直径为2 mm，深为1 mm的凹坑，如图2所示。

图3为实验的系统组成。试验滚动轴承支承转轴，交流电机通过V型带驱动转轴旋转。加速度传感器设置在待测轴承座的正上方。实验中，电机转速设定为444 r/min，作用在待测滚动轴承上的负载为15.68 kN，采样频率为10 kHz。根据滚动轴承的参数，分别计算各元件的故障特征频率，见表2。

表1 滚动轴承GB6220基本参数Tab.1 Parameters of rolling element bearing GB6220

图2 滚动轴承元件损伤Fig.2 Damage of rolling element bearing

表2 滚动轴承GB6220元件的特征频率（Hz）Tab.2 Characteristic frequency of rolling element bearing fault

图3 滚动轴承实验台Fig.3 Test rig of rolling element bearing

4.2 信号分析

滚动轴承的振动信号通常由安装在轴承座上的传感器来检测。滚动轴承外圈固定，与轴承座直接配合，它和传感器之间的位置相对固定，外圈故障产生的冲击特征在振动测试信号中比较明显。因此，轴承外圈故障比较容易诊断。而滚动轴承内圈直接和转轴相连，随着转轴旋转，传感器和内圈故障点之间的相对位置随之变化。只有在内圈故障点通过轴承负荷区时，才会在振动信号中出现明显的冲击特征。另外，内圈故障引起的冲击经过滚动体、保持架、外圈和轴承座以及中间界面的传递之后，能量衰减损耗较大。因此，内圈故障振动信号中的冲击特征不明显，内圈故障诊断相对较难。

为了验证Teager能量谱在滚动轴承故障诊断中的效果，以下首先分析正常轴承的振动信号，将结果作为基准，然后分析外圈故障信号，说明该方法的有效性，最后分析内圈故障信号，说明该方法在提取微弱故障征兆方面的性能。作为对比，还对上述信号进行了包络谱分析。由于信号的主导频率成分集中在［200，1 000］Hz的频带内，因此，包络谱分析过程中的预处理带通滤波器通带范围选为［200，1 000］Hz。

正常轴承振动信号的时域波形、功率谱、瞬时Teager能量波形、Teager能量谱和包络谱如图4（a）～图4（e）所示。可见，时域波形和瞬时Teager能量波形中没有周期性冲击特征，功率谱、Teager能量谱和包络谱中都没有与任何滚动轴承元件故障特征频率及其倍频相对应的峰值频率或频率间隔，表明轴承正常，没有故障。

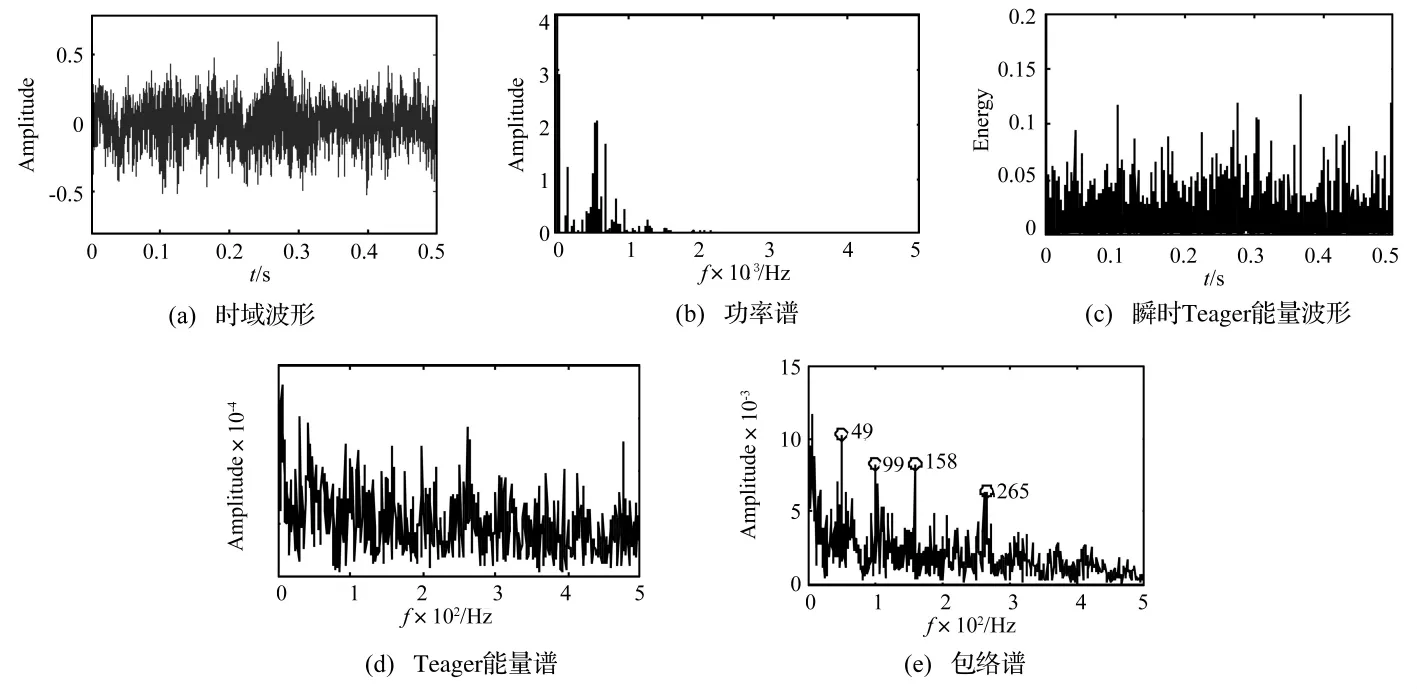
图4 正常滚动轴承信号分析结果Fig.4 Analysis result of normal bearing signal

外圈故障轴承振动信号的时域波形、功率谱、瞬时Teager能量波形、Teager能量谱和包络谱如图5（a）～图5（e）所示。可见，虽然时域波形中出现了冲击特征，但是并不明显；Teager能量算子突出了冲击特征，使得周期性冲击特征变得更加明显；功率谱中存在和轴承外圈故障特征频率对应的峰值频率和边带间隔，说明此轴承外圈存在故障；包络谱中的峰值频率和轴承外圈故障特征频率及其倍频相对应，但是峰值频率并不突出，而且提取出来的倍频成分阶次不连续；Teager能量谱中明显存在和轴承外圈故障特征频率30.3 Hz及其倍频相对应的峰值频率，而且倍频阶次连续，高达到16阶，故障特征更加明显直观。这表明Teager能量谱方法在诊断滚动轴承外圈故障时更加有效。

图5 滚动轴承外圈故障信号分析结果Fig.5 Analysis result of outer race damaged bearing signal

图6 滚动轴承内圈故障信号分析结果Fig.6 Analysis result of inner race damaged bearing signal

内圈故障轴承振动信号的时域波形、功率谱、瞬时Teager能量波形、Teager能量谱和包络谱如图6（a）～图6（e）所示。可见：时域波形中没有周期性冲击特征；功率谱中没有和内圈故障特征频率43.7 Hz相对应的峰值频率或边带间隔，因而无法识别故障原因；包络谱仅存在一个88 Hz的峰值和内圈故障特征频率的2倍频相对应，但峰值不突出，明显低于动力电源50 Hz的主导峰值，容易引起错误判断；瞬时Teager能量波形中存在周期性冲击，但是特征并不是非常明显；为了识别瞬时Teager能量波形中的周期性成分，对其进行Fourier变换，得到Teager能量谱，其中的峰值频率和内圈故障特征频率及其倍频相对应，提取出来的倍频阶次达到4阶，由此可以确定该轴承内圈出现了故障。

上述根据Teager能量谱方法得到的分析结果和实验中的真实情况完全吻合，本文提出的Teager能量谱方法不仅能够识别出故障特征明显的外圈特征频率，而且能够检测出故障特征微弱的内圈故障征兆，性能优于传统的包络谱方法。

5 结论

Teager能量算子计算产生信号所需的瞬时总能量，适合检测信号的瞬态变化，能够突出冲击信号的瞬态峰值特征。针对局部损伤滚动轴承振动信号的周期性冲击特点，提出了基于Teager能量算子的故障诊断方法：首先应用Teager能量算子计算信号的瞬时总能量；然后对瞬时Teager能量进行Fourier变换；最后根据Teager能量谱峰值和轴承故障特征频率判断故障原因。滚动轴承故障仿真信号和实验测试信号的分析验证了该方法的有效性，不仅准确识别了故障特征明显的外圈损伤，而且成功提取了故障特征微弱的内圈损伤特征。

［1］McFadden P D，Smith J D.Model for the vibration produced by a single point defect in a rolling element bearing［J］.Journal of Sound and Vibration，1984，96（1）：69－82.

［2］Tandon N，Choudhury A.A review of vibration and acoustic measurement methods for thedetection of defects in rolling element bearing ［J］.Tribology International，1999，32：469－480.

［3］冯志鹏，刘 立，张文明，等.基于小波时频框架分解方法的滚动轴承故障诊断［J］.振动与冲击，2008，27（2）：110－114.

［4］ Kaiser J F.On a simple algorithm to calculate the‘energy’of a signal［C］.Proceedings of IEEE International Conference on Acoustics， Speech， and SignalProcessing， 1990， 1：381－384.

［5］ Potamianos A，Maragos P. A comparison of the energy operator and Hilbert transformapproaches for signal and speech demodulation ［J］. SignalProcessing，1994，37（1）：95－120.

［6］刘红星，陈 涛，屈梁生，等.能量算子解调方法及其在机械信号解调中的应用［J］.机械工程学报，1998，34（5）：85－90.

［7］ Cheng J，Yu D，Yang Y.The application of energy operator demodulation approach based on EMD in machinery fault diagnosis［J］.Mechanical Systems and Signal Processing，2007，21（2）：668－677.

［8］ Bassiuny A M，Li X.Flute breakage detection during end milling using Hilbert-Huang transform and smoothed nonlinear energy operator［J］.International Journal of Machine Tools and Manufacture，2007，47（6）：1011－1020.

［9］ Ho D，Randall R B.Optimisation of bearing diagnostic techniques using simulated and actual bearing fault signals［J］.Mechanical Systems and Signal Processing，2000，14（5）：763－788.