电磁轨道发射状态下导轨的动态响应

田振国，白象忠，杨 阳

（燕山大学 建筑工程与力学学院，河北 秦皇岛 066004）

电磁轨道发射装置在军事和工业领域中有巨大的应用潜力，但是，一些难以克服的问题却阻碍了它从实验室走向实际应用的进程［1］。例如，为达到高速重复发射的要求，该如何克服导轨发射过程中导轨内侧烧蚀的问题?从而达到高速重复发射的要求；如何实现小体积大能量的发射要求?等等。目前国内外学者一方面着眼于改善导轨或导轨内侧的材料，或者通过采用新的导轨与电枢间的导电方式来避免导轨烧蚀；另一方面，通过计算导轨发射过程中导轨的动态响应及导轨的应力应变状态，来分析导轨发射状态下的受力及变形规律［2］。文献［3］将导轨简化为弹性地基梁，并假设电枢匀速通过导轨的情况下，讨论了导轨长度等参量对共振速度的影响。文献［4］研究了发射状态下导轨的弹性波，并讨论了电枢临界速度与接触压力之间的关系。文献［5］通过数值模拟的方法，研究了等离子体的粘滞阻力和惰性阻力对电枢运动的影响。但是，这些研究都没有考虑电枢对导轨作用力和电枢的变加速运动的特征。到目前为止，对电枢加速运动状态的导轨响应的研究，仍然十分少见。

电磁轨道发射器在发射过程中，当电流通入导轨后，电枢受到强大的推力作用，将沿导轨作变加速运动。由导轨间电磁场分布及通入电枢的电流强度值，可以得到电枢在发射过程中所受到的推力，进而得到电枢的运动方程；再通过计算导轨间相互作用的斥力与在焦耳热作用下电枢的膨胀量，则可得到导轨上的移动荷载值及其变化规律。考虑导轨发射装置的实际结构，将简化为弹性地基梁的导轨控制方程进行Fourier变换，便可导出发射过程中导轨的动态响应方程及其解。通过算例，分析了导轨几何参数、通入电流的强度及外包层的弹性特征等量对导轨动态响应的影响，从而可为发射轨道的设计提供理论计算的依据。

1 导轨的动力学控制方程及其求解

电磁导轨发射装置结构如图1所示。电流由一侧导轨流入，流经电枢，然后由另一侧导轨返回；电枢在两导轨间产生的强磁场受到电场力与洛仑兹力作用后，沿导轨滑动。在此过程中，导轨受到导轨间相互作用的斥力、电枢作用在导轨上的压力和导轨周围固定装置的弹性支撑反力的作用，因此，可将导轨看作如图2所示的弹性地基梁，其动力学控制方程为［6］：

式中：w（x，t）为导轨挠度，q（x，t）=q1（t）［1－H（xl（t））］+q2（t）H［a2－（x－l（t））2］为作用在导轨上的移动荷载，EI为导轨的抗弯刚度，k为地基弹性系数，ρ为导轨材料的质量密度，h、d分别为导轨的厚度和高度。q1（t）为导轨间相互作用的斥力集度，q2（t）为电枢作用在导轨上压力的集度，2a为电枢沿导轨方向的长度，l（t）为t时刻电枢沿导轨移动的距离，H（xl（t））、H［a2－（x－l（t））2］均为 Heaviside阶跃函数。

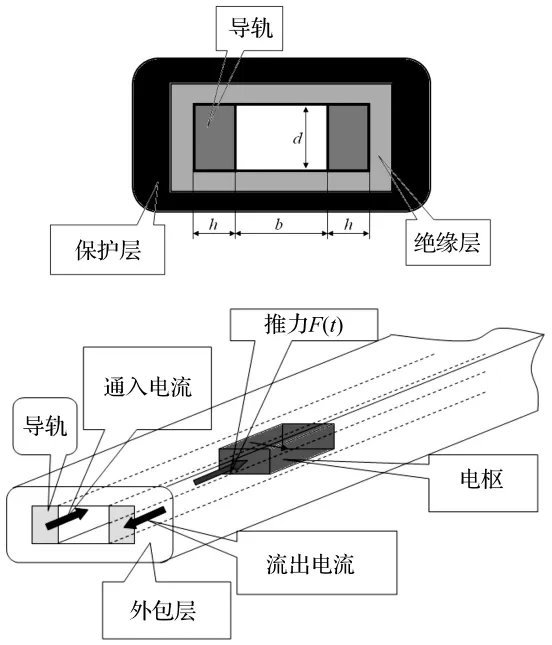
图1 导轨发射装置简图Fig.1 Schematic of rail launcher

将式（1）进行关于x、t的二维 Fourier变换，得［7］：

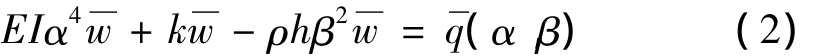
其中，α，β为二维Fourier变换中的积分变量。则：

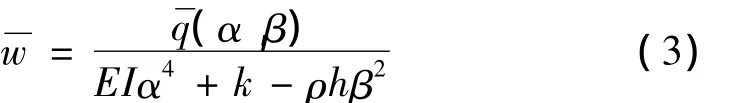
将式（3）进行 Fourier逆变换即可得到导轨挠度，即：

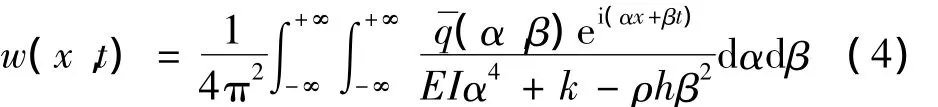
式（4）即为导轨发射过程中导轨挠度w（x，t）的表达式。

图2 导轨发射状态的受力简图Fig.2 Schematic of loading at launching state

2 发射过程中导轨及电枢的受力分析

2.1 导轨发射过程的机电模型

将导轨发射器看成是电源的一个负载，导轨为沿其长度分布的电阻和电感。在正常发射状态下，发射器后堂电压为［8］：

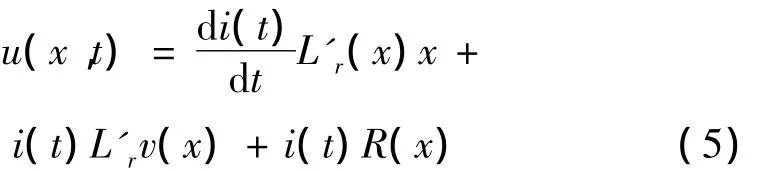
其中：L'r为导轨电感梯度，i（t）为流经导轨的电流强度，v（x）为电枢速度，R（x）为系统电阻。

考虑到导轨的趋肤效应及系统电感，在平顶脉冲电流激励下，导轨发射装置的负载电阻和电感分别为：

根据系统能量，可计算出电枢沿导轨移动距离为［8］：

采用迭代法，把放电电压作为初始量，由式（6）～式（8）可计算出系统电流强度、电感、电阻、电枢移动距离以及趋肤深度等量，根据这些参量得到新的后堂电压。如此反复，就可以计算出发射过程中实时的电流强度、系统电阻、电感、电枢的移动距离。

2.2 电枢推力的计算

如图3所示，根据通入导轨的电流强度i（t）可以得到导轨间任一点A（xA，yA，zA）的磁感应强度，再考虑到电枢的电流密度，则可计算出电枢上任一点受到的洛仑兹力［9］。由此，对其沿整个电枢体积进行积分，便可得到电枢受到电磁驱动力沿轨道方向的合力。随着电枢的移动，整个电流通路的电阻也将发生变化。如果外加的是稳恒电源，那么通入轨道的电流强度、导轨间的磁场、流经电枢的电流密度、电枢受到的推力都将是时间的变量。在图3所建立的坐标系中，电枢受到的推力经推导为：

其中：b为两导轨间距离，μ0为真空磁导率。

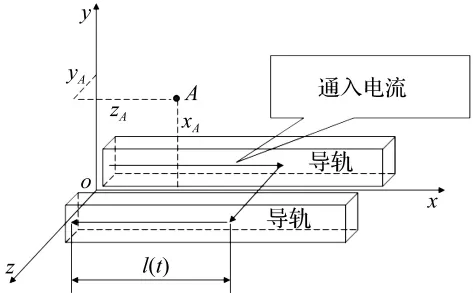
图3 坐标系的建立Fig.3 Establishment of coordinate

2.3 两导轨间相互作用斥力的计算

导轨通入电流后，导轨间产生磁感应强度为B的电磁场，由安培力计算公式 dF=i（t）dl×B［9］，经推导可得电枢经过的导轨部分导轨间的斥力的集度为：

2.4 电枢与轨道间接触力计算

当电流流经电枢时，由于焦耳热效应，电枢内势必产生热量。因电磁轨道发射装置通常采用电容单次放电的形式，可近似地认为电流在电枢内均匀分布。如果仅仅考虑电枢表面与外部的热交换——即电枢所发出的热量：一部分用于增加电枢的焓，另一部分则损失于外界——电枢温度就会沿电枢y方向分布为［10］：

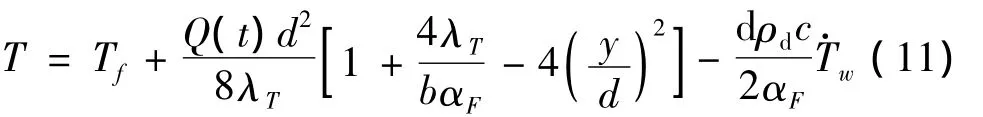
假设两侧轨道限制了电枢的热膨胀，且沿y方向取平均温度作为电枢应变的计算依据，由于作用时间非常短暂，可忽略温度随时间的变化，则得电枢的热应变为［11］：

式中αT为电枢材料的线膨胀系数。电枢作用在轨道上荷载的集度为：

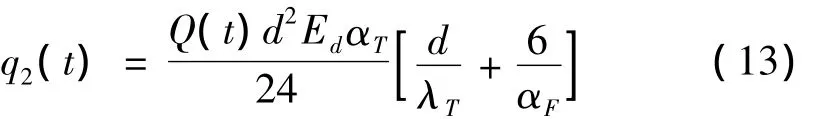
其中Ed为电枢材料的弹性模量。

3 发射过程中导轨的动态响应

当导轨通入强电流后，电枢将沿导轨变加速向前滑动，电枢滑动过的导轨部分受到相互作用的斥力和电枢对导轨的作用力。考虑式（1）、和式（2）经Fourier变换有：

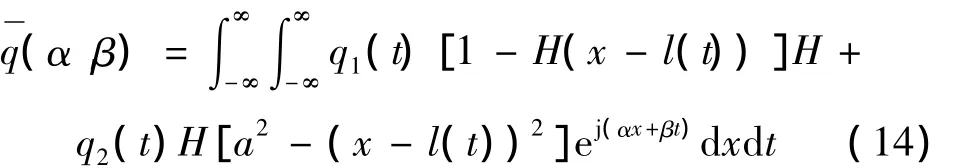
可得电枢沿轨道滑动时导轨挠度表达式为：

再考虑到式（10）、式（13）则可得导轨发射过程中导轨的动态响应，应用Matlab软件编制程序即可得到导轨挠度的数值解。

4 算例分析

如图1所示，取导轨的长度为2 m，高度d=20 mm，厚度h=20 mm，两导轨间距离b=20 mm；铜质导轨的质量密度为ρ=8 900 kg/m3，弹性模量E=100 GPa，泊松比 ν=0.3，电导率 σ =5.88 ×107（Ω·m）－1；导轨电感梯度L'r=0.451 24 μH/m。系统初始电阻R0=0.001 5 Ω，初始负载电感L0=0。铝质电枢沿导轨方向长度2a=20 mm，厚度为20 mm，高度为20 mm，电导率为 σD=3.6 ×107（Ω·m）－1，质量密度为 ρd=2 700 kg/m3，线膨胀系数 αT=2.35 ×10－5（℃）－1，热传导系数 λT=237 W/（m·℃），弹性模量Ed=100 GPa，表面放热系数αF=500 W/（m2·℃）。系统放电电压U0=800 V，真空磁导率 μ0=1.256 ×10－6H/m，地基弹性系数k=10 GPa，导轨两端自由。

图4 导轨挠度随时间变化规律Fig.4 Variation of rail’s deflection with time

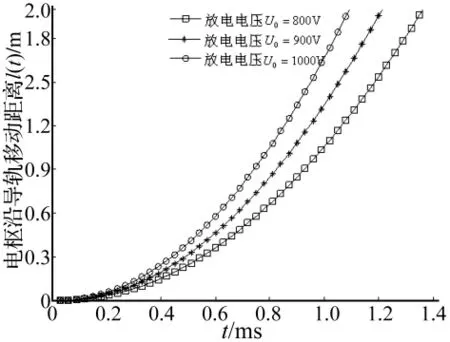
图5 电枢移动距离随时间变化曲线Fig.5 Curves of armature moving distance with time

图4为电磁轨道发射过程中导轨挠度的变化规律。从图中可以看出导轨不同位置的挠度随着电枢移动的动态响应。图5为在不同放电电压情况下，电枢在导轨中的移动情况，可见通入电压越高，发射时间越短。当放电电压U0=1 000 V时，电枢移动至发射端口只需 1.06 ms。

图6为在不同放电电压情况下电枢沿导轨滑动速度的变化曲线。图中可见，当放电电压为U0=800 V时，出口弹丸出口速度大约为3 013 m/s。图7为距发射端1.2 m处导轨挠度随电枢滑动位置的变化曲线。从图7中可以看出仅考虑导轨间斥力作用时，导轨发射前段此位置的挠度很小；当电枢到达1.2 m处时，此处挠度急剧增大，电枢经过后挠度缓慢变小。当仅考虑电枢对导轨作用时，导轨发射前段此位置挠度很小；当电枢到达1.2 m处时，此处挠度急剧增大，且影响程度比导轨间的斥力大得多；可当电枢经过此处后，此处的挠度迅速减小，这也正反映了两种载荷的不同性质。图8反映了导轨不同位置的挠度随电枢移动距离的变化而变化。不难看出：图中不同位置的挠度出现峰值的时间不同。当电枢滑动至相应位置时，挠度出现峰值，且不同位置的峰值是不同的。这是由于电枢移动过程中，系统电阻和电感变化导致电流密度发生变化造成的。

图6 电枢速度随电枢移动距离变化曲线Fig.6 The velocity curves of armature versus the armature moving distance

图7 导轨1.2 m处挠度随电枢移动距离变化曲线Fig.7 Variation of deflection at 1.2m of rail versus the armature moving distance

图8 导轨不同位置挠度随电枢移动距离变化曲线Fig.8 Deflection of different place versus the armature moving distance

图9 放电电压对导轨1.2 m挠度的影响Fig.9 The effect of discharge voltage on deflection of rail 1.2 m

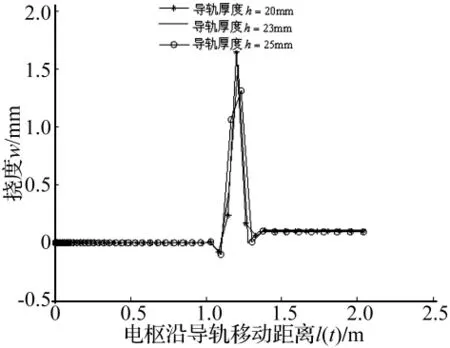
图10 导轨厚度对挠度的影响Fig.10 The effect of rail thickness on deflection of rail

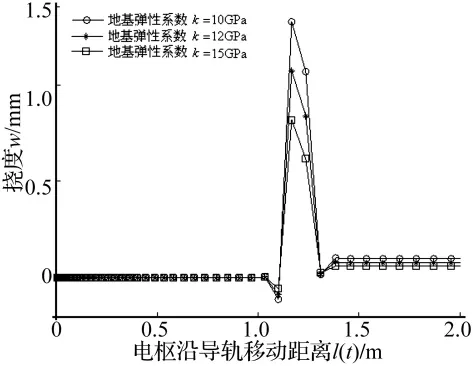
图11 地基弹性系数对导轨挠度的影响Fig.11 The effect of elasticity coefficient on deflection of rail

图9、图10、图11分别讨论了距发射端1.2 m处导轨挠度与放电电压、导轨厚度以及地基弹性系数的关系。可见，此处导轨挠度的峰值总是在电枢经过该处时出现。地基弹性系数越小，放电电压越大，其挠度峰值也越大。这是由于电压增大，电枢膨胀量变大，施加在导轨上的载荷增大，导轨约束变弱而导致的。导轨厚度变化影响电流密度值、导轨间磁场以及导轨的抗弯刚度。然而，就综合影响来看，导轨刚度的增加是导致其挠度变小的主要原因。

5 结论

由计算结果可见：

（1）导轨的动态响应与通入电流的强度、导轨的尺寸、外包层的刚度等参数有关。导轨间作用与电枢对导轨的作用相比，显然电枢对导轨动态响应的影响起主要作用。

（2）导轨挠度的最大值具有随着电枢移动而移动的特征。

（3）增大外包层刚度，或者降低放电电压，均可以有效地减小导轨的变形。

从实际需要考虑，欲达到出口高速度就必须增大电压，减少系统电阻，改善电枢材料的力学及传热学性能。例如选择导电性能良好而热涨系数和质量很小的材料作电枢，将是提高出口速度、降低导轨变形的有效方法。最佳参数的选择，都可以通过理论分析和数值计算得到。

［1］李立毅，李小鹏.电磁发射的历史及发展趋势［J］.微电机，2004，37（1）：41－44.

［2］范长增，王文魁.发展中的电磁轨道炮［J］.燕山大学学报，2007，31（5）：377 －386.

［3］Jerome T T，Wei S.Dynamic response of cantilevered rail guns attributed to projectile/gun interaction-theory［J］.IEEE Transactions on Magnetics，2007，43（1）：207－213.

［4］ Anthony J，Johnson F C，Moon.Elastic waves and solid armature contact pressure in electromagnetic launchers［J］.IEEE Transactions on Magnetics，2006，42（3）：422 －429.

［5］杨玉东，王建新.电磁炮发射原理数值建模与分析［J］.火炮发射与控制学报，2008（4）：9－13.

［6］谢伟平，王国波.移动荷载作用下轨道系统的动力特性分析［J］.郑州大学学报，2003，24（1）：24－27.

［7］华中理工大学数学系.复变函数与积分变换［M］.北京：高等教育出版社，2002：180－206.

［8］王 莹，肖 峰.电炮原理［M］.北京：国防工业出版社，1995：17－88.

［9］俎栋林.电动力学［M］.北京：清华大学出版社，2006：48－136.

［10］米海耶夫M A.传热学基础［M］.北京：高等教育出版社，1958：338－378.

［11］白象忠，田振国.板壳磁弹性力学基础［M］.北京：科学出版社，2006：51－84.