正交面齿轮传动非线性振动特性分析

林腾蛟，冉雄涛

（重庆大学 机械传动国家重点实验室，重庆 400030）

面齿轮传动是一种圆柱齿轮与面齿轮相啮合的传动形式，用于实现传递轴与被传递轴存在一定角度的运动。作为一种新型传动形式，面齿轮传动具有结构简单、重量轻、传动重合度大、振动噪声小等诸多优点，在直升机减速器等重要航空传动装置中具有广阔的应用前景。鉴于面齿轮传动的诸多优点，国内外学者自上世纪90年代以来相继开展了面齿轮的相关研究工作，包括齿面生成原理、啮合特性、强度分析、加工方法及装备、面齿轮传动试验等［1－8］。目前对于非线性振动特性研究，主要集中在圆柱齿轮、行星齿轮及螺旋锥齿轮传动等［9－12］，对面齿轮传动振动特性分析还较少见。2009年，靳广虎等［13］建立了正交面齿轮传动系统的弯－扭－摆耦合振动模型，分析了传动误差对系统动载系数的影响；陈广艳等［14］建立了含面齿轮的直升机主减速器传动系统动力学模型，对前飞和悬停飞行状态下面齿轮动态响应特性进行分析。但两篇文献均未考虑齿侧间隙、齿面摩擦、轴承间隙等强非线性因素对系统非线性振动特性的影响。

本文在已有研究的基础上，采用集中参数法，建立包含时变啮合刚度、啮合阻尼、齿面误差、齿面摩擦、齿侧间隙、轴承间隙等多种因素的正交面齿轮传动系统的弯－扭耦合非线性动力学模型，利用4～5阶变步长Runge-Kutta法求解系统的动力学微分方程组，得出系统的非线性振动特性以及各参数对系统动态特性的影响。

1 非线性动力学模型

1.1 动力学模型及参数

根据集中参数理论，建立如图1所示的正交面齿轮传动系统动力学模型，支承轴承采用弹簧模拟，模型中不考虑齿轮绕各坐标轴的摆振。面齿轮传动的主要参数如表1所示。

图1 正交面齿轮传动系统动力学模型Fig.1 Dynamic model of face-gear drive system

表1 面齿轮传动系统参数Tab.1 Parameters of face－gear drive system

1.2 时变啮合刚度及综合误差

由于面齿轮副啮合的重合度大于1，即在一个啮合周期内，齿轮副均存在双齿啮合和单齿啮合区。在单双齿啮合区的交界处，齿轮副的综合啮合刚度会发生阶跃性突变。因此，实际的面齿轮副的综合啮合刚度是一个以啮合周期为周期的周期函数，可将其处理为一个不变的平均值加上一个周期波动值，表达式为：

式中，Km为啮合刚度的平均值，Kr为啮合刚度的波动幅值，ωh为齿轮副的啮合频率，φr为初始相位角。

由于齿轮加工误差和安装误差的存在，必然会引起齿轮瞬时传动比发生变化，造成轮齿之间碰撞和冲击。对于静态传递综合误差，可以采用简谐函数对其进行模拟，一般将其表示为：

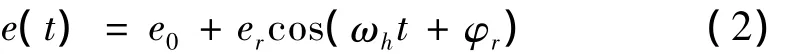
式中，e0和er分别为齿轮副法向静态传递综合误差的常值和变量幅值，φr为初始相位角。

1.3 动力学微分方程

在图1所示的模型中，以主动轮1和从动轮2的轴线交点为原点建立直角坐标系。两齿轮用集中质量和转动惯量模拟，且齿轮轴被视为刚性，轴两端的支承被等效处理为作用在两齿轮轴线方向的中心点沿x，z方向的刚度和阻尼。由于小齿轮为直齿圆柱齿轮，齿轮上无轴向作用力，因此可以只考虑两齿轮分别沿x，z的平移振动自由度及轮体绕各自轴线方向的转动自由度。故整个传动系统共有6个自由度，表示为：

齿轮副在啮合点处因振动位移和误差产生的沿啮合点法线方向的相对位移δn为：

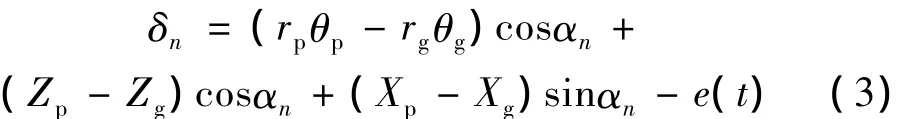
式中：rp为圆柱齿轮分度圆半径，rg为面齿轮的名义半径，rg=mz2/2［14］，θp，θg分别为圆柱齿轮和面齿轮扭转角位移，αn为圆柱齿轮和面齿轮的法面压力角。

齿轮副啮合时的法向动载荷及其沿各个坐标轴上的分量为：

式中，ch为啮合阻尼，f（δn）为具有分段线性特征的间隙非线性函数，其表达式为：

式中，bh为齿侧间隙之半。

设主动轮上的输入转矩为Tp，从动轮上的负载转矩为Tg。考虑到支承齿轮轴的轴承存在一定的间隙，同样用间隙非线性函数来表示。设轴承沿x、z方向的间隙为bIj（I=X，Z，j=p，g），则轴承各方向的支承力可表示为：

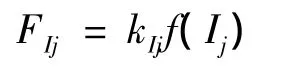
根据牛顿第二定律，得到图1所示的正交面齿轮传动系统的动力学微分方程为：

式中，mp、mg、Jp、Jg分别为两齿轮的质量和转动惯量，μ为滑动摩擦系数，lp为时变摩擦力矩，η为摩擦力方向函数。

已知齿轮副重合度ε，小齿轮转速为ω1、基圆半径rb1、齿顶圆半径ra1、基圆齿距Pb1，则摩擦力臂及摩擦力方向函数可表示为：

以齿面啮合点间的法向相对位移δn为新的自由度，对式（6）中的两轮扭转振动方程进行合并处理可得：

式中，me为齿轮副等效质量，me=JpJg/（r2pJg+r2gJp）；

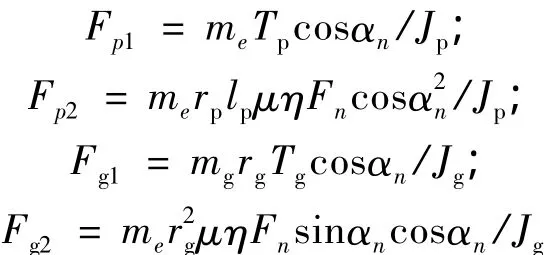
将上述振动方程进行量纲一化处理后，得到：

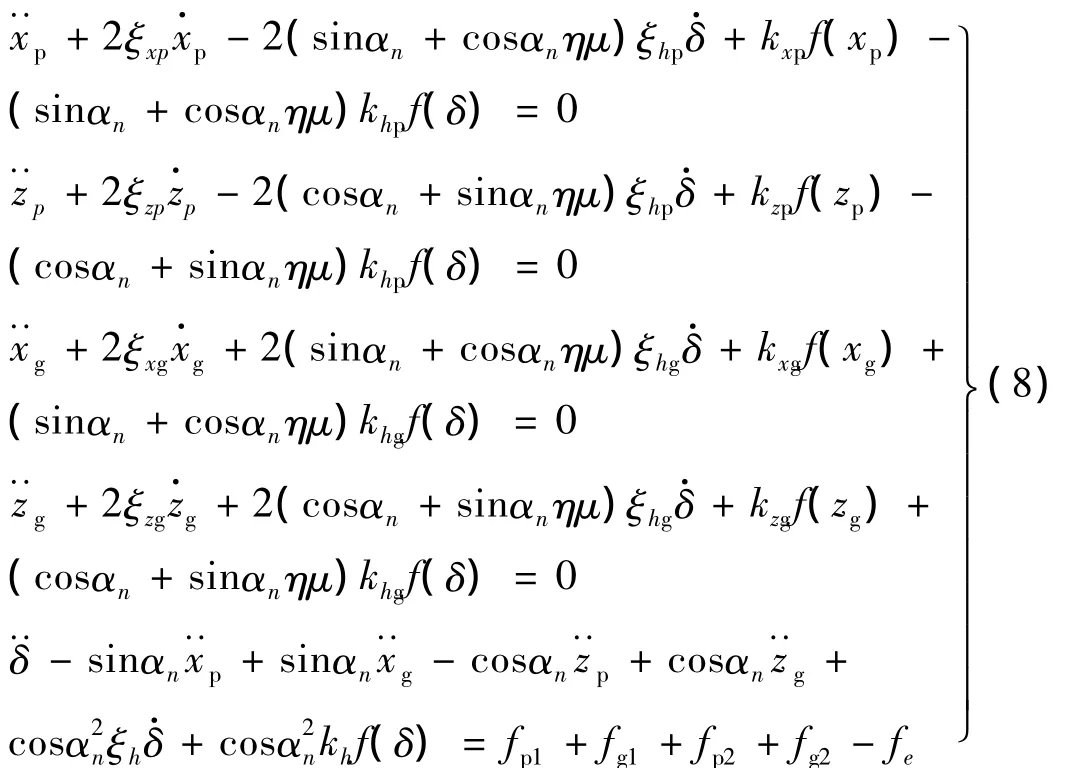
式中：

以上各式中，I=X，Z；i=x，z；j=p，g；d=1，2。

2 非线性动力学特性分析

方程（8）是一个强非线性变参数动力学微分方程组，本文采用4－5阶变步长自适应龙格库塔法对其进行求解，求解中积分步长取为Tm/300（Tm=2π/Ω，为量纲一化后的啮合周期），积分时间取为500Tm。舍弃前面的数百周期，取后面部分做系统响应的时间历程图、相图、Poincaré映射及FFT频谱图。

2.1 啮合频率对系统非线性动力学特性的影响

图2 位移－频率分岔图Fig.2 Displacement-frequency bifurcation diagram

取滑动摩擦系数μ=0.02，齿轮副无量纲啮合频率Ω在0～2范围内变化，得到系统的相对位移响应随啮合频率变化的分岔图，如图2所示。由图可知，系统响应呈现出复杂的运动状态，响应出现多次跳跃现象，而且在多数跳跃点处系统的运动状态也随之发生改变。总体看来，系统响应状态经历了拟周期－混沌－周期－混沌的运动状态，混沌区域与周期窗口交错出现，有些周期窗口比较狭窄，但有些则范围比较大，在实际运转中可以通过调节输入转速，使系统运动状态处在位移较小的周期窗口中，能够有效地降低系统的振动。

当无量纲频率Ω＜0.4时，系统一直处于拟周期响应，0.4＜Ω＜0.433时出现了一个比较狭窄的单周期窗口，如图3所示。从时间历程图可看出响应是周期为T（T=2π/Ω）的周期运动，相图为非圆闭合曲线，Poincaré截面上为单个离散点，FFT频谱图在iΩ（i为正整数）处有幅值分量，表明系统响应存在超谐成分。

图3 单周期非谐响应（Ω=0.42）Fig.3 Single period non-harmonic response

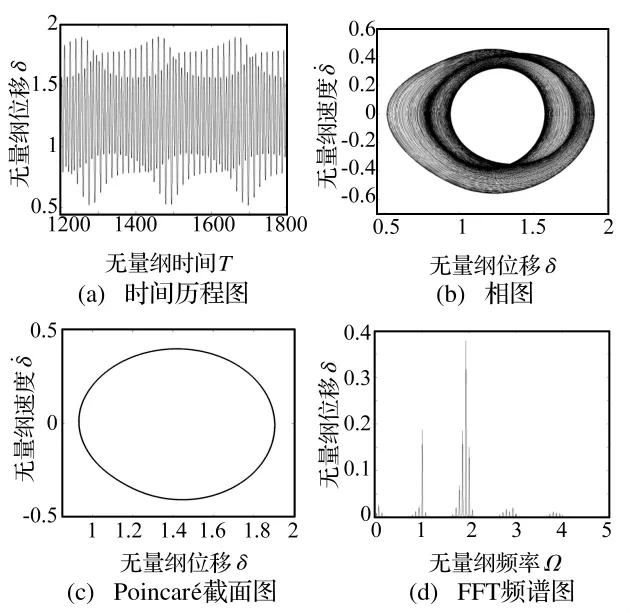
图4 拟周期响应（Ω=0.433）Fig.4 Quasi periodicity response

当Ω=0.433时系统又呈现拟周期响应，如图4所示。拟周期响应是由两个或以上的不可通约的频率成分组合而成的，从时间历程图上能够看出响应存在周期成分，相图为具有一定宽度的闭合曲线带，Poincaré截面为封闭曲线，FFT频谱图的谱线离散地分布在组合频率的点上。

当Ω=0.55时系统呈现2周期次谐波响应。Ω增大到0.586时系统进入混沌响应，如图5所示。从时间历程图上看不出任何周期特性，相图为充满空间某一部分且既不重复又不封闭的曲线，在Poincaré截面上，起始时相点虽然随机地分布着，但在计算足够长的时间以后，一种由相点描绘的内部结构逐步地显露出来，而FFT频谱图则表现为一定范围内的连续谱。

图5 混沌响应（Ω=0.586）Fig.5 Chaotic response

图6 8周期次谐波响应（Ω=1.4）Fig.6 Eight-period sub-harmonic response

当Ω在0.594～1.165的范围时，系统处于复杂的周期运动状态，并且存在跳跃现象，而且每个跳跃点都伴随着周期的改变。在Ω处于0.594～0.94时系统为单周期响应，当Ω继续增大时系统响应发生跳跃，变为3周期运动。随后倍周期分岔为6周期运动，之后又回到3周期运动，在Ω=1.09处又发生跳跃，变为单周期运动。

当Ω继续增大时，系统经倍周期分岔进入混沌。Ω=1.2时系统为单周期响应，Ω=1.22时系统为2周期响应，Ω=1.3时系统为4周期响应，Ω=1.4时系统为8周期响应，如图6所示，Ω=1.44时进入混沌运动，如图7所示。

图7 混沌响应（Ω=1.44）Fig.7 Chaotic response

2.2 负载转矩对系统非线性动力学特性的影响

定义载荷系数C=Tv/Tg，其中Tv为负载转矩，Tg=1 727.3 N·m为额定输出转矩。取滑动摩擦系数μ=0.02，C在0～2之间变化，追踪系统响应得到相对位移随载荷系数变化的分岔图，如图8所示。

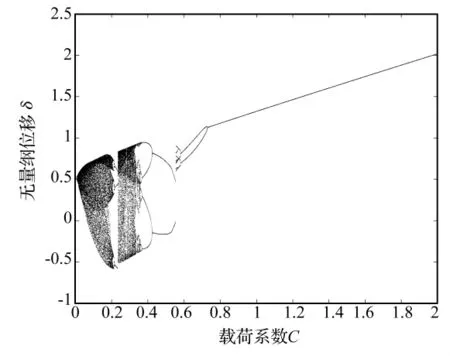
图8 位移－载荷系数分岔图Fig.8 Displacement-load factor bifurcation diagram

根据齿侧间隙非线性函数可知，当无量纲位移δmax＞1且δmin＜－1时，齿轮副处于双边冲击状态，当δmax＜1且 δmin＞ －1时，齿轮副处于无冲击状态，当δmax＞1或 δmin＜ －1时，齿轮副处于单边冲击状态。

当载荷系数C=0.15时系统为混沌响应，如图9所示。由时间历程图可知齿轮副处于双边冲击状态。

图9 混沌响应（C=0.15）Fig.9 Chaotic response

当载荷系数继续增大，在混沌区域出现一个狭窄的周期窗口。取C=0.23时，系统为3周期次谐响应，如图10所示。由时间历程曲线可以看出此时齿轮副处于单边冲击状态。

图10 3周期次谐波响应（C=0.23）Fig.10 Three-period sub-harmonic response

当载荷系数增大到C=0.3时，系统又进入混沌响应，如图11所示。由时间历程曲线可以看出此时系统响应幅值继续增大，齿轮副处于双边冲击状态。

在载荷系数C处于0.4～0.6之间变化时，系统响应均处于多周期运动状态，且伴有倍周期倒分岔及跳跃现象，且在跳跃点处系统的周期运动状态发生改变，如图12～图15所示。从各时间历程曲线上可看出系统均处于单边冲击状态。

当载荷系数增大到C=0.96时，系统处于单周期响应，如图16所示。无量纲位移幅值显著增大，δmin＞1，此时齿轮副始终保持接触而不脱啮，处于无冲击状态。

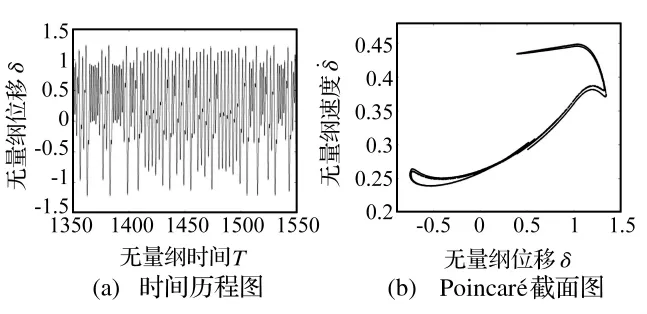
图11 混沌响应（C=0.3）Fig.11 Chaotic response

图12 4周期次谐波响应（C=0.4）Fig.12 Four-period sub-harmonic response

图13 2周期次谐波响应（C=0.5）Fig.13 Two-period sub-harmonic response

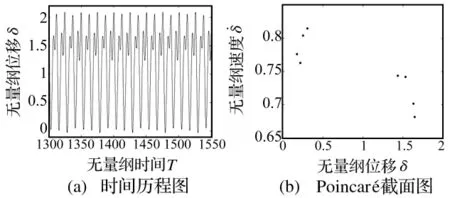
图14 8周期次谐波响应（C=0.56）Fig.14 Eight-period sub-harmonic response

图15 2周期次谐波响应（C=0.6）Fig.15 Two-period sub-harmonic response

图16 单周期非谐响应（C=0.96）Fig.16 Single period non-harmonic response

由以上分析可知，负载转矩的大小对系统响应影响甚大，在负载转矩逐渐由小增大的过程中，齿轮副的啮合状态也逐渐从双边冲击、单边冲击进入到无冲击状态。每次啮合状态的变化均伴随着系统响应特性的变化，或出现分岔，或出现跳跃。在负载转矩较小时，齿轮副未能始终处于啮合状态，容易产生冲击。当负载增大到一定数值时，齿轮副弹性接触变形较大，始终保持啮合状态，无冲击现象出现。

2.3 摩擦系数对系统非线性动力学特性的影响

取载荷系数为C=1，Ω=1.15，其它参数保持不变，μ在0～0.1范围内逐渐增大时，得到如图17所示的系统的相对位移响应随摩擦系数变化的分岔图。

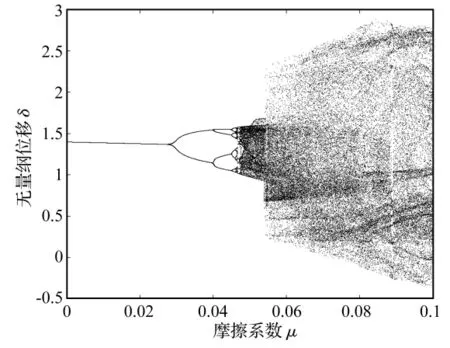
图17 位移－摩擦系数系数分岔图Fig.17 Displacement-friction coefficient bifurcation diagram

当摩擦系数μ=0.02时，系统响应为单周期非谐响应，如图18所示，时间历程图表现为单周期非简谐波，庞加莱截面上为单个点。当摩擦系数增大到 μ＞0.028时，系统响应开始发生倍周期分叉现象。当0.028＜μ≤0.04时系统为2周期次谐波响应，如图19所示。当0.04＜μ≤0.045时，系统为4周期次谐波响应如图20所示。当摩擦系数μ继续增大，系统响应依次为8、16…周期，最后通往混沌，如图21所示。

从上述分析可看出，齿面摩擦也是齿轮动力学中不可忽略的一个非线性因素。随着摩擦系数的增大，系统响应由单周期非谐响应经倍周期分叉进入混沌，当摩擦系数继续增大时，混沌区域逐渐扩大，系统进入幅值较大的混乱无序的振动状态。由于齿面摩擦力是一个非简谐的周期激励，它的存在进一步增强了齿轮传动系统的非线性特性。

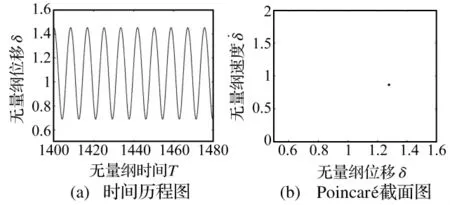
图18 单周期非谐响应（μ=0.02）Fig.18 Single period non-harmonic response

图19 2周期次谐波响应（μ=0.03）Fig.19 Two-period sub-harmonic response

图20 4周期次谐波响应（μ=0.045）Fig.20 Four-period sub-harmonic response

图21 混沌响应（μ=0.07）Fig.21 Chaotic response

3 结论

（1）建立了包含时变啮合刚度、啮合阻尼、齿面误差、齿面摩擦、齿侧间隙、轴承间隙等多种非线性因素，能较为全面描述正交面齿轮传动系统振动特性的非线性动力学模型。

（2）面齿轮传动系统动态响应特性非常复杂，随着啮合频率的变化，系统会呈现出单周期非谐响应、多周期次谐响应、拟周期响应及混沌响应。

（3）随着负载转矩的增大，系统响应由混沌经倍周期倒分岔进入单周期响应，齿轮副啮合状态由双边冲击、单边冲击过渡到无冲击状态。

（4摩擦系数较小时对系统动态响应特性影响不大，当其逐渐增大时，系统运动状态由单周期经倍周期分叉进入复杂无序的混沌运动。

［1］ Heath G F，Filler R R，Tan J.Development of face gear technology for industrial and aerospace power transmission［R］.NASA/CR－2002－211320，2002.

［2］ Litvin F L，Zhang Y，Wang J C，et al.Design and geometry of face-gear drives［J］.Journal of Mechanical Design，Transactions of the ASME，1992，114（4）：642－647.

［3］Litvin F L，Wang J C，Bossler J R B，et al.Application of face-gear drives in helicopter transmission［J］.Journal of Mechanical Design， Transactions of the ASME，1994，116（3）：672－676.

［4］ Litvin F L，Gonzalez-Perez I，Fuentes A，et al.Design，generation and stress analysis of face-gear drive with helical pinion［J］.Computer methods in applied mechanics and engineering，2005，194（36－38）：3870－3901.

［5］Litvin F L，Fuentes A，Zanzi C，et al.Design，generation，and stress analysis of two versions of geometry of face-gear drives［J］. Mechanism and Machine Theory， 2002，37（10）：1179－1211.

［6］李政民卿，朱如鹏.装配偏置误差对正交面齿轮传动接触特性的影响［J］.航空学报，2009，30（7）：1353－1360.

［7］李政民卿，朱如鹏.正交面齿轮齿廓的几何设计和根切研究［J］.华南理工大学学报（自然科学版），2008，36（2）：78－82.

［8］Zanzi C，Pedrero J I.Application of modified geometry of face gear drive［J］.Computer Methods in Applied Mechanics and Engineering，2005，194（27－29）：3047－3066.

［9］王晓笋，巫世晶，周旭辉，等.含侧隙非线性齿轮传动系统的分岔与混沌分析［J］.振动与冲击，2008，27（1）：53－56.

［10］ Li M，Hu H Y.Dynamic analysis of a spiral bevel-geared rotor-bearing system［J］.Journal of Sound and Vibration，2003，259（3）：605－624.

［11］ Gill-Jeong C.Nonlinear behavior analysis of spur gear pairs with a one-way clutch［J］.Journal of Sound and Vibration，2007，301（3－5）：760－776.

［12］孙智民，季林红，沈允文.负载对星型齿轮传动动态特性的影响分析［J］.机械科学与技术，2003，22（1）：94－97.

［13］靳广虎，朱如鹏，朱自冰，等.正交面齿轮传动系统的耦合振动分析［J］.机械科学与技术，2009，28（1）：124－128，132.

［14］陈广艳，陈国定，李永祥，等.含有面齿轮的传动系统动态响应特性研究［J］.航空动力学报，2009，24（10）：2391－2396.