薄壳单元法在接触物体间电磁力计算中的应用

刘慧娟， 傅为农

(1.北京交通大学电气工程学院，北京 100044;2.香港理工大学电气工程学院，香港特别行政区)

薄壳单元法在接触物体间电磁力计算中的应用

刘慧娟1， 傅为农2

(1.北京交通大学电气工程学院，北京 100044;2.香港理工大学电气工程学院，香港特别行政区)

针对在利用有限元法计算接触物体间电磁力时在物体接触表面没有积分单元可用的问题，首先，基于薄壳单元的思想，提出了一种在体积分和面积分之间确定附加薄壳单元的方法和一种在3D有限元法中利用附加薄壳单元精确计算接触物体间电磁力的方法，然后，基于虚功原理，推导了计算薄壳单元节点电磁力的T－Ω公式和雅可比矩阵表达式，并给出了计算物体接触表面分布电磁力的算法及其实现方法，最后将所提出的方法用于实例计算，并将3D有限元法计算结果与解析计算结果进行比较，证实所提出方法的有效性和正确性。

薄壳单元法;3D有限元法;接触面电磁力;虚功;T－Ω公式;雅可比矩阵;电磁设备;解析计算

0 引言

在电磁设备的设计与性能分析中，常采用有限元法(finite element method，FEM)，为了能更精确反映电磁设备内容的电磁过程，通常需要采用3D FEM进行瞬态电磁场或涡流场的计算［1］。3D有限元公式有两类:一类是采用矢量磁位(magnetic vector potential)A和标量电位(electric scalar potential)V的A－V公式，另一类是采用矢量电位T和标量磁位Ω的T－Ω公式，在低频电磁设备的设计与分析中，通常采用 T － Ω 公式［2－3］。

在低频电磁设备的有限元计算中，通常需要进行电磁力的计算［4－6］，而利用FEM计算某物体所受电磁力时，是在FEM的后处理中，通过沿该物体表面的一层单元进行体积分而计算得到的［7－9］。但是，在许多电磁设备中，常存在物体间的相互接触，此时，若需要利用FEM进行接触物体间电磁力的计算，就会出现在物体接触表面没有积分单元可用的问题，因此，利用通常的FEM后处理方法就不能计算接触物体间的电磁力。为此，必须在两物体的接触面构造出新的积分单元，才能进行电磁力计算。文献［10］首次提出在接触物体的表面添加附加薄壳单元来计算电磁力的思想，却并没有给出具体3D FEM的实现算法。

本文基于薄壳单元的思想，提出了一种在体积分和面积分之间确定附加薄壳单元的方法，然后，基于虚功原理，推导了利用局部磁能偏导数来计算3D有限元电磁力的T－Ω公式和雅可比矩阵表达式，并给出了计算物体接触表面分布电磁力的算法及其实现方法，该方法可用于计算接触表面局部和全局的电磁力，特别适合于永磁体(permanent magnet，PM)材料与其它物体接触的表面。最后将该方法用于计算两个PM物体接触面的电磁力值，并将FEM计算结果与文献［11］的解析计算结果进行了比较，证实了本文方法的有效性和正确性。

1 节点电磁力计算公式

在每个单元中，利用与位移s相关的磁共能的导数来计算各节点电磁力的公式为

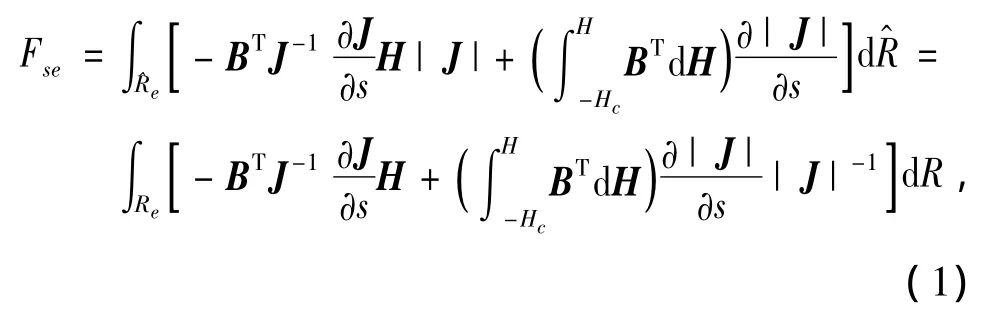
其中:B是磁密，H是磁场强度，Hc是永磁体(PM)的矫顽力，Re是自然坐标中的单元面积;R^e是参考坐标中的单元面积，J表示坐标变换之间的雅可比矩阵。

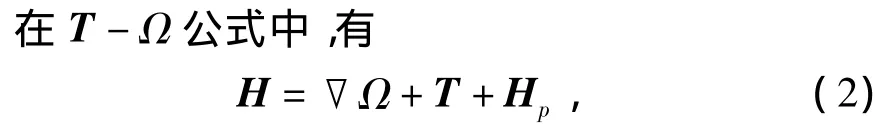
其中Hp是场源，为固体导体或多匝线圈中的已知全部电流或电流密度。

可将磁场效应Heff表示为

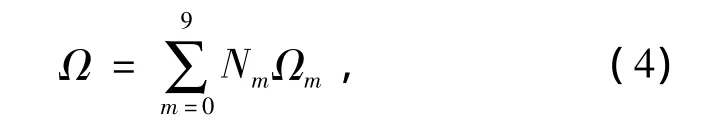
其中Nm是具有10个节点的二阶节点单元的形状函数。于是Ω为

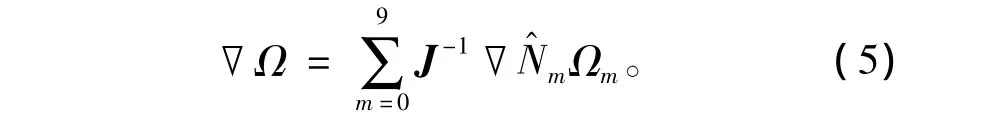
用一种新颖的四面体单元来计算磁标量Ω，即

在每个边界单元上的磁场强度H为

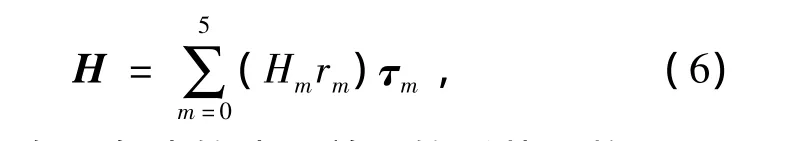
其中τm是具有6条边的边界单元的形状函数。

将式(2)、式(3)代入式(1)，有

全局坐标与局部坐标之间的关系为

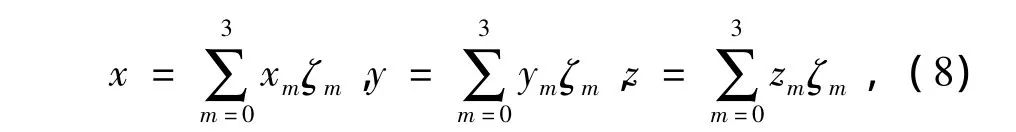
其中ζm是坐标的形状函数。雅可比矩阵为

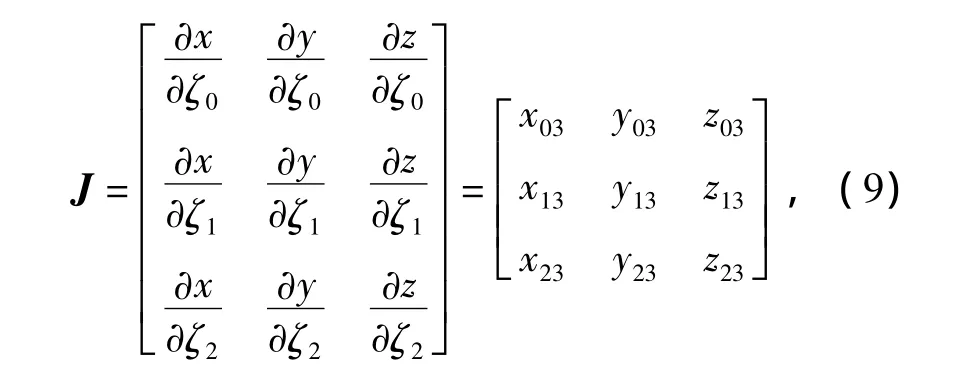
其中|J|=6V，V 是单元的体积，xij=xi－ xj，yij=yiyj，zij=zi－ zj，且 dxdydz=|J(x，y，z)|dζ0dζ1dζ2。假设节点i沿方向的位移为

2 接触物体间薄壳单元的处理

当两个物体相互直接接触，电磁力计算就需要沿接触表面进行面积分。为此，在接触面添加如图1(a)和图1(b)所示的三棱柱薄壳单元，且薄壳单元的高δ接近于0，薄壳单元的材料设为线性材料，则其磁导率等于真空磁导率，即μ=μ0。

磁场强度可表示为

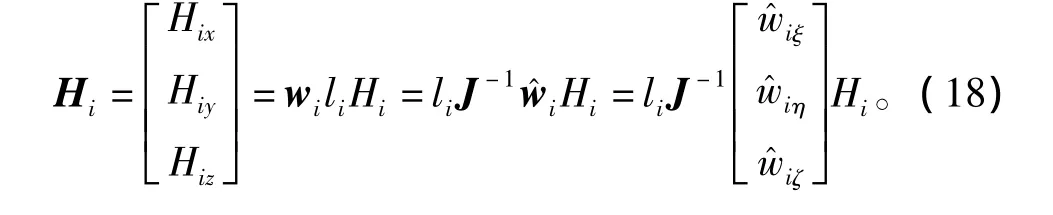
于是薄壳单元中的磁共能为

图1 三棱柱薄壳单元Fig.1 A triangular prism shell element

据文献［10］，将式(19)对位移s求偏导数，可得到单个薄壳单元的节点力为

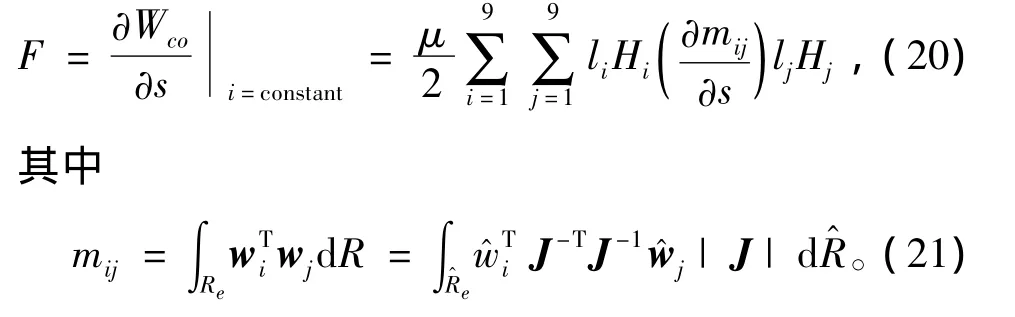
式(20)表明:通过保持边界上Hi的恒定，即电流恒定，可实现对电磁力的计算。

在式(21)中，只有雅克比矩阵与位移相关，参考单元的函数和面积均与位移无关，因此有

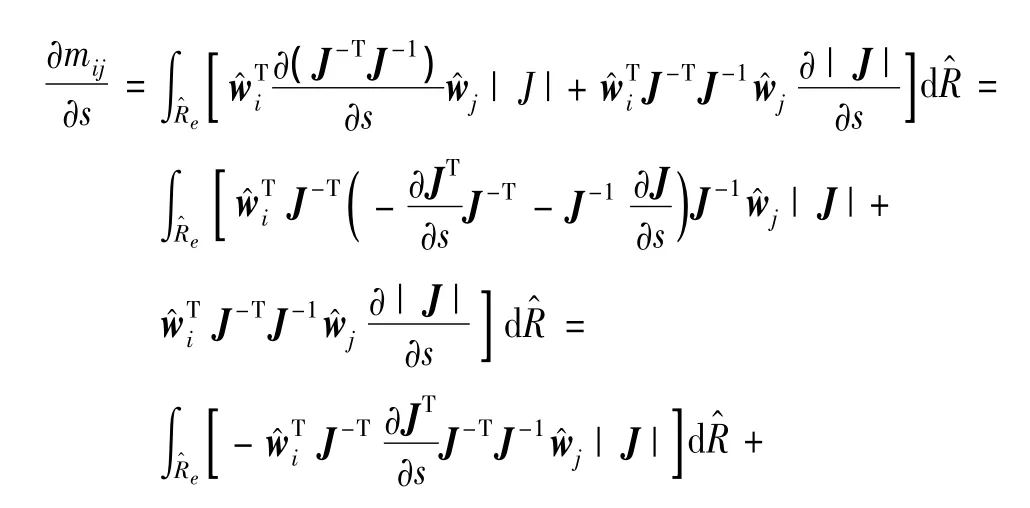
从自然坐标系(x，y，z)到参考坐标系(ξ，η，ζ)变换的雅可比矩阵为

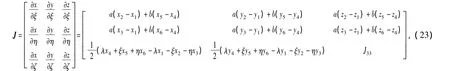
式(24)和式(25)中五面体单元的J和|J|可根据式(23)的基本雅克比矩阵推导得到。

3 算法的具体实现

在算法的实现过程中，需要在垂直方向设定两个标志位nf和nt，参考图2，将其定义为:nf=1表明该节点在需要计算电磁力的物体上，nf=0表明该节点不在需要计算电磁力的物体上。nt=－1表明该节点在需要计算电磁力物体的外表面，nt=1表明该节点在接触面上，nt=0表明该节点不在需要计算电磁力的物体上。

对每个单元定义

当ef＞0，且至少有一个节点的nt=－1时，则需要对该单元进行体积分。当et=3时，则需要对该单元进行面积分。

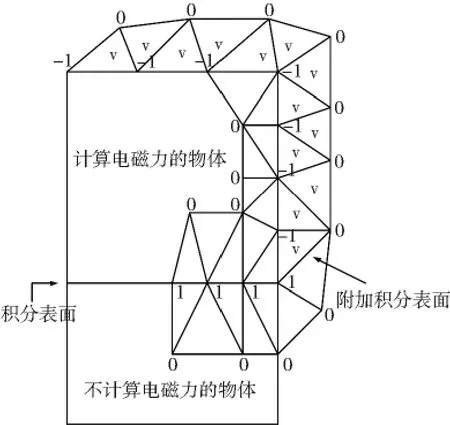
图2 各节点的标志位nt值示例Fig.2 An example of the flag nt

若将体积分改为面积分，就需要附加一个面积分单元。为简单起见，利用图2所示的3D示例来进行说明，并将薄壳单元按比例放大为如图3所示。当薄壳单元的高度δ不等于0时，则需要进行电磁力计算的物体将被一层体单元包围，薄壳单元3也包含在其中。于是，当薄壳单元的高度δ接近于0时，在体单元1和薄壳单元2之间就需要有另一个附加的薄壳单元3(如图3所示)。

图3 附加表面单元的示例Fig.3 An example of an additional surface element

在3D问题中，如图4所示，当四面体在体积分和面积分之间的分界面上(图4中每个四面体顶点上标注的数字为nt标志位值)时，存在3种情况，且只有情况1和情况2需要面积分。根据4个节点的标志位nt的数值，将很容易确定需要在哪个面上进行面积分。

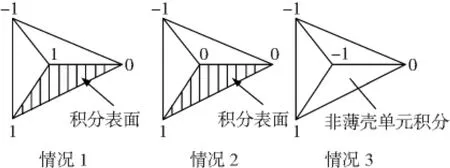
图4 四面体位于体积分和面积分之间的3种情况Fig.4 Three cases when the tetrahedron is in the interface between volume integration and surface integration

4 应用实例

为验证本文方法的可行性，将该方法用于实例计算，为进一步验证该方法的正确性，选用文献［11］中的两个相互接触的矩形永磁体的实例模型，并将本文的3D FEM计算结果与该文献中的解析计算结果进行比较。计算实例如图5所示，两永磁体沿z轴放置，具有相同的x和y坐标，其尺寸均为40 mm ×20 mm ×10 mm，且 Br=1.1 T，μ =μ0，当两永磁体在z轴方向的距离为0时，表明两个物体相互接触。

表1为两永磁体之间距离变化时，利用3D FEM计算的电磁力和文献［11］中解析计算的电磁力的数值，其中FEM的剖分单元数为83 666。从表1可见，有限元数值计算结果与解析计算结果有很好的一致性，特别是当两永磁体相互接触时，有限元计算结果与解析计算结果的差为0.041N，误差为0.022%，表明利用本文的方法能正确计算两永磁体接触面之间的电磁力。

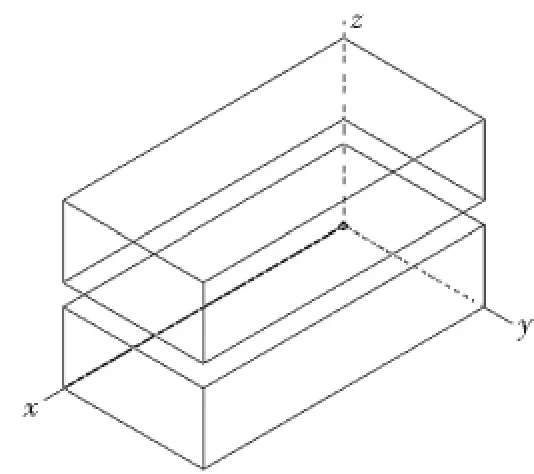
图5 两永磁体模型Fig.5 The model of two PM objects

表2为两物体相互接触时，采用不同的有限元剖分方法，计算的全部电磁力和附加薄壳单元电磁力的值。可见，当剖分网格较大时，附加薄壳单元的引入非常重要，并且，随着有限元剖分单元数量的增加，附加薄壳单元的电磁力逐渐减小，这是因为剖分单元数增多时，每个薄壳单元的尺寸都逐渐变小，因而对积分的贡献也就逐渐变小。

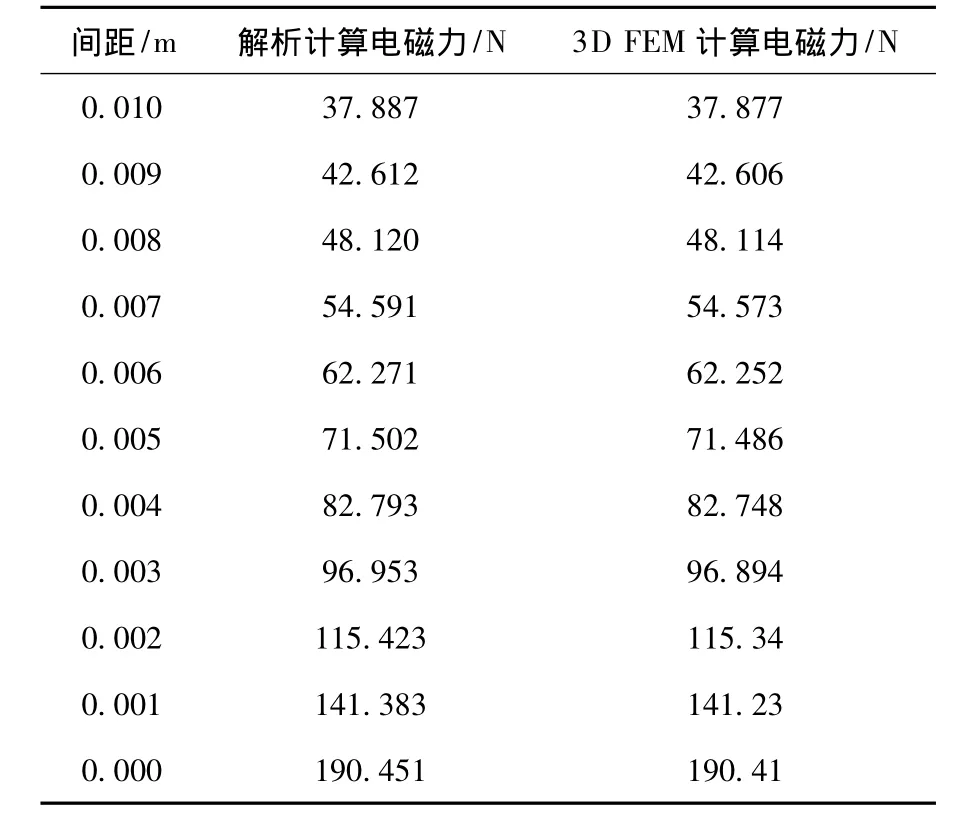
表1 3D FEM与解析计算结果的比较Table 1 Comparison of forces between two methods

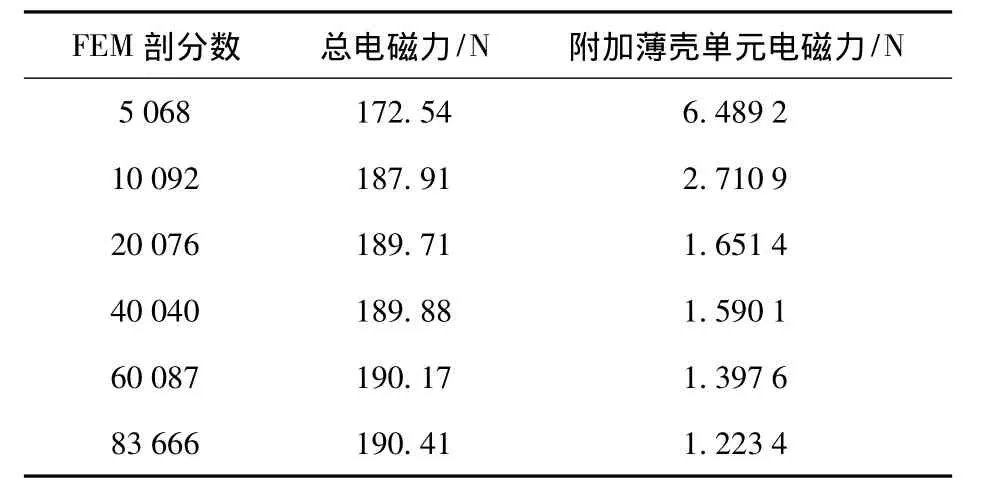
表2 不同剖分情况全部电磁力和附加薄壳单元电磁力值Table 2 The total force and the force of additional shell elements vs number of FEM elements

5 结论

本文提出了一种在3D FEM中利用附加薄壳单元计算接触物体间电磁力的方法。通过对应用实例的计算表明:

1)在3D FEM计算的后处理中，在体积分和面积分之间添加薄壳单元积分，可以精确计算接触物体间附加薄壳单元的节点力，其计算结果的精度与解析计算结果精度一致。

2)在利用3D FEM计算接触物体间电磁力时，通过附加薄壳单元，既可实现对接触物体全部电磁力的精确计算，也可实现对其局部电磁力的精确计算。并且，FEM网格剖分的数量和质量直接影响计算结果的精确度。

3)所提出的利用薄壳单元法计算接触物体间电磁力的T－Ω公式适用于其它材料类型的3D接触物体模型。当然，也可推导相应的3D A－V公式应用于FEM的后处理，进行接触物体间电磁力的计算。

［1］ STANCHEVA R D，IATCHEVA I I.3-D electromagnetic force distribution in the end region of turbogenerator［J］.IEEE Transactions on Magnetics，2009，45(3):1000 －1003.

［2］ ZHOU P，FU W N，LIN D，et al.Numerical modeling of magnetic devices［J］.IEEE Transactions on Magnetics，2004，40(4):1803－1809.

［3］ ZHOU P，LIN D，FU W N，et al.A general cosimulation approach for coupled field-circuit problems［J］.IEEE Transactions on Magnetics，2006，42(4):1051 －1054.

［4］ ZHU Z Q，WU L J，XIA Z P.An accurate subdomain model for magnetic field computation in slotted surface-mounted permanentmagnet machines［J］.IEEE Transactions on Magnetics，2010，46(4):1100－1115.

［5］ JIANG Hao，HUANG Xueliang，ZHOU Gan，et al.Analytical force calculations for high-precision planar actuator with Halbach magnet array［J］.IEEE Transactions on Magnetics，2009，45(10):4543－4546.

［6］ RAVAUD R，LEMARQUAND G，LEMARQUAND V.Force and stiffness of passive magnetic bearings using permanent magnets.part 1:axial magnetization［J］.IEEE Transactions on Magnetics，2009，45(7):2996 －3002.

［7］ COULOMB J.A methodology for the determination of global electromechanical quantities from a finite element analysis and its application to the evaluation of magnetic forces，torques and stiffness［J］.IEEE Transactions on Magnetics，1983，19(6):2514－2519.

［8］ REN Z，RAZEK A.Local force computation in deformable bodies using edge elements［J］，IEEE Transactions on Magnetics，1992，28(2):1212－1215.

［9］ FU W N，HO S L.Error estimation for the computation of force using the virtual work method on finite element models［J］.IEEE Transactions on Magnetics，2009，45(3):1388 －1391.

［10］ REN Z，CENDES Z.Shell elements for the computation of magnetic forces［J］.IEEE Transactions on Magnetics，2001，37(5):3171－3174.

［11］ AKOUN G，YONNET J-P.3D analytical calculation of the forces exerted between two cuboidal magnets［J］.IEEE Transactions on Magnetics，1984，20(5):1962 －1964.

(编辑:张诗阁)

Computation of electromagnetic force on the interface using shell element method

LIU Hui-juan1，FU Wei-nong2
(1.School of Electrical Engineering，Beijing Jiaotong University，Beijing 100044，China;
2.Department of Electrical Engineering，The Hong Kong Polytechnic University，Hong Kong，China)

In order to compute the electromagnetic force between two objects touching each other，an additional shell element is proposed and a simple method to determine the additional shell elements on the interface between volume integration and surface integration is also presented.A general formulation of nodal virtual work electromagnetic force computation between two objects touching each other for three-dimensional(3D)finite element analysis was presented.The T-Ω formulation and the Jacobian matrix were deduced and the implementation methodology was presented.An example with analytical solutions is used to verify the computed results.

shell element method;three-dimensional finite element method;interface electromagnetic force;virtual work;T-Ω formulation;Jacobian matrix;electromagnetic devices;analytical computation

O 242.21;TM 351

A

1007－449X(2012)08－0101－06

2012－04－01

香港理工大学科研项目(GU489)

刘慧娟(1967—)，女，博士，副教授，研究方向为电机及其控制、电机电磁场计算等;

傅为农(1962—)，男，博士，副教授，研究方向为电磁场数值计算的理论与应用、电机及特种电机的优化设计。

刘慧娟