混合磁悬浮球系统吸引子及稳定性研究

马凤莲， 江东， 张翔， 杨嘉祥

(哈尔滨理工大学电气与电子工程学院，黑龙江哈尔滨 150080)

混合磁悬浮球系统吸引子及稳定性研究

马凤莲， 江东， 张翔， 杨嘉祥

(哈尔滨理工大学电气与电子工程学院，黑龙江哈尔滨 150080)

为了避免磁悬浮球混沌运动，设计了永磁和电磁混合型磁悬浮球模型，推导了磁悬浮球的动力学方程，并建立了磁悬浮球系统的仿真模型。通过改变初始状态，得到不同初始条件下的磁悬浮球系统吸引子。混合型磁悬浮球系统具有单、双两类吸引子，双吸引子表现出较强的混沌特性，磁悬浮球围绕平衡点附近的波动较大，磁悬浮球由混沌运动状态向非混沌运动状态转变时，由双吸引子逐渐向单吸引子过渡，系统演变为具有周期特性的运动状态，再演变为相轨迹收敛于一个点，磁悬浮球处于较稳定的运动状态。仿真和实验结果表明，通过磁悬浮球吸引子的研究可了解混沌产生的初始区间，进而为设计中避开混沌区实现磁悬浮球的稳定运动提供了参考依据。

磁悬浮;初始状态;动力学方程;混沌运动状态;吸引子

0 引言

永磁和电磁混合型磁悬浮球系统有许多应用，如实现振动测量［1］、微风力测量［2］、速度及加速度测量［3－4］和风力发电［5］等。混合磁悬浮球系统在一定的条件下出现混沌现象，了解出现混沌的条件、混沌的特征以及系统如何从混沌状态到非混沌状态的过渡，可以更好地指导磁悬浮球系统中位移传感器的安装位置、控制器PD参数的设计以及磁悬浮球能够稳定的初始位置范围，扩大磁悬浮球运动的动态范围［6］，进而获得系统能够实现稳定的最佳条件，达到最佳控制和测量的目的［7］。在利用磁悬浮球系统实现测量的过程中，混沌运动特性将直接影响测量结果，对于磁悬浮球系统混沌状态的研究可以进一步实现小波去噪等数据处理［8］。

1 混合磁悬浮球系统构成及建模

永磁和电磁混合型磁悬浮球系统由电磁铁、磁悬浮球、位移传感器、环境红外光传感器、数据采集电路、控制电路、驱动电路构成，如图1所示。

图1 混合磁悬浮球系统Fig.1 Chart of hybrid magnetic levitation ball system

图1中，电磁铁线圈由直径为20 mm的铁心和缠绕直径为1 mm、匝数为1 341的铜导线构成。磁悬浮球由直径为140 mm的塑料球构成，塑料球上表面内部粘贴直径为22 mm、厚度为5 mm的永磁铁，电磁铁线圈与内部嵌有永磁铁的磁悬浮球构成混合磁悬浮球系统。永磁和电磁混合使用可以加大磁悬浮球的平衡范围，减小平衡点处通过电磁铁线圈的电流，系统接近于零功耗。位移传感器由红外发射和接收对管构成。环境红外光传感器由红外接收管构成，用于消除环境红外光对于测量结果的影响。

永磁和电磁混合型磁悬浮球系统模型如图2所示。

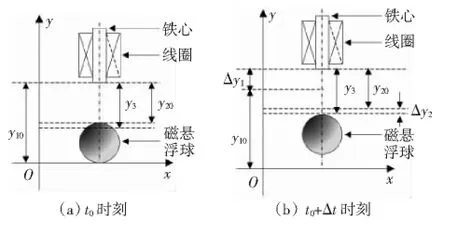
图2 混合磁悬浮球系统模型Fig.2 Model of hybrid magnetic levitation ball system model

图2(a)为t0时刻混合磁悬浮球系统的工作状态。y10为电磁铁的初始位置，y20为磁悬浮球的初始位置，y3为位移传感器的安装位置。图2(b)为t0+Δt时刻混合磁悬浮球系统的工作状态。用y1=y10+Δy1表示t0+Δt时刻电磁铁的位移，y2=y20+Δy2表示t0+Δt时刻磁悬浮球相对于电磁铁的相对位移，光电位移传感器相对于电磁铁的距离y3固定不变。

将磁悬浮球放于平衡点附近，当磁悬浮球所受重力大于电磁铁提供的磁力时，磁悬浮球向下运动，磁悬浮球遮挡光电位移传感器面积减小，红外接收管接收更多的来自红外发射管的红外光，其电压信号输出至控制电路，通过驱动电路使电磁铁线圈电流加大;反之，当磁悬浮球所受重力小于电磁铁提供的磁力时，磁悬浮球向上运动，磁悬浮球遮挡光电位移传感器面积增大，红外接收管接收较少的来自红外发射管的红外光，控制电路通过驱动电路使电磁铁线圈电流减小，且控制电路内含微分电路，最终使磁悬浮球在平衡点附近悬浮。

磁悬浮球与电磁铁之间气隙中的磁场分布均匀时，磁悬浮球所受磁力［9］可表示为

式中:c为系数;i为电磁铁电流。改变电磁铁电流i和磁悬浮球相对于电磁铁的相对位移y2使磁悬浮球达到平衡，实测平衡点处电流i与电磁铁的位移y2之比为常数，说明式(1)中的系数c为一常数。实测磁悬浮球所受磁力与电流和位移的关系如图3所示。

图3(a)为固定磁悬浮球位移y20=0.023 m时磁悬浮球所受磁力与电流的关系;图3(b)为固定电磁铁电流i=0.254 A时磁悬浮球所受磁力与磁悬浮球位移的关系。计算得到式(1)中的系数c=0.016。

图3 磁力与位移和控制电流关系Fig.3 Relationship between magnetic force and displace or controlling current

根据牛顿第二定律得到

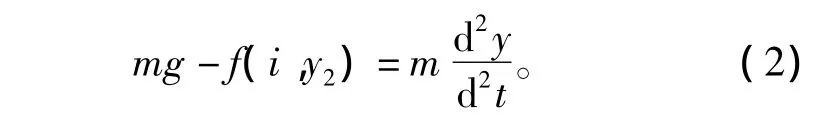
式中:m为磁悬浮球质量;y为磁悬浮球的位移，其表达式为

当电磁铁相对于坐标不动时y1固定不变，式(2)变为

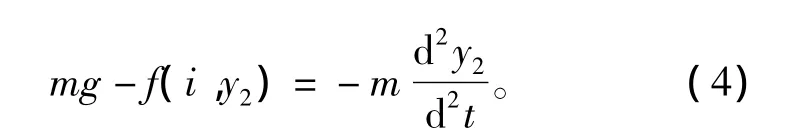
当电磁铁相对于坐标运动时，y1随时间变化，当y1振动频率较高时，y2的频率特性与y1的频率特性近似相同，可以实现对外界振动的测量［10］。

2 混合磁悬浮球系统仿真模型设计

为实现磁悬浮球稳定，控制方法采用超前控制，设计比例、微分控制电路，磁悬浮球系统的控制电路如图4所示。

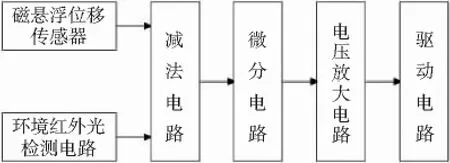
图4 磁悬浮球系统控制电路Fig.4 Control circuit of magnetic levitation ball system

图4中，减法电路将磁悬浮位移传感器的输出信号与环境红外光检测电路的输出信号相减，差值送入比例、微分控制电路，微分电路由RC电路构成，通过电压放大电路和驱动电路实现对电磁铁电流的控制。

混合磁悬浮球系统仿真模型如图5所示。图5上半部分表示磁悬浮球的动力方程，下半部分为控制系统电流与位移变化的控制关系。选用的光电位移传感器的电压转换灵敏度CI=3 kV/m。设u1为磁悬浮球位移传感器的输出电压，u2为环境红外传感器的输出电压，减法电路输出为

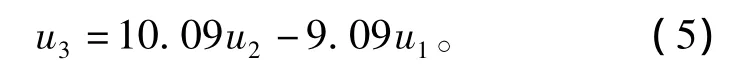
微分电路传递函数为

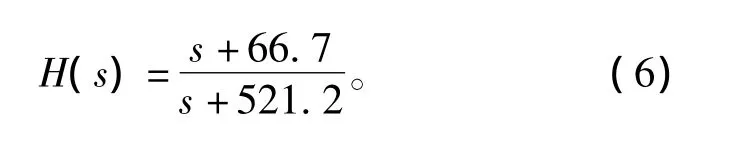
电压放大电路放大系数k3=247.67，电流放大驱动电路变换系数k4=1/30 000 s，实测磁力系数k5=0.04。由此实现控制电路输出电流随时间的变化量为

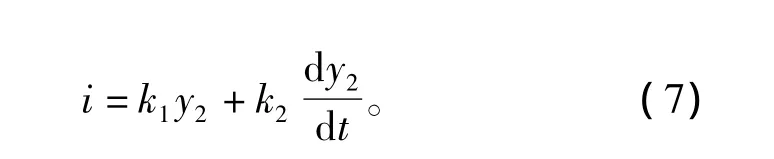
式中:k1为比例系数，k1=499.4;k2为微分系数，k2=7.5。

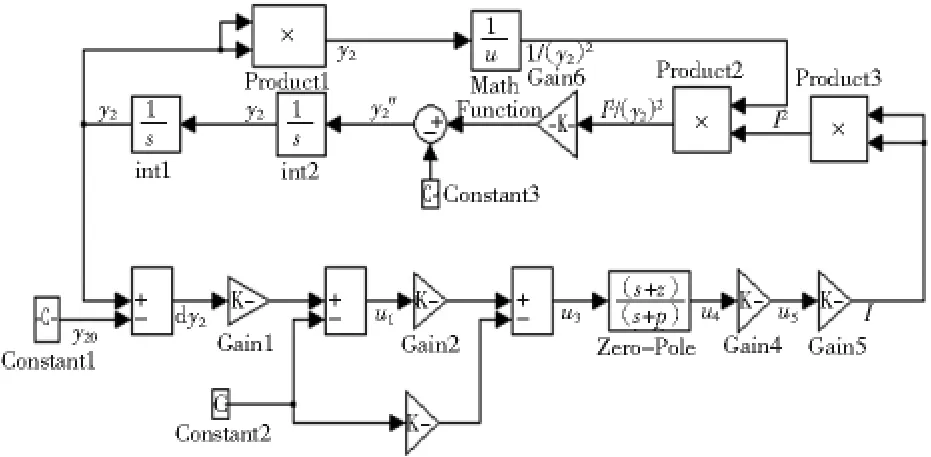
图5 磁悬浮球系统仿真模型Fig.5 Simulation model of magnetic levitation ball system

3 混合磁悬浮球系统吸引子类型和产生条件

磁悬浮球混沌运动有两种吸引子，即单吸引子和双吸引子。零极点过小时混合磁悬浮球系统具有双吸引子，系统处于混沌运动状态;加大零极点时系统具有单吸引子，系统的混沌特性减弱。

仿真数据为:y3=0.023 m;y20=0.025 5 m;CI=3 kV/m;k4=1/30 000 s;力系数为0.04。PD参数即零点Z0=－10，极点P0=－100时，磁悬浮球相轨迹如图6(a)所示;PD参数即零点Z0=－20，极点P0=－200时，磁悬浮球相轨迹如图6(b)所示。

由图6可知，零、极点较小时为双吸引子，零、极点较大时为单吸引子。实测的单、双吸引子对应的波形如图7所示。

由图7可知，双吸引子时磁悬浮球随时间变化波形的向上的峰值和向下的峰值均存在，说明其混沌特性较强，此时磁悬浮球的总波动范围较大;单吸引子时磁悬浮球随时间变化波形的峰值基本出现在波形的下方，说明其混沌特性在减弱。

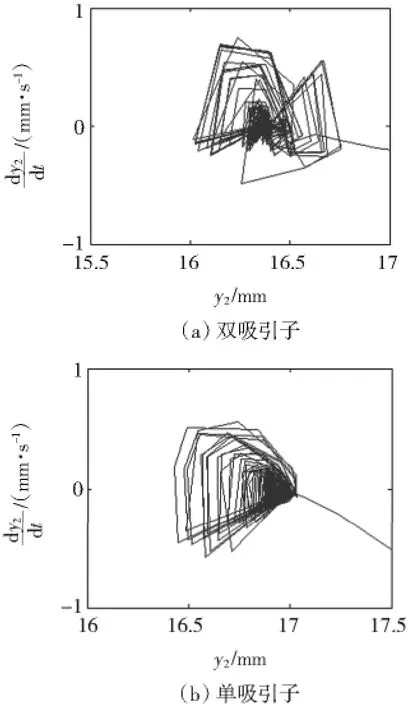
图6 单、双吸引子对应的相轨迹Fig.6 Phase trajectory corresponding single and double attractor

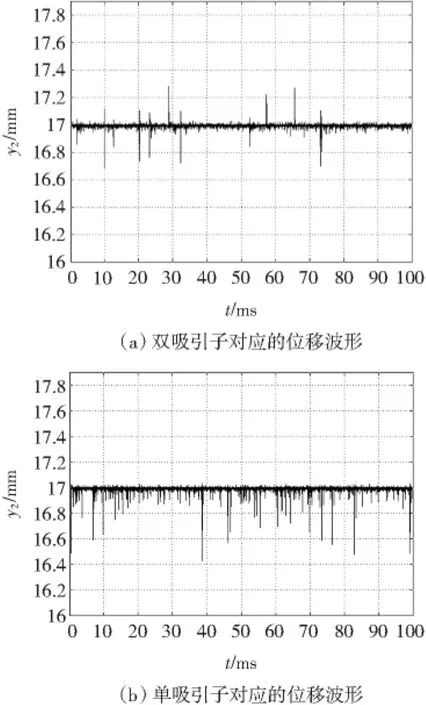
图7 单吸引子与双吸引子对应的磁悬浮球位移Fig.7 Displacement of magnetic levitation ball corresponding single and double attractor

4 混沌状态向稳定状态的转化过程和稳定范围及最佳平衡条件

只改变控制系统的PD参数，零、极点由小到大增加时，磁悬浮球的混沌特性逐渐减弱。零、极点由小到大变化时磁悬浮球相轨迹如图8所示。

图8(a)为双吸引子情形，磁悬浮球处于混沌运动状态;图8(b)为单吸引子情形，磁悬浮球的混沌运动特性在减弱;由图8(c)可知，磁悬浮球由混沌运动状态逐步演变成周期型的运动状态;由图8(d)可知，磁悬浮球的周期运动状态被打破，近似椭圆形的相轨迹运动范围逐步在缩小，并向一个点收缩，磁悬浮球向非混沌的稳定状态过渡;图8(e)和图8(f)的相轨迹已经逐步变成向一个点收敛的情形，磁悬浮球由最初的混沌运动状态变成非混沌的稳定运动状态。

决定磁悬浮球稳定的因素很多，包括位移传感器的安装位置、光电传感器灵敏度、电压增益、环境红外光、电压放大倍数、微分电路PD参数、电流放大倍数、电磁铁电流与力的系数以及磁悬浮球初始位置等。为便于研究影响磁悬浮球稳定的主要因素，以位移传感器的安装位置、微分电路PD参数和磁悬浮球初始位置为变化量而其他因素固定不变。图9为磁悬浮球稳定平衡的条件与位移传感器的安装位置、微分电路PD参数和磁悬浮球初始位置的关系。

图9中，y20为磁悬浮球的初始位置，y3为位移传感器的安装位置。图9中显示的区域为磁悬浮球稳定平衡的区域。图10为在不同PD参数下，磁悬浮球稳定平衡的条件与位移传感器的安装位置和磁悬浮球初始位置的关系。

图10中，y20和y3的含义与图9相同。通过图10可以方便地比较不同的PD参数、位移传感器的安装位置和磁悬浮球初始位置对磁悬浮球稳定平衡的影响。

由图10可知:1)零点Z0较小时对应的稳定区的位移传感器的安装位置y3上限较大，可获得磁悬浮球较大的动态范围，应取较小的Z0;2)零点Z0较小时，磁悬浮球平衡的初始位置y2范围较小，为使磁悬浮球平衡的初始位置的范围较宽，应取较大的Z0。既要稳定又要有大的动态范围，混合磁悬浮球系统的最优参数为:Z0=－40;P0=－400;y3=－0.023 m;y20= －0.025 5 m。

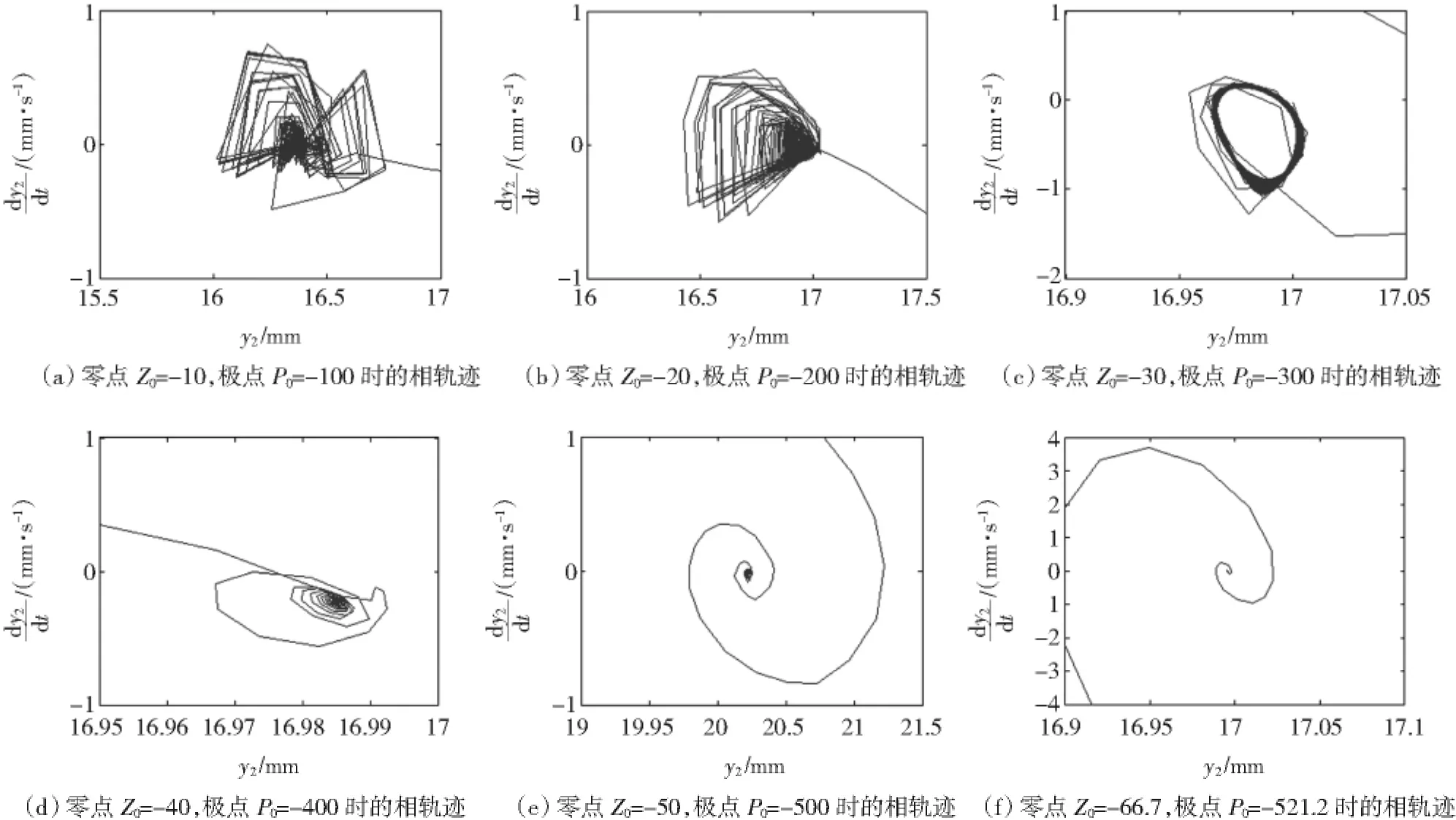
图8 不同PD参数对应的相轨迹Fig.8 Phase trajectory corresponding different PD parameters

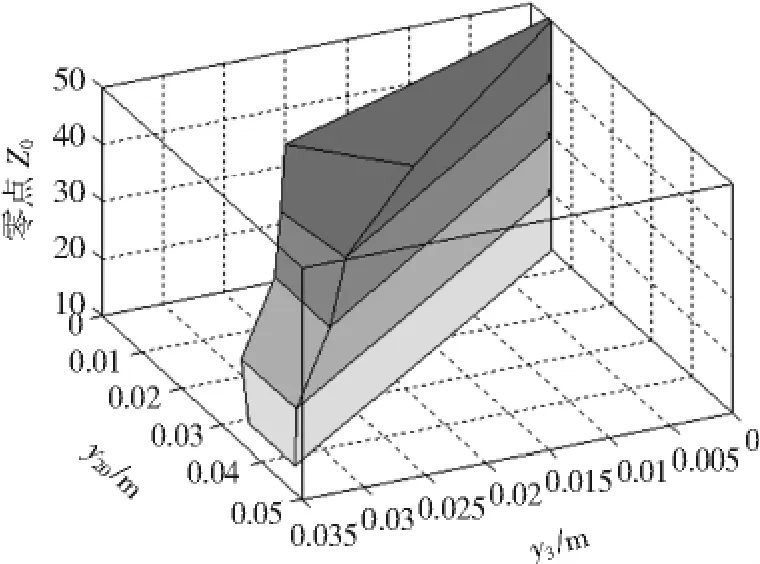
图9 零点Z0、y20和y3对应的三维稳定区域Fig.9 Three-dimensional stability region corresponds to Z0，y20and y3

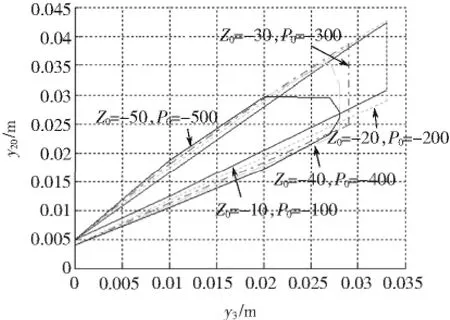
图10 不同PD参数对应的稳定区域Fig.10 Stability regions corresponding to different PD parameters

5 外加干扰时磁悬浮球位移

为了验证混合磁悬浮球系统工作的稳定状况，外加干扰源使混合磁悬浮球系统处于振动中。采用HEV－20型高能激振器作为干扰源，该激振器是一种电动式变换器，可将电能转换为机械能，对试件提供激振力。激振器最大允许激振力为20 N，最大振幅为±5 mm，频率范围为0～5000 Hz且连续可调。激振器置于磁悬浮球模型之上，激振器振动引起磁悬浮球模型一起振动。在激振频率范围0～5000 Hz内磁悬浮球均能稳定工作，其中振动信号的振幅为1 mm，频率为60 Hz。在系统最佳参数下，实测的磁悬浮球位移信号如图11所示。

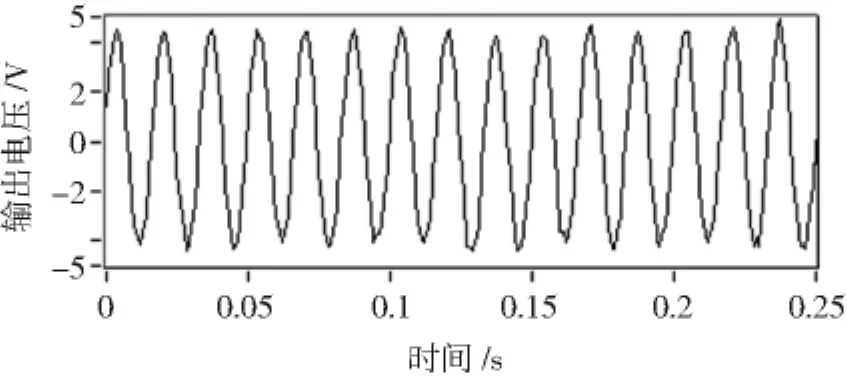
图11 激振器为60 Hz时磁悬浮球的位移Fig.11 Displacement of magnetic levitation ball when vibration exciter frequency is 60 Hz

由图11知，所设计的磁悬浮球系统远离混沌区，避免了混沌运动出现，实测数据表明系统的稳定性良好。

6 结语

混合磁悬浮球系统混沌运动有两种吸引子，零、极点过小时混合磁悬浮球系统具有双吸引子，磁悬浮球双向振动剧烈，系统处于较强的混沌运动状态;加大零、极点时系统具有单吸引子，磁悬浮球只单向振动剧烈，系统的混沌特性减弱;随着零、极点逐渐增加，磁悬浮球由混沌运动状态至稳定状态经历了双吸引子、单吸引子、周期型相轨迹、椭圆形相轨迹，最后相轨迹收缩至一个点。零点Z0较小时对应稳定区的位移传感器安装位置y3上限较大，零点Z0较大时，磁悬浮球平衡的初始位置y2范围较大。为避免磁悬浮球处于混沌运动状态，使磁悬浮球有较大的动态范围及能实现稳定的磁悬浮球初始位置较宽，通过仿真获得零、极点最优设计值。仿真和实验结果表明，通过对磁悬浮球吸引子的研究可以了解混沌产生的初始区间，避开混沌区以实现磁悬浮球的稳定运动，可作为磁悬浮球系统设计的重要参考。

［1］ 江东，杨嘉祥，姜狄，等.基于磁悬浮技术惯性式振动测量方法研究［J］.振动工程学报，2010，23(5):554－559.

JIANG Dong，YANG Jiaxiang，JIANG Di，et al.Research on inertia vibration measure method based on magnetic-suspending technique［J］.Journal of Vibration Engineering，2010，23(5):554－559.

［2］ 程启明，程尹曼，汪明媚，等.风力发电中风速测量技术的发展［J］.自动化仪表，2010，31(7):1－4.

CHENG Qiming，CHENG Yinman，WANG Mingmei，et al.Development of wind speed measuring technologies in wind power gemeration［J］.Process Automation Instrumentation，2010，31(7):1－4.

［3］ 迟晓珠，金鸿章，王劲松.压阻式复合惯性加速度传感器的研究［J］.仪器仪表学报，2003，24(z2):262－263.

CHI Xiaozhu，JIN Hongzhang，WANG Jinsong.Research on piezoresistive complexed inertial accelerometer［J］.Chinese Journal of Scientific Instrument，2003，24(z2):262 －263.

［4］ 温淑慧.一种电容式加速度传感器设计的研究［J］.传感技术学报，2005，18(2):329－332.

WEN Shuhui.Study of capacitive acceleration transducer design［J］.Chinese Journal of Sensors and Actuators，2005，18(2):329－332.

［5］ 杨国良，李惠光.磁悬浮无刷直流风力发电机Fuzzy PID分级控制研究［J］.机床与液压，2008，36(7):276－278.

YANG Guoliang，LI Huiguang.The research on fuzzy switch fuzzy-PID controller for wind driven-maglev brushless DC generator［J］.Machine Tool＆ Hydraulcs，2008，36(7):276－278.

［6］ 孙桥，于梅.比较法相位型振动校准系统的研究和实现［J］.计量学报，2005，26(2):142－145.

SUN Qiao，YU Mei.Development of the vibration complex sensitivity calibration system based on compensation method and virtual instrument technology［J］.Actametrologica Sinica，2005，26(2):142－145.

［7］ 姚宏，郭雷，徐健学.高维磁悬浮控制系统混沌与控制器设计研究［J］.仪器仪表学报，2003，24(2):175－178.

YAO Hong，GUO Lei，XJianxue.The research on the controller’s design and chaos for a multidimensional magnetic levitation control［J］.Chinese Journal of Science Instrument，2003，24(2):175－178.

［8］ 汤宝平，何启源，蒋恒恒，等.利用小波去噪和HHT的模态参数识别［J］.振动、测试与诊断，2009，29(2):197－200.

TANG Baoping，HE Qiyuan，JIANG Hengheng，et al.Modal parameter identification based on hilbert huang transform and wavelet de-noising［J］.Journal of Vibration Measurement ＆ Diagnosis，2009，29(2):197－200.

［9］ 上官霞南，江东，顾玉武，等.混合磁悬浮球系统变参数PID控制仿真［J］.哈尔滨理工大学学报，2007，14(2):31－34.

SHANGGUAN Xianan，JIANG Dong，GU Yuwu，et al.Simulation of a variable parament PID controller for hybrid magnetic levitation ball system［J］.Journal of Harbin University of Science and Technology，2007，14(2):31－34.

［10］ 江东，高颖，杨嘉祥.磁悬浮效应检振系统设计［J］.电机与控制学报，2008，12(3):343－347.

JIANG Dong，GAO Ying，YANG Jiaxiang.Vibration measuring principle and system based on magnetic levitation effect［J］.E-lectric Machines and Control，2008，12(3):343 －347.

(编辑:于双)

Attractors of hybrid magnetic levitation ball system and stability research

MA Feng-lian， JIANG Dong， ZHANG Xiang， YANG Jia-xiang
(College of Electrical＆ Electronic Engineering，Harbin University of Science and Technology，Harbin 150080，China)

In order to avoid magnetic levitation ball in the chaotic region，the model of permanent magnet and electromagnet hybrid magnetic levitation ball system was designed，the dynamic equation of magnetic levitation ball was deduced，and the magnetic levitation system simulation model was set up.The different attractors were obtained by changing the initial states.The simulation results show that the hybrid magnetic levitation ball system designed has single and double two types of attractors.The double attractors have stronger chaotic performance and the magnetic levitation ball has greater fluctuation around the equilibrium point.The attractor is gradually from double attractors to single attractor in magnetic levitation ball from chaotic station transition to non-chaotic state，the magnetic levitation ball becomes a cyclical nature of the motion state and it gradually evolves to a point of phase trajectories when the system presents a stable state.Simulation and test show that the chaos generated by the initial region can be understood by studying the magnetic levitation ball attractors，which provides a reference design basis to avoid the chaotic region and to achieve magnetic levitation ball stable movement.

magnetic levitation;initial state;dynamic equation;chaos state of motion;attractors

TM 571.6

A

1007－449X(2012)08－0011－06

2010－12－09

国家自然科学基金(50777014);高等学校博士学科点专项科研基金(20040214003)

马凤莲(1981—)，女，博士研究生，讲师，研究方向为振动能量存储;

江 东(1960—)，男，博士，教授，研究方向为磁悬浮检振理论及电工理论新技术;

张 翔(1988—)，男，硕士研究生，研究方向为非线性控制、鲁棒控制、智能控制;

杨嘉祥(1938—)，男，教授，博士生导师，研究方向为高电压及电工理论新技术。

马凤莲