变频器驱动异步电机振动频谱特征分析

李文， 赵慧敏， 邓武

(大连交通大学软件学院，辽宁大连 116028)

变频器驱动异步电机振动频谱特征分析

李文， 赵慧敏， 邓武

(大连交通大学软件学院，辽宁大连 116028)

为提出一种更加有效的电机振动抑制算法，对电机振动频谱特性进行讨论。介绍了异步电机调速系统振动数据采集单元以及不同运行状态下的电机振动数据采集，给出了调压器调压和变频器变频调速2种情况下不同转速的电机振动频谱图和转速谱图。通过这些谱图，分别对电机振动特征、变频器载波频率对电机振动特征的影响进行了对比分析。谱图分析表明，采用变频器驱动异步电机时，一阶转频引起的强迫振动与自由振动波形会发生畸变，且电机振动峰值增大。随着变频器载波频率的增加，电机振动幅值将显著降低。变频器引入的高阶振动谐波转矩使得电机的振动特征更加复杂。电机振动频谱特征分析为电机振动抑制算法设计与算法评价提供了基础。

异步电机;变频器;振动频谱;谐波分析

0 引言

用变频器驱动异步电机实现交流调速在工业领域被广泛应用。目前最常用的变频器主电路为交—直—交形式，在整流回路中接有大电容，输入电流的波形不是正弦波;在逆变输出回路中输出电压信号是受PWM(pulse width modulation)载波信号调制的脉冲波形，有较多的高次谐波含量。变频器中含有的各次时间谐波与电磁空间谐波相互作用，形成各种电磁激振力［1－2］。当电磁力波的频率和电动机机体的固有振动频率一致或接近时，将产生共振现象，从而加大噪声。在要求调速范围比较大的情况下，电机将工作在一个较宽的频率范围，这会使得各种电磁力波的频率较难避开电动机的各构件的固有振动频率。因此，当普通异步电机采用变频器调速时，会使原本由电磁、机械、通风等因素所引起的振动和噪声变得更加复杂。

通常，异步电机调速系统的控制器设计，主要考虑其速度的跟踪特性和稳定性。本文研究的目的是通过对一种变频器驱动的异步电机振动频谱特征分析，可以为从电机振动特征角度来评价控制器性能、研究电机振动抑制策略及算法提供有效的、针对性强的参考依据。同时，也为此类系统的振动抑制方法提供一种思路。文中首先根据变频器驱动的异步电机谐波理论，讨论了变频器输出电压谐波和电机谐波转矩问题;然后，简要介绍了电机振动测试平台和振动数据采集实验，对变频器驱动和调压器调压控制下的电机振动频谱进行了对比分析;最后，讨论了变频器载波频率变化对电机振动的影响。

1 变频器驱动的异步电机谐波分析

1.1 变频器输出电压谐波分析

对于低压变频器主要采用交—直—交主电路，其控制方式多选用电压正弦波脉宽调制，即SPWM(sinusoidal PWM)。变频器通常由整流、中间直流环节、逆变和控制4个部分组成。首先通过三相桥式不可控整流器将工频交流电源转换成直流电源;经中间直流环节滤波、储能后，在逆变输出回路中输出受载波信号调制的脉冲电流，他可被分解为基波和其他高次谐波两部分。所讨论的变频器驱动异步电机系统中，变频器为交—直—交电压源型SPWM变频器，其调制信号生成方法为双极性调制。下面给出变频器输出电压的谐波分析。

在双极性三角波调制情况下，设一个正弦波周期内有N个脉冲，为了保证正、负半周对称，半周内以π/2为对称，N为奇数，且为3的倍数。为分析简便起见，将导通时间、间隔时间都分别看成是一个脉冲，则在半个正弦波(π)内有N个脉冲。这样每个脉冲中心点所对应的角度为

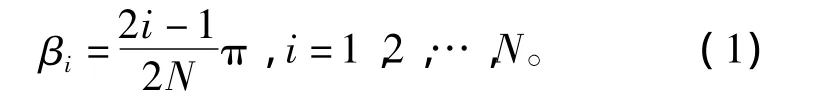
设UMm为调制波峰值，Ucm为载波峰值，则每个脉冲宽度可表达为［3］

为了获得较好的正弦输出波形，可采用分段同步调制方式或多电平逆变器多载波调制策略［3］。因此分析可按同步调制进行。由于在正、负半周中，波形对称于π/2轴，且原波形为镜对称，所以在进行傅里叶级数展开时，恒定分量和偶次谐波分量均为零，即在傅里叶展开式中Ak=0，仅包含奇次谐波分量。从而相电压可表达为

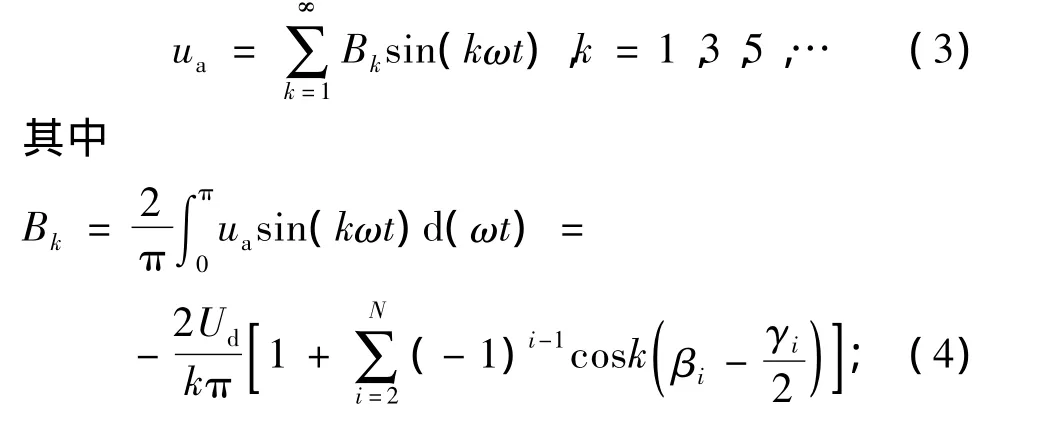
Ud为逆变环节直流侧电压。由式(4)可求得相电压ua中的基波电压峰值及k次谐波电压峰值分别为［3］

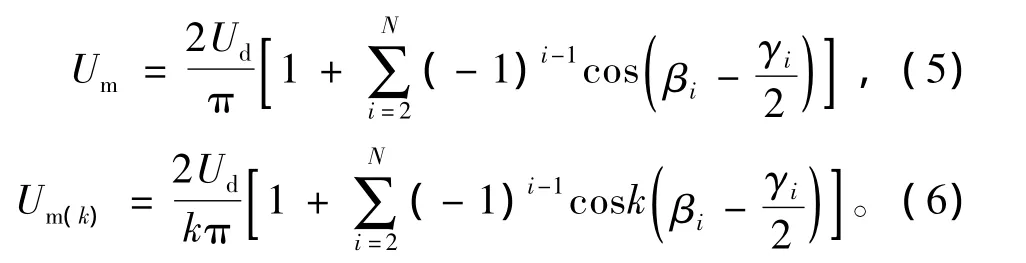
以上计算表明，变频器主回路输出电压峰值与调制系数m成正比。由式(3)可写出线电压的傅里叶表达式为

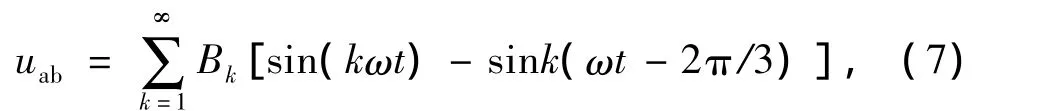
其中，k=1，3，5，…。从式(7)可看出，当 k为3 的整数倍时，［sin(kωt)－sink(ωt－2π/3)］=0，这说明在线电压中不含有3的整数倍次谐波，故谐波次数可用 k=6j±1 表示，加号对应 j=0，1，2，…，减号对应j=1，2，…。运用三角函数和差化积公式，则有

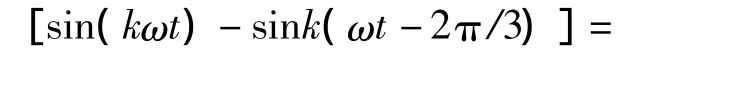
根据式(11)可知，对输出的相电压和线电压基波和谐波幅值均可采用式(5)和式(6)进行计算和分析。

1.2 异步电机谐波转矩分析

异步电机在变频器驱动下，电压谐波会在气隙中产生一系列时间和空间谐波磁势，从而产生附加的谐波转矩。根据产生的具体原因和性质不同，这些附加的谐波转矩可分为异步谐波转矩、同步谐波转矩和振荡谐波转矩。

1.2.1 异步与同步谐波转矩

所谓异步谐波转矩是指空间存在某一方(如定子)产生的一个谐波旋转磁场，他在另一方(如转子)会感应产生一个极数相同、转速和转向一致的谐波旋转磁场，两者相互作用所产生的谐波转矩，又称为稳定谐波转矩［7－9］。也就是说，异步(或稳定)谐波转矩是由气隙谐波磁通和由他感应出的转子电流谐波相互作用而产生的。这些谐波转矩可以采用相应的谐波等值电路求解，可得k次稳定谐波转矩值为［8］

式中，n1为基波磁场旋转速度，n为转子的实际转速;当谐波磁势正转时用“－”号，反转时用“+”号［6］。由基波转差率，可求得，将

所谓同步谐波转矩是指在定、转子两边存在的两个相对独立的、具有相同极数和相同转向的谐波磁场，当转子转速为某一特定速度时，这两个磁场在空间同步、且相对静止，则会产生同步谐波转矩，一旦转子速度改变，该同步谐波转矩则自动消失。同步附加转矩会使电机的合成转矩发生突变，例如当电机转速n=0时出现同步附加转矩，则会出现堵转(称为同步堵转)，使电机无法启动［4］。然而对于变频器驱动的异步电机，由于其具有软启动特性，故在启动过程中不会出现同步堵转情况［5］。

1.2.2 振动谐波转矩

在研究附加谐波转矩对电机运行影响问题时，重点关注的是振动谐波转矩。振动谐波转矩又称为谐波脉动电磁转矩，它是由不同次的气隙谐波磁通和转子谐波电流相互作用产生的。振动谐波转矩的方向，半周为正，另半周为负，因而平均值为零［10］。但是，在任意时刻，这些振动谐波转矩对电机运行会产生作用，而有较大影响的振动谐波转矩是由转子谐波电流与基波旋转磁通产生的，其中幅值较大的为5、7、11、13各次谐波电流所产生的磁场与基波电流所产生的磁场相互作用引起的振动谐波转矩［9］。

设基波磁场旋转角频率为ω1，电机旋转角频率为ω，并与基波磁场同向旋转，则基波的转差率为s=(ω1－ω)/ω1。许多文献给出了5次和7次谐波电流所产生的旋转磁场相对于基波旋转磁通的角频率分别为［4，8－9，11］

从而证明了5次和7次谐波电流磁场与基波磁场相互作用所产生的振动谐波转矩频率均为6倍转子基波电流的频率。由式(15)可知，式(16)和式(17)中的(ω －5sω1)和(ω +7sω1)表达了5次谐波电流所产生的振动谐波转矩为制动转矩，这个转矩企图使转子旋转减速;而7次谐波电流所产生的振动谐波转矩为拖动转矩，这个转矩企图使转子旋转加速。

文献［10］以5次和7次谐波为例，具体计算了各相基波磁通在转子中所感应的电势E'2与转子中5次谐波电流I'25和7次谐波电流I'27相互作用所形成的振动谐波转矩，求得了三相的合成振动谐波转矩分别为

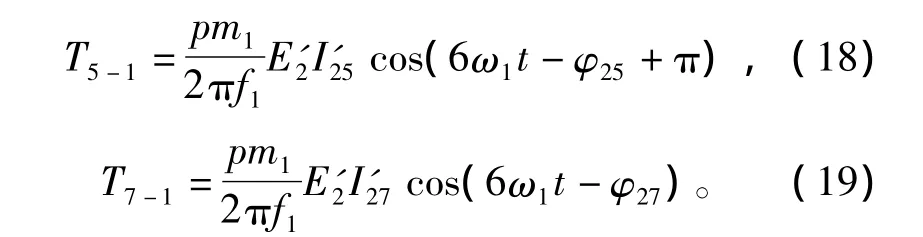
式中，相位差为π，说明这两个振动谐波转矩分别为制动和拖动转矩，且二者频率均为6sω1，从而得出了与式(16)和式(17)同样的结论。

2 电机振动数据采集

为分析异步电机在变频器驱动情况下的电机垂向振动特性，对电机—发电机组进行了振动测试实验，布置了4个加速度传感器，分别用来测试电机的垂向、水平、机座和发电机垂向的振动，具体位置如图1所示。表1和表2分别给出了电机、发电机、变频器及振动加速度传感器的相关参数。为更有效地分析变频器驱动异步电机的振动特征，分别采集了在调压器调压控制和变频器开环驱动时，5种不同转速下的电机振动数据;为了讨论变频器不同载频对电机振动的影响，设计了在载频分别为3 kHz和15 kHz情况下的电机振动数据采集实验。振动数据的采集是在振动测试与分析平台上进行的，其数据采集环节由NI公司生产的USB2.0即插即用型8槽NI CompactDAQ机箱底座NIcDAQ－9172和4通道C系列动态信号采集模块NI－9234组成。在振动数据采集中，为了能够比较准确地反映0～4000 Hz频段的电机振动情况，其采样频率设为12.8 kHz。

图1 传感器位置图Fig.1 The sensor location figure

表1 电机－发电机组参数Table 1 Parameters of motor-generator group

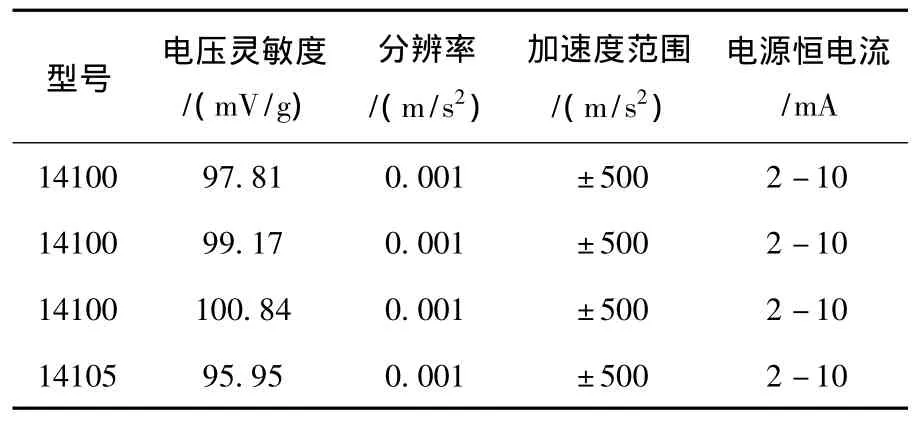
表2 传感器参数表Table 2 Parameter list of the acceleration sensors

3 电机振动频谱分析

电机振动频谱特征分析对电机振动抑制算法的设计是十分必要的，振动频谱特征可以为电机振动抑制算法及相关参数的确定提供参考。电机垂向或水平向振动信号实际都是多振动源在其方向上的叠加信号。因此，选择某一方向的振动信号频谱幅值情况来检验电机振动抑制算法性能不失一般性。故本节只讨论电机垂向振动频谱幅值情况。

3.1 电机振动频谱对比分析

因为用有效值来描述振动信号的能量，具有稳定性和重复性好的特点，故对所采集的振动加速度数据所绘制的基于FFT的频谱图，其幅度采用均方根值，即有效值，其单位为mg。图2给出了在调压器调压和变频器变频调速情况下不同转速所对应的频谱图。图2(a)表明，用调压器调压时，在50 Hz附近出现振动峰值，该振动峰值主要由工频引起，转速对此振动峰值频率略有影响;部分振动峰值比较明显地集中在200～410 Hz频带内，且振动峰值频率随速度的增加而增大;另外，在830 Hz附近又出现明显的振动峰值。用变频器变频控制时，从图2(b)的频谱形态可看出，在850 Hz以下，其频谱特征与调压器调压控制时的频谱特征类似，主要差别表现在振动峰值明显增大;在1 900 Hz以后振动幅度随转速提高更加明显，并在3 500 Hz附近出现振动峰值，且峰值频率随转速增加有所降低。由于电机振动频谱使用的是电机振动加速度数据，故其频谱幅值会随转速提高而增大。

图2 不同转速下的FFT频谱图Fig.2 FFT spectrums with different speeds

对于旋转系统，其振动信号中某些离散频率分量与主旋转频率有关。为了考察电机振动在0～200 Hz频带范围内频率分量随转速变化的情况，绘制了转速谱阵图。转速谱阵图是一个三维图，他将不同转速下的频谱特性绘制在同一个坐标系下，其3个轴分别表示频率、转速和振幅。图3是根据图2所对应的0～200 Hz频带内的数据绘制出来的转速谱阵图。从转速谱阵图中，可以分辨出系统的强迫振动与自由振动。与转速有关的强迫振动，其频率成分出现在原点(转速与频率为零)处引出的射线上，而与转速无关的自由振动部分则出现在固定的频率处［12］。因此，由图3(a)中所做的射线可清晰看出，电机采用调压器调压控制时，不同转速下的强迫振动情况，其强迫振动的频率即为一阶转频，且强度随转速的增加而增大;与图2(a)相比，图3(a)中50 Hz附近的最大振动峰值特征表现的更加清晰;图3(a)还十分清楚地反映了调压器调压调速时，电机在100 Hz处有振幅不大的自由振动，该自由振动频率为电网频率的2倍，故这个振动也可能是由定子异常引起的电磁振动，也可能是调压器调压调速电机系统的固有频率［12］，这可以通过电机的机械振动频谱分析来判断。

图3 0～200 Hz转速谱阵图Fig.3 Speed spectrum between 0～200 Hz

图4 0～800 Hz变频器驱动转速谱阵图Fig.4 0～800 Hz speed spectrum with inverter drived

而对于变频器变频调速的情况，由前节分析可知，在转子中的时间谐波电流与空间磁场作用，产生振动谐波转矩，从而引起转速的波动及电机振动，同时也使得电机振动的频率特征变得十分复杂，从图3(b)也充分说明了这一点。将图3(b)与图3(a)相比，由于变频器谐波影响，使得由一阶转频引起的强迫振动部分变得不十分明显，同时100 Hz的自由振动消失，出现在150 Hz频率处，且有些变形。为了更清楚地考察低频振动特征，图4给出了变频器驱动情况下0～800 Hz频带内的转速谱阵图。由该图可看出，在150 Hz、250 Hz和350 Hz附近出现不是很典型的自由振动分量，这说明变频器驱动的电机系统，其最低自由振动频率提高了，且由于谐波影响，激发出了更多的自由振动分量。这些都是由于变频器驱动时，各次电流时间谐波与电磁空间谐波相互作用所产生的各种附加谐波转矩或电磁激振力使得电机的振动频谱变得更加复杂。

3.2 变频器载波频率对电机振动的影响

变频器输出电流谐波情况受载波频率及载波比等因素的影响，为了获得比较平滑的正弦波形，往往希望载波频率尽可能高些，而载波频率受大功率逆变元件的开关频率限制，目前多采用IGBT三相桥式逆变器，其最高载波频率可达15 kHz。所采用变频器载波频率可通过参数 Pr.71方便地设置为3 kHz、6 kHz、9 kHz、12 kHz 和 15 kHz。

由逆变原理可知，逆变回路是由IGBT通过正弦脉宽调制SPWM后，产生呈正弦波的电流波形，而载波频率的大小、直接影响电流波形的质量及干扰程度，且载波频率的高低对变频器输出二次电流的波形是较为敏感和直接的［3］。当载波频率增高时，一个周期内脉冲的个数就增多，从而使得电流波形的平滑性变好，即电流波形更接近正弦。这样谐波就小，由此产生的振动谐波转矩也小。然而，载波频率增高同样也会带来一些诸如变频器自身损耗增大、IGBT温度上升等不利影响。而当载波频率降低时，电流波形正弦性变差，使电机气隙的高次谐波磁通增加，引起振动谐波转矩加大，电机可能发生周期性转速变动，并使噪声变大。图5给出了在最低载波频率3 kHz下和最高载波频率15 kHz下电机垂向振动的频谱图。从图中可明显看出，随着载波频率的增加，电机垂向振动幅度将显著降低，且高频段的振动峰值频率随载波频率的增加而增大。从图5(a)和图5(b)可看出，载频设置为3 kHz时，其振动峰值频率小于3 kHz，当载波频率提高到15 kHz时，其振动峰值频率增加到3.5 kHz附近;同时还可看出，在设定载波频率固定的情况下，其振动峰值频率随着转速的提高而下降，这个现象是由变频器采用分段同步调制方式引起的。

图5 不同载波频率下电机振动频谱比较Fig.5 Comparison of the motor vibration spectrums with different carrier frequencies

式(3)、式(4)和式(7)只给出了各次谐波峰值与调制系数m成正比的关系，而与载波频率之间的关系描述并不明显。关于谐波分量与载波频率的关系，文献［13］利用贝塞尔函数项级数，对其进行了具体分析，推导得出谐波分量的频率为

对应的振幅为

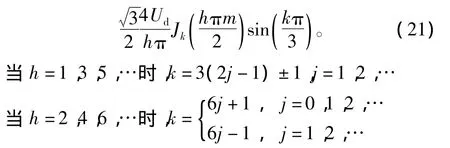
式中:ωs为载波频率;Jk为k阶贝塞尔函数。

从式(20)和式(21)可知，谐波中无载波频率ωs的整数倍谐波，无调制波频率ω1的3的整数倍谐波。

4 结语

通过异步电机振动谐波理论及振动频谱特征分析可知，当采用变频器驱动异步电机时，与调压器调压相比，电机的振动频谱特征在850 Hz以下其基本形态类似。但通过进一步频率细化，可发现其一阶转频引起的强迫振动在转速谱阵图中表现出波形畸变，而自由振动波形也变得不够典型，并激发出了更多的自由振动分量。由于变频器的引入，电机垂直方向的振动峰值明显增大，且振动峰值出现的频带由调压器调压调速时的850 Hz扩展到接近4 000 Hz。另外，随着变频器载波频率的增加，电机垂向振动幅度将显著降低，且高频段的振动峰值频率随载波频率的提高而增大。这些结果表明，变频器驱动异步电机时，由于高阶振动谐波转矩等因素，使得电机的振动特征更加复杂。本文的振动频谱特征分析，为今后电机振动抑制算法的设计及算法评价提供了一个基础。

［1］ 程宝平.SPWM的谐波及抑制［J］.电气技术，2010(6):47－49.

CHENG Baoping.Harmonic analysis and harmonic suppression of SPWM［J］.Electrical Engineering，2010(6):47 －49.

［2］ 徐顺刚，许建平，曹太强.SPWM逆变电源输出谐波分析及抑制方法研究［J］.电子科技大学学报，2010，39(5):701－705.

XU Shungang，XU Jianping，CAO Taiqiang.Analysis and research of SPWM inverter harmonic suppression［J］.Journal of U-niversity of Electronic Science and Technology of China，2010，39(5):701－705.

［3］ 周京华，吴理心，章小卫，等.多电平逆变器多载波调制策略的谐波分析［J］.电机与控制学报，2011，15(5):63－71.

ZHOU Jinghua，WU Lixin，ZHANG Xiaowei，et al.Harmonic analysis of multi-level inverter multi-carrier modulation strategy［J］.Electric Machines and Control，2011，15(5):63 －71.

［4］ 朱世林.异步电动机谐波转矩分析［J］.江西工业大学学报，1988，10(4):34－43.

ZHU Shilin.The analysis of the harmonic torque of the asynchronous motor［J］.Journal of Jiangxi Polytechnic University，1988，10(4):34－43.

［5］ 张晟，余海涛，陈小林.SPWM型逆变器驱动感应电机电压谐波分析和脉动转矩仿真［J］.自动化与仪器仪表，2008(4):83－84.

ZHANG Sheng，YU Haitao，CHEN Xiaolin.Voltage harmonic analysis and pulsating torque simulation of induction motor drived by SPWM inverter［J］.Automation ＆ Instrumentation，2008(4):83－84.

［6］ 藏英杰.变频调速系统的三相鼠笼异步电动机［J］.机车电传动，1980(2):29－35.

ZANG Yingjie.Three phase squirrel cage induction motors of frequency control system［J］.Electric Drive for Locomotives，1980(2):29－35.

［7］ 杨琰，窦满峰.VVVF变频器驱动高功率密度异步电机的电源谐波研究［J］.电机与控制学报，2006，10(1):49－51.

YANG Yan，DOU Manfeng.Research on supply harmonic of high power density induction motor equipped with VVVF converter［J］.Electric Machines and Control，2006，10(1):49 －51.

［8］ TSE K K，CHUNG H S，HUI S Y R，et al.Analysis and spectral characteristics of a spread-spectrum technique for conducted EMI suppression［J］.IEEE Trans on Power Electronics，2000，15(2):399－410.

［9］ 杨顺昌，廖勇，余渝.考虑谐波影响后交流励磁电动机的电磁转矩的分析与计算［J］.电工技术学报，2003，18(1):5－9.

YANG Shunchang，LIAO Yong，YU Yu.Analysis and calcualation of electromagnetic torques for AC excited motors incorporating the effect of harmonic currents in the excitation source［J］.Transactions of China Electrotechnical Society，2003，18(1):5－9.

［10］ 藏英杰.变频调速系统的三相鼠笼异步电动机(续)［J］.机车电传动，1980，(5):31－35.

ZHANG Yingjie.Three-phase squirrel cage induction motor of variable frequency speed regulating system(continued)［J］.E-lectric Drive for Locomotives，1980(5):31 －35.

［11］ 李伟，韩力.逆变器供电的感应电动机谐波转矩分析与计算［J］.微特电机，2005(4):6－9.

LI Wei，HAN Li.Analysis and calculation of harmonic torques for induction motor fed inverter［J］.Small＆ Special Electrical Machines，2005(4):6 －9.

［12］ 樊新海.工程测试技术基础［M］.北京:国防工业出版社，2007:84－88.

［13］ 曹立威，吴胜华，张承胜，等.SPWM谐波分析的一般方法［J］.电力电子技术.2002，36(4):62－65.

CAO Liwei，WU Shenghua，ZHENG Chengsheng，et al.A general method of APWM harmonic analysis［J］.Power Electronics，2002，36(4):62－65.

(编辑:于智龙)

Analysis of vibration spectrum characteristics for asynchronous motor driven by inverter

LI Wen， ZHAO Hui-min， DENG Wu
(Software Institute，Dalian Jiaotong University，Dalian 116028，China)

In order to propose a kind of more effective algorithm for motor vibration suppression，the spectrum characteristic was discussed.The vibration data sampling unit of asynchronous motor drive system and the motor vibration data sampling under different running conditions were introduced.Vibration spectrums and speed spectrums of different speeds were given under two control manners by using inverter and voltage regulator.Motor vibration characteristic and influence of inverter carrier frequency on the vibration characteristic were compared and analyzed by means of those spectrums.Comparison and analysis show that the one-order rotation frequency causes the forced vibration and the free vibration wave occurs the distortion，and the vibration peak value increases，when asynchronous motor is driven by the inverter.The motor vibration magnitude decreased obviously when the inverter carrier frequency increases.High-order harmonic torque is introduced into the inverter to make more complex vibration characteristic of asynchronous motor.The spectrum characteristics analysis of motor vibration provides the basis of design and appraisal for motor vibration suppression algorithm.

asynchronous motors;inverter;vibration spectrum;harmonic analysis

TM 301.4

A

1007－449X(2012)08－0067－07

2011－03－11

国家自然科学基金(60870009);国家"863"计划项目资助(2012AA040912);牵引动力国家重点实验室开放课题资助(TPL1203)

李 文(1960—)，女，博士，教授，研究方向为智能控制、信号处理;

赵慧敏(1977—)，女，博士研究生，副教授，研究方向为智能控制、信号处理;

邓 武(1976—)，男，博士研究生，副教授，研究方向为智能技术。

李 文