蛇摆的研究与制作
2012-02-01薄春卫孔祥明贾肖婵吴建海段雪松
薄春卫,孔祥明,贾肖婵,吴建海,段雪松
(1.天津开发区职业技术学院,天津300130;2.河北工业大学,天津300401)
1 蛇 摆
蛇摆,原意为pendulum waves,即摆波[1-2].蛇摆由多个排成一列的摆长渐变的单摆组成,由于每个单摆的周期不同,而相邻单摆间的频率差相等,所以当它们同时摆动后,在空间中的排列将呈现周期性的变化.
蛇摆运行如图1所示,图1(e)摆长最长的摆球大概摆动15次,图1(h)摆长最长的摆球大概摆动30次.

图1 蛇摆的实验现象(相邻单摆的频率差为0.03Hz)
2 蛇摆的原理
2.1 摆长方程
假设蛇摆有n+1个摆球,所有摆球回到初始波形为1个周期Γ,此时最长的单摆恰好摆动N次,次长的单摆恰好摆动N+1次,最短的单摆摆动N+n次,单摆的周期则为每两个单摆的间隔为d,因此距离为x=nd,由单摆公式


可得摆长方程

其中:T为单摆周期,L为摆长,g为重力加速度.从式中可看出不同位置的单摆摆长不同.
2.2 蛇摆函数
蛇摆在运动时为正弦函数,故可设位移为y(x,t)=Acos(ωt+φ),因为φ为起始位置,可设为零,以利于计算,单摆摆长的不同,ω会随位置而改变,可写成ω(x),角频率由(1)和(2)式推得为,只考虑ω的影响,则位移为

将(3)式整理可得

2.3 蛇摆的周期性
蛇摆摆动后经过数个周期(mΓ)仍和第一周期是相同的:

所以y(x,t+mΓ)=y(x,t).由此推得了蛇摆的周期性[3].
3 蛇摆的制作
3.1 尺寸设计
蛇摆的尺寸设计见表1,有如下特点:
a)摆球越多,蛇摆形成的曲线越细腻、丰富,制作难度也随之增加;较少的摆球制作难度低,表现力也相应变差。10~15个球是较为合适.
b)1号球摆长32cm是根据手边材料尺寸就近选择的,如果选择更大尺寸,对降低调节难度是有帮助的.最大摆长确定后,依据频率差依次计算出相邻摆球的周期和摆长.
c)计算使用的g要取当地的准确值,调好后如换到其他纬度地区使用,最好重新调节,效果更好;本实验中所用g天津=9.801 1m/s2.
d)频率差Δf宜选择0.03Hz和0.04Hz左右.较大的Δf使调节变得容易,但图形变化快不容易观察现象;较小的Δf可获得缓慢而细腻的变化,但精度要求更高,所以调节起来较困难.
e)用双线摆代替单摆实现一维摆动,以便观察.摆球和摆线之间采用活动连接,2个悬点,1个固定,1个与微调机构连接.
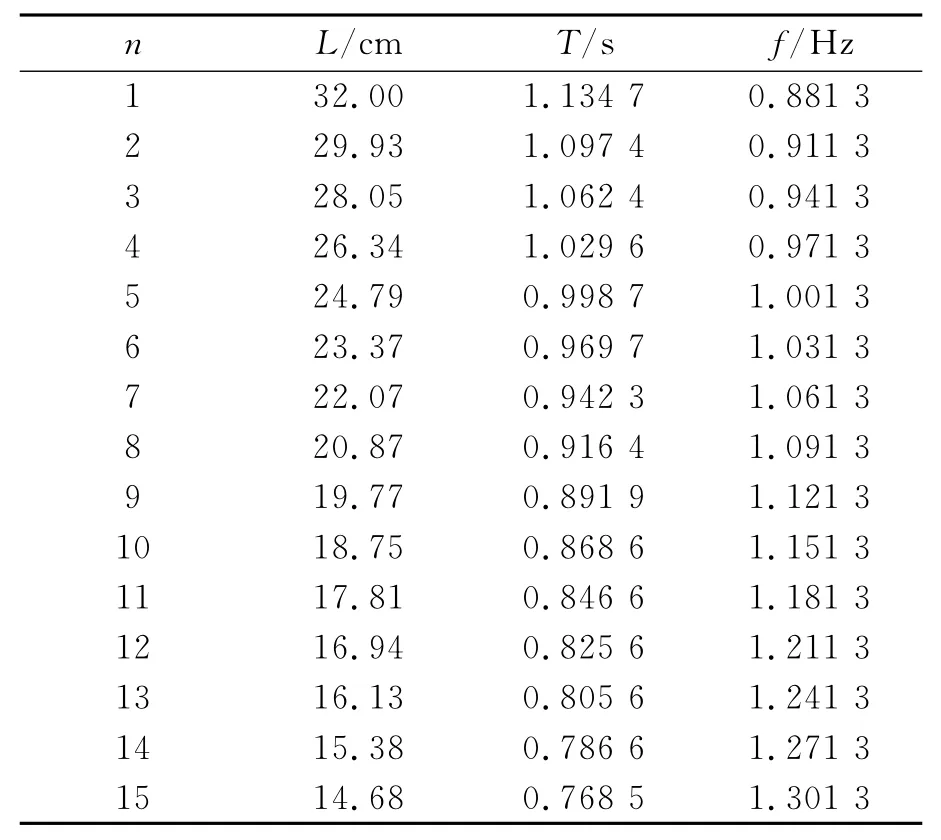
表1 蛇摆的尺寸设计
3.2 选 材
1)摆球宜选择密度较大的钢(铁)球或铅球,这样可以忽略空气阻力产生的影响,本实验采用直径25mm的镀铬铁球.
2)摆线应保证结实程并且尽可能细,使观众注意力集中在摆球组成的图案上,笔者选用3种线进行比较,优缺点如下:a.棉线,不能同时满足演示效果和结实程度的要求,有捻,调节时易自我缠绕;b.尼龙渔线,0.23mm,透明,保证演示效果和结实程度要求,调节时有轻微自缠绕,有记忆,在拐点处有一定弯折,长期存放有少许伸长,需重新调节,c.大力马渔线,材料PE,直径0.2mm,保证演示效果和结实程度,无自我缠绕,无记忆效应,适合微调,长期存放无伸长,效果最好.
3)调节机构可选用乐器(如吉他、提琴)弦钮.
3.3 制 作
图2[4]~5是蛇摆的不同造型,其中图2~3[5]为I型蛇摆,这种蛇摆的悬点连线为曲线,摆球连线为直线;图4为Ⅱ型蛇摆,图5为Ⅱ型蛇摆的具体结构,笔者制作的蛇摆也属于Ⅱ型,这种蛇摆的悬点连线为直线,摆球连线为曲线.相比较而言,I型蛇摆的摆球连成一线,现象更美观,甚至可以省掉调节旋钮.但弯曲悬梁的制作比较困难,稍有不慎,连修改的机会都没有,只能重做.而Ⅱ型的制作难度相对较低.

图2 美国亚利桑那州立大学的蛇摆

图3 旧金山中央美术宫探索馆中的蛇摆

图4 美国马里兰大学的蛇摆

图5 Ⅱ型蛇摆的结构
3.4 调 节
先用米尺粗调摆长(精确到mm),再用分度值为0.01s的秒表测量100个单摆周期进行细调,可使周期精确到ms.由于有乐器弦钮的帮助,调节并不困难.如果有配合光电门的数字毫秒计,则调节更加容易.
4 制作心得
1)蛇摆不仅向人们说明了单摆的周期性,还展示了等频率差的累积效果所幻化成的不断变换的美妙图案.
2)由于每个单摆的周期不能恰好调到相应的大小,总会有误差存在,又由于完成1个蛇摆周期,每个单摆要完成十几个甚至几十个单摆周期,所以即使误差很小,此时也会被放大十几倍甚至几十倍,从而影响图案的美观.
3)摆长的精细调节关系到蛇摆制作的成败.因此I型蛇摆横梁的制作要十分精准,而Ⅱ型蛇摆由于有乐器旋钮这样的蜗杆机构辅助,制作和调节则相对容易.
笔者在此基础上制作了夜光蛇摆(图6),可消除背景对观察实验的影响.

图6 夜光蛇摆
[1] Berg R E.Pendulum waves:A demonstration of wave motion using pendula[J].Am.J.Phys.,1991,59(2):186-187.
[2] Flaten J A,Parendo K A.Pendulum waves:A lesson in aliasing[J].Am.J.Phys.,2001,69(7):778-782.
[3] 中央大學物理實驗演示(蛇擺)[EB/OL].http://demo.phy.tw/experiment/dynamics/pendulumwave/
[4] PIRT Unveils New Pendulum Wave Display[EB/OL].http://pirt.asu.edu/news/2004-04-12/pirtunveils-new-pendulum-wave-display.
[5] University of Maryland Physics Lecture-Demonstration Facility[EB/OL].http://www.physics.umd.edu/lecdem/services/demos/demosg1/g1-82.htm.
