利用平面平晶反射干涉制作低频全息光栅

2012-02-01黄婉华程敏熙陈映纯

物理实验 2012年4期

黄婉华，程敏熙，陈映纯

（华南师范大学物理与电信工程学院，广东广州510006）

1 引言

全息光栅是常用的光学元件，在光学信息处理技术中有着广泛应用[1]，如用于图像加减[2]、微分及分光等[3].制作全息光栅的常用方法主要有：马赫－曾德尔干涉[4]、阿贝成像法[5]、菲涅尔双面镜干涉法等[6]，这些方法各有优缺点，有的光路比较复杂且调节麻烦，有的需要现成的标准光栅.本文根据杨氏干涉原理，利用平面平晶反射形成平行干涉条纹，制作全息光栅.光路简单，元件少，调节方便，干涉条纹清晰稳定.制作的光栅可在空间滤波[7]、图像相加减及光学微分等教学实验中应用.

2 干涉条纹形成原理分析

2.1 杨氏干涉原理

杨氏干涉原理如图1所示.图1中S为点光源，照明2个相距为d的小孔S′和S″，假设波长为λ，小孔到接收屏的距离为D.若满足d≪D，则在远处屏上出现等距的平行干涉条纹，其条纹间距为[8]

因此，若光栅面积不太大，利用杨氏干涉条纹，可以制作全息光栅.

2.2 利用平面平晶获得杨氏干涉条纹的分析

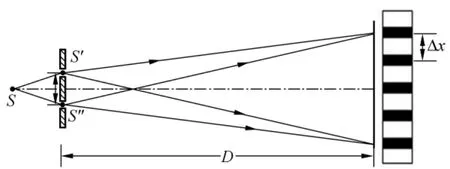
图1 杨氏干涉原理图

图2 利用平面平晶获得杨氏干涉条纹光路图

在图2中，激光通过小扩束镜和针孔组成的空间滤波器及凸透镜后可形成大孔径的平行光、发散光或会聚光，再照明平面平晶，经2个表面反射后可形成杨氏干涉条纹.如果扩束镜位于凸透镜1倍焦距内，从其出射的是发散光或球面光波.

以照明平面平晶的光为发散光为例，说明形成杨氏干涉条纹的过程.如图3所示，发散光可以看成是点源S射出来的球面光波，经平面平晶2个面反射后，在其另一侧出现2个虚点源（镜面像）.2个点源发射的2束光在远处相遇出现干涉条纹.

设O1S′为平面平晶第一个平面到像点S′的距离，O2S″为平面平晶第二个平面到像点S″的距离，设平面平晶与光轴的夹角为θ，光束Ⅱ在第一个平面的入射点为C，光线Ⅱ经第二个平面反射后由第一个平面出射点为E，θ1为折射角，n为空气的折射率，n1为平面平晶的折射率，h为SC的距离，设平面平晶的厚度为D0.根据几何光学有[3]

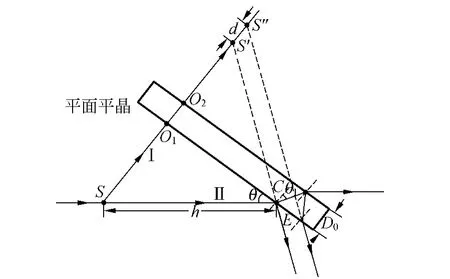
图3 平面平晶形成杨氏干涉条纹原理图

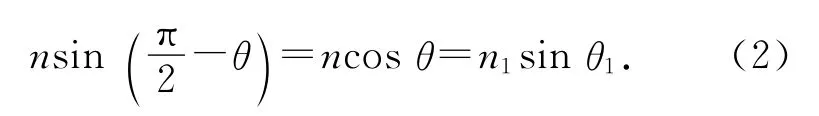
由图3中几何关系，在Rt△SO1C中，

又由于

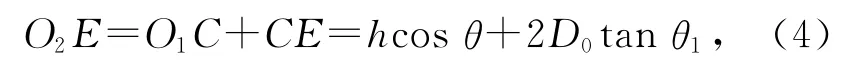
由（2）式～（4）式可得两等效光源的间距为

即两等效点光源的间距与平面平晶的厚度D0、平面平晶与光轴的夹角θ有关，与h无关.可见，通过调节θ，可以改变点光源的间距，从而得到所需光栅常量的光栅.由（1）式及（5）式可求条纹间距

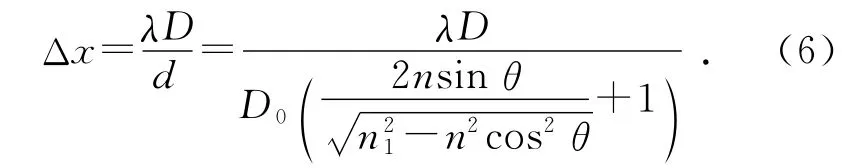
图4是条纹间距与平面平晶与光轴夹角的关系.可见，当平面平晶与光轴的夹角θ增大时，在干板处所形成的杨氏干涉条纹间距减小，当夹角θ减小时，杨氏干涉条纹的间距反而增大.因此，可以通过调节平面平晶与光轴的夹角，实现对条纹疏密的控制.如当D0＝15mm，λ＝632.8nm，θ＝45°，n1＝1.51，D＝25cm，d＝11.7mm，Δx＝4.52×10－3mm.而实际上，改变点光源S的发散角，在一定程度上也可以调节条纹间距.

图4 杨氏干涉条纹间距Δx与平面平晶和光轴夹角θ的关系曲线

另外，设入射平面平晶的光强为I0，对于该规格的平面平晶（材质为玻璃），其对632.8nm波长反射率约为5%，由第一个平面反射光束光强为5%I0，而经第一面透射及第二面反射后的光束光强为95%×5%×95%×I0＝0.045I0，2束光形成的干涉条纹衬比度[8]为

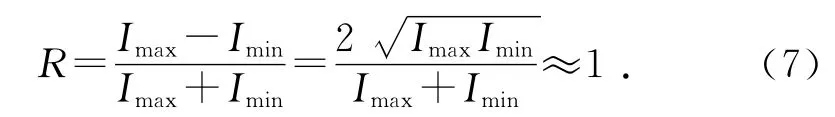
因此，在一定区域范围内，平面平晶反射形成的干涉对比度比较高，适合于低频全息光栅的制作[8].

3 实验及过程

3.1 实验光路

图5为拍摄全息光栅的光路，空间滤波器系统由扩束镜和针孔组成，平面平晶厚度为15mm.

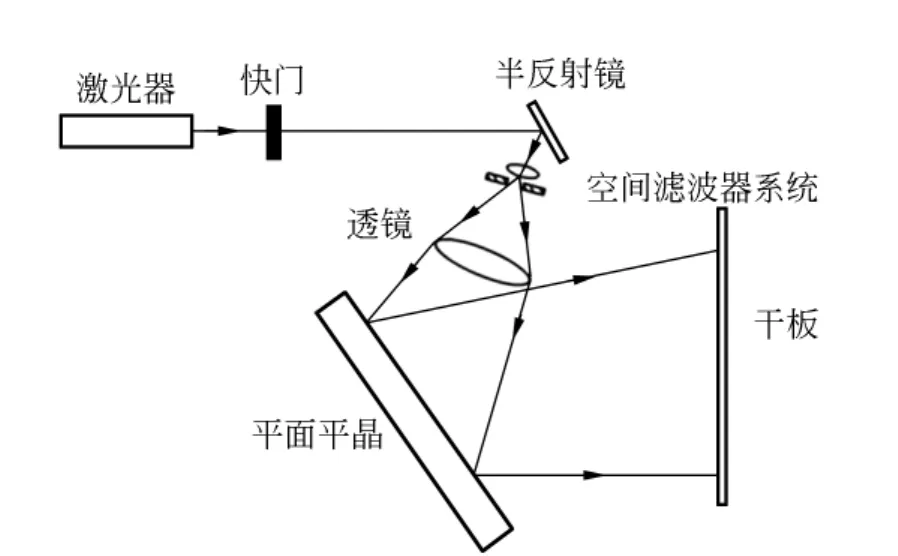
图5 实验光路示意图

3.2 实验光路的调节及条纹间距的测量

按照图5所示摆放各种光学元件，点亮激光器，使激光器发出的光经快门及反射镜反射后改变传播方向，经空间滤波器后成为高质量的均匀球面光束，调节凸透镜与空间滤波器之间的距离，使得这束均匀光经过凸透镜之后成为发散的光束（也可以形成会聚或者平行光，这里以发散光为例），照射平面平晶，经其反射后在干板处形成干涉条纹.以拍摄空间频率为20mm－1的低频全息光栅为例，在干涉条纹处放置移测显微镜对准条纹，通过移测显微镜测量条纹间距.在平面平晶的厚度一定的情况下，通过调节平面平晶与水平线的夹角θ，使条纹间距为0.05mm，即可制得所需的光栅[9].另外，也可以在干涉条纹处放置已知焦距的凸透镜，测量由2束光在其焦平面的2个光点的距离，通过计算得到条纹间距.

不同的全息干板，其处理工艺也不相同.对于重铬酸盐明胶全息干板，将干板置于干涉场中曝光70s，再经过在蒸馏水中静置以及在不同浓度的异丙醇中脱水再取出吹干，最后用干净的玻璃片封装[10].