超临界平面耦合轴向运动梁的静平衡分岔
2012-01-31黄慧春陈立群
黄慧春, 丁 虎, 陈立群,3
(1.上海第二工业大学机电工程学院,上海201209;2.上海大学上海市应用数学和力学研究所,上海200072; 3.上海大学理学院,上海200444)
动力传送带、空中缆车索道、高楼升降机缆绳等工程元件,均可模型化为轴向运动梁,其物理模型如图1所示.作为典型的陀螺连续系统,由于陀螺项的存在,使得针对轴向运动梁振动的分析广受关注[1-5].考虑几何非线性,轴向运动梁的振动通常遵循横向与径向(轴向)相耦合的平面运动规律.Thurman等[6]首先提出了轴向运动梁平面耦合运动的控制方程.Tabarrok等[7]推导出了另外一种耦合平面的控制方程,而且基于静态梁的特征函数对控制方程进行了离散.Riedel等[8]在Galerkin截断的基础上,运用多尺度方法研究了轴向运动梁横向与径向耦合的非线性受迫振动.沈建和等[4]通过增量谐波平衡法研究了横向与径向耦合的平面受迫振动响应.这些针对平面耦合控制方程的研究工作都具有一个共同特点,即通过某种途径将耦合方程简化,仅保留少量低阶非线性项.而文献[2,9]则直接利用数值方法研究了未加简化的亚临界轴向运动梁的平面耦合运动.
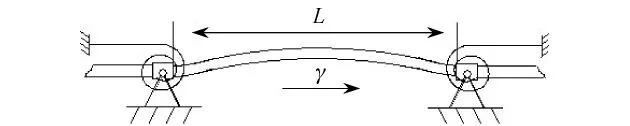
图1 轴向运动梁模型Fig.1 Model of axially moving beam
Wickert[10]基于“准静态假设”的弹性梁的自由振动模型,建立了超临界轴向运动的静平衡位形,以及对应于每个分岔解的连续陀螺系统的标准控制方程.Wickert的研究证明,对于超临界轴向运动梁,因非线性引起的非平凡静平衡位形是一切研究工作的前提.但是,对于轴向运动梁两端固定边界条件下,有关超临界轴向运动梁的静平衡分岔研究,以及对应于分岔解的连续陀螺系统的标准控制方程的建模工作还未见有报道.
针对以上问题,本研究通过发展有限差分方法,直接数值研究两端固定边界条件下,超临界轴向运动弹性梁的平面耦合运动的静平衡分岔问题.
1 平面耦合模型
假设截面积为A、密度为ρ、初始张力为P的梁以一致的速度γ(常数)沿轴向运动,梁弹性模量为E,这里只考虑梁横向和径向变形.在径向空间坐标x处,t时刻横向位移为v(x,t),轴向位移为u(x,t).对于细长的梁(例如,满足I/(Al2)<0.001),耦合动力学方程的无量纲形式为[1-2]
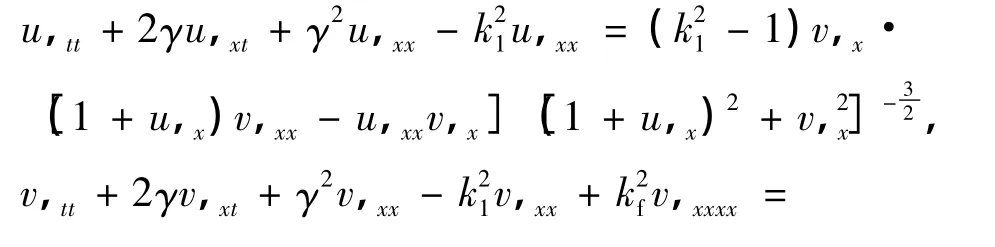
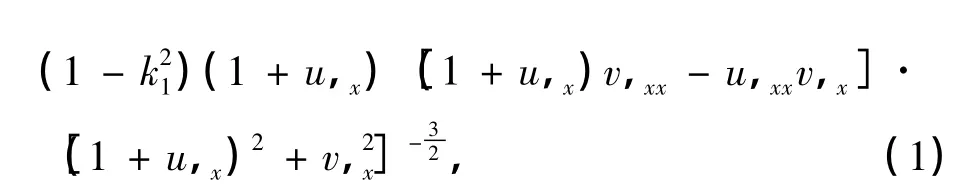
式中,“,x”和“,t”分别表示对x和t的偏微分.相应的无量纲化变量和参数分别为
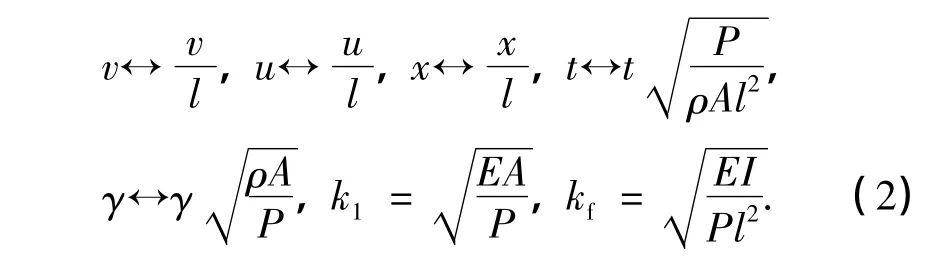
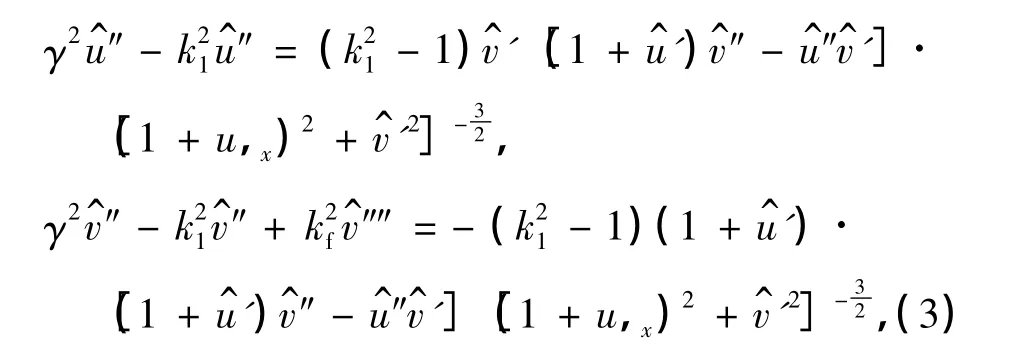
式中,“'”表示对x取导数,“^”表示静平衡位移.
2 计算方法
这里仅考虑梁的两端由带有扭转弹簧的光滑套筒固定的边界条件[2]:
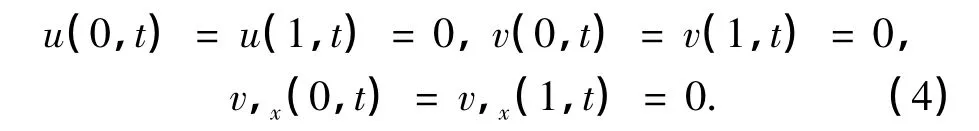
静平衡位形可以通过下述两种方法计算得到.
2.1 静态方程迭代
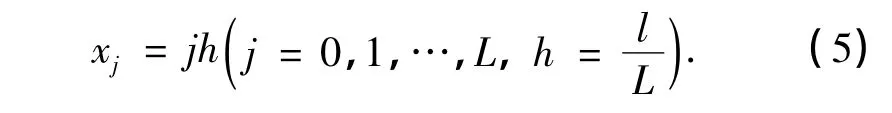
以uj和vj表示函数u(x)和v(x)在网格xj处的值.应用中心差分法离散空间导数[4],得
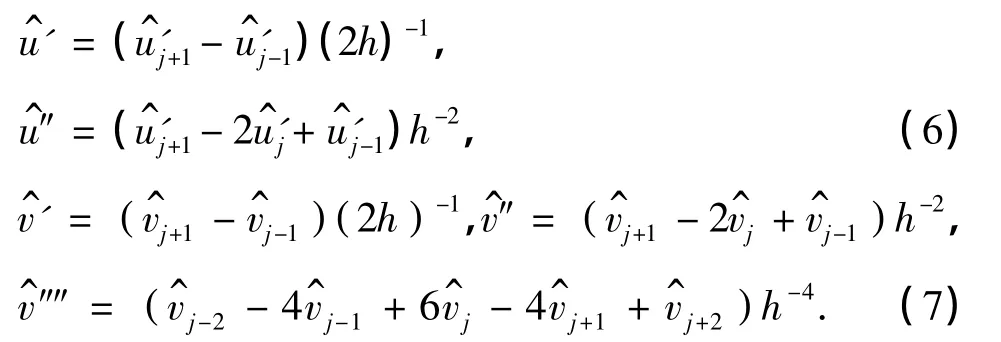
此时,相应的两端固定的边界转变为
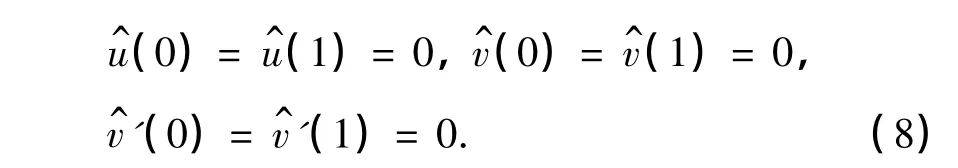
将方程(6)和(7)代入方程(3),可以得到关于uj和vj的一系列代数方程.通过迭代方法求解,可得
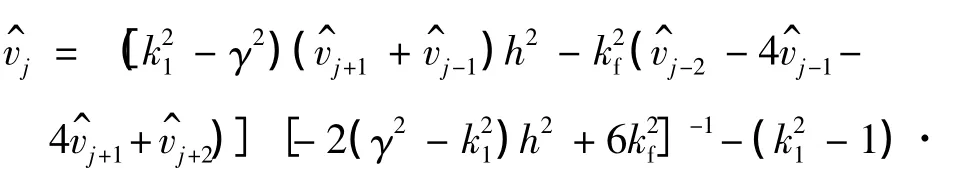
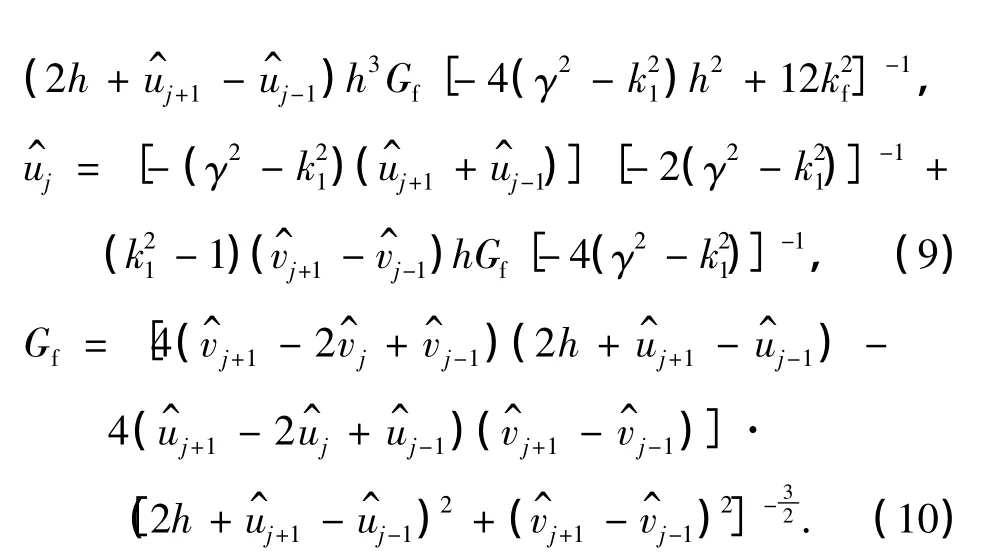
给定初始条件及参数的数值,可解得离散点uj和vj的值作为方程(3)中连续解u(x)和v(x)的近似解.
2.2 黏弹性模型的非平凡分岔解
考虑Kelvin模型的黏弹性材料梁,则耦合黏弹性轴向运动梁的动力学方程的无量纲形式为[1-2]
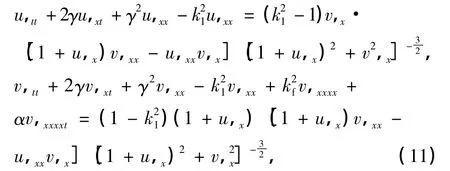
式中,无量纲参数
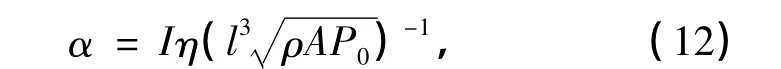
其中η为黏性系数.引入步长为τ的均匀节点,
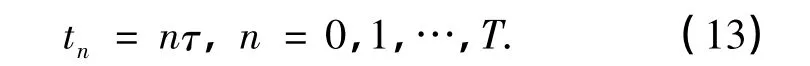
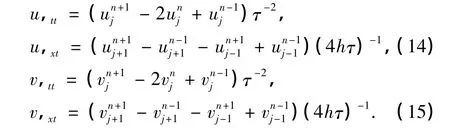
应用有限差分法数值求解方程(11)需要式(4)和(5)以及相应的初始条件,因此,引入如下初始条件:
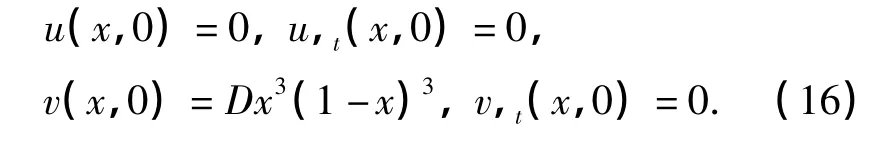
3 数值计算结果
在数值仿真中,取 τ=10-5,h=10-2(即L= 100),D=0.01.以铜材料为例[2],其弹性模量E= 1.08×1011Pa,密度ρ=8 450 kg/m3.取初始张力P=4 225 N,轴向速度 γ=150 m/s,宽度 W= 0.04 m,高度H=0.02 m的矩形横截面积梁,无量纲黏性系数α=0.000 1.
在空间离散式(5)和时间离散式(13)的基础上,结合初始条件以及梁两端固定的边界条件,通过差分法计算方程(11)的横向和径向的时间响应历程,结果如图2所示,图中横纵坐标均为无量纲量.图2表明非平凡分岔解能够通过黏性方程计算得到,而且梁横向运动的幅度要远大于径向运动幅度.数值计算结果显示,梁的振动幅度随时间衰减,而且在经历足够长的时间之后,梁的形状趋向于静态非平凡平衡位形.因此,超临界轴向运动梁的非平凡静平衡位形可以通过这种途径得到.
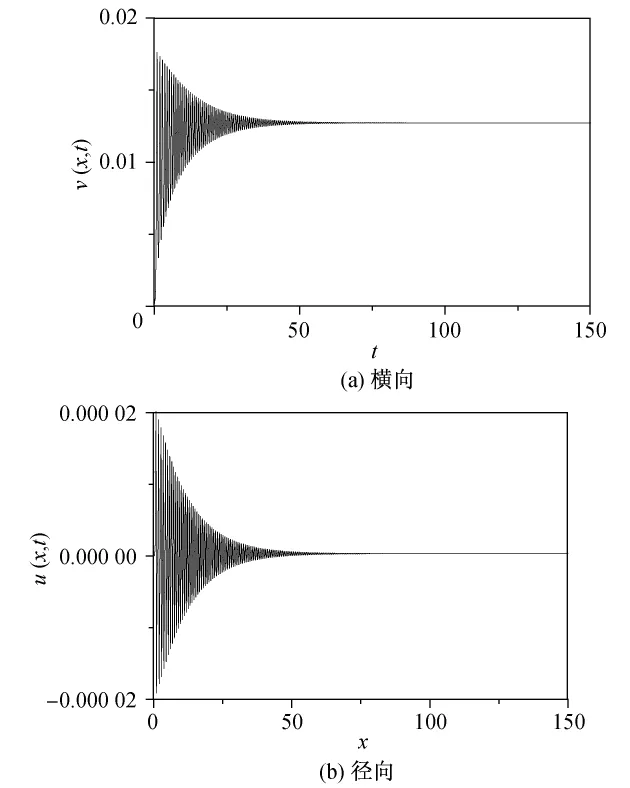
图2 耦合运动的时间响应历程Fig.2 Time history for coupled motion
通过式(9)和方程(11)计算得到的超临界轴向运动梁横向与径向耦合的平面非平凡分岔解的定性比较如图3所示,其中的点表示通过迭代格式(9)计算得到的结果,实线表示通过黏弹性自由振动方程(11)衰减得到的结果.各参数取值分别为初始张力P=4 225 N,轴向速度γ=150 m/s,宽度W=0.04 m,高度H=0.02 m,无量纲黏性系数α=0.000 1.观察发现,通过2种途径得到的计算结果完全吻合.
图4比较了初始张力和横截面积对超临界轴向运动梁中点静平衡位移的影响.由图可以发现,当轴向运动梁的轴向速度达到一定值时,轴向运动梁会发生静平衡分岔.图4(a)表明了初始张力的影响,其中梁的宽度W=0.04 m,高度H=0.02 m,点、实线和虚线分别表示初始张力P=2 112.5,4 225.0和8 450.0 N时的情形.由图可以发现,随着初始张力的增大,临界分岔速度逐渐减小.图4(b)表明了梁的横截面积的影响,其中初始张力P=4 225 N,梁宽度W=0.04 m,点、实线和虚线分别表示高度H= 0.010,0.015和0.020 m时的情形.由图可以发现,梁的横截面积变大将导致临界分岔速度变大.
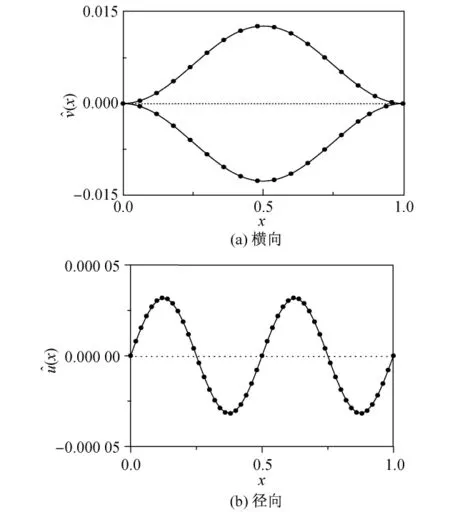
图3 2种方法计算非平凡非静平衡解的比较Fig.3 Comparison of the non-trivial equilibrium solutions between two methods
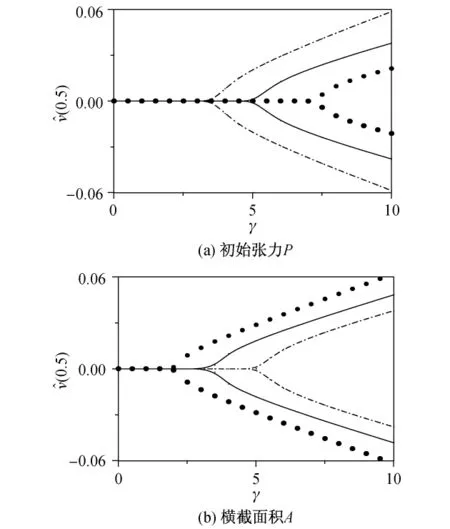
图4 系统参数对随速度变化的横向静平衡分岔的影响Fig.4 Effectsofparameterson thebifurcation diagram with the axial speed
4 结束语
本研究讨论了超临界轴向运动梁横向与径向耦合平面非平凡静平衡位形分岔问题.在梁两端固定边界条件下,以铜材料梁为例,结合有限差分法,分别通过2种方法(迭代格式(9)和黏弹性自由振动方程(11))研究耦合平面的非平凡分岔解.数值计算结果表明,在超临界范围内,横向与径向相耦合的平面内出现了非平凡的平衡解,而且2种方法得到的超临界速度下非平凡分岔解是完全吻合的.进一步对梁中点位置的静平衡分岔进行比较发现,非平凡平衡位形的最大位移随轴向速度的增大而增大,随初始张力及梁的横截面积的增大而减小;另一方面,随着初始张力的增大,临界分岔速度随之减小,而梁的横截面积的变大将导致临界分岔速度变大.
[1] CHENL Q,DINGH.Steady-state responses of axially accelerating viscoelastic beams:approximate analysis and numerical confirmation[J].Sci in China G,2008,51(11):1707-1721.
[2] DINGH,CHENL Q.On two transverse nonlinear models of axially moving beams[J].Sci in China E,2009,52(3):743-751.
[3] 冯志华,胡海岩.内共振条件下直线运动梁的动力稳定性[J].力学学报,2002,34:389-400.
[4] 沈建和,陈树辉.非线性振动系统极限环振幅与频率的控制[J].振动与冲击,2009,28(6):90-92.
[5] 高美娟,张伟,姚明辉,等.压电复合材料层合板的混沌动力学研究[J].振动与冲击,2009,28(6):82-85.
[6] THURMANA L,MOTEC D,Jr.Free,periodic,nonlinear oscillation of an axially moving strip[J].J Appl Mech,1969,36:83-91.
[7] TABARROKB,LEECHC M,KIMY I.On the dynamics of an axially moving beam[J].J Franklin Ins,1974,297:201-220.
[8] RIEDELC H,TANC A.Coupled,forced response of an axially moving strip with internal resonance[J].Int J Non-Linear Mech,2002,37:101-116.
[9] 丁虎,陈立群.轴向运动黏弹性梁平面耦合非线性受迫振动[J].上海大学学报:自然科学版,2009,15 (6):649-652.
[10] WICKERTJ A.Non-linear vibration of a traveling tensioned beam[J].Int J Non-Linear Mech,1992,27:503-517.
