基于本征正交分解方法的多段翼型流动分析
2012-01-31范晨麟李孝伟
范晨麟, 李孝伟
(上海大学上海市应用数学和力学研究所,上海200072)
飞机起飞和着陆时的稳定性和安全性问题已越来越受到人们的重视,所以,有关增升装置的研究一直都是飞机设计中的重要环节.多段翼型是增升装置的二维构型,研究其流动结构及气动性能对于提高增升装置的设计水平有着十分重要的意义.
流动结构的复杂特征使得对多段翼型进行实验研究和理论研究都有很大困难,所以,近年来数值模拟方法已成为研究多段翼型流动的首要手段.但是,在流动状态参量如迎角、马赫数等发生变化时,通过数值模拟将会得到海量的流场数据.如何从这些海量的数据中获得流动的主要信息,甚至从已知的信息出发去预测一些新的信息,已成为数值处理研究中的一个重要课题.
本征正交分解方法(POD),又称为Karhunen-Loeve展开,是新近发展起来的一种处理海量数据的有效手段[1].它提供了一种独特的描述随机场的方法,即将随机场写为基函数——本征模态的级数展开式,而这些本征模态取决于随机场本身.由于这些本征模态在均方意义上是统计最优的,因而,在展开式中只需要少量的项数即可较准确地描述随机场,因此它又被作为数值模型的一种有力的降解和简化工具.POD方法中的本征模态是按照对应本征值所含流场能量的大小进行排序的,因此,通过捕捉高能量本征模态能很好地描述和分析随机场的特性;同时,由于能够得到在状态参量变化的有效范围内的所有流场信息,因此,POD方法兼具一定的预测功能.基于此,POD方法被广泛地应用于流体力学的研究中[2].
在复杂外形的流场计算中,为了使计算网格的生成更简单,同时能保持高质量,一般都会采用多块分区网格技术,如本工作中的多段翼型流动计算就是采用多块嵌套网格技术.运用嵌套网格技术,意味着会存在“挖洞”建立内边界的过程,此时,会留下一些没有实际意义且不参与流场计算的“洞中点”.如果用POD方法来处理采用嵌套网格技术得到的数值结果,首先要面对的问题就是如何处理“洞中点”上携带的信息.如果对这些点都采用POD方法进行处理分析,则会在一定程度上影响流场的重构和模态分析的准确性,所以需要对这些点进行特殊处理.
本工作首先采用数值模拟技术对迎角变换过程中的多段翼型的流场进行计算.在网格的布局方面采用嵌套网格技术,在得到一系列的数值解以后,运用POD方法对计算数据进行后处理,以帮助理解流场的主要结构和信息.在处理“洞中点”时,主要运用预处理方法对无意义点进行筛选和剔除,避免这些点对整个POD后处理分析的干扰和影响.
1 控制方程
流动控制方程[3]为Navier-Stokes(N-S)方程:
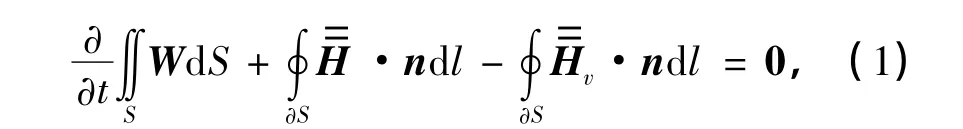
式中,
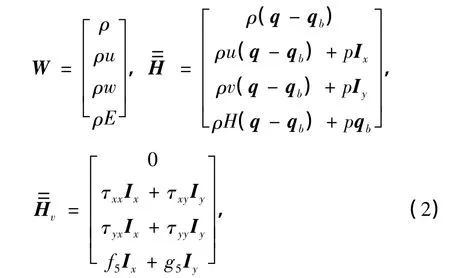
式中,ρ,(u,v),E,H,p,T分别为流体的密度、速度q在绝对坐标系下的2个分量、总能、总焓、压强、温度,q,qb分别为流体质点的绝对速度、控制体表面的绝对速度,Ix,Iy分别为惯性系的沿坐标轴方向的单位矢量.
本工作采用中心有限体积格式进行空间离散[4],湍流模型采用Baldwin-Lomax(B-L)模型.
2 POD方法
POD方法的一个重要特点就是可以将相干结构及其包含的能量联系起来,即从能量的角度对速度场进行分析,并识别流场中含有最大能量的模态.POD方法的核心思想[5]就是通过计算得到函数空间{vn(x)∈Ω}的一组“最优”正交基{φ1,φ2,…,φ∞},这里的“最优”意味着使函数投影到正交基上产生的误差达到最小,这一目的等同于以下最优问题:
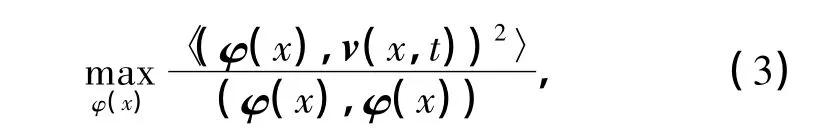
式中,{Ω}为函数空间的定义域,该空间的内积为(·,·),〈·〉表示对集合中n个元素进行算术平均.可以认为集合{vn(x)∈Ω}是不同次实验采集的矢量数据集,也可以认为它是在不同时刻采集的数据集合.用变分方法求解这个最优问题,可以得到如下特征值问题:
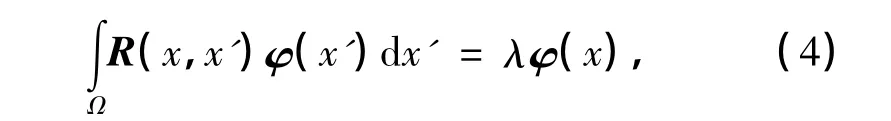
式中,Ω为计算流场域,
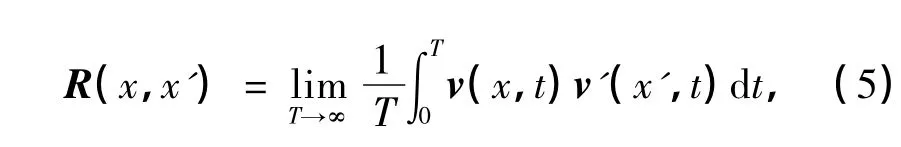
其中R(x,x')为半正定的关系矩阵.同时,由于φi(x)为正交基,所以
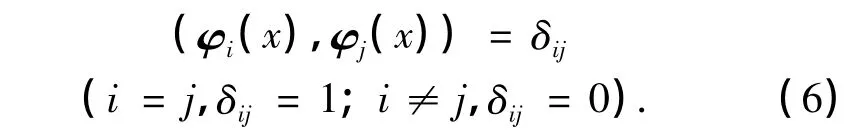
而集合{Vn∈Ω}中的元素都可以由下式表示:
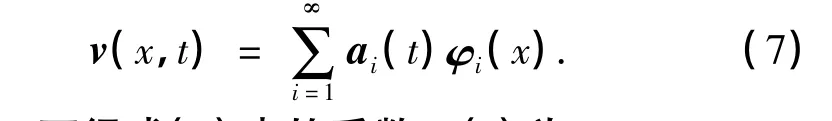
由式(6),可得式(7)中的系数ai(t)为
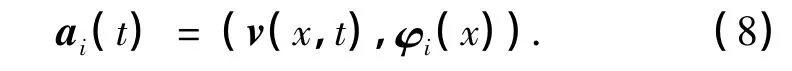
关于POD理论的更多介绍请参见文献[1].
由于本工作中处理的数据集合点数较为庞大,如果直接求解特征问题(4),其求解过程会非常困难.为了解决这个问题,本工作采用Sirovich等[6]提出的快照技术(snapshots)[1],因为该方法能够在很大程度上减少计算对于内存的消耗,即采用原函数空间元素vn的线性组合来表示特征模态,即
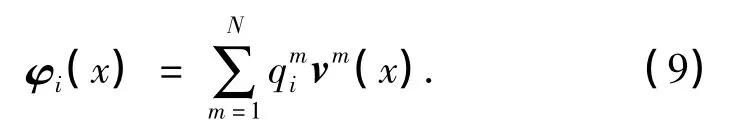
同时,对R(x,x')进行离散,可得
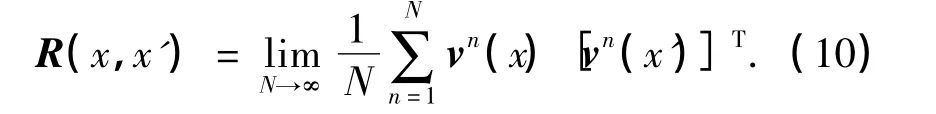
将式(9)和(10)代入式(4),可得
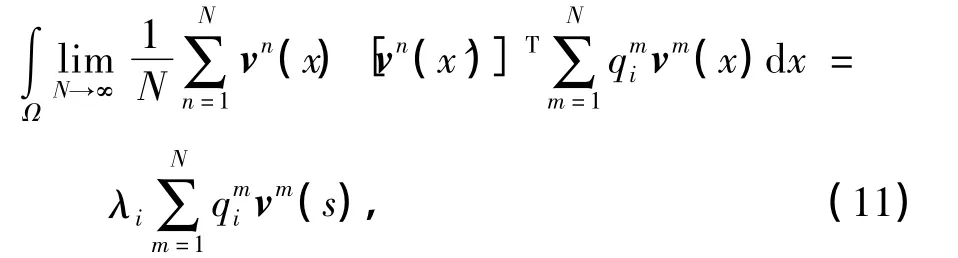
其中当N足够大时,式(11)可化简为
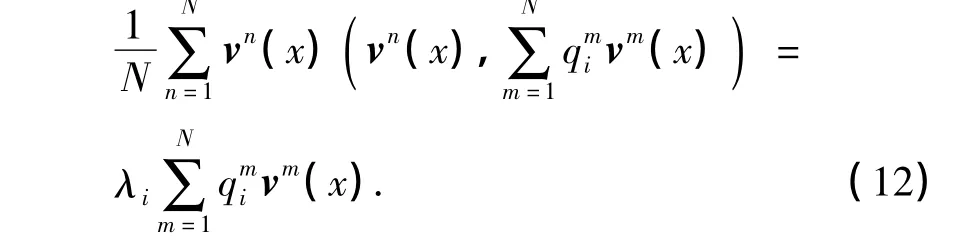
继续简化式(12),可得
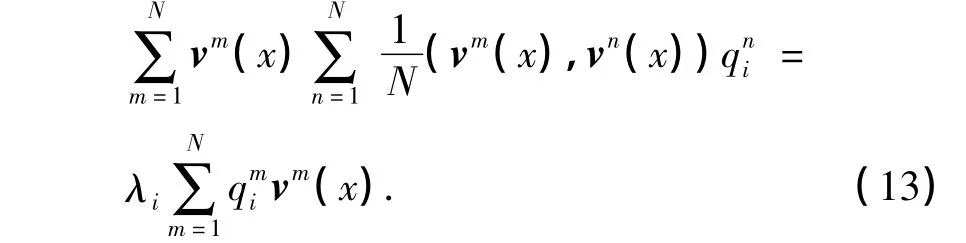
最后,可以得到
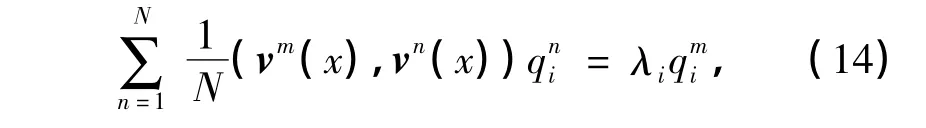
即
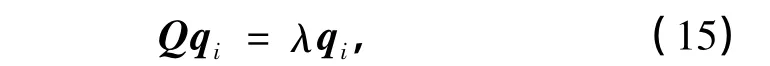
3 嵌套网格与数据筛选和还原
嵌套网格[7]主要包括2个部分:①将计算域分成多个互相有重叠部分的子域,人为地给定重叠区域的内、外边界;②建立各子域间流场信息的传递.
在本工作中,襟翼网格的物面边界条件包括物面无滑移条件、物面绝热壁条件和物面的法向梯度为0.嵌合埋入边界上的流动参数由子域之间的相互干扰来确定,远场边界上每个网格的中心值都由背景网格的流场值插值得到.为实现两段翼型流场间的信息交流,需要在主段翼型流场中给出一个包围襟翼的内边界即嵌合埋入边界,该内边界将襟翼流场的信息传递给主段翼型流场.为此,须定义一个“洞”,该洞的边界围绕襟翼且存在于襟翼网格中.如果主段翼型流场中的点处于该洞中,则称其为“洞中点”;如果主段翼型流场中的点与洞相毗邻且不在洞中,则称其为内边界点或插值点,这样的点就形成了主段翼型流场的一个内边界.洞中点不参与流场的计算,而插值点上的流场参数在计算中不变,且在求解主翼流场之前由襟翼流场插值计算得到.另外,在计算襟翼流场之前,还需通过主翼流场插值计算确定其外边界上的流场参数.
在数据筛选和还原方面,主翼和襟翼均采用静态的嵌套网格[8]系统,即主翼网格和襟翼网格相对静止且对坐标系绝对静止.由于嵌套网格系统的特点,计算时会产生一部分无意义点——洞边界内部和物面内部的点,而这些无意义点若参与snapshots方法后处理分析,则会对正确描述流动结构产生干扰作用.因此,在网格生成过程中,首先,将洞边界内部和物面内部的无意义点进行标记;然后,在应用snapshots方法处理之前,对每个变化时段里的无意义的标记点进行预处理筛选并剔除在计算之外;最后,在通过snapshots方法处理完成有效数据之后,再将洞边界内部和物面内部的无意义点的数据还原至原坐标位置.这样既保证了参与后处理数据的有效性,又保证了分析和对比流场时对应数据的完整性.
4 算例与分析
4.1 方法验证
为了验证本工作snapshots方法的适用性,对曲面方程进行数值重构模拟,设
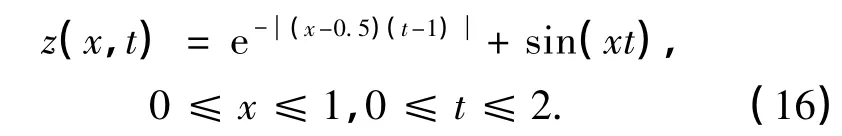
定义空间步长x为均分的25个点,时间步长t为均分的50个点,函数z的原型和重构如图1所示.首先,构造相关矩阵Z=z×z',通过POD方法分解关系矩阵Z,分别对Z进行前三阶的重构拟合.图2为本征模态对应本征值的排列.综上可得,前三阶的模态已经包含了全部能量的99%左右.由图1(d)可以很明显地看出,前三阶模态的重构已经能很好地拟合曲面函数,同时,和文献[9]中的方法相比较可证明本工作snapshots方法的有效性.
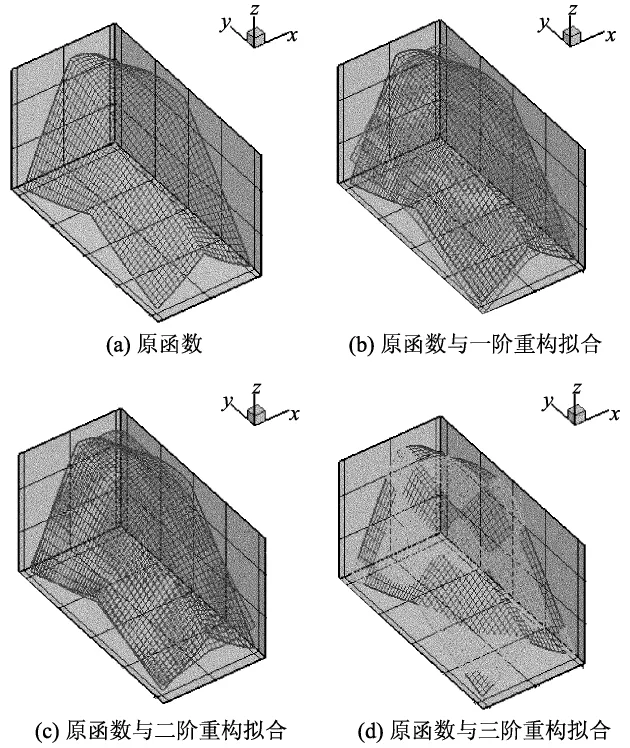
图1 原函数与重构拟合Fig.1 Actual surface and approximation
4.2 迎角变化的多段翼型襟翼的流动数值模拟和POD分析
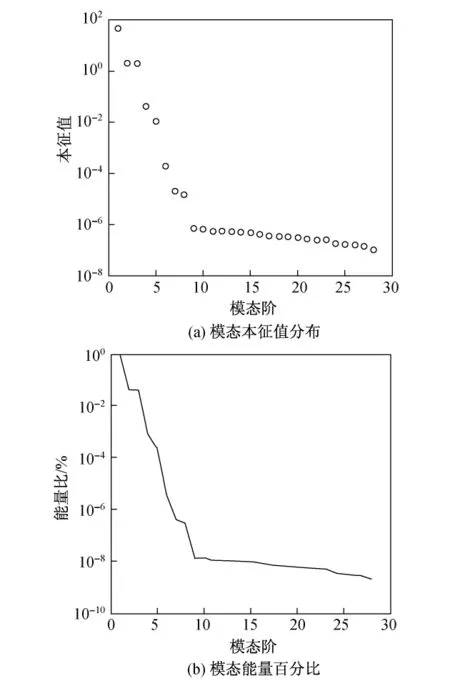
图2 模态能量值Fig.2 Model value
本研究对迎角变化的多段翼型流场进行了数值模拟,选用的多段翼型为带30%襟翼的GAW-2翼型结构.采用的嵌套网格布局如图3所示,对主翼和襟翼分别产生一个C形网格.同时为了保证计算精度,对流动比较剧烈的襟翼仓附近的网格进行横向加密,在2个网格中都建立了人工洞边界.在缝道流动区内都进行纵向局部加密,这样既可以满足缝道流动的粘性特点,又能保证网格嵌套时重叠区有足够的网格层数.算例的来流马赫数Ma=0.3,雷诺数Re=2.2×106,迎角起始角为α=-2°.迎角的变换范围为-2°≤α≤10.8°,变换间隔为Δα=0.2°,共取65个瞬态流场,并且对其进行snapshots分析.图4为迎角变换至10.8°时的瞬态流场,而图5是u,v对应的65阶本征模态各本征值占全部动能的比例.在snapshots计算结果中,占支配地位的本征模态通常代表流场中具有较高动能的大尺度湍流结构.从图中可以看出,在翼型周围的流场中,一阶模态本征值几乎占总动能的87%-u和77%-v,而二阶模态占总动能的大约8%-u和19%-v,三阶模态占总动能的大约2%-u和2%-v.由此可见,高阶模态对总动能的贡献相对较低,因此,可以认为低阶模态是整个流动结构的载体,而较高阶模态则包含了小尺度的复杂流动结构的信息.

图3 嵌套C形网格Fig.3 Overlapped C-grid
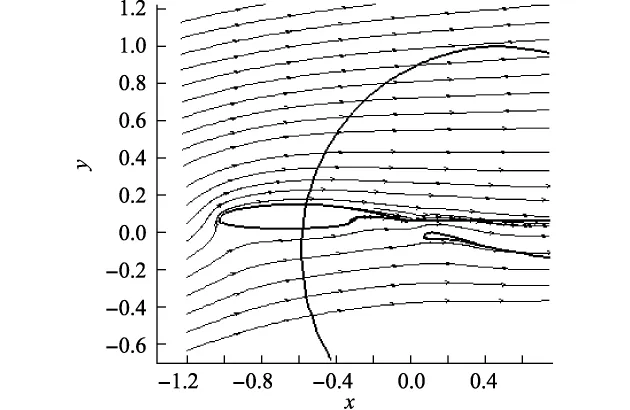
图4 原流场Fig.4 Original flow field
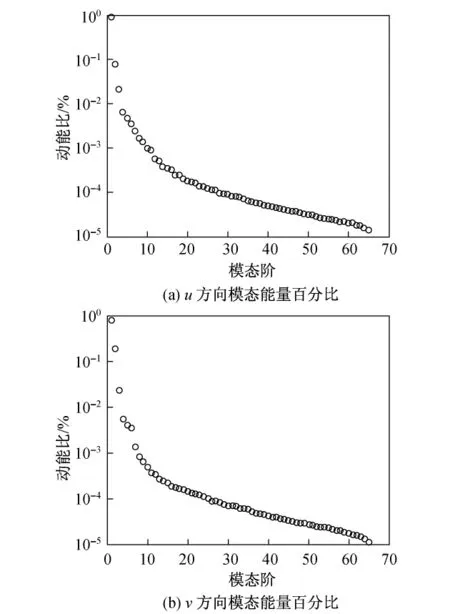
图5 模态能量百分比Fig.5 Modal value percentage

图6 三阶重构流场Fig.6 Rank 3 approximation of flow field
由于u,v的前三阶模态分别包含了总能量的97%和98%,因此,由前三阶模态重构的流场已经涵盖了整个流场的绝大多数的能量,与原流场拟合得很好(见图6).图7为前三阶本征模态的速度场,每个模态代表包含在流动中的不同尺度的流动结构:①一阶模态代表流动中包含了绝大部分能量的结构,它的流动结构就是平均流,同时在每个模态中,主翼和襟翼缝隙间都出现了涡旋结构,因此,同平均流一样,在主翼和襟翼缝隙间出现的涡旋在整个变化过程中对流场的影响起主要作用;②二阶模态中主翼的头部、尾部和襟翼的下方有3条明显的分离线,而在主翼上方出现了明显的顺时针脱体涡,同时,由于二阶模态中v方向上占总能量比重相对要大,所以速度场受v的影响要大,因此,由图7(b)可以发现,整个流动结构呈向上环流形态;③三阶模态同样在主翼的前上方和尾部上方有2条较为明显的分离线,在分离线之间形成逆向的回流,且回流结构位置与二阶模态中出现的脱体涡位置几乎一致,但流动方向相反.而涡旋结构则主要出现在主翼和襟翼的尾部,由图7(c)可以看到2个明显的尾涡.图8为u,v方向的前三阶模态权重在整个变化过程的分布规律.可以发现,低阶模态所含能量与迎角变化有弱相关性,而随着模态阶数的上升,高阶模态所占能量对于迎角变化十分敏感,即不同的小尺度复杂脉动结构对于整个流场的影响会随着迎角的变化而变化,而大尺度的流动结构的影响随迎角的变化相对不明显.
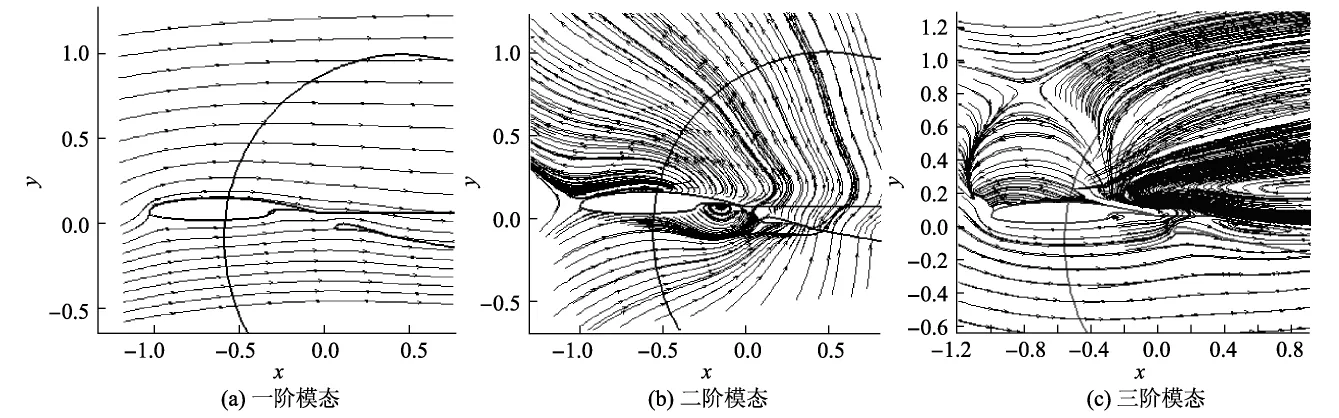
图7 前三阶模态Fig.7 Modals of the first three rank
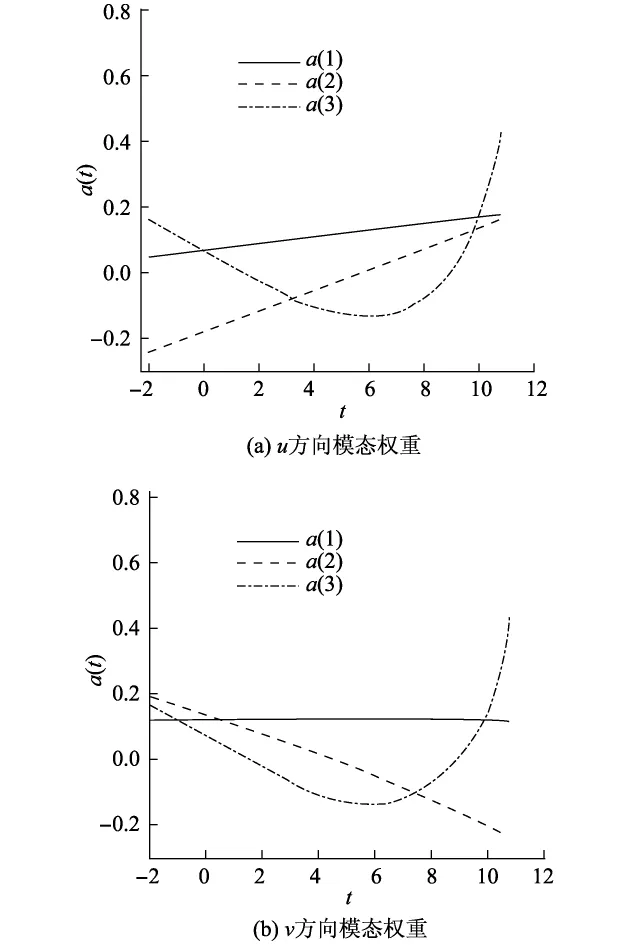
图8 模态权重Fig.8 Modal weight
5 结论
本工作通过嵌套网格技术对迎角变化情况下的多段翼型主翼和襟翼周围的流场进行了数值模拟,并对连续采集的瞬态速度场进行筛选处理;最后,将具备研究意义的数据点进行POD后处理统计分析.通过研究,得到如下结论.
(1)POD方法不同,内积方式的选择对结果分析不会产生本质的影响,但对结果的收敛速度和模态分析会产生一定的影响.本工作采用了将u,v分离的能量内积方法对多段翼型主翼和襟翼周围的速度场进行POD分析,相对减缓能量谱的收敛速度,以确保低阶模态具有较为简单的结构,这样更有利于对流场的分析.对于POD方法而言,内积方式的选取不存在单一的准则,可以根据研究需要进行选取.
(2)迎角变化情况下的多段翼型主翼和襟翼周围的流场平均流占据总能量的绝大部分,因而通过POD处理后,第一阶模态捕捉到的结构就是平均流,其他模态分析的是脉动结构.随着模态阶数的升高,POD所捕捉的流场结构更为复杂和不规则,分布在模态间的能量收敛开始变慢,即高阶模态所捕捉到的复杂结构对于总体的影响开始趋向于平均,各自占有的能量比重十分接近.
(3)利用POD方法能进一步获得隐藏在平均流场背景中低阶模态的复杂相干结构.同一位置在二、三阶模态中分别出现了顺时针脱体涡结构和逆向流动结构,但由于脱体涡出现在更低阶的模态中,因此,其对整个流场的影响更大.而同样对流场影响较大的还有主翼和襟翼的尾部出现的同向尾涡.
[1] WANGA X,MAY C,YANW J.The proper orthogonal decomposition method for Navier-Stokes equations[J].ACAD J XJTU,2008,20(3):141-148.
[2] VOLKWEINS.Proper orthogonal decomposition(POD) for nonlinear dynamical systems [R]. Austria:University of Graz Disc Summerschool,2005:1-26.
[3] 李孝伟.基于嵌套网格的全机带襟、副翼绕流的数值模拟[D].西安:西北工业大学,1999:8-10.
[4] JAMESONA,SCHMIDTW,TURKELE.Numerical solution of the Euler equations by finite volume methods with Runge-Kuuta time stepping schemes[C]∥ AIAA Paper.1981:81-1259.
[5] 杨琴,符松.超音速平面混合层的POD分析[J].中国科学:G辑,2008,38(3):319-336.
[6] EVERSONR,SIROVICHL.Karhunen-Loeve procedure for gappy data[J].J Opt Soc Am,1995,12(8):1657-1664.
[7] BENEKJ A,BUNINGP G,STEGERJ L.A 3-D chimera grid embedding technique[C]∥ AIAA Paper.1985:322-331.
[8] 杜超.多段翼型非定常粘性绕流数值研究[D].上海:上海大学,2007:22-29.
[9] CHATTERJEE A. An introduction to the proper orthogonal decomposition[J].Current Science,2000,78(7):808-817.
