具有给定分支数森林的最小能量图
2012-01-31王文环
王文环
(上海大学理学院,上海200444)
图是图论的基本研究对象,与分子图有密切的联系.从20世纪上半叶以来,图的研究与化学建立了新的联系,人们发现Hückel分子轨道理论与图的谱之间存在明确的对应关系[1].
令G为具有n个顶点的分子图,A(G)是其连接矩阵,G的特征多项式[2]为
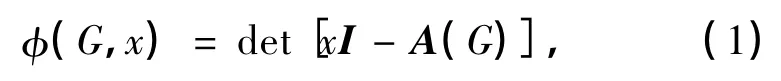
式中,I为n阶单位矩阵.记φ(G,x)=0的n个根为λ1,λ2,…,λn,即为相应图G的特征根.在Hückel分子轨道(Hückel molecular orbital,HMO)意义下,将图G的能量E(G)[3]定义为
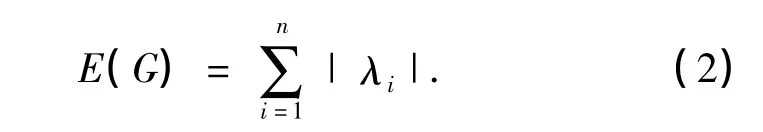
E(G)是共轭分子的一个重要参数,是共轭分子的化学结构和热力学稳定性之间的桥梁.图的能量越大(小),相应化合物的热力学稳定性越强(弱)[3].因此,研究具有极值能量的图及其排序是化学图论中的重要课题之一[4-5],在理论化学中具有重要的意义.关于E(G)的详细介绍可参见文献[3].
令m(G,k)为图G的k匹配数,即G中k条互不相邻的边的个数,其中0≤k≤[n/2].为了方便,令m(G,0)=1.对具有n个顶点的森林F,其能量可以表达成下面的Coulson积分公式[3]:
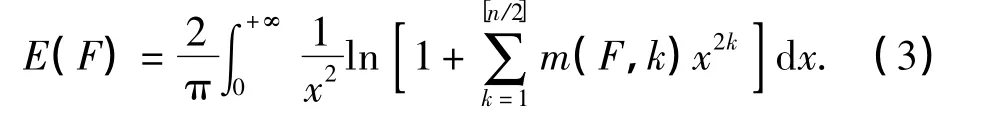
由式(3)可知,E(F)是m(F,k)的单调递增函数,其中1≤k≤[n/2].因此,对于2个森林F1和F2, Gutman等[6-7]定义了如下拟序关系:
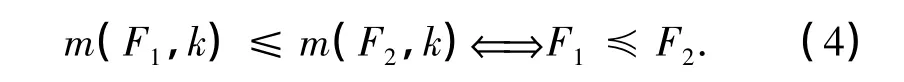
若F1≾F2,且至少存在一个整数k,使得m(F1,k)<m(F2,k),则有F1≺F2.若对所有 k,m(F1,k)= m(F2,k),则F1≅F2.若F1≺F2和F1≻F2都不成立,则称F1和F2不可比.根据式(3)和(4),若F1≾F2,则 E(F1)≤E(F2);若 F1≺F2,则 E(F1)<E(F2).
利用上述拟序关系可得到一些无圈图在给定顶点时的极值能量图.比如,对于树,Gutman[6]得到了前4个具有较小能量的树和具有最大能量和次大能量的树;Li等[8]刻画了第5小和第6小能量树; Wang等[9]得到了前9个具有较小能量的树.对具有完美匹配的树,Zhang等[10]得到了前3个具有较小能量的树;Guo[11]刻画了前5个具有较小能量的树; Wang等[12]得到了前11个具有较小能量的树.对给定直径的树,Yan等[13]得到了最小能量树;Zhou等[14]得到了第2小能量树.对具有给定悬挂顶点数的树,Yu等[15]得到了最小能量树.对具有给定匹配大小的树,候耀平[16]刻画了最小和次小能量树.对具有给定非悬挂边数的树,王霄霞等[17]得到了最小和次小能量树.
记Fn,q为具有n个顶点和q个分支的森林的集合,其中q≥1.由于森林的每个分支是顶点个数不少于2的树,因此n≥2q.特别地,当q=1,Fn,q为具有n个顶点的树的集合.当n和q给定时,本工作确定了Fn,q中具有最小能量的图.
1 预备工作
为了得到本工作的结论,下面引入一些图的定义和引理.
令Pn为具有n个顶点的路,sPn为s条Pn的并,其中s为不小于2的正整数,K1,n-1为具有n个顶点的星图.
引理1[3]令e=uv为G中的一条边,则有
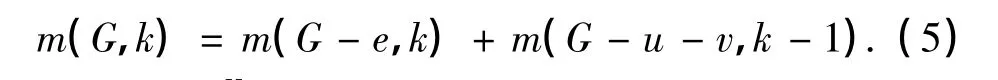
引理2[6]令T为具有n个顶点的树,当n≥4时,有K1,n-1≾T,等号成立当且仅当T=K1,n-1.
2 主要结果
定理1 设F∈Fn,q,其中1≤q≤n/2,且n≥4,则有E(K1,n-2q+1∪(q-1)P2)≤E(F),等号成立当且仅当F=K1,n-2q+1∪(q-1)P2.
证明 当q=1时,Fn,q为具有n个顶点的树的集合.由引理2可知,定理1成立.
当q≥2时,由式(4)可知,只要证明
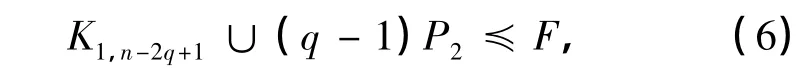
等号成立当且仅当F=K1,n-2q+1∪(q-1)P2.
下面对n用数学归纳法证明定理1成立.
当n=2q和2q+1时,由于F∈Fn,q,因此,F分别为qP2和P3∪(q-1)P2.显然式(6)的等号成立.
当n=2q+k,k≥2时,设式(6)成立.
下面证明当n=2q+k+1时,式(6)成立.
由于F∈Fn,q,令F=T1∪T2∪…∪Tq,其中Ti为顶点个数不少于2的树,1≤i≤q.由于n=2q+ k+1,且k≥2,因此,在F中必有一个顶点个数不少于3的分支.不失一般性,假设此分支为Tq.令uv为K1,n-2q+1∪(q-1)P2中分支K1,n-2q+1的一条边,u'v'为F中分支Tq的一条悬挂边.由引理1,有
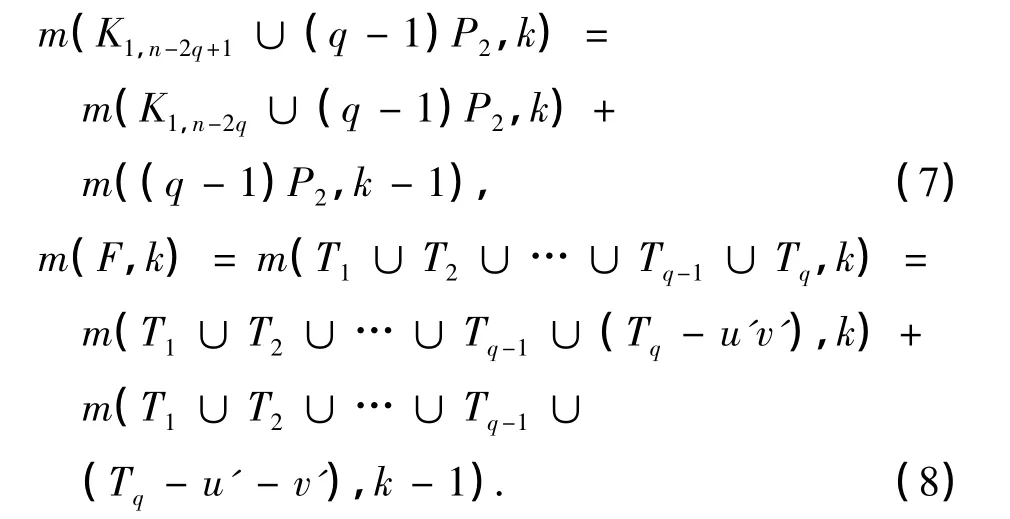
由于树Tq的顶点个数不少于3,因此,Tq-u'v'为顶点个数不少于2的树.所以 T1∪T2∪…∪Tq-1∪(Tq-u'v')为具有q个分支且顶点数为n-1的森林.由归纳假设,有
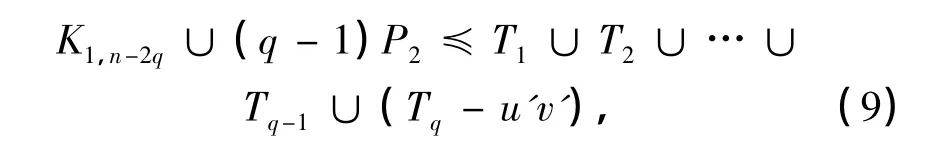
等号成立当且仅当T1∪T2∪…∪Tq-1∪(Tq-u'v')= K1,n-2q∪(q-1)P2.
又由于当1≤i≤q-1时,Ti为顶点个数不少于2的树,因此,有P2≾Ti.所以
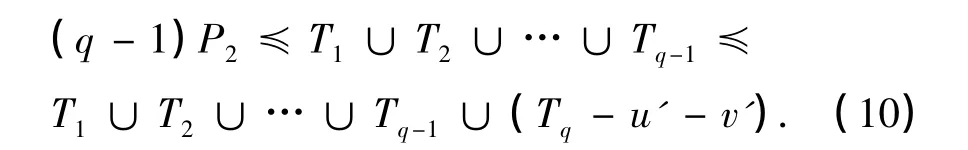
式中第1个等号成立当且仅当对所有1≤i≤q-1,Ti=P2;第2个等号成立当且仅当Tq-u'-v'是孤立点的集合.
由式(9)和(10),比较式(7)和(8),当n=2q+ k+1时,式(6)成立,且式(6)等号成立当且仅当式(9)和(10)中的所有等号同时成立,即Ti=P2且Tq=K1,n-2q+1,其中1≤i≤q-1.因此,定理1成立.
[1] 张福基.图依能量的排序[J].厦门大学学报:自然科学版,2001,40(2):157-162.
[2] CVETKOVICD M,DOOBM H S.Spectra of graphs theory and application[M].New York:Academic Press,1980.
[3] GUTMANI,POLANSKYO.Mathematical concepts in organic chemistry[M].Berlin:Springer-Verlag,1986.
[4] 唐熬庆,江元声.分子轨道图形理论[M].北京:科学出版社,1980.
[5] CAPOROSSIG,CVETKOVICD,GUTMANI.Variable neighborhood search for extremal graphs.2.finding graphs with extremal energy[J].Journal of Chemical Information and Computer Sciences,1999,39:984-996.
[6] GUTMANI.Acyclic systems with extremal Hückel πelectron energy[J].Theoretica Chimica Acta,1977,45:79-87.
[7] GUTMANI,ZHANGF.On the ordering of graphs with respect to their matching numbers[J].Discrete Applied Mathematics,1986,15(1):25-33.
[8] LIN N,LIS C.On the extremal energies of trees[J].MATCH-Communications in Mathematical and in Computer Chemistry,2008,59(2):291-314.
[9] WANGW H,KANGL Y.Ordering of the trees by minimal energies [J]. Journal of Mathematical Chemistry,2010,47(3):937-958.
[10] ZHANGF,LIH.On acyclic conjugated molecules with minimal energies[J].Discrete Applied Mathematics,1999,92(1):71-84.
[11] GUOJ M.On the minimal energy ordering of trees with perfect matchings[J].Discrete Applied Mathematics,2008,156(14):2598-2605.
[12] WANGW H,KANGL Y.Ordering of the trees with a perfect matching by minimal energies[J].Linear Algebra and Its Applications,2009,431:946-961.
[13] YANW G,YEL Z.On the minimal energy of trees with a given diameter[J].Applied Mathematics Letters,2005,18(9):1046-1052.
[14] ZHOUB,LIF.On minimal energies of trees of a prescribed diameter[J]. JournalofMathematical Chemistry,2006,39(3/4):465-473.
[15] YUA M,LÜX Z.Minimum energy on trees with k pendent vertices [J]. Linear Algebra and Its Applications,2006,418(2/3):625-633.
[16] 侯耀平.具有给定匹配大小的极小能量树[J].系统科学与数学,2003,23:491-494.
[17] 王霄霞,郭晓峰.关于具有给定非悬挂边数的树的极小能量[J].数学研究,2006,39:109-116.
