大圆筒结构-土-波浪相互作用的动力响应分析

汪德江， 叶志明

(上海大学土木工程系，上海200072)

目前，随着人类对近海及外海资源的不断开发，我国的近海港口工程建设发展迅速，已涌现出了一批适应深海港口工程的新型结构形式，其中包括沉入式大直径薄壳圆筒结构.该结构不仅能适应水深浪大的恶劣环境，而且可以在不需对软土地基进行处理的情况下直接插入地基土.尤其对于淤泥质软土的深海地基，该结构有不可替代的优势.然而，由于沉入式大直径薄壳圆筒结构的受力机理比较复杂，需要考虑结构与周围土体的共同作用，同时该结构又长期受到波浪力的作用，因此，到目前为止，对于定量分析模型及物理力学计算模式，还没有相关的能够得到工程界认可的工作机理，对此结构的计算也没有相应的国家规范.因此，合理地计算分析新型的大直径薄壳圆筒结构，已成为港口及水运工程研究领域的热点与难点.

国内外诸多学者已对沉入式大直径薄壳圆筒结构进行了研究［1-11］.范庆来等［3］提出一种准三维上限分析方法，证实了大圆筒的破坏与经典水工结构的破坏是不同的;王乐芹等［4］建立了横向荷载作用下的大圆筒结构的上限法极限分析模型，以求解大直径薄壳圆筒结构上的横向极限荷载;王刚等［5］通过有限元分析，得到大圆筒结构在指定波浪条件下的荷载-位移关系曲线，由此确定结构抗倾覆稳定的安全系数;钱荣等［6］应用多元线性回归方法分析多个变量之间的线性相关关系，得到施工状态下波浪荷载的计算公式;Bai等［7］基于线性波理论，应用边界单元法建立了连续式大圆筒结构的一种反射波数值模型;潘厚志等［8］分别采用壳单元和沿深度分层施加的三维空间弹簧单元模拟大直径圆柱壳结构及其土体，这种壳单元和弹簧单元的耦合数值处理可有效地模拟出圆柱壳结构与土体之间的非线性相互作用机制;Baranyi［1］采用数值方法模拟了大圆筒结构的椭圆率对波浪能量传递到大圆筒结构上的影响;Dong等［2］通过理论分析方法研究了船行经大圆筒结构时，所激起的波浪对圆筒结构的影响.但是到目前为止，同时考虑大圆筒结构-土-波浪的相互作用，并分析其动力特性的研究还鲜有报道.因此，本研究建立了大圆筒结构-土-波浪相互作用的三维非线性有限元模型，并对大圆筒结构的动力特性进行了深入探讨.

1 非线性接触面模型与土的本构模型

由于圆筒薄壳结构与土的变形及强度特性相差较大，因此，在外力作用下，2种材料的接触面之间将产生相对错动、滑移或开裂.为数值计算的准确性，本研究在2种材料之间增设接触面单元，并假设各土层面之间始终保持粘结接触，能够协调变形.

为了说明圆筒薄壳结构与土之间的相对滑动，本研究采用有限元的罚函数法来模拟桩-土之间的接触问题.通过在桩-土界面处设置主-从接触，采用扩展的Mohr-Coulomb摩擦模型进行接触分析，桩-土之间的摩擦力由下式确定：

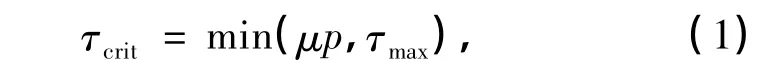
式中，μ=tan δ为摩擦系数，p为接触面上的压力，τmax为用户指定土层的极限摩擦阻力.δ为桩-土之间的摩擦角，它是影响摩擦桩承载性能的关键因素，具体采用Randolph等［12］建议的如下计算式来估算：

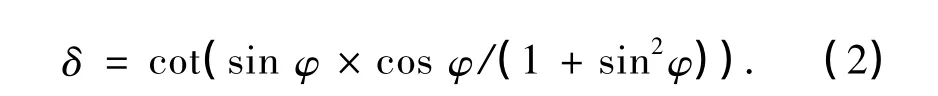
由于土体的摩擦角范围为15°～30°，因此取δ的范围为13.2°～19.1°，则摩擦系数μ=0.234～0.346.由于圆筒薄壳结构与土的模量相差较大，因此，模拟过程中假设结构为理想弹性材料，土体为符合Mohr-Coulomb屈服准则的弹塑性材料.

Mohr-Coulomb屈服准则假定如下：当作用在某一点的剪应力等于该点的抗剪强度时，该点发生破坏，剪切强度与作用在该面的正应力呈线性关系.图1为Mohr-Coulomb破坏模型，其强度准则如下：

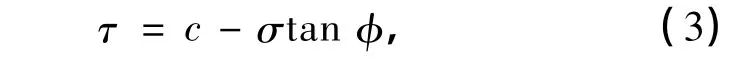
式中，τ为剪切强度，σ为正应力(σ1为大主应力，σ2为中主应力，σ3为小主应力)，c为材料的粘聚力，φ为材料的内摩擦角.

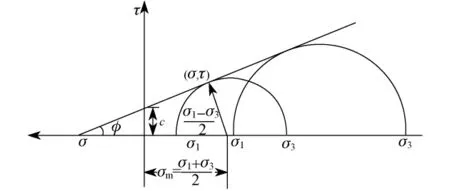
图1 Mohr-Coulomb破坏模型Fig.1 Mohr-Coulomb failure model

从Mohr圆可以得到以下关系：

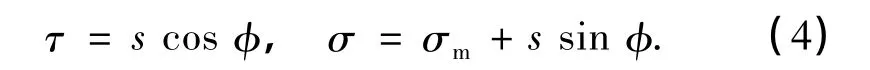
把τ和σ代入式(4)，则Mohr-Coulomb准则可写成

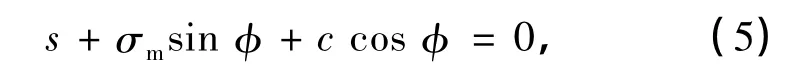
式中，s=(σ1－σ3)/2为大、小主应力差的一半(即为最大剪应力)，σm=(σ1+σ3)/2为大、小主应力的平均值.Mohr-Coulomb准则假定材料的破坏和中主应力无关.

2 数值模型的建立

2.1 结构方案

大圆筒结构直径12 m，筒体为钢筋混凝土结构(砼强度等级 C60)，基础筒高 22 m，基础壁厚25 cm，露出土体以上部分7 m，大圆筒质量470 t.筒顶高程▽1.5 m，筒底高程▽－23.5 m，即初始筒高22 m，埋入部分15 m.

2.2 荷载要素

大圆筒在实际工作时可能会遇到不同大小的荷载，其中波浪荷载合力可根据实际工况的波浪要素计算得到，具体计算公式为

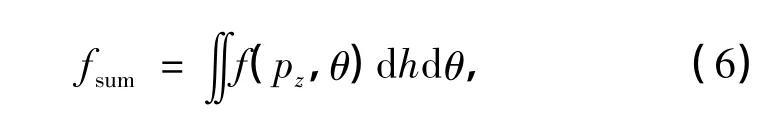
式中，f(pz，θ)=pzsin θ，其中pz为直立平面墙上、静水面以下深度z(m)处的波浪压力强度(kPa).

按照实际工况中波浪荷载取值范围(1 000～8 000 kN)对波浪荷载合力进行取值，变化增量为1 000 kN.

2.3 有限元模型

为模拟实际工程中大直径圆筒结构在动力作用下的受力工作状态，在有限元模型中建立5个间距为0.8 m的连续筒结构，以模拟筒与筒之间的相互影响.考虑模型土体的真实性，计算区域为长方体，土体深度设为5倍大圆筒结构高度，宽度设为5倍大圆筒结构直径.应用大型的通用有限元软件ANSYS进行分析，大圆筒和土都采用solid45单元，单元数为216 356，土体和大圆筒接触面上均设接触面单元，接触面摩擦系数取0.3.

2.4 材料参数

土体的密度为1 800 kg/m3，弹性模量为96.3 MPa，泊松比为0.3，粘聚力为26 kPa，内摩擦角为15°.钢筋混凝土密度为2 500 kg/m3，弹性模量为36 MPa，泊松比为0.167.

2.5 边界条件

地基土边界四周约束为ux=uy=0，底部对三向自由度全部约束，即ux=uy=uz=0.对大圆筒采用动力分析中的瞬态分析，波浪荷载设为随时间变化的正弦函数，周期为1.57 s，采用面荷载的形式施加.动力分析中的阻尼采用比例阻尼，由质量和刚度阻尼组合而成.大圆筒有限元计算模型如图2所示.

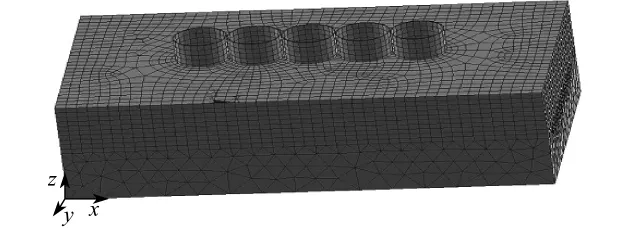
图2 大圆筒整体网格划分模型(埋深15 m)Fig.2 Global mesh generation model for large cylinder structure(buried depth=15 m)

3 计算和分析

3.1 数值模拟

大直径圆筒的埋深和筒壁厚度是影响筒壁应力的关键因素，为了研究嵌固深度对结构强度的影响，对埋深段及筒高以2 m为步长分别建模计算，埋深依次为15，17，19，21，23 m，相应筒高为22，24，26，28，30 m，厚度分别为0.20，0.25，0.30，0.35，0.40 m.动力计算取2个周期，周期内筒壁上应力的坐标如图3所示，随时间的变化如图4和图5所示.对不同波浪力、埋深、筒壁厚度下最大应力变化进行数值模拟，计算结果如表1～表4(表中仅列出部分计算结果)及图6～图8所示.

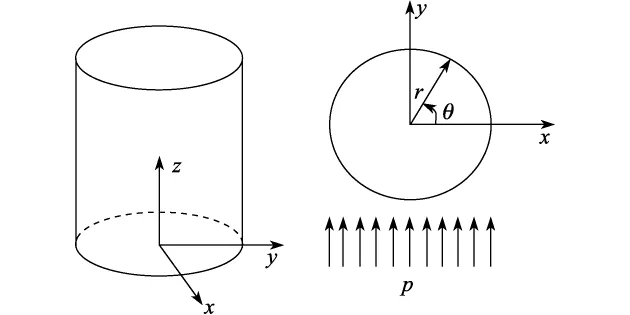
图3 坐标示意图Fig.3 Coordinate schematic diagram

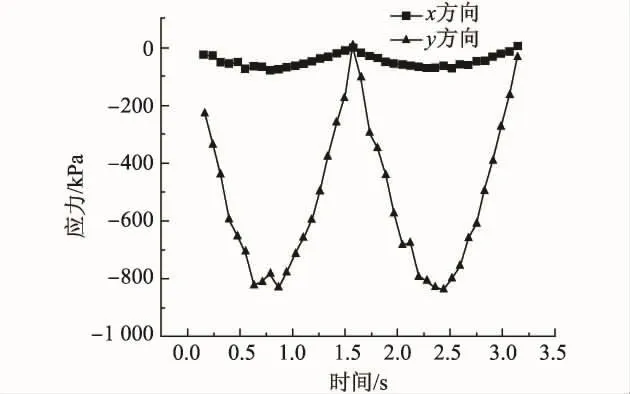
图4 z=22 m，θ=180°处的应力时程Fig.4 Diagram of the stress-time history(z=22 m，θ=180°)

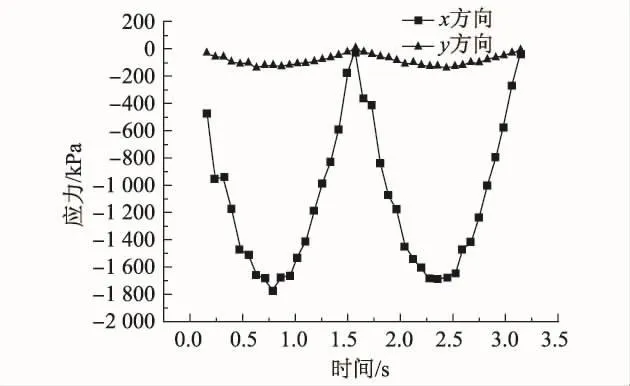
图5 z=22 m，θ=270°处的应力时程Fig.5 Diagram of the stress-time history(z=22 m，θ=270°)

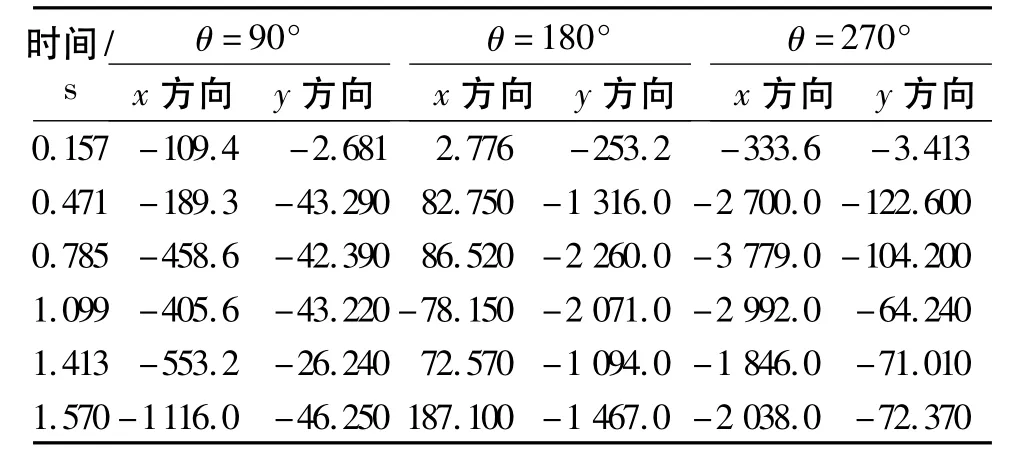
表1 不同时间下z=0 m处的应力Table 1 Stress at z=0 m for different time kPa

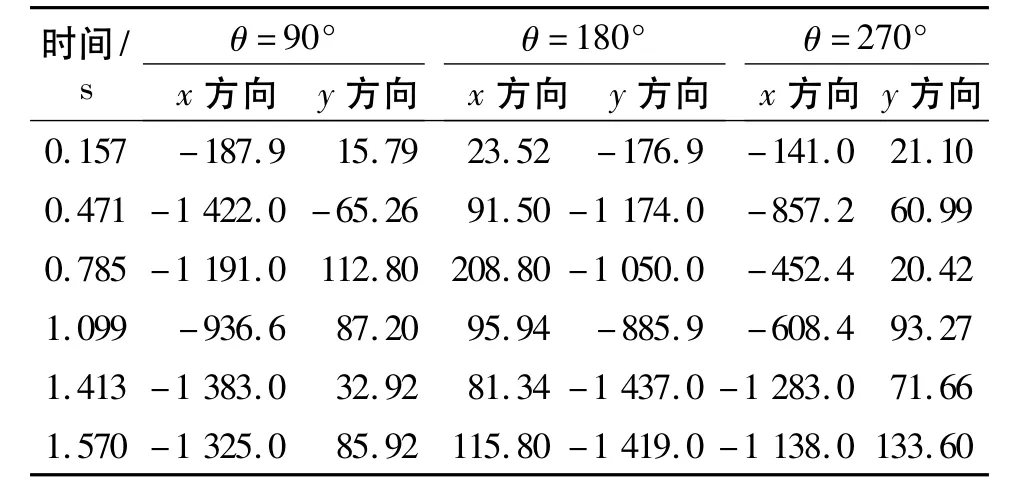
表2 不同时间下z=6 m处的应力Table 2 Stress at z=6 m for different time kPa

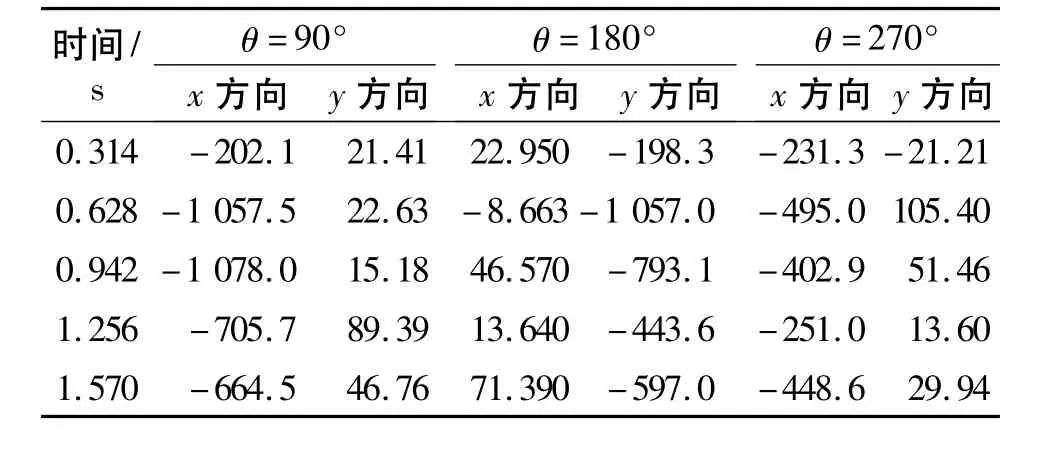
表3 不同时间下z=15 m处的应力Table 3 Stress at z=15 m for different time kPa

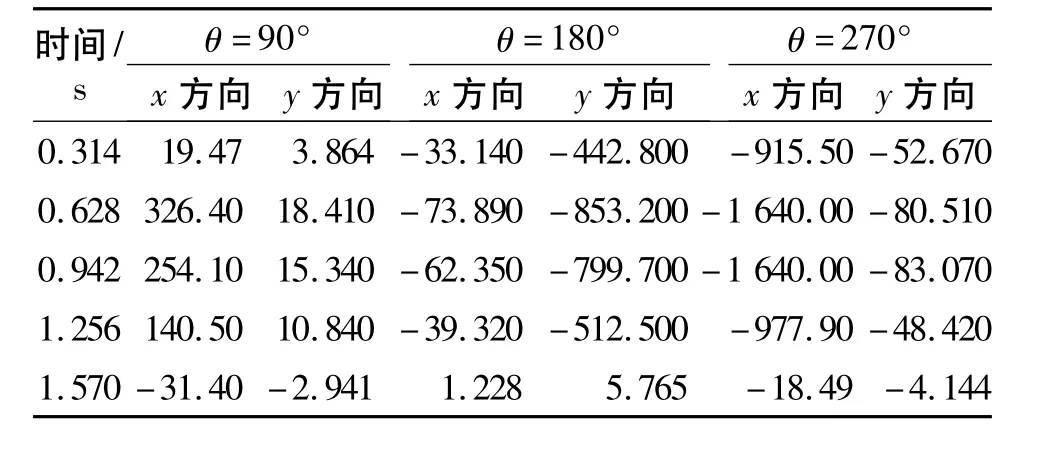
表4 不同时间下z=22 m处的应力Table 4 Stress at z=22 m for different time kPa

由图3和图4可知，x，y方向应力呈周期变化，x方向应力周期变化幅值比y方向小，x方向基本上处于0应力状态，而y方向应力周期变化巨大，最大值达到1 800 kPa.x方向应力随内摩擦角度变化不敏感，y方向应力随内摩擦角度有10%左右的变化.由图5可知，x，y方向应力随着波浪力的增大而增大，接近线性变化.由图6可知，随着埋深增加，x，y方向应力总体上减小，但在一定深度处出现应力峰值，而且y方向应力小于x方向应力.由图7可知，随着壁厚增加，x，y方向应力减小，变化曲线的形状接近反比例曲线.当壁厚达到一定值时，应力趋向稳定，不再随壁厚增加而减小.

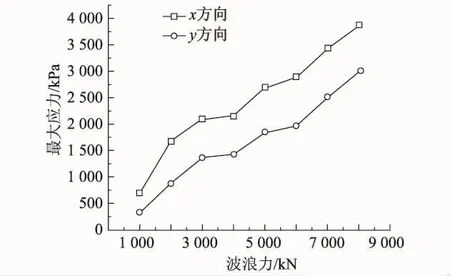
图6 不同波浪力下的最大应力Fig.6 Maximum stress for different wave

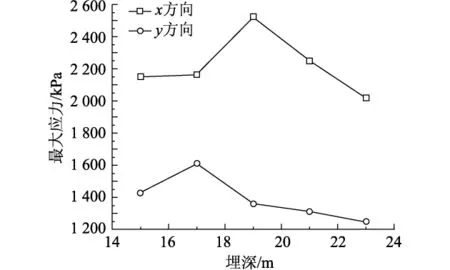
图7 不同埋深下的最大应力Fig.7 Maximum stress for different buried depth

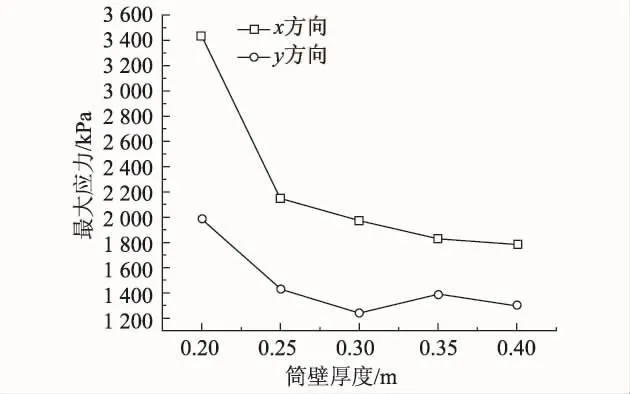
图8 不同筒壁厚度下的最大应力Fig.8 Maximum stress for different thickness

3.2 应力分布函数的确定及筒壁最大应力分析

通过数值计算结果，利用多元回归分析，可得出在波峰行近时筒壁上x，y方向的最大应力分别如下：

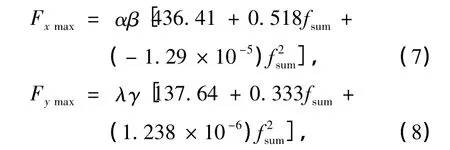
式中，α=－2.15+0.35h－0.009 2h2为x方向最大应力的埋深修正系数，β=4.89－23.44t+33.49t2为x方向最大应力的厚度修正系数，λ=1.41－0.023h为y方向最大应力的埋深修正系数，γ=3.82t－17.54t+25.97t2为y方向最大应力的厚度修正系数.

4 结论

大圆筒薄壳结构是一个空间圆柱形壳体结构体系，因其受力条件复杂，受到的荷载是非单一、非均一、非静态的.同时，由于要考虑到地基土体(线性与非线性情况)的相互作用，以及结构与土体的相互作用、共同变形的工作机理，因此，薄壳圆筒结构的强度计算不能沿用经典水工结构的计算模式.到目前为止，一般的结构力学解析方法均难以得到合理的结果.为了使结构计算模式能够更好地符合实际原型结构及其工作状态，能较为真实地反映结构的强度问题，本研究由数值计算结果得出了如下几个在实际工程中多筒情况下的筒壁最大应力的变化规律.

(1)本研究通过对不同波浪力、埋深、筒壁厚度下最大应力的数值计算结果，利用多元回归分析，得出在波峰行近时筒壁上x，y方向的最大应力计算公式，从而可以直接计算得到大圆筒的最大应力，给工程设计带来极大方便.

(2)最大应力一般出现在自由端，x方向最大应力一般出现在与x正方向夹角为90°处，y方向最大应力出现在与x正方向夹角为180°处.从受力特点分析，在嵌固泥面处，90°处变形最大，土体抗力随着圆筒结构弧形变化而逐渐变大，导致在该处产生最大应力;而在180°处，土体对筒壁的摩擦力较大，使得沿y方向应力较大.

(3)最大应力随波浪力的增大基本呈线性增大趋势.当自由端的高度不变，埋深增加时，最大应力先增大后减小，但是x和y方向达到最大应力时的埋深不一样.总体趋势是随着埋深的增加，最大应力减小.这表明埋深增加对大圆筒的应力有一定消散作用.

(4)随着壁厚的增加，大圆筒筒壁最大应力明显减小，当壁厚达到一定值时，应力趋向稳定，不再随壁厚增加而减小.虽然壁厚对x和y方向最大应力的影响程度是不一样的，但都是当壁厚达到0.35 m时，应力趋于稳定.通过对大圆筒结构的强度分析，可得出较为合理的壁厚尺度为0.012 5筒高.

［1］ BARANYIL.Numerical simulation of flow around an orbiting cylinder at different ellipticity values［J］.Journal of Fluids and Structures，2008，24(6)：883-906.

［2］ DONGG H，SUN L.Numerical analysis of shipgenerated waves action on a vertical cylinder［J］.Journal of Ship Research，2009，53(2)：93-105.

［3］ 范庆来，栾茂田，杨庆.横观各向同性软基上深埋式大圆筒结构水平承载力分析［J］.岩石力学与工程学报，2007，26(1)：94-101.

［4］ 王乐芹，周锡礽，张伟.软粘土中插入式大直径薄壁圆筒结构的一种极限状态分析模型［J］.海洋技术，2005，24(1)：95-100.

［5］ 王刚，陈杨，张建明.大圆筒结构倾覆稳定分析的有限元法［J］.岩土力学，2006，27(2)：238-241.

［6］ 钱荣，周锡，张建辉.作用于圆柱壳结构上波浪力的多元线性回归分析［J］.港工技术，2001(3)：1-3.

［7］ BAIZ G，ZHOUX R，SUNK L，et al.Numerical model of wave forces on continuous cylinder structures［J］.Transactions of Tianjin University，2001，7(2)：71-75.

［8］ 潘厚志，孙克俐，周锡礽，等.大直径圆柱壳结构与土体相互作用的一种耦合数值模拟方法［J］.港口工程，2000(1)：26-30.

［9］ ZHUG，BORTHWICKA G L，TAYLORR E.A finite element model of interaction between viscous free surface waves and submerged cylinders ［J］. Ocean Engineering，2001，28(8)：989-1008.

［10］ SILLSG，FERGUIO，SVANOEG.Behavior of a model breakwater element on a sandy seabed［J］.International Journal of Offshore and Polar Engineering，2001，11 (4)：241-247.

［11］ LIUH X.Frequency domain analysis of dynamic wave pressures on deeply embedded large cylinder structures due to random waves［J］.Transactions of Tianjin University，2003，9(1)：21-28.

［12］ RANDOLPHM F，WORTHC P.Application of the failure state in undrained simple shear to the shaft capacity of driven piles［J］.Geotechnique，1981，31(1)：143-157.