二维轴对称压差方程组活塞问题的激波解
2012-01-31豆艳萍汤忠飞徐玉兰
豆艳萍, 汤忠飞, 徐玉兰
(上海大学理学院,上海200444)
考虑二维压差方程组
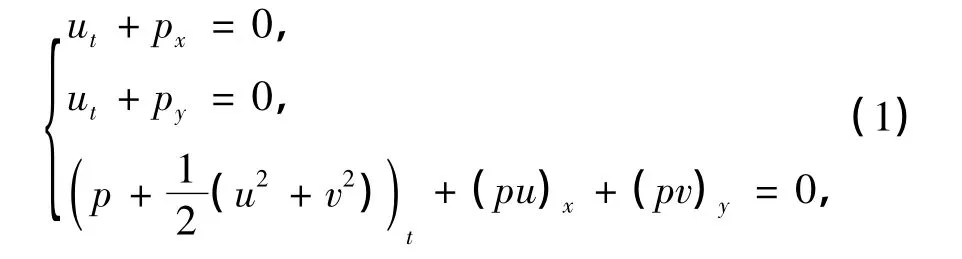
式中,(u,v)为速度,p≥0为压强.当流体内部影响与压强梯度相比较小,并且可以忽略时,方程组(1)是有意义的[1].在研究二维压差方程组(1)的活塞问题(一维活塞问题可参见文献[2])时,一维问题中的活塞事实上为一个边界可移动的物体,管子则变成了整个空间.陈恕行[3]首先研究了高维活塞问题,并证明了当活塞匀速运动时高维位势流方程组激波解的存在性.在此基础上,陈恕行、王泽军等[4-6]研究了二维轴对称等熵Euler方程组激波解的整体存在性.对于非等熵的情形,王泽军[7]证明了激波解的局部存在性.作为从Euler方程组分离出来的压差方程组(1),研究其活塞以不依赖于径向的速度扩张时激波解的局部存在性很有必要.
1 数学模型及主要结果
假设在初始时刻活塞位于原点,气体状态为u=0,p=p*.从t=0时刻开始,活塞的运动是柱对称的(只与t,r有关),则激波的位置及气体的速度也是柱对称的.为此作变换x=r cos θ,y=r sin θ,u=cos θ,v=sin θ,则方程组(1)变为(仍用u表示)
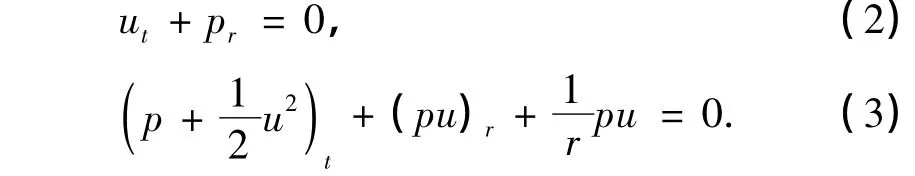
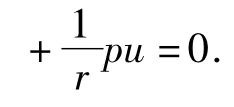
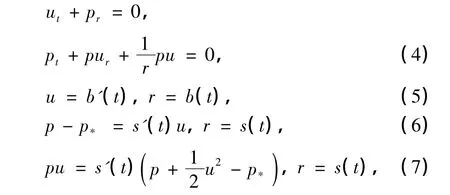
其中式(6)和(7)是Rankine-Hugoniot(R-H)条件.另外,在激波上有如下熵条件成立:
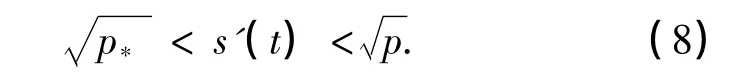

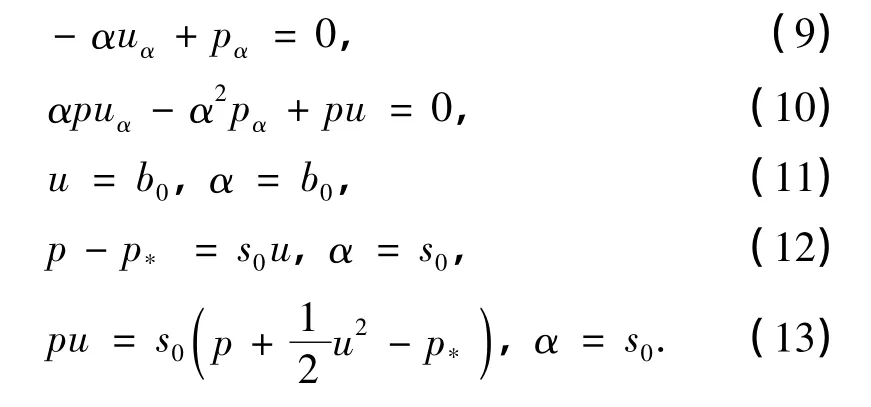
问题(9)~(13)激波解的存在唯一性可参见文献[3],可将其解称为未扰动解.本研究得出的主要结论如下.
定理1 假设b(t)∈C∞,b(0)=0,b'(0)=b0,且对2≤k≤K,b(k)(0)=0成立,其中K是一个适当大的正整数,则存在正常数T,使得当t≤T时,问题(2),(4)~(7)存在激波解.
2 近似解的构造

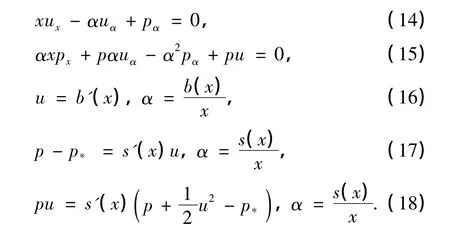
下面将构造问题(2),(4)~(7)的一个N阶近似解.仍记为(u,p,s),这里的N阶近似解指(u,p,s)在x=0附近满足问题(2),(4)~(7)的误差为O(xN),在第3节中,将以其作为迭代的首项.下面利用Taylor展开来构造近似解(u,p,s):
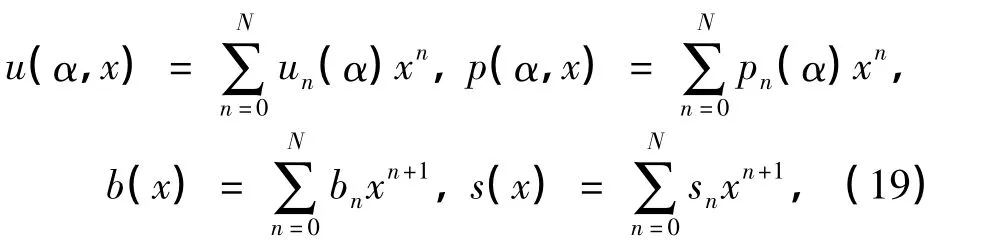
其中b(x)取的是定理1中b的Taylor展开的前N项.为确定上述(u,p,s)前N项的系数,将式(19)代入方程(14)及(15),并令所有xn(0≤n≤N)的系数为0,则有
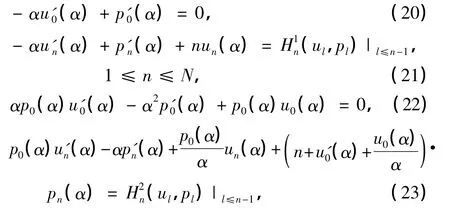
其中式(20)和(22)分别与式(9)和(10)具有相同的形式.对1≤n≤N,式(21)右端项(ul,pl)|l≤n-1表示所有仅包含ul和pl(l≤n-1)项的和,后面将不加解释地采用类似的符号.
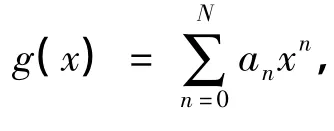
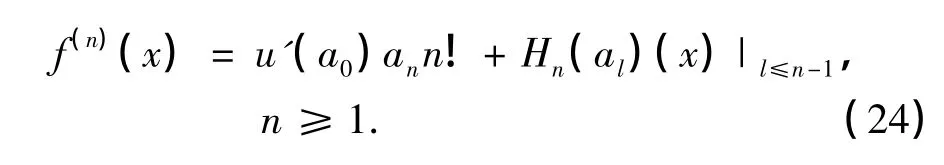

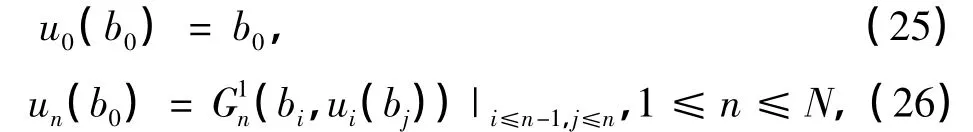
其中式(25)正是式(11).类似地,对于激波上的R-H条件,将式(19)代入方程(17)和(18)中,可得
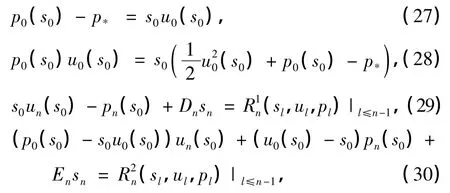
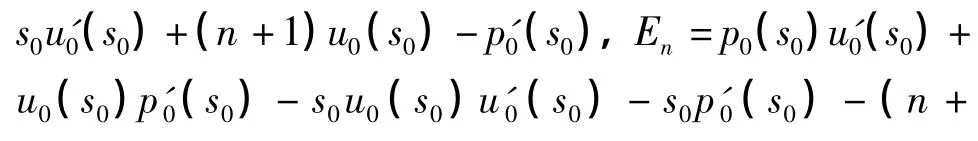
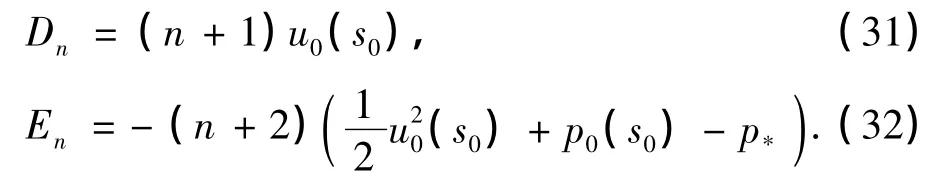
利用式(31)和(32),激波上的边界条件变为
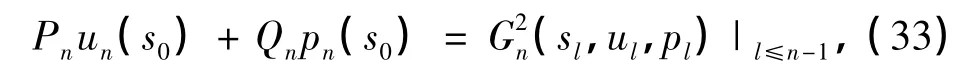
式中,
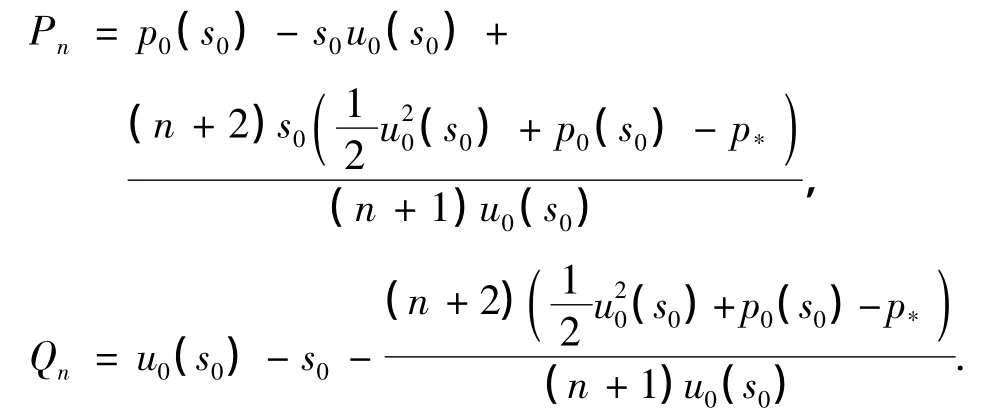
由式(20),(22),(25),(27),(28)可知,(u0(α),p0(α),s0)是问题(9)~(13)的解,则(un(α),pn(α))(1≤n≤N)满足方程(21),(23),(26),(33).由此,要构造问题(14)~(18)的N阶近似解(u(α,x),p(α,x),s(x)),只需对0≤n≤N求解一系列一阶线性常微分方程组的两点边值问题.当n= 0时,方程组由式(20),(22),(25),(27),(28)组成,它们等价于方程组(9)~(13);当1≤n≤N时,方程组由边值问题(21),(23),(26),(33)组成.当n=0时问题解的存在唯一性可由文献[3]得到,我们只需证明当n≥1时,问题(21),(23),(26),(33)存在唯一的经典解.
记φn(α)=(un(α),pn(α))T,则问题(21),(23),(26),(33)可写成如下形式:
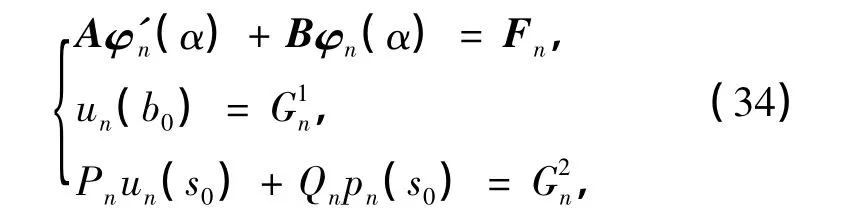
式中,
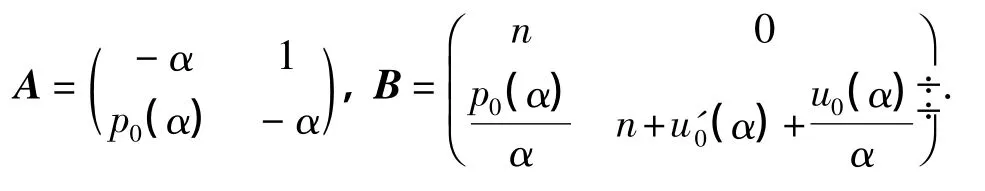
关于上述边值问题解的存在唯一性,有下面的命题.
命题1 当n充分大时,问题(34)存在唯一解.
证明 由常微分方程理论,问题(34)解的存在唯一性等价于相应的齐次问题
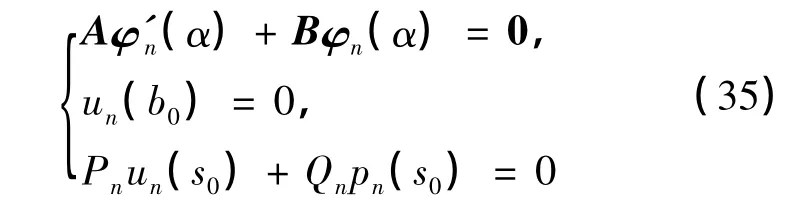
的0解的唯一性.用对角阵diag(p0(α),1)左乘式(35)中的第一式,可得
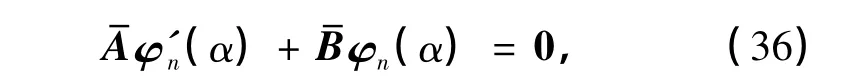
式中,
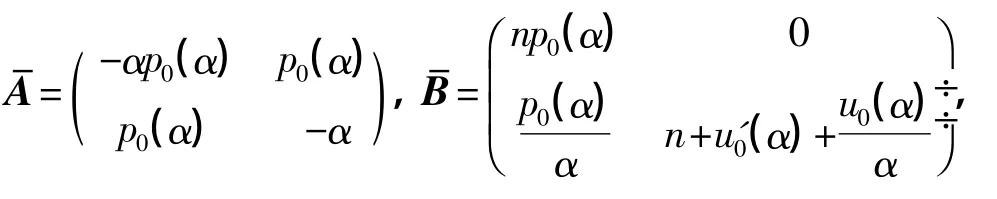
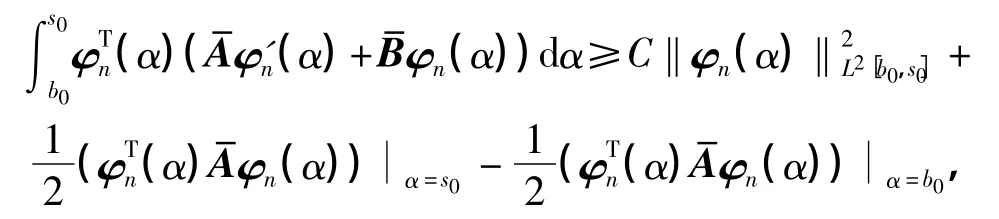
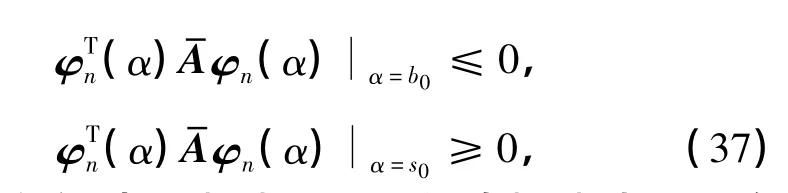
即得所要结论.由un(b0)=0,易得式(37)中第一个式子成立.
下证第二个式子,由式(33),只需证明-s0p0-.注意到,当n充分大时,该不等式等价于
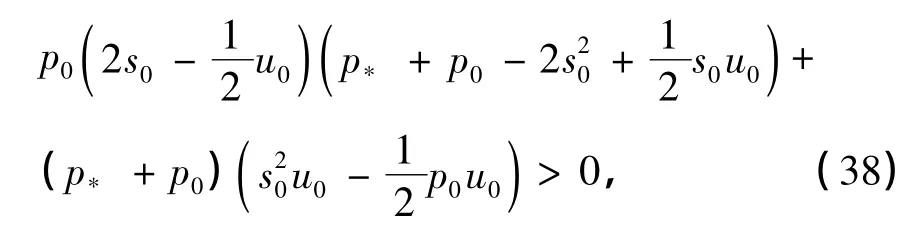
命题1保证了对于充分大的正整数K,当n≥K时,两点边值问题(34)存在唯一解.而当1≤n≤K时,由定理1的假设b(k)=0(2≤k≤K),未扰动解(u0(α),p0(α))已经满足式(14)~(18),这样就完成了近似解的构造,归为如下定理.
定理2 在定理1的假设下,对任意的正整数N,问题(2),(4)~(7)存在N阶近似解.
3 线性化及能量估计
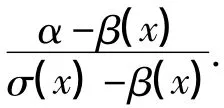
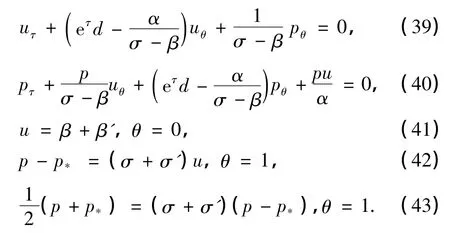
显然,问题(39)~(43)与问题(2),(4)~(7)等价,由第2节构造的近似解可知,问题(39)~(43)在τ=-∞附近的误差为O(eNτ),记为(u(0),p(0),σ(0)).
下面对问题(39)~(43)在近似解附近线性化,并选取适当的Hilbert空间来建立能量估计.
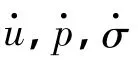
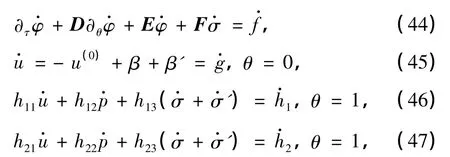
其中
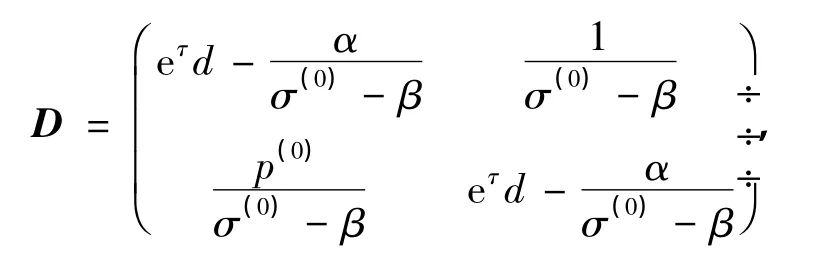
hij(1≤i≤2,1≤j≤3)是只依赖于u(0),p(0),σ(0)的系数,E,F是只依赖于(u(0),p(0),σ(0))的矩阵,,和是阶数为O(eNτ)的高阶小量.
类似于文献[5]中的证明,可得下面的能量估计.
定理3 设k是任意的正整数,T<∞,则存在η0>0,使得对任意的η>η0,问题(44)~(47)的解(,)满足如下的能量估计:
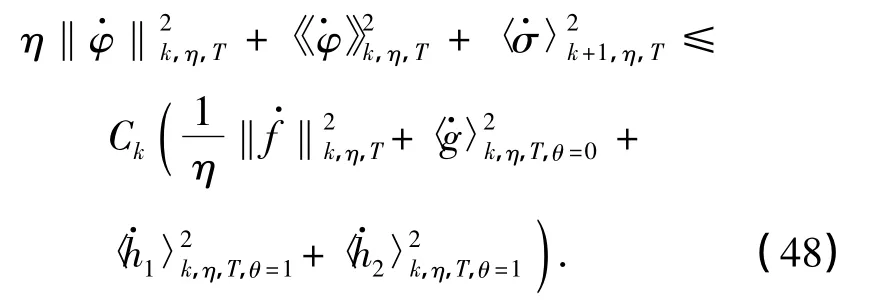
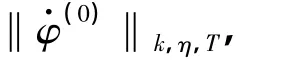
4 迭代过程与主要定理的证明
下面利用Newton迭代法的过程来证明定理1,从而得到问题(39)~(43)在近似解(φ(0),σ(0)) (φ=(u,p))附近解(φ,σ)的存在性.令
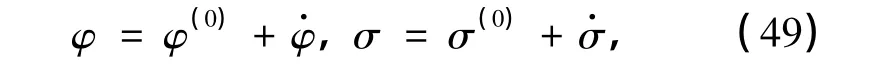
将式(49)代入到问题(39)~(43)中,可得
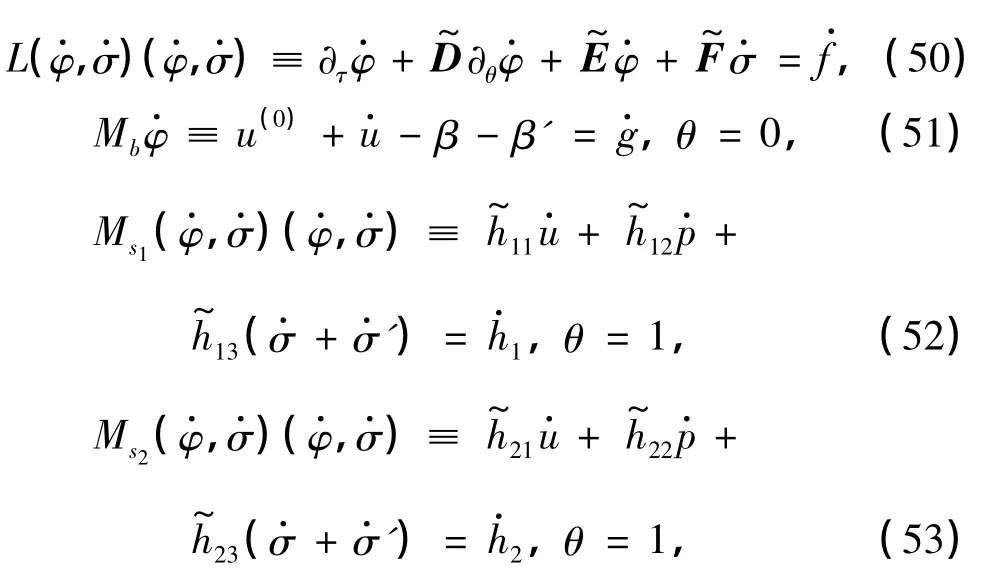
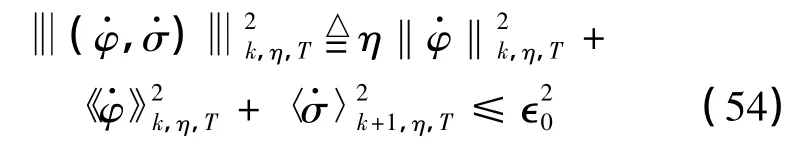
时,式(48)对k>2仍成立,并且式(48)中的系数Ck只依赖于ϵ0.
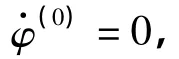
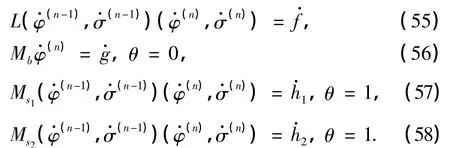
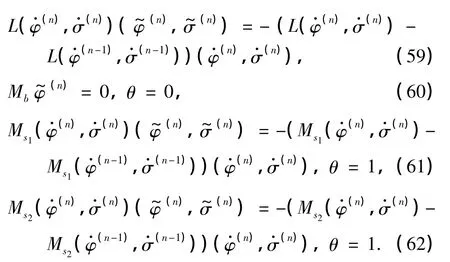
[1] LIJ Q,ZHANGT,YANGS L.The two-dimensional Riemann problem in gas dynamics[M].Boca Raton,FL:Crc Press,1998.
[2] WHITHAMG B.Linear and nonlinear waves[M].New York:Wiley,1974.
[3] CHENS X.A singular multi-dimensional piston problem in compressible flow[J].J Diff Eqns,2003,189(1):292-317.
[4] CHENG Q,CHENS X,WANGD H,et al.A multidimensional piston problem for the Euler equations for compressible flow[J].Dis Cont Dyn Sys,2005,13 (2):361-383.
[5] CHENS X,WANGZ J,ZHANGY Q.Global existence of shock front solutions for the axially symmetric piston problem for compressible fluids[J].Jour Hyper Diff Eqns,2004(1):51-84.
[6] CHENS X,WANGZ J,ZHANGY Q.Global existence of shock front solution to axially symmetric piston problem in compressible flow[J].Z Angew Math Phys,2008,59(3):434-456.
[7] WANGZ J.Local existence of the shock front solution to the axi-symmetrical piston problem in compressible flow[J].Acta Math Sinica,2004,20(4):589-604.
