多中继放大转发协同通信系统功率分配方法
2012-01-31杨洪兵郑国莘
武 卓, 杨洪兵, 郑国莘
(上海大学特种光纤与光接入网省部共建重点实验室,上海200072)
多输入多输出(multiple-input multiple-output,MIMO)[1]技术通过在系统的发送端和接收端配置多个天线,可以达到显著提升容量和分集复用增益的目的.然而,由于移动终端受尺寸、制造成本和设备复杂度等因素的制约,很难安装多个天线,因此,MIMO技术在移动终端中的应用受到了限制.协同通信的提出为MIMO技术的应用开辟了新的途径.协同通信的基本思想是,在多用户环境下,具有单天线的移动用户可以共享彼此的天线共同传输数据,以形成虚拟的MIMO系统.
功率分配技术一直是无线通信系统中对抗衰落和同频干扰的一项重要技术[2].合理的功率分配方案可以提高资源利用率,提升系统的容量和性能.协同通信系统的功率分配技术是在系统资源有限的前提下,根据不同的传输方式,确定某种准则.如先确定系统容量和接收端误码率,然后在约束条件下为源用户与中继用户分配功率,以最大限度地提高能量资源的利用率,进一步提高协同通信系统的容量,使网络发挥出最佳性能.
在多中继协同通信方面,文献[3]考虑了传统的多中继和机会中继2种协同方式,基于信道估计分别推导了放大转发协同方式的错误概率、中断概率和遍历容量的闭合表达式;文献[4]研究了多中继译码转发在Nakagami-m衰落信道中的性能,推导了译码转发系统中断概率的上限和下限;在LTE-A系统中,为了降低多个中继工作在同一频带和时隙中所带来的小区内干扰,文献[5]提出了一种低复杂度的贪婪中继选择算法;对于多中继系统的中继选择方案,文献[6]在译码转发协同通信系统中提出了一种低复杂度的中继选择算法,该算法的分集-复用权衡性能源于传统的协同方案;文献[7]在总发送功率恒定的条件下,提出了一种多中继放大转发通信系统的最佳功率分配方案,并推导了其理论表达式,但是没有分析中继个数对系统性能的影响;文献[8]针对多中继放大转发协同通信系统,提出了一种最小化误码率的功率分配方法,并且分析了中继数目对系统性能的影响.
现有的关于协同通信功率分配的研究大多基于一个简单的系统模型,算法复杂度较高,且需要预知全部信道状态信息,在实际应用中面临很大的困难.因此,本研究针对多中继放大转发协同通信系统,提出了一种新型的功率分配方法,以最小化发送功率为目标,将模拟退火(SA)算法应用于解决优化问题.
1 系统模型
多中继蜂窝协同通信系统上行链路的基本模型如图1所示.该系统由源用户S(source user),K个中继用户(协同用户)Rk(relay user)和目的节点D (destination)构成.在蜂窝移动通信上行链路中,目的节点为基站.
此处,采用放大转发(amplify-and-forward,AF)协同模式,将一次协同过程分为2个时隙:广播时隙和协同时隙.在广播时隙中,源用户以广播的形式向周围发送信息,这样,基站和处于接收范围内的部分用户可以收到其发送的信息;在协同时隙中,中继用户将接收到的来自源用户的信息以放大转发的方式发送到基站.在基站端,所有来自广播时隙和协同时隙的信息将采用最大比合并(maximum ratio combining,MRC)后进行进一步处理.在协同传输的2个时间相位中,假设源节点在2个正交的信道中传输信息,采用的接入方式为时分多址(time division multiple access,TDMA).
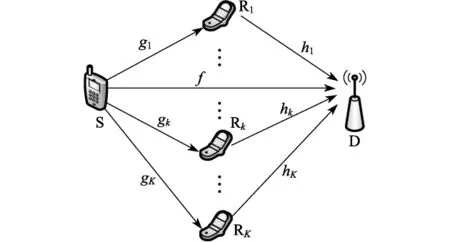
图1 多中继协同通信系统模型Fig.1 System modelofcooperativecommunication systems with multiple relays
这里同时假设源用户和各中继用户都是半双工的,也就是说,源用户和各中继用户不能同时发送和接收信息,调制方式采用二相相移键控(binary phase shift keying,BPSK).
在广播时隙中,各中继用户的接收信号ysrk和基站的接收信号ysd的表达式如下:
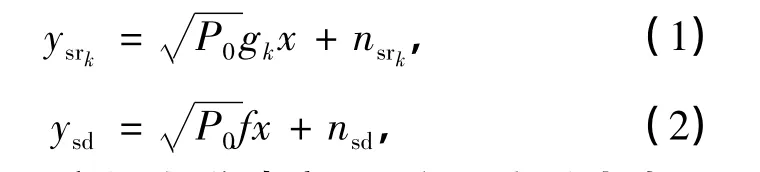
式中,P0为源用户的发送功率,gk和f分别代表源用户S到第k个中继用户Rk和源用户S到目的节点D(基站)之间的信道增益.x为源用户S的发送信号,nsrk和nsd均为加性高斯白噪声(additive white Gaussion noise,AWGN),分别代表S到Rk和S到D (基站)之间的信道噪声.
在协同时隙中,各中继用户将接收到的信号通过放大后转发到基站.基站端的接收信号yrkd可以表示为
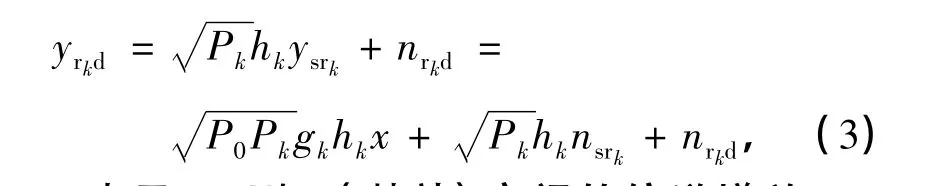
式中,hk表示Rk到D(基站)之间的信道增益,nrkd为对应信道中的噪声,这里假设其为AWGN,Pk为第k个中继用户的发送功率.
在基站端,为了使接收信噪比最大,采用MRC合并,接收信号的表达式如下:
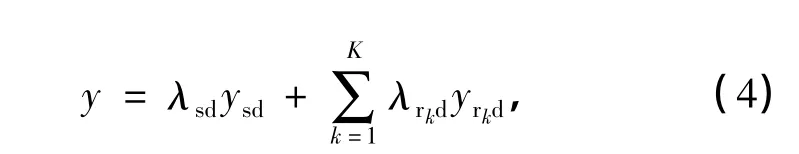
式中,λsd和λrkd分别为MRC合并中直接传输支路和协同传输支路的系数,其具体表达式为
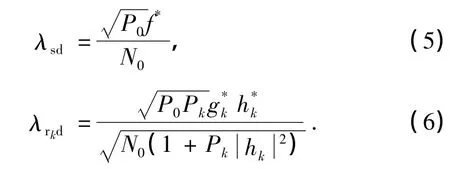
本研究提出一种最小化源用户和中继用户的总发送功率的功率分配方案 (power allocation proposed,PAp).如前所述,P0和Pk分别为源用户和第k个中继用户的发送功率.这里假设源用户和中继用户的总发送功率不恒定,且将Pk与P0之间的关系定义为

式中,αk为常数,且αk>0.因此,系统的总发送功率为

对于放大转发协同通信系统,经MRC合并后接收端的信噪比为
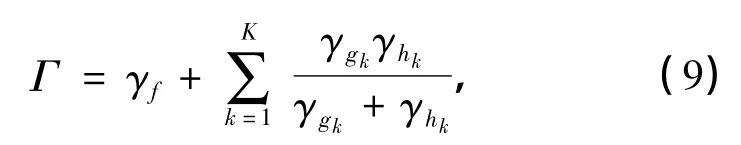
式中,γf,γgk和γhk分别为每个传输路径上的信噪比,具体计算表达式如下:
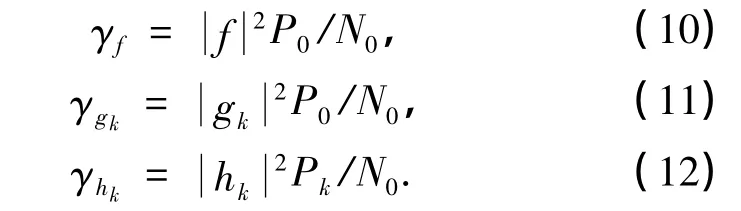
放大转发协同通信系统的误符号率[9]如下:
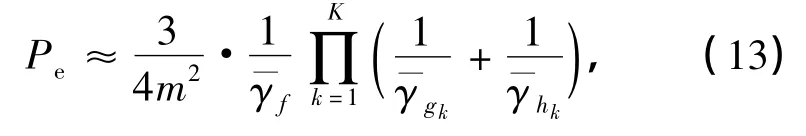
式中,m为常数,由调制方式决定.当采用BPSK调制时,m=2,式(13)即为系统的误码率表达式和分别为各传输支路的平均信噪比,是通过将式(10)~(12)中的和分别替换为F,Gk和Hk得到的.
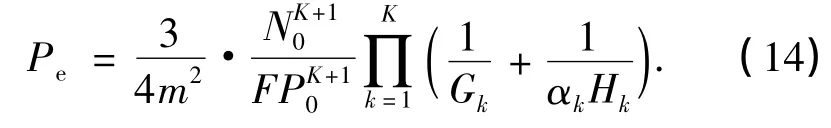
式(14)为误码率与源用户的发送功率之间的关系式,由此可以求得源用户的发送功率P0为
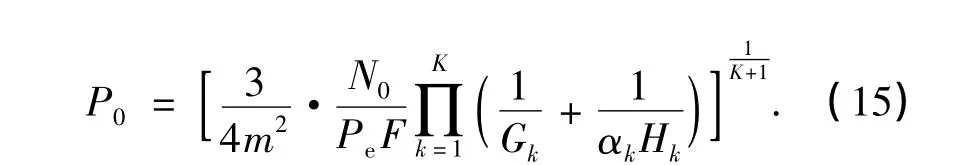
将式(15)代入式(8)中,可以得到源用户和各中继用户的总发送功率为
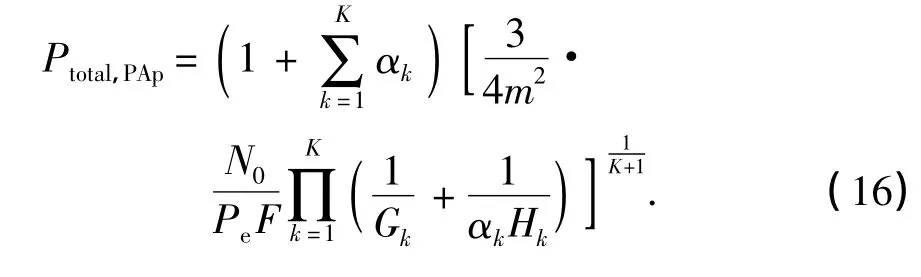
2 功率分配方案
本研究提出的功率分配方案以最小化发送功率为目的,其表达式(16)非常复杂,无法像文献[8]一样通过对该表达式直接计算求出功率分配因子.因此,需要通过一种有效且复杂度低的优化方案来解决此问题.
由于模拟退火算法[10-12]采用了 Metropolis算法[13],因此是一种全局寻优算法.Metropolis算法的优点是:过程解以一定的接受概率跳出局部极小,避免落入局部最小值点,然后在退火温度的控制下逐步找到最优解.如果没有Metropolis算法,就谈不上全局寻优,模拟退火算法最多只是一种局部算法的搜索,不能找到真正的最优解.
本研究提出的算法的目标函数如式(16)所示,其中Ptotal,PAp为α1,α2,…,αk的函数,而求其取最小值时的αk的值即为多元函数求极值问题,因此可以使用模拟退火算法来求解.
为求函数P(α)(α=[α1,α2,…,αK])的极值,模拟退火算法应用于本方案的步骤如下.
步骤一 初始化.随机产生α的初值点α0,估计最小值区间的下边界l和上边界u,选定最大迭代次数kmax>0,退火因子q>0(退火速度较快时,因子较大),以及相应的函数值浮动误差容许值εf.
步骤二 令α=α0,α0=α,P0=P(α0).P0和α0分别为将要求解的函数P(α)的最小值和取最小值时α的值.
步骤三 开始循环.从k=0循环到k=kmax.随机生成一个N×1的矢量β,其在[1,1]上服从均匀分布,β的大小与α相同.利用μ-1定理计算,可得
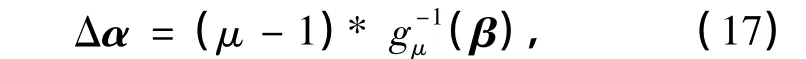
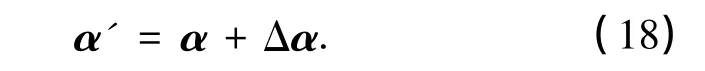
如果ΔP=P(α')-P(α)<0或者z<p= exp(-(k/kmax)qΔP/|P(α)|/εf),其中z是在区间[0,1]上服从均匀分布的随机数,则令 α=α',P(α)=P(α').
如果P(α)<P0,则令α0=α,P0=P(α0).
循环结束后,得到的P0和α0即为函数P(α)的最小值和取最小值时α的值.由此可以用迭代的方法求出本研究提出的功率分配问题.
若采用本研究提出的功率分配方案,则多中继放大转发协同通信系统的容量可以由下式求得:
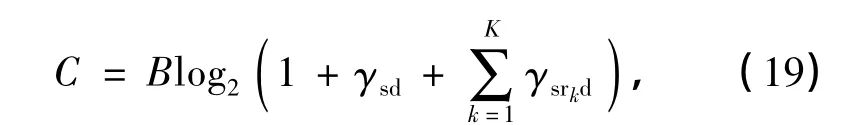
式中,B为系统带宽,γsrkd为中继链路的信噪比,
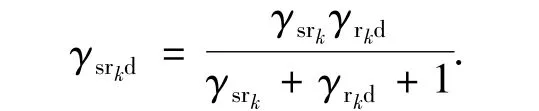
为了验证本功率分配方案的有效性,将其与消耗相等功率情况下的系统误码率性能作比较,并比较在同一目标误码率情况下本功率分配方案节省功率的情况.
在消耗相同功率的情况下,等功率分配方案(equal power allocation,EPA)消耗的总发送功率可以由下式计算得到:
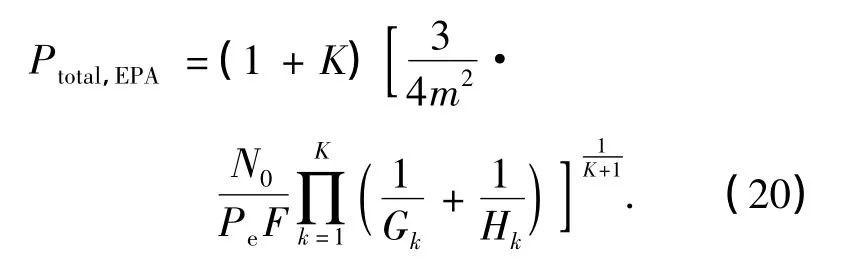
因此,将本研究提出的功率分配方案在同一目标误码率情况下消耗的功率与等功率分配方案相比较,定义η为节省的功率(百分比):
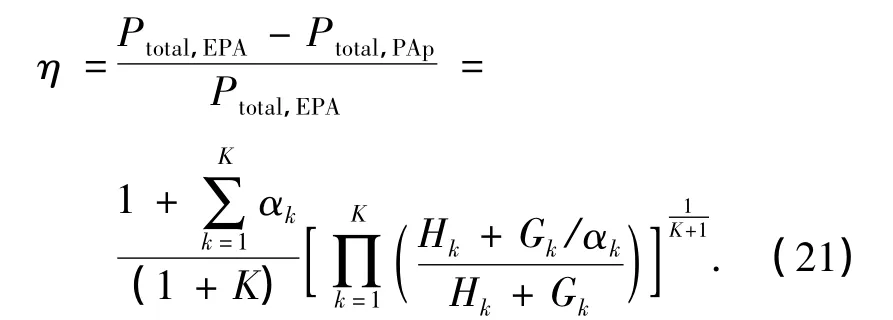
由式(21)可以看出,本研究提出的功率分配方案与消耗相同功率的等功率分配方案相比,所节省的功率(百分比)与源用户和各中继用户的发送功率、中继数目以及各中继链路的信道状态信息相关,而与目标误码率(bit error rate,BER)、噪声功率和直传链路的信道状态信息无关.
3 系统仿真与性能分析
下面将通过蒙特卡罗仿真图分析系统的误码率,以及系统容量受不同信道状态信息和中继个数的影响情况,其中将源用户的总发送功率限定为1.
图2为不同中继数目情况下,本研究提出的功率分配方案(PAp)与消耗相等功率的等功率分配方案(EPA)的误码率性能比较,图中实线为PAp的误码率曲线,虚线为EPA的误码率曲线.当中继数目为1,3,5,8时,采用PAp可以比EPA分别获得约0.5,1.0,2.2,3.0 dB的信噪比增益.
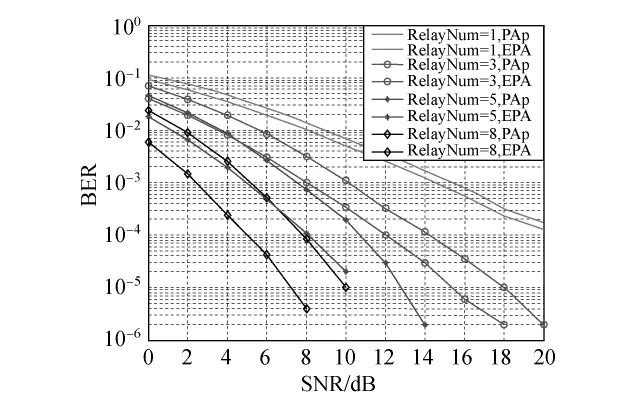
图2 不同中继数目情况下,PAp与EPA的误码率性能比较Fig.2 BER performance comparison of the PAp and EPA with different relay numbers
很显然,当中继数目增多时,所消耗的功率也越大.但是,实际通信系统中需要根据具体的情况选择合适的中继个数,而不会为了获得较大的信噪比增益而选择较多的中继参与协同,因为每个中继都是一个用户.为了保证协同通信的公平性,让其他用户参与协同是要付出代价的.如果选择的中继数目过多,虽然误码率性能提高了,但也许付出的代价更大了,这样通常就会“得不偿失”,而且消耗太多的功率,不利于用户电池的续航.
图3为在不同信噪比情况下,系统误码率随中继数目的增多而变化的情况.当信噪比较低时,系统误码率随中继数目的增多而缓慢下降;当信噪比较高时,系统误码率随中继数目的增多而下降较快.如果信道的信噪比较低,且要获得较好的传输可靠性,则可以选择相对较多的中继参与协同;如果信道的信噪比较高,则采用较少的中继就可以获得较高的传输可靠性.
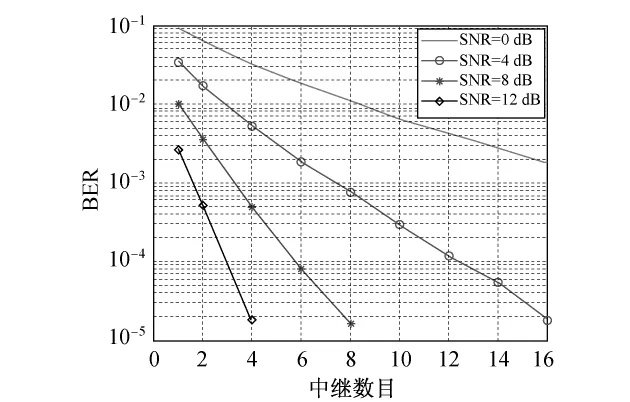
图3 不同信噪比情况下,PAp系统误码率随中继数目的变化关系Fig.3 BER performance of PAp versus different relay numbers under different SNR
图4为不同中继数目情况下,PAp与消耗相等功率的EPA的系统容量比较.在信噪比相同的情况下,当中继数目分别为1,3,5,8 dB时,采用PAp与EPA相比,系统容量可以分别提升0.1,0.2,0.3,0.5 bit/(s·Hz).当目标系统容量为3 bit/(s·Hz),中继数目为1,3,5,8时,采用PAp与EPA相比,可以分别获得约0.8,1.0,1.5,1.8 dB的信噪比增益.
由此可见,PAp无论是在系统可靠性能方面还是在有效性方面,都优于EPA.
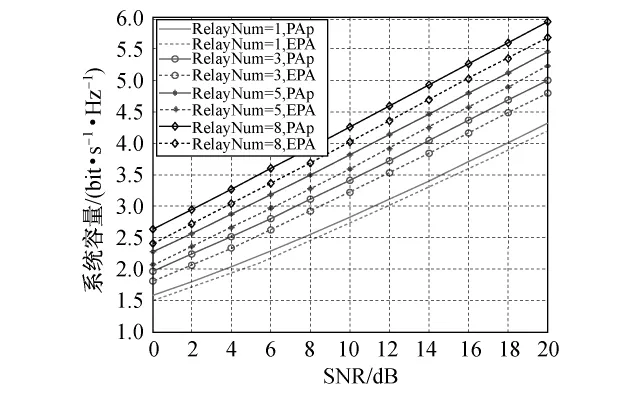
图4 不同中继数目情况下,PAp与EPA的系统容量比较Fig.4 System capacity comparison of the PAp and EPA with different relay numbers
图5为不同信噪比情况下,采用PAp的系统误码率随中继数目变化的关系.由图可见,系统容量随中继数目的增多而增大.当中继数目较少时,系统容量增大较快;当中继数目较多时,消耗的总功率增大了,但是系统容量增加缓慢,并趋于平缓.香农定理表明,系统的信道容量不会随着发送功率的增大而无限增大.
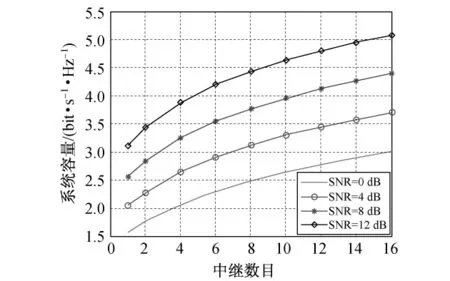
图5 不同信噪比情况下,PAp系统容量随中继数目的变化关系Fig.5 System capacity of PAp versus different relay numbers under different SNR
图6为当目标BER为10-3时,多中继放大转发系统采用PAp较EPA所能节省的功率.由图可知,节省的功率比与目标BER、信道噪声无关.所以,对于不同的目标BER和信噪比,所绘制出的功率节省图是相同的.
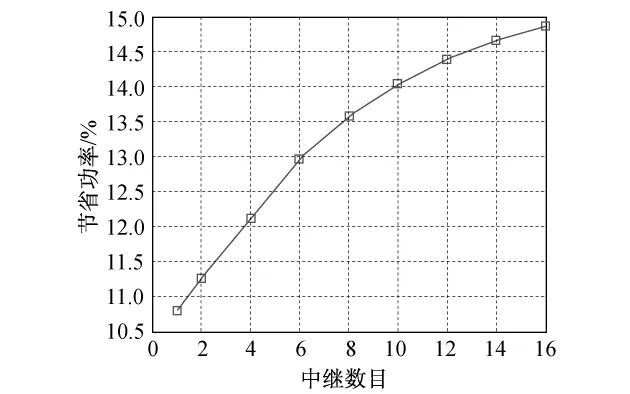
图6 给定目标BER情况下,采用PAp节省的功率(百分比)Fig.6 Power saved(%)with PAp under given BER
从图中可以看出,节省的功率百分比随中继数目的增多而增大.当使用1个中继时,可以节省约10.8%的功率;当使用16个中继时,可以节省约14.8%的功率.在实际通信系统中,由于用户的限制和所付代价的权衡,通常不会选择如此之多的中继参与协同.但采用此方法可以节省超过10%的功率,这对于移动通信终端的电池续航有非常重大的意义.
结合仿真图与相关分析可知,采用本研究提出的功率分配方案可以显著改善系统的误码率性能和系统容量.如果要获得足够好的系统可靠性能或者足够大的系统容量,可以通过增加中继数目的方法来实现.但是,增加中继数目会消耗更多的总发送功率,而且所付出的协同代价也可能会增大,所以,要在具体的信道环境中,选择合适的中继数目.采用本研究提出的功率分配方案,可以降低系统的误码率性能,提升系统容量,为用户节省更多的功率,延长终端电池的使用寿命.
由第2节的模拟退火算法步骤可以看出,该算法的复杂度主要依赖于模拟退火因子q和最大迭代次数kmax,这里的仿真参数设为q=0.8,kmax=800.同时,该算法的精确度较高,而且复杂度相对较低.与其他优化算法相比,模拟退火算法由于受初值影响较小,因此在精确度上要优于遗传算法(genetic algorithms,GA)[14];而粒子群优化(particle swarm optimization,PSO)算法[15]虽然精确度高,但是算法复杂度远高于模拟退火算法.
4 结束语
本研究针对多中继放大转发协同通信系统,提出了一种新的功率分配方法.该方法以最小化发送功率为目标,应用模拟退火算法解决了优化的问题.仿真结果表明,本研究提出的功率分配方案在系统可靠性和容量方面比等功率分配方案有明显的增益.在给定目标误码率的情况下,采用本方案可以节省超过10%的功率,这对于提高移动通信终端的能量利用率是非常有意义的.另外,所采用的模拟退火算法的精确度高于遗传算法,且算法复杂度低于PSO算法,是一种折衷的算法.
[1] FOSCHINIG J,GANSM J.On limits of wireless communications in a fading environment when using multiple antennas[J].Wireless Personal Communications,1998,6:311-335.
[2] NOSTRATINIA A, HUNTER T E, HEDAYATA.Cooperative communications in wireless networks[J].IEEE Commun,2004,42(10):74-80.
[3] AMINO,IKKIS S,UYSALM.On the performance analysis of multi-relay cooperative diversity systems with channel estimation errors[J].IEEE Transactions on Vehicular Technology,2011,60(5):2050-2059.
[4] HUANGS Q,CHENH H,LEEM Y.Performance bounds of multi-relay decode-and-forward cooperative networks over Nakagami-m fading channels[C]∥2011 IEEE InternationalConference on Communications.2011:1-5.
[5] HUY L,QIUL.A novel multiple relay selection strategy for LTE-advanced relaysystems[C]∥ Vehicular Technology Conference(VTC Spring).2011:1-5.
[6] ZHANGS Q,LAUV K N.Multi-relay selection design and analysis for multi-stream cooperative communications[J].IEEE Transactions on Wireless Communications,2011,10(4):1082-1089.
[7] LINF,LIUX M,LUOT,et al.Optimal power allocation to minimize SER for multi-node amplify-andforward cooperative communication systems[J].Journal of China Universities of Posts and Telecommunications,2008,15(4):14-18.
[8] WUZ,YANGH B.Power allocation of cooperative amplify-and-forward communications with multiple relays[J].JournalofChina UniversitiesofPostsand Telecommunications,2011,18(4):65-69.
[9] RIBEIROA,CAIX D,GIANNAKISG B.Symbol error probabilities for general cooperative links[C]∥ 2004 IEEE InternationalConference on Communications.2004:3369-3373.
[10] BRYAN K, CUNNINGHAM P, BOLSHAKOVA N.Application of simulated annealing to the biclustering of gene expression data[J].IEEE Transactionson Information Technology in Biomedicine,2006,10(3):519-525.
[11] TURGUTD,TURGUTB,ELMASRIR,et al.Optimizing clustering algorithm in mobile ad-hoc networks using simulated annealing[C]∥ Wireless Communications and Networking Conference(WCNC 2003).2003:1492-1497.
[12] MIRM.Application of simulated annealing to clusterboundarysearch algorithm formacrocellplacement optimization[C]∥ 2010 International Conference on Computer and Communication Engineering(ICCCE).2010:1-4.
[13] 陈华根,吴健生,王家林,等.模拟退火算法机理研究[J].同济大学学报:自然科学版,2004,32(6):802-805.
[14] HIROYASUT,MIKIM,IWAHASHIT,et al.Dual individual distributed genetic algorithm for minimizing the energy ofprotein tertiary structure[C]∥Proceedings of the Society of Instrument and Control Engineers(SICE).2003:2756-2761.
[15] ALIF A,SELVANK T.A study of PSO and its variants in respect of microstrip antenna feed point optimization[C]∥ Asia Pacific Microwave Conference(APMC 2009).2009:1817-1820.
