基于一种新的γ-扩张凹极小化问题的割平面算法
2012-01-31刘林娜杨永建
刘林娜, 杨永建, 余 峰
(上海大学理学院,上海200444)
近年来,人们已经较为深入地研究了凸规划问题,并且给出的方法大多非常有效[1].但是,对于在生活中有着很强实际应用背景的一些问题,如金融经济[2-3]、工程设计和非线性系统的鲁棒稳定性分析[4]等却只能表示为非凸规划问题.虽然非凸二次规划问题是困难的多极值全局优化问题,但仍有不少学者在这方面取得了一定的进展[5-8].本工作主要研究一类特殊的非凸二次规划问题——凹极小化问题.凹极小化问题是一种比较常见的多极值优化问题,在全局优化领域有着重要的应用.许多类型的优化问题,如0-1整数规划问题、双线性规划问题、互补问题和某些乘积问题等都可以转化为等价的凹极小化问题.如
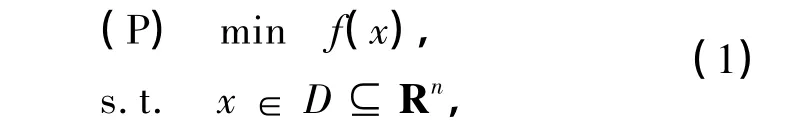
式中,f(x)∶Rn→R在非空集合D上是凹的,D为Rn中非空凸集(假设D为多面体).事实上,如果问题(P)的最优值不是∝,则一定可以在D的顶点处找到一点,使f(x)在该点取到最优值,即凹函数在多胞形上的全局极小值一定是在多胞形的某个顶点取到,并称该性质为极点最优性.进一步来说,当可行域为紧凸集时,凹函数的极点最优性仍然成立.本工作先作以下2个假设.
假设1 凹函数f(x):D→R可延拓到F(x):Rn→R,且F(x)为可微函数.
假设2 凸集D为多胞形,且有非退化的顶点,即int D≠Ø.
下面对以上假设作进一步说明.
命题1 令D⊆Rn是凸的,int D≠Ø,f:D→R
在D上是凹函数,并且是连续的.假设‖Δf(x)‖在集合DΔ={x∈D:f(x)在x点是可微的}上是有界的,其中 Δf表示 f的梯度,‖·‖为欧几里得范数,则
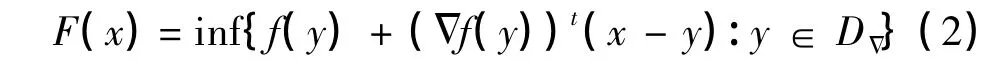
在Rn上是凹的,且在D上,有F(x)=f(x).
证明 对任意的y∈DΔ,令
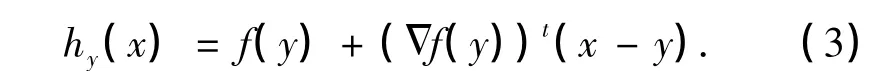
对于每个y,hy是仿射的,F(x)是仿射函数的下确界,所以F(x)在Rn上是凹的.对于所有的x,y∈DΔ,hy(x)≥f(x).在DΔ上,有hx(x)=f(x),因此,F(x)=f(x).由于DΔ在int D内是稠密的,根据f在D上的连续性可知,在D上有F(x)=f(x).
假设D是多胞形,且int D≠Ø,显然等价于dim D=n.若dim D=d<n,则可以在一个包含D的d维空间内进行讨论.
割平面的概念是由Gomory在1958年首先提出用来构造整数规划的算法.Gomory割平面是通过不断求解其线性规划松弛形式,构造合适的割平面,从而去掉松弛形式的非整数解,最终找到一个整数向量的最优解.该算法能够保证整数规划在有限步内求得最优解.后来,Tuy[8]又提出了一种求解凹极小化问题的割平面,其中心思想是:基于以上2条假设,易求得可行域D的一些可行点,通过传统的线性规划算法(如单纯形方法)可以找到D的一个顶点v1.由f(x)的可微性可知,D的发自v1的边方向d,由此可找到满足dtΔf(v1)<0的方向d.对于v1的邻点v2=v1+ λd,可根据f(x)的凹性,即f(v2)≤f(v1)+(v2-v1)t· Δf(v1)(由于(v2-v1)tΔf(v1)<0,且f(v2)<f(v1)),通过转轴方法或者标准的非线性规划的局部算法,总可以找到f(x)在D上的一个局部极小点x0.令γ=f(x0)≥min{f(x):x∈D},由此构造超平面H,一般称之为割或者割平面,使得对于所有的x∈D∩H-,有f(x)≥γ,即试图通过割掉一部分可行域,来保证该部分上的目标函数值不小于f(x0).若可行域剩下的部分不为空集,则可用同样的方法应用到剩余部分.
1 变上限积分函数方法
考虑变上限积分函数[9]

式中,x*为f(x)在可行域D上的局部极小点,d是一个已知方向,r=f(x*)是局部极小值.若f(x)为强制函数,则F(x*,t)也为强制函数.下面给出F(x*,t)的一些性质.
定理1 设x*是f(x)的一个局部极小点,若f(x)在以 x*为起点,以 d为方向的射线上恒有f(x)≥r,即对于任意的s≥0,有f(x*+sd)≥r,那么函数F(x*,t)是一个关于t的增函数.
证明 对函数F(x*,t)求导,可得
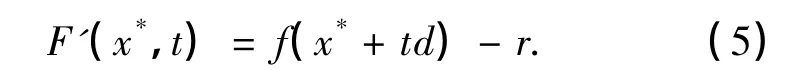
由条件f(x)≥r可知,F'(x*,t)≥0,故F(x*,t)是关于t的增函数.
定理2 设x*是f(x)的一个局部极小点,若f(x)在以x*为起点,以d为方向的射线上存在函数值小于r的点x,那么在该射线上一定存在一点x0,使得f(x0)=r,并使得对应的t0是函数F(x*,t)的局部极大点,其中x0=x*+t0d.
证明 假设在射线上存在一点x',使得f(x')<r.因为f(x)连续,由介值性定理可知,在该射线上一定存在一点x0,使得
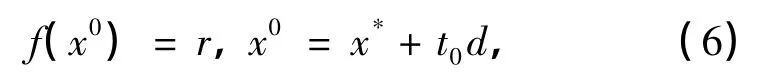
并且存在t0的一个邻域(t0-δ,t0+δ)(δ>0),使得当t∈(t0-δ,t0]时,f(x*+td)≥r;当t∈(t0,t0+δ)时,f(x*+td)≤r.
任取t∈(t0-δ,t0],有
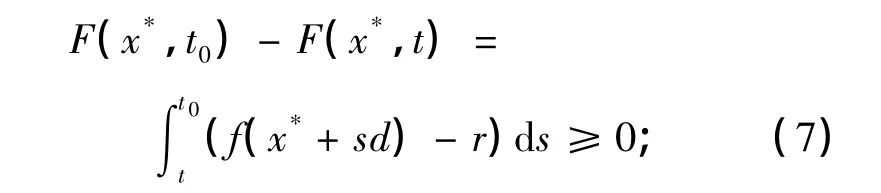
任取t∈(t0,t0+δ),有
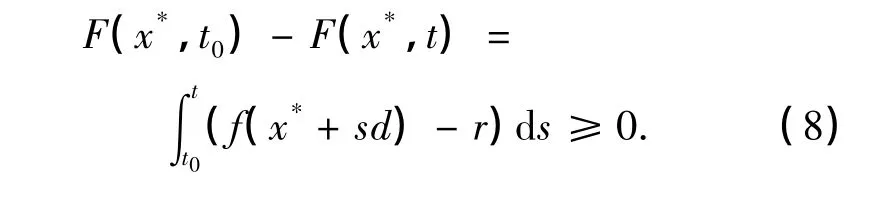
故t0为函数F(x*,t)的局部极大点.
定理3 设x*是f(x)的一个局部极小点,对于某个方向d,若t*是函数F(x*,t)的一个平稳点,则有f(x*+t*d)=r.
证明 对函数F(x*,t)求导,得到
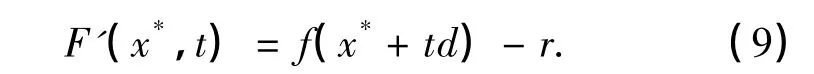
由于t*是F(x*,t)的稳定点,则有
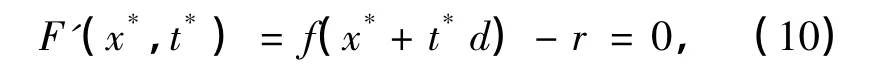
即有f(x*+t*d)=r.
下面,考虑问题
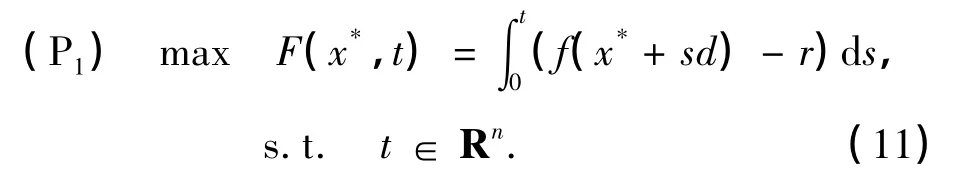
可以利用局部算法来求解问题(P1),这里采用Newton算法,算法步骤如下.
步骤1 初始化.给定初始点tk,误差控制ϵ>0,记k=0.
步骤4 迭代改进.通过线搜索确定步长参数αk,令tk+1=tk+αkek,置k+1→k,转步骤2.算法终止.
Newton算法比最速下降法的收敛速度要快,固定步长αk=1,则迭代产生的序列{tk}是收敛于点t*的,且为二阶收敛.通过Newton算法可以找到问题(P1)的极大点t*.
2 割平面算法
首先,假设凹极小化问题(P)的可行域
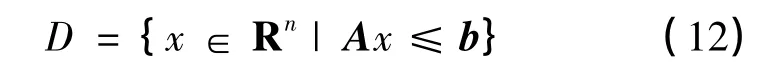
是非空闭凸集,式中,A为m×n阶矩阵,b为欧式空间的n维向量.通过传统的线性规划(如单纯形法)可求出 f在 D上的一个局部极小点 x0.显然有f(x0)≥min{f(x):x∈D},令γ=f(x0),我们感兴趣的区域为D(γ)=D∩{x∈Rn|f(x)<γ}.在求解凹极小化问题的算法中,首要任务是在以x为起点,d为方向的射线ρ(x,d)={y:y=x+td,t≥0}上找到最长的线段[x,x+t*d],使得对所有的y∈[x,x+ t*d],有f(x)≥γ.特别地,γ是在极小化过程中的某一阶段得到的最佳目标函数值.在区间[x,x+t*d]中,不会有比当前局部最优值更佳的最优值.若f(x)为严格凹的,且上水平集L(f(x);γ)={x:f(x)≥γ}有界,则y=x+t*d是射线ρ(x,d)与L(f(x);γ)的边界的交.若L(f(x);γ)沿d无界,则t*=+∝,即在整个射线ρ(x,d)上有f(y)≥γ,这时一般取t*=t1,其中t1为充分大的正数.
下面给出γ-扩张的定义.
定义1 令f:Rn→R是凹函数,x∈Rn,γ是满足γ≤f(x)的实数,并且t1>0充分大.称点y∈Rn为x沿方向d∈Rn�(相对于f)的γ-扩张,即y=x+ t*d,其中t*=min{t1;sup{t:f(x+td)≥γ}}.
由于f的凹性,其上方水平集L(f(x);γ)为凸集,所以可采用线搜索、托架-二分技术等来确定x沿方向d的γ-扩张.但是,在求解过程中,线搜索的收敛速度比较慢,且收敛效果不好;托架-二分技术实质上也是线搜索中对分法的扩展,具有线搜索的缺点.关于γ-扩张可以通过求解变上限积分函数的极大值来确定.
2.1 有效割
定义2 若D(γ)⊆{x∈D|p(x)≥0}成立,则称p(x)为(f,D)的一个γ-有效割.
可以看出,γ-有效割没有割去任何一个满足f(x)<γ的可行点.若对于f(z)>γ的可行点z∈D,希望找到一个有效割,使得它能将点z与D(γ)分离,即p(z)<0,对任意的x∈D(γ),p(x)≥0.显然,D的有效割并不是唯一的,甚至有无穷多个.
定义3 若(f,D)的一个γ-有效割p1(x)≥0去掉的D∩L(f(x);γ)的部分比另一个 γ-有效割p2(x)≥0多,则称p1(x)≥0强于p2(x)≥0.
显然,我们希望得到一个最强的有效割,即为凹性割.由问题(P)的可行域D出发,可以找到D的一个顶点v.以v为顶点,以线性无关的向量组d1,d2,…,dn为边方向,可得到一个凸的多面锥 K= K(v;d1,d2,…,dn),此时,令γ=f(v).
令ρ(v,di)={v+tdi|t≥0}与L(f(x);γ)边界的交点为

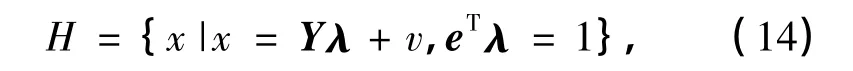
等价表示为
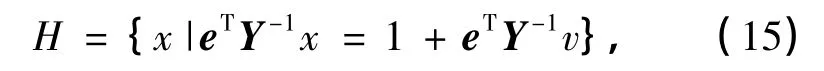
式中,e=(1,1,…,1)T∈Rn,λ=(λ1,λ2,…,λn)T,Y=(y1-v,y2-v,…,yn-v)是n阶矩阵,顶点v∈H-,H-={x|eTY-1x≤1+eTY-1v}.
定义4 称线性割eTY-1(x-v)≥1为(f,D)的一个凹性-有效割,简称凹性割.
定理4 对于所有的x∈D∩H-,有f(x)≥γ.
证明 由于D⊆K,故D∩H-包含在单纯形S=[v,y1,y2,…,yn]中.凹函数f在S上的最小值可在S的一个顶点上取得,因此,有
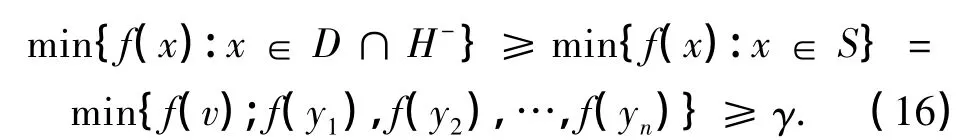
上面的定理说明,通过割平面式(16),从D中割去D∩H-,并不会损失任何目标函数值比γ更佳的可行点,当D⊆H-时,则有γ=min{f(x):x∈D}.
2.2 凹极小化问题的割平面算法
求解凹极小化问题的割平面算法步骤如下.
步骤1 置S←D.
步骤2 求解问题(P)的可行域的一个非退化顶点v,即v∈V(S),V(S)是多胞形S的顶点集.找到n个线性无关的方向d1,d2,…,dn,以v为顶点沿方向 d1,d2,…,dn,构造凸多面锥 K=K(v;d1,d2,…,dn),令上界γ=f(v).
步骤3 构造点v,相对于f沿方向d的γ-扩张,通过前述Newton算法求解变上限积分函数
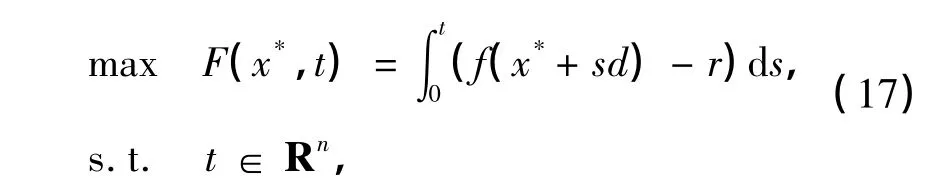
步骤5 若S⊂H-,算法终止,v就是所求的全局极小点.否则,转步骤6.
步骤6 置S←S∩H+,转步骤2.
下面对以上算法作几点说明:步骤2可以用线性规划的单纯形方法来求解,当v是非退化顶点时,可以找到相邻的n个邻点vi,i=1,2,…,n,故可取di=vi-v,i=1,2,…,n,从而构造一个凸多面锥;步骤3可以用变上限积分函数法来求解;步骤4中的正数M在不同问题中的取值有差别,主要取决于所求问题的数据.
2.3 割平面算法的收敛性
凹性割算法的基本原理是先选择D的一个子集作为目标集合S,比如S=D(γ).然后,确定一个凹性有效割⊇S.若对于k=1,2,…,可找到点xk∈D∩,且xk∈S,则搜索终止;否则,对于D的某个覆盖{Dk,j:j=1,2,…,Nk},构造Nk个凹性割,使得对应的集合(j=1,2,…,Nk)满足
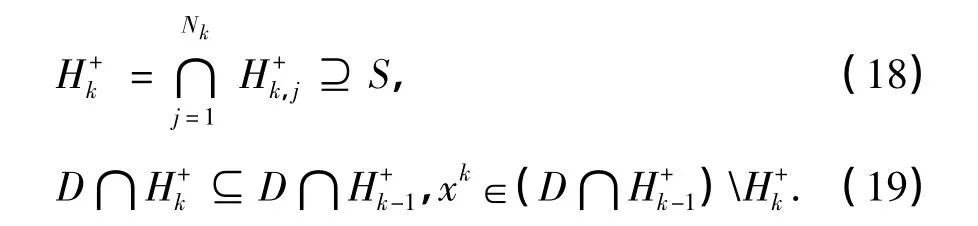
最后,确定新的点xk+1∈D∩,继续搜索.
凹性割算法的搜索过程有2种结果:一是存在某个k,有xk∈S;二是得到一个无穷序列{xk}.称前者为凹性割算法的有限收敛,后者为凹性割算法的无限收敛.
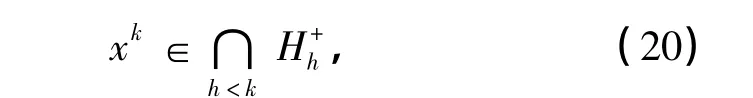
则点xk与集合的距离

证明 反证法.
假设结论不成立,则存在ϵ>0和点列{kq},对于任意的q=1,2,…,使得d(xkq)≥ϵ.由于{xk}是有界的,不妨设{xkq}是收敛的,对于充分大的u,v,‖xku-xkv‖≤ϵ成立.由式(21)可知,对于所有的u>v,有xku∈.故有
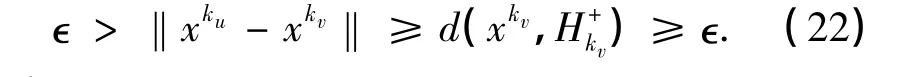
显然这是矛盾的,所以假设不成立.
定理6 在凹性割算法中,假设集合
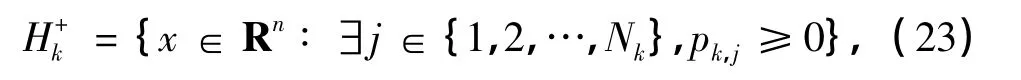
并且有界点列{xk}满足
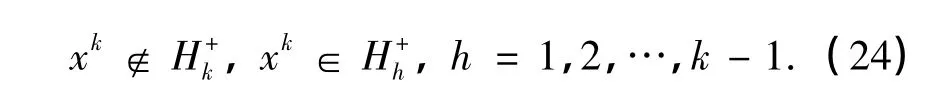
若存在ϵ>0,使得d(xk,∂)≥ϵ,其中∂是的边界,则凹性割算法是有限收敛的.
证明 根据式(24)可知,式(21)成立.由于d(xk,)=d(xk,∂,所以对于任意的k,d(xk,≥ϵ.由定理5可知,凹性割算法生成的序列{xk}是有限的,即凹性割算法是有限收敛的.
3 数值试验
下面利用凹规划问题来证明本工作提出的新算法是有效可行的.
例 min{f(x)=xtQx+2ptx:Ax≤b,x≥0},其中
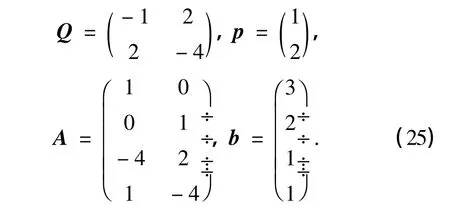
迭代1 容易找到初始多胞形的一个顶点v1= (0,0),其邻接的2个顶点分别为u1,1=(1.0,0),u1,2=(0,0.5);得到当前最佳可行点x1=(0,0),以及当前最佳目标函数值γ1=f(x1)=0,则x1沿方向u1,1-x1,u1,2-x1的γ-扩张分别为y1,1=(2.0,0),y1,2=(0,1.0),可得到凹性割0.5x1+x2≥1.
迭代2 通过迭代1割去0.5x1+x2≥1这一部分后的新多胞形的一个顶点v2=(0.2,0.9),其邻接的2个顶点分别为 u2,1=(1.67,0.17),u2,2= (0.75,2.0);当前的最佳可行点是 x2=(0.75,2.0),当前最佳目标函数值γ2=f(x2)=-1.06,则x2沿方向 v2-x2,u2,1-x2的 γ-扩张分别为 y2,1= (2.13,-0.06),y2,2=(0.75,2.0),可得到凹性割0.78x1+0.52x2≥1.62.
经过4次迭代,算法终止,并且产生 x*= (0.75,2.0)对应的最优解f(x*)=-1.06.在求解γ-扩张时,采用本工作介绍的Newton算法很容易实现.数值试验结果表明,本工作所提出的算法可以加速收敛,是可行有效的,计算的结果与实际情况相符.
[1] 高岳林,叶留青,张连生.带有二次约束二次规划问题的分枝定界方法[J].工程数学学报,2003,14(2):82-86.
[2] KONNOH,WIJAYANAYAKEA.Portfolio optimization problem under concave transaction costs and minimal transaction unit constraints[J].Math Prog Ser B,2001,89(2):233-250.
[3] BAJIROVA M,RUBUNOVA M.Global optimization of marginal functions with applications to economic equilibrium[J].Journal of Global Optimization,2001,20(3/4):215-317.
[4] 吴慧卓,段东东,张可村.一种新的求解带有非凸二次约束的非凸二次规划问题的加速全局优化方法[J].工程数学学报,2009,26(1):75-84.
[5] FALKJ E,CARDONAE L.The surgical separation of sets[J].Journal of Global Optimization,1997,11(4):433-462.
[6] HORSTR,THOAIN V.Utility function programs and optimization over the efficient set in mulitiple-objective decision making[J].Journal of Optimization Theory and Applications,1997,117(2):605-631.
[7] MOHDI B,YOSZAD.Constraint exploration method for quadratic programming problem[J].Applied Mathematics and Computation,2000,112(2/3):161-170.
[8] TUYH.Concave programming under linear constraints[J].Journal Doklady Akademii Nauk SSSR,1964,159 (1):32-35.
[9] YANGY J,BAIF S.An integral function and vector sequence method for unconstrained global optimization[J].Journal of Global Optimization,2011,50(2):293-311.
