考虑中继时延的协作中继选择方法
2018-12-19周忠瑶
何 杰 肖 琨 周忠瑶
(广西师范大学电子工程学院,桂林,541004)
引 言
在一个协作通信网络中,信源通过一系列协作中继节点的辅助把消息传送给信宿。协作通信利用空间分集技术,克服无线信道衰落,不仅能提高无线系统的通信质量,还能扩大通信系统的覆盖范围。这其中,性能优良的中继选择方法对于实现这些目标显得尤为重要。
目前文献中已经有一些中继选择方法的研究,这些中继选择方法各有特点。文献[1-5]提出了根据链路信噪比选取中继节点的方法,如机会中继选择(Opportunistic relay selection, ORS),最大-最大中继选择(Max-max relay selection, MMRS),最大链路中继选择(Max-link relay selection, MLRS)等,这些选择方法都是以链路信噪比作为唯一选择准则,选出信噪比满足某一表达式条件的中继节点作为转发节点。文献[6-8]则以容量最大化为准则选取中继节点,将信道容量作为中继选择的唯一依据。以上中继选择方法忽略了实际系统中继选择需要考虑的因素,如节点的缓存器大小等。而文献[9-12]以中断概率最小化作为准则设计中继选择方法,依赖于系统的中断概率计算,增加了中继选择算法的计算复杂度。中继选择方法还可以和功率分配结合考虑,设计以功耗最小化为准则的中继选择方法[13-18]。但是,这些研究工作都没有考虑数据业务在中继节点处可能存在的时延,而对于数据业务来说,这一点是至关重要的。文献[19]提出了一种考虑时延的中继选择方法,把时延作为中继选择考虑的主要因素, 忽略了信道容量和业务时延的平衡关系,而且难以进行数学分析,存在较大的局限性。
本文将中继时延和信道状态相结合,提出了一种新的旨在减小中继时延的中继选择策略,通过对中继链路的信噪比加权,在中继时延越大的中继链路上对信噪比施加越大的影响,使得在相同信噪比的情况下,中继时延越大的中继链路的加权信噪比的值越大,从而被选中用于数据转发的概率越高,有效降低数据业务的中继时延,具有积极的科学意义和应用价值。
1 中继选择模型
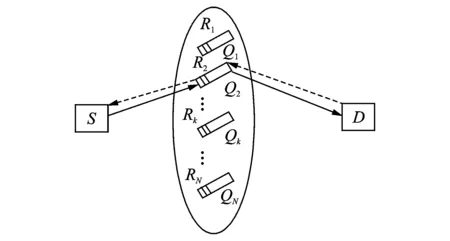
图1 中继选择模型Fig.1 Relay selection model
本文提出的中继选择模型如图1所示,由一个源节点S、一个目的节点D和N个译码转发(Decode-and-forward, DF)中继节点Ri(i=1,2,…,N)组成,这些中继节点构成了中继节点集合Srelay并具有一定存储能力,其存储空间大小为Qi(i=1,2,…,N)。协作传输分为两个时隙,在第一个时隙,源节点广播数据,中继节点和目的节点接收,在第二个时隙,在源节点到中继节点链路和中继节点到目的节点链路的信噪比同时大于中断门限γth的l个中继节点构成的候选中继集合Ξl(Ξl⊆Srelay)中,根据中继选择方法选取一个中继节点转发源节点S的数据到目的节点D。图中的虚线为反馈信道,在中继选择过程中,中继节点和目的节点通过反馈信道把用于中继选择的相关参数反馈给源节点。
为简化分析但不失一般性,采用瑞利衰落信道,假设源节点与目的节点之间不存在有效的直接路径[2-3]。定义源节点S到中继节点Ri之间链路(记为S-Ri链路)的信噪比为γSRi,中继节点Ri到目的节点D之间链路(以下记为Ri-D链路)的信噪比为γRiD,则γSRi和γRiD的概率密度函数(Probability density function, PDF)可以分别表示为[4]
(1)
(2)

(3)
(4)
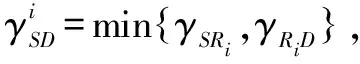
(5)
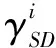
(6)
2 考虑中继时延的中继选择方法
根据文献[19]中的时延定义,第i个中继节点Ri处的中继时延可以表示为
(7)
式中,Qi表示中继节点Ri存储空间内的数据队列大小,数据按照泊松过程到达,但是数据在存储器中的队列大小与中继选择算法有关,数据队列长度Qi的统计特性难以描述,有关的研究成果未见报道,因此本文假设在一次中继选择时数据队列长度为确定的数,每次由每个中继节点反馈给源节点。当存储器没有空闲空间时,后续到达的数据将溢出,这时返回的数据队列长度为存储器空间大小。CSRi表示S-Ri链路的信道容量,CRiD表示Ri-D链路的信道容量。文献[19]所提出的中继选择方法围绕着时延因素展开,研究给定时延上限的情况下系统所能取得的信道容量。本文所提方法旨在信道容量与时延性能之间取得平衡,通过敏感因子调节信道和时延因素对中继选择结果的影响程度。当数据业务延时较大时侧重于降低数据延时,当数据业务延时较小时侧重提升信道容量。在此基础上,所提方法的思路在于,考虑利用中继时延对中继链路的等效信噪比加权,当某中继节点处的中继时延越大时,加权后的等效信噪比也应该越大,这样该中继节点被选择用于数据转发的概率才会越高,从而降低排队业务在该中继节点处的时延。基于此考虑,定义新的中继选择准则
(8)
式中Ri*表示被选择用于转发数据的第i*(i*∈Ξl)个中继节点,α为敏感因子且为正数。在实际应用中,需要选取合适的敏感因子来调整时延和信噪比对中继选择结果的影响程度。
本文所提的中继选择方法具体步骤如下:
(1)将所对应中继链路的等效信噪比大于中断门限γth的中继节点纳入候选中继集合Ξl;
(2)对候选中继集合Ξl中的任意中继节点Ri,测量计算S-Ri链路和Ri-D链路的信噪比γSRi,γRiD,并将这些信息以及各中继节点存储空间中的数据队列大小反馈给源节点;
(3)源节点根据反馈的信息,利用式(7)计算候选中继集合Ξl中各中继节点的中继时延;
(4)源节点根据式(8)选出中继节点Ri*作为转发数据的中继节点;
(5)源节点将中继选择结果通知给各中继节点。
3 性能分析3.1 中继时延的概率密度函数推导
从式(7)的定义可以看出,要想求出第i个中继节点处中继时延的PDF表达式,先要求出式中信道容量的PDF表达式,而S-Ri链路单位带宽上的信道容量(以下简称信道容量)可以表示为
CSRi=log21+γSRi
(9)

(10)
于是,CSRi的CDF可以表示为
(11)
同理,可得Ri-D链路的信道容量CRiD的CDF可以表示为
(12)

(13)
(14)

(15)
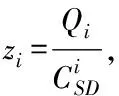
(16)
式(16)描述了第i个中继节点处的中继时延的概率密度与数据队列长度的关系。从式(16)中可以看出,第i个中继节点处中继时延的概率随着第i个中继节点的数据队列长度的增加而变大。
3.2 系统平均容量
系统平均容量可以表示为
(17)
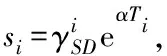
(18)
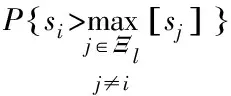
(19)
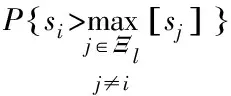
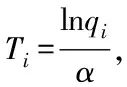
(20)
把式(16)代入式(20),qi的PDF可以化简为
(21)
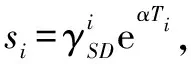
(22)
将式(6)和式(21)代入式(22),si的PDF可以化简为
(23)
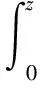

(24)

(25)
(26)
将式(24)代入式(25),接着将式(23)和式(25)代入式(26),化简后可得

(27)
根据式(17)和式(18),系统平均容量C的表达式可表示为

(28)
式(28)描述了系统的平均容量和链路平均信噪比以及敏感因α子之间的关系。系统平均容量随着链路平均信噪比的增加而增加,随着敏感因子α的增大而减小。这是由于当敏感因子增大,意味着增加了时延因素对中继选择结果的影响程度,使得数据业务在中继节点处的时延减少,然而时延的减少是以牺牲速率为代价。
3.3 中断概率
根据所提中继选择方法,只有当候选中继集合Ξl为空集即l=0的时候,系统发生中断。任意中继链路S-Ri-D发生中断的概率可以表示为
(29)
式中γth为中断门限。接着,系统的中断概率可以表示为
(30)
式(30)描述了系统中断概率与信噪比以及中继个数的关系。随着信噪比和中继个数的增加,系统的中断概率减小。
4 数值结果与分析
在这一部分,通过蒙特卡洛仿真,给出了所提中继选择方法的性能曲线,包括平均中继时延,平均容量和中断概率性能曲线,并与ORS方法的性能作对比分析。仿真中,假设无线信道服从独立同分布的瑞利衰落信道,中断门限γth=1 dB,通过仿真产生1015个信噪比随机数模拟各链路的即时信噪比。
图2描绘了平均中继时延和平均信噪比在敏感因子α=0,1,2,3,5,9时的关系。可以看到平均中继时延随着平均信噪比的增加而降低。当α=0时,意味着中继选择不考虑时延因素,所提方法等效于文献[1]中的ORS方法,此时平均中继时延最大。当敏感因子α逐渐增大,中继时延因素在中继选择方法中的影响比重也随之增大,可以发现此时平均中继时延随着敏感因子α逐渐增大而减小。需要重视的是,当敏感因子α增大到一定值时,平均中继时延继续改善的程度越来越小,说明平均中继时延并不能无限减小。
图3描绘了敏感因子α=0,1,2,3,5,9时,系统平均容量与平均信噪比的关系曲线。从图3可以看到,仿真结果和理论计算结果高度一致,验证了系统平均容量理论推导的正确性。当α=0时,所提算法等效于ORS方法,此时的系统平均容量最大。而当α≠0时,即中继选择考虑中继时延因素的情况下,系统平均容量会有所降低。值得一提的是,从图3中可以观察到,α=1时的系统平均容量与α=0时相差不大,而结合图2可以看到,α=1时的平均中继时延相对于α=0的情况却有很大的改善。因此,通过合理设置敏感因子的值,就能在保证业务速率的前提下有效降低业务时延,提高系统整体性能。

图2 平均中继时延与平均信噪比关系曲线Fig.2 Relationship between average relaying delay and average SNR
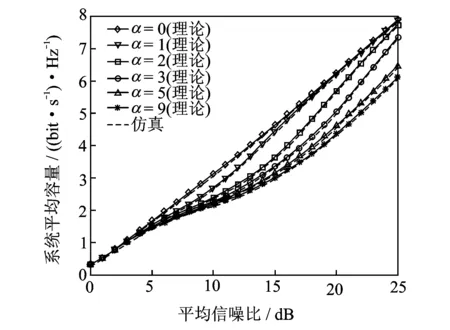
图3 系统平均容量与平均信噪比关系曲线Fig.3 Relationship between average system capacity and average SNR

图4 中断概率与平均信噪比关系曲线Fig.4 Relationship between outage probability and average SNR
图4描绘了中继节点个数N=3,4,5,6和中断门限γth=1 dB时的中断概率与平均信噪比的关系曲线。从图4可以看出,仿真结果和理论计算结果高度一致,从而验证了中断概率数学表达式的正确性。同时,可以看出,系统的中断概率随着中继个数的增加而降低,这是由于多个中继节点提供了更大的分集增益所致。
5 结束语
本文提出并验证了一种考虑中继时延的中继选择方法,获得了中继时延的概率密度函数、系统平均容量和中断概率的数学表达式。理论计算与仿真结果高度一致,验证了性能推导的正确性。数值结果同时表明:(1)平均中继时延随着敏感因子α逐渐增大而减小,但当敏感因子α增大到一定值时,平均中继时延继续改善的程度越来越小;(2)敏感因子α增大会对系统平均容量造成影响,但是通过合理设置敏感因子的值,在保证业务速率的同时能有效降低中继时延,从而提高系统的整体性能;(3)与文献中的方法一样,对于所提方法,增加中继节点数目能提供更大的分集增益,从而改善系统的中断性能。
