物理实验中测量不确定度的评定与表示

刘鹏

(宿州学院机械与电子工程学院，安徽宿州 234000)

1 引言

在物理实验测量中，测量的目的是为了得到测量结果，测量结果的质量如何，用不确定度来说明.在不确定度产生以前，物理实验结果的质量好坏都是用误差大小来表示的，但是由于误差的定义及计算方法不完善，世界各国对误差的具体应用和计算规则并不相同，从而影响了国际间的交流和科研成果的推广.因此，国际计量局(BIPM)于1980年提出了实验不确定度建议书INC-1.此建议书的提出，动摇了传统的误差理论体系.经过多年努力，1992年国际计量大会终于制定了协调的、具有国际指导性的《测量不确定表达指南》［1-2］.1993年，此《指南》由各国际组织批准实施，供各国使用，为实验不确定度的统一奠定了基础.

2 不确定度的概念

不确定度是与测量结果相关联的一个参数，用以表征测量值可信赖的程度，它表示由于测量误差的存在而对被测量不能确定的程度，不确定度的大小反映出测量结果的优劣，不确定度越小，则表示测量结果越接近真实值，其使用价值越高.在物理实验中，没有不确定度说明的实验结果是不完整的，甚至可以说是没有意义的［2-3］.

不确定度一般由多个组成分量，按其数值的评定方法可归并成两类:(1)A类分量，由观测列统计分析评定，也称统计不确定度(多次等精度测量)，记作△A;(2)B类分量，不用统计分析评定，也称非统计不确定度(单次测量、仪器误差、估计误差)，记作△B.A类分量和B类分量的合成应按方差合成原理进行，其中σAB为两类分量中任意两个不确定度间的协方差［3］.

3 标准不确定度的评定与表示

3.1 A类不确定度的评定

由于偶然效应，被测量X的多次重复测量值x1，x2，…，xn将是随机的，从随机的测量值出发，用统计的方法评定标准不确定度，就是标准不确定度的A类评定，设A类标准不确定度为μA(x)，由贝塞尔公式得到实验标准差

平均值的标准偏差

A类评定标准不确定度(又称标准不确定度的A类分量)就取为平均值的标准偏差，即μA(¯x)=S (¯x).按误差理论的高斯分布，如果不存在其它误差影响，则量值范围［¯x-μA(¯x)，¯x+μA(¯x)］中包括其值的概率为68.3%［4］.

3.2 B类不确定度的评定

在多数情况下，只能取仪器误差作为单次测量结果的误差，或者根据测量条件、仪器误差以及测量者的技术对单次测量结果的误差作出恰当的符合实际的估计，这一类的评定就是B类评定［5］.

在进行B类评定时，首先要知道测量仪器的“最大允许误差”△仪.此类误差一般可视为均匀分布，而△仪为均匀分布的标准差，则B类评定不确定度(又称标准不确定度的B类分量)μB(x)为:

严格讲，从△仪求μB(x)的变换系数与实验分布有关，在此均近似按均匀分布处理［5-6］.

例如，用△仪=0.02mm的游标卡尺测量某物的长度，测量数据为29.18，29.25，29.29，29.26，29.23，29.25.则由游标卡尺引入的B类分量μB(x)为:

4 合成标准不确定度与展伸不确定度

4.1 合成标准不确定度

若待测量y=f(x1，x2，…，xn)，其中x1，x2，…为相互独立的直接测量量，则合成标准不确定度μ(y)用下式可求:

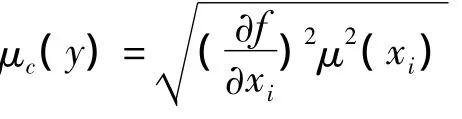
式中σk或σi可为si，μi中的任何一个，σkl为相关系数(-1≤σkl≤1).当各分量完全正或负相关时，σkl分别为1，-1，得线性合成法;当各分量无关，各自独立时，σkl=0，得方根合成法.其值在测得值±uc区间的置信概率约为0.68，其有效自由度为:

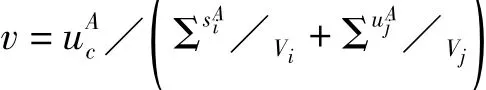
实验中偏微商∂f/∂xi是在估计值xi处取值.

对A类和B类评定的合成可按方差合成方法

式中vi为si的自由度，如sj用贝塞尔法估计时，vi=n-1，n为等精度测量的次数;vj为uj的自由度，式中为估计的uj的相对误差，当无法估计时，可取vj= 1［6-7］.

4.2 扩展不确定度

扩展不确定度又称总不确定度，用U来表示.扩展不确定度是由合成标准不确定度uc乘以k而得，即U=k·uc，其中k是与置信概率相联系的包含因子.近似正态分布，k常用t分布的置信因子tp(v)求得，即k=tp［7］.在这里，v为合成标准不确定度的有效自由度.

5 不确定度应用举例

例如:测量合金圆柱体的密度，求其标准不确定度.m=14.00g，最大允差0.04g.

表1 圆柱体底面直径与高的测量值

解:表1中的数据为测量值，由表中的数据可知:

圆柱体直径的平均值为:

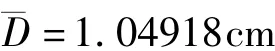
直径的不确定度:

圆柱体高的平均值为:

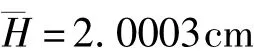
高的不确定度:

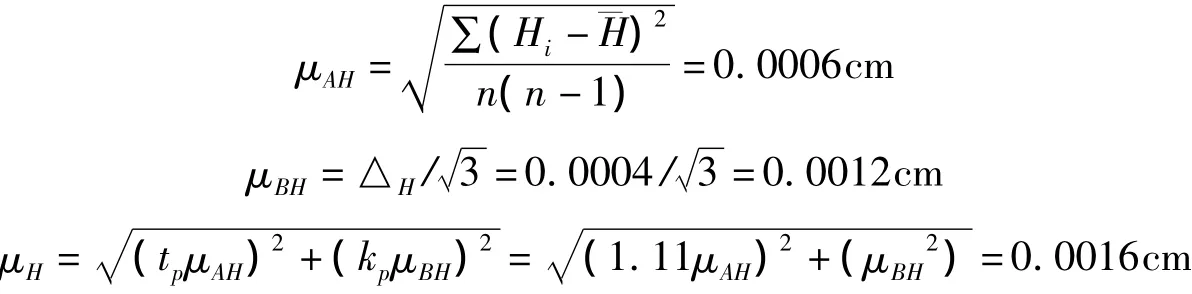
质量不确定度:

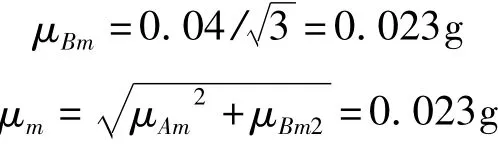
密度:

由传递公式:

密度的标准不确定度:

6 结语

由上述讨论可知，在物理实验中引入不确定度理论新体系，是物理实验教学改革的一个重要环节.它弥补了原误差理论在定义，分类方法及计算方法上的某些不足，因此更科学合理.用不确定度来表示实验结果，能够更好的培养学生的实验结果评价能力，从而大大的提高学生的实验素质.

［1］国际标准化组织.测量不确定度表达指南［M］.肖明辉，康金玉，译.北京:中国计量出版社，1994.

［2］倪育才.实用测量不确定度评定［M］.北京:中国计量出版，2004.

［3］刘智敏.不确定原理［M］.北京:清华大学出版社，1993.

［4］杨述武.普通物理实验(第3版)［M］.北京:高等教育出版社，2003.

［5］丁慎训，张孔时.物理实验教程［M］.北京:清华大学出版社，1992.

［6］胡其图.物理实验教程［M］.北京:气象出版社，1999.

［7］刘智敏.不确定度与分布合成［J］.物理实验，1999，19(5):58.