一种低阶大气环流模型的全局指数吸引集估计

孔宪明，鞠培军

(泰山学院数学与统计学院，山东泰安 271021)

1 引言

最近十多年来，混沌控制和同步得到广泛而深入的研究［1－2］，其中许多结论的证明都用到了混沌系统最终有界的假设，因此，混沌系统的最终有界性证明非常重要.由于混沌系统的方程组是非线性的，进行纯理论分析较困难.直到2002年，Tucker用计算机辅助方法严格论证了Lorenz吸引子存在性的信息［3］.俄罗斯学者Leonov针对Lorenz系统，得到系统全局吸引集的一个圆柱形估计式和一个球形估计式，这是典型混沌系统第一个全局最终有界的结果［4］.廖晓昕等通过构造广义正定、径向无界Lyapunov函数，给出了Lorenz系统全局指数吸引集的统一结果，囊括了目前一些类似结果为特例［5－7］.最近，我们针对广义Lorenz系统，通过线性变换和构造Lyapunov函数，给出了系统全局指数吸引集估计的新方法，得到了最终有界的精确估计式.

文献［8］提出了一个新的低阶大气环流模型

当a=1/4，b=10，G=2.1，F=7时，上述系统有一个混沌吸引子，如图1所示.

文献［8］讨论了该系统吸引子的特征，并数值模拟了系统从分歧到混沌的过程.对于这种混沌模型吸引子的研究还没看到.本文将研究这类大气环流模型的吸引子存在性问题，给出一个全局指数吸引集的估计式，所得系统的有界性结果将为进一步研究奠定了很好的基础.

2 问题描述

类似文献［5－7］，我们称

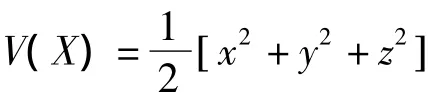
图1 系统(1)的混沌吸引子

当t→+∞时，称Ω={X|V(X)≤L}为式(1)的一个全局吸引集.若∀X0∈Ω，∀t＞t0，X(t，t0，X0)⊂Ω，则称Ω为正向不变集.

若还存在r＞0，∀X0∈3，当V(X0)＞L，且V(X(t))＞L时，存在指数估计式V(X(t))－L≤(V(X0)－L)e－r(t－t0)则称Ω为式(1)的一个全局指数吸引集.

3 全局指数吸引集

为式(1)的广义正定、径向无界的Lyapunov函数，其中X=(x，y，z).

定义1［5－7］若存在正数L＞0，则对于V(X0)＞L，且V(X(t))＞L，有

1=0，因此f1(x，y)在(x1，y1)达到全局极大值.

有

利用比较定理对式(2)两边进行积分有

从而当V(X(t))≥L1，V(X0)≥L1时，有全局指数估计式

有

故有

分别对式(3)、(5)两边取上极限，便有

即

推论1 当F=G=0时，系统(1)的平衡点(0，0，0)全局指数稳定.

推论2 对于控制系统

设计常数控制器:u1=－aF，u2=－G，则控制系统的平衡点(0，0，0)全局指数稳定的.

当a=1/4，b=10，G=2.1，F=7时，设计以上常数控制器，仿真如图2所示.

图2 控制系统(6)的常数控制仿真图

4 结论

本文利用广义Lyapunov函数方法估计了一种低阶大气环流模型最终有界的问题，给出了全局指数吸引集的估计式.混沌系统的最终有界性将为进一步研究控制和同步奠定基础，本文所得结果具有一定的理论和实际意义.

［1］陈关荣，吕金虎.Lorenz系统族的动力学分析、控制与同步［M］.北京:科学出版社，2003.

［2］杨万利，王铁宁.非线性动力学理论及应用［M］.北京:国防工业出版社，2007.

［3］TuckeW.A rigorous ODE solver and Smale’s14 problem［J］.Found Comput Math，2002(2):53－117.

［4］Leonov G A.Bound for attractors and the existence of Hornoclinic orbits in the Lorenz system［J］.JApplMathmech，2001，65(1):19－32.

［5］廖晓昕.论Lorenz混沌系统全局吸引集和正向不变集的新结果及对混沌控制与同步的应用［J］.中国科学E辑:信息科学，2004，34(12):1404－1419.

［6］廖晓昕，罗海庚，傅予力，等.论Lorenz系统族的全局指数吸引集和正向不变集［J］.中国科学E辑:信息科学，2007，37(6):757－769.

［7］Liao X X，Fu Y，Xie S，Yu P.Globally exponentially attractive sets of family if Lorenz systems［J］.Science in China(Ser F)，Information Sciences，2008(51):283－292.

［8］Shilnikov A，Nicolis G，Nicolis C.Bifurcation and predictability analysis of a low order atmospheric circulation model［J］.International Journal of Bifurcation and Chaos，1995(5):1701–1711.