基于微裂纹统计模型的PBX 力学行为

郭 虎，罗景润

（中国工程物理研究院总体工程研究所，四川 绵阳621900）

引 言

高聚物黏结炸药（polymer bonded explosive，PBX）PBX 是一种颗粒高度填充的复合材料。从细观研究可以看出［1-4］，PBX 含有初始损伤，在外加载荷的作用下，这些损伤会进一步演化，以颗粒断裂、界面脱粘、黏结剂基体开裂、变形孪晶以及剪切带等形式使炸药的力学性能劣化。同时，PBX的起爆机理（特别是XDT）与损伤也有密切的联系。因此，对PBX 细观损伤的表征是其力学行为研究的重要内容，也是武器安全性研究的基础。

目前，已有不少本构模型应用于PBX力学行为的研究，如修正的Ramberg-Osgood模型［5］、Johnson-cook模型［6］和罗景润等［7］结合前两者而建立的模型，以及周风华等［8-9］建立的损伤型ZWT 模型。但是，这些本构模型都没有较好地表征PBX 细观损伤。微裂纹统计模型（Statistical Crack Mechanics，SCRAM）是基于微裂纹扩展的本构模型［10-11］，利用微裂纹尺寸表征材料细观损伤，能较好地反映材料细观物理过程［12-13］。本研究基于微裂纹统计模型，分析了PBX 的力学行为及相应的物理过程，以及黏性对PBX 力学行为的影响。

1 模型的建立

由于考虑的因素较多，SCRAM 本构模型本身比较复杂，为方便应用，相继出现了各向同性ISOSCRAM 模型［14］和在其基础上建立的黏弹性Visco-SCRAM 模型［15-16］。如图1所示，Visco-SCRAM模型由一个包含多个Maxwell体并联的黏弹性体和一个由SCRAM 模型定义的微裂纹损伤体串联而成。其中，是偏应力率，是黏弹性偏应变率，是微裂纹损伤体的偏应变率，而Gn和ηn分别是第n个Maxwell体的剪切模量和黏性系数。

在第n个Maxwell体里，有：

图1 Visco-SCRAM 模型结构图［15］Fig.1 Schematic representation of Visco-SCRAM model［15］

由于弹簧与黏壶串联，故黏弹性应变率等于弹簧与黏壶产生的应变率之和，即：

故第n个Maxwell体的偏应力率为：

即

式中：τ（n）=η（n）／G（n）是 第n个Maxwell体 的 松 弛时间。

对于由多个Maxwell体并联的黏弹性体，其偏应力S是各Maxwell体的偏应力的和，即：

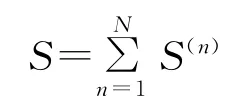
所以黏弹性体的偏应力、偏应力率和偏应变率的关系可以表示为：

对于整个模型，总的偏应变率为黏弹性偏应变率和微裂纹损伤体的偏应变率的和，即：

微裂纹损伤体的偏应变和偏应力的关系可表示为［15］：

其中，βe是与剪切模量G和初始裂纹分布N0相关的参数，c是微裂纹平均半径，

式中：A 是常数；a为初始缺陷尺寸。

将其代入（3）式，可以得到：

写成率的形式为：

联立方程（1）、（2）和（4），得到：

另外，模型假设体应变εm和体应力σm的关系为：

式中：k为材料的体积模量。

模型中含有微裂纹扩展速率，该变量难以测量。根据实验观察与总结［16］，微裂纹扩展速率主要依赖于应力强度因子。本研究利用Dienes和Johnson等［17-18］总结的经验公式对应力强度因子和微裂纹扩展速率进行计算。

2 数值计算与分析

将本构方程在单轴应力下进行简化，即将式（5）和（6）进行简化，得到（v为泊松比）：

利用中心差分的方法，将上述微分方程组转化为增量形式，可得：

和

由上述单轴应力情况下增量形式的本构方程和文献［16］给出的关于PBX9501 的参数，可拟合得到不同加载方式和不同应变率下的应力应变关系曲线。PBX9501中的颗粒（HMX）和黏结剂质量分数分别为95%和5%。

2.1 拉伸和压缩曲线分析

由于在拉伸和压缩下的损伤机理不同，PBX 存在着明显的拉伸和压缩不对称性［7］。PBX 的拉伸强度要比压缩强度小很多，通常在一个量级左右。图2是通过Visco-SCRAM 模型拟合出的拉伸和压缩下的应力应变曲线（应变率1／s），可以看出，两者明显不对称，且其拉伸和压缩的强度和模量与实验结果基本一致。所以，Visco-SCRAM 模型能够反映PBX 的拉压不对称性，而模型的这一特征来自应力强度因子的计算公式。

图2 Visco-SCRAM 单轴拉伸与压缩曲线Fig.2 Simulated stress-strain response under uniaxial tension and compression

PBX 是一种应变率相关材料，在拉伸与压缩状态下，PBX 的模量和强度均随应变率的增大而增加。图3和图4分别是通过Visco-SCRAM 模型拟合出的拉伸与压缩状态的单轴应力-应变曲线。可以看出，两种状态下的曲线均有明显的应变率效应，模量和强度均随应变率的增大而增加，且在高应变率（101～103s-1）下更加明显。

另外，在相对较低的应变率（＜10s-1）下曲线的硬化效应并不明显，在软化之前应力应变几乎呈线性关系，而在应变率较高时则表现出明显的硬化效应。这种硬化不明显的现象与模型选取的黏性参数有关。

计算采用PBX9501相关参数，其压缩状态下的计算值与实验结果吻合较好，两者的强度与模量在进入软化阶段前均相近（如图5）。其中，准静态实验结果来自Wiegand等［19］的工作，动态数据来自Dobratz等［20］的工作。进入软化阶段后，动态与准静态的计算值与实验结果均相差较大，说明Visco-SCRAM 模型不能较好地模拟PBX 的软化阶段，这可能是出现宏观裂纹造成的。由于准静态情况下计算曲线中的硬化效应不明显，其拟合结果与实验结果的差异比动态情况大。所以，Visco-SCRAM模型更适合于模拟PBX 在动态情况下的力学行为。

由以上结果可以看出，Visco-SCRAM 模型能较好地反映PBX 的模量和强度随应变率增大而增加的特征，且其模量和强度的计算值与实验结果吻合较好。但该模型只能模拟PBX 软化前的阶段，软化阶段的误差较大。

图5 准静态和动态压缩情况下应力-应变的拟合结果与实验Fig.5 Comparison of the stress-strain responses calculated by Visco-SCRAM with data under static and dynamic compression

2.2 物理过程分析

SCRAM 模型的建立是基于细观微裂纹的扩展，微裂纹的平均半径和微裂纹的扩展速率是其中的重要变量，它们会随着加载的过程而变化。

单轴压缩应力-应变曲线和其过程中微裂纹平均半径随应变的变化情况见图6和图7。

其中c／c0表示微裂纹平均半径与初始平均半径的比值。从微裂纹平均半径与应变的关系可以看出，初始的A点到B的过程中，微裂纹平均半径基本不变，即c／c0≈1。当到达B点后，应力足够大，致使微裂纹开始快速扩展，微裂纹半径也快速增大。在C点，达到应力峰值，此时微裂纹平均半径大约是初始半径的10倍，即c／c0≈10。通过对各应变率下压缩加载的分析，到达应力峰值时的微裂纹平均半径随应变率的增大而增大（如应变率为103s-1时，c／c0≈16）。另外，在拉伸情况下（10s-1），到达应力峰值时的微裂纹平均半径只是初始半径的两倍（c／c0≈2），明显小于同等应变率下压缩的情况。在其他应变率下分析也能得到同样的规律，即对于应力峰值时的微裂纹平均半径，拉伸加载下明显小于压缩的情况。经过应力峰值之后，由于微裂纹半径过大，微裂纹聚合、生长，使材料发生宏观的破坏，致使材料进入软化阶段（C—D）。上述分析能在一定程度上反映材料的细观物理过程。

微裂纹是PBX 主要的损伤类型，而SCRAM 模型能从微裂纹扩展的角度描述PBX 在受载过程中的细观物理过程，这将有助于研究PBX 宏观力学行为与细观物理过程的联系。

2.3 黏性对PBX 力学性能的影响

PBX 的黏性主要来自黏结剂，黏结剂越少，黏性对PBX 力学行为的影响越小。Visco-SCRAM 模型里的黏性主要来自广义Maxwell体里的松弛时间，表1中关于黏性的参数是通过半经验的方式得到的。首先通过实验得到PBX 的模量与应变率的关系，然后半经验地假设松弛时间是应变率倒数的十分之一，从而通过最小二乘法拟合数据点得到松弛时间与模量的关系，即应力松弛谱。Bennett等［15］通过该方法得到PBX9501的松弛时间与模量呈对数关系（见图8）：

式中：m1=-0.17 077；m2=0.06 825；m3=7.1 679；E和τ的单位分别为MPa和s。

图8 PBX9501杨氏模量与松驰时间的关系［15］Fig.8 The young′s modulus versus relaxation time data for PBX9501［15］

本研究假设松弛时间是应变率倒数的10-（q+1）倍，则可在表1给出的黏性参数的基础上得到新的黏性参数组。显然，当q＜0 时，黏性减小；当q＞0时，黏性增大。图9 是不同黏性参数下Visco-SCRAM 模型单轴压缩应力应变曲线（10s-1）。从图9可以看出，黏性增大和减小对压缩曲线的影响是不对称的。当黏性增大时，模量略有减小，强度几乎没有变化，而q＞2后，模量和强度都不会有明显的变化。当黏性减小时，模量有明显的增大，强度在q＜-1后也有明显的增大，而q＜-4后，模量和强度都不会有明显的变化。

图9 黏性对Visco-SCRAM 压缩应力—应变曲线的影响Fig.9 Effect of viscosity on the predicted stress—strain response under compression

以上分析说明，黏性的变化对PBX 力学性能的影响较明显。黏性增大时，模量和强度会随之减小；黏性减小时，模量和强度会增大。其中，存在一定的范围（-1＜q＜2）内，可以使PBX 的模量变化，而强度几乎保持不变。对于以上黏性增大减小时的不对称，可能是因为PBX9501 的黏性本身就比较大。

3 结 论

（1）SCRAM 模型能较好地反映PBX 在拉伸和压缩下的力学行为和相应的细观物理过程，对于疲劳、蠕变以及断裂等行为，还需更加深入的研究。

（2）在压缩或拉伸过程中，应力较小时，微裂纹平均半径基本保持不变。随着应力的增大，微裂纹扩展速率增大，当微裂纹扩展到一定长度时会使PBX 产生破坏。到达应力峰值时，微裂纹平均半径随应变率的增加而增大，且该值在拉伸时明显比压缩时小。

（3）减小PBX 的黏性，模量明显增大，破坏应变明显减小。对于破坏应力，存在一个阈值，当黏性减小量小于这个阈值时，破坏应力基本不变，超过这个阈值后，破坏应力明显增大。

［1］陈鹏万，黄风雷.含能材料损伤理论及应用［M］.北京：北京理工大学出版社，2006.

CHEN Peng-wan，HUANG Feng-lei.Damage theory and application of energetic material［M］.Bejing：Beijing Institute of Technology Press，2006.

［2］Palmer S J P，Field J E，Huntley J M.Deformation，strengths and strains to failure of polymer bonded explosives［J］.Proc R Soc Lond A，1993，440：399-419.

［3］Rae P J，Goldrein H T，Palmer S J P，et al.Quasistatic studies of the deformation and failure ofβ-HMX based polymer bonded explosives［J］.Proc R Soc Lond A，2002，458：743-762.

［4］Trumel H，Lambert P，Belmas R.Mesoscopic investigations of the deformation and initiation mechanisms of a HMX-based pressed composition［C］／／14th International Detonation Symposium.Coeurd Alene：［s.n.］，2010.

［5］董海山，周芬芬.高能炸药及其相关物性［M］.北京：科学出版社，1989.

［6］Johnson G R，Cook W H.A constitutive model and data for metals subjected to large strain，high strain rates，and high temperature［C］／／7th International Symposium on Ballistics.Hague：［s.n.］，1983：1-7.

［7］罗景润.PBX 的损伤、断裂及本构关系研究［D］.绵阳：中国工程物理研究院，2001.

LUO Jing-run.Study on damage，fracture and constitutive relation of PBX［D］.Mianyang：CAEP，2001.

［8］周风华，王礼立，胡时胜.有机玻璃在高应变率下的损伤型非线性黏弹性本构关系及破坏准则［J］.爆炸与冲击，1992，12（4）：333-342.

ZHOU Feng-hua，WANG Li-li，HU Shi-sheng.A damage-modified nonlinear visco-elastic constitutive relation and failure criterion of pmma at high strain-rates［J］.Explosion and Shock Waves，1992，12（4）：333-342.

［9］李英雷，李大红，胡时胜，等.TATB钝感炸药本构关系的实验研究［J］.爆炸与冲击，1999，19（4）：353-359.

LI Ying-lei，LI Da-hong，HU Shi-sheng，et al.An experimental study on constitutive relation of TATB explosive［J］.Explosion and Shock Waves，1999，19（4）：353-359.

［10］Dienes J K.Foundations of statistical crack mechanics［C］／／International Symposium on Intense Dynamic Loading and Its Effects.Beijing：Pergamon Press，1986：602-607.

［11］Dienes J K.Statistical Crack Mechanics R LA-UR-93-4254［R］.Los Alamos：LANL，1993.

［12］Zuo Q H，Addessio F L，Dienes J K，et al.A rate-de-pendent damage model for brittle materials based on the dominant crack［J］.International Journal of Solids and Structures，2006（43）：3350-3380.

［13］Zuo Q H，Toutanji H A.Modeling damage in concrete pavements and bridges，UTCA Report 09301［R］.Alabama：UTCA，2010.

［14］Addessio F L，Johnson J N.A constitutive model for the dynamic response of brittle materials［J］.Journal of Applied Physics，1990，67（7）：3275-3286.

［15］Bennett J G，Haberman K S，Johnson J N，et al.A constitutive model for the non-shock ignition and mechanical response of high explosives［J］.Journal of the Mechanics and Physics of Solids，1998，46（12）：2303-2322.

［16］Robert M H，Bennett G.An implicit finite element material model for energetic particulate composite materials［J］.International Journal for Numerical Meth-ods in Engineering，2000，49（9）：1191-1209.

［17］Dienes J K.Strain-softening via SCRAM LA-UR-98-3620［R］.Los Alamos：Los Alamos National Laboratory，1998.

［18］Dienes J K，Kershner J D.Multiple-shock initiation via statistical crack mechanics［C］／／11th International Detonation Symposium. Snowmass： Snowmass CO，1998.

［19］Wiegand D A.Mechanical failure properties of composite plastic bonded explosives［C］／／Schmidt D P，Dandekar D P，Forbes J W.Shock Compression of Condensed Matter-1997.Woodbury： AIP， 1997：599-602.

［20］Dobratz B M.Properties of chemical explosives and explosive stimulants，UCRL-51319［R］.Livermore：Livermore National Laboratory Report，1974.