含铝炸药JWL状态方程参数的确定

计冬奎，肖 川，杨 凯，韩天一，袁秋长

（西安近代化学研究所，陕西 西安710065）

引 言

压装含铝炸药已广泛应用于各类常规兵器，尤其在侵彻战斗部中得到了大量的应用［1-2］。炸药爆轰产物状态方程是描述炸药爆轰C-J状态之后的爆轰产物系统各物理量（压力、比容、温度和内能等）之间的关系式。对压装含铝炸药爆轰产物状态方程的研究，可以为装填含铝炸药侵彻类战斗部设计提供基础数据。

目前，已有多种比较成熟的爆轰产物状态方程。其中，JWL（Jones-Wilkins-Lee）状态方程是一种能比较精确地描述爆轰产物的膨胀驱动过程［3］，且可由试验方法确定的半经验状态方程。JWL 状态方程还可以精确地描述爆炸加速金属过程中爆轰产物的压力-体积-能量特性［4］。陈朗等利用圆筒试验研究了含铝炸药（RDX76%／Al20%wax4%）的JWL状态方程［5］。本研究对两种不同尺寸压装含铝炸药进行了圆筒试验，得到其JWL 状态方程参数，为其更深入研究提供参考。

1 实验部分

1.1 圆筒试验与结果

实验用压装含铝炸药为以RDX 为主要成分，采用压装成型工艺，样品尺寸分别为Φ25mm×300mm（壁厚2.5mm）和Φ50mm×495mm（壁厚5.0mm）；圆筒材料为TU1 无氧铜；狭缝位置分别为距圆筒起爆端200mm 和295mm。试验装置如图1所示。

圆筒试验确定了炸药爆轰产物侧向膨胀作功的标准试验方法［6］，该方法可以定量比较各种炸药的作功能力，并可将试验数据处理成JWL 状态方程，用于理论计算。试验采用高纯度（99.99%铜含量）的铜管，内装炸药，使其产生一维平面爆轰波，利用同步氩气弹发光，对准圆筒某一截面，利用条纹扫描相机记录该截面表面位移与时间的关系，经过数据处理可获得该截面的时间—速度—位移曲线，求出铜管在爆轰产物驱动下的速度历程。

对Φ25mm 和Φ50mm 压装含铝炸药各进行3发试验。狭缝位置处的圆筒在爆轰产物驱动下的膨胀过程光测结果如图2所示。

图1 圆筒试验装置示意图Fig.1 Schematic diagram of the cylinder tests

图2 压装含铝炸药圆筒膨胀过程照片Fig.2 A photograph of the cylinder expansion process for aluminized explosive

按照拍摄到的圆筒膨胀试验扫描图像底片，可以得到筒壁飞散运动轨迹，圆筒膨胀示意图如图3所示。

图3 圆筒膨胀示意图Fig.3 Schematic diagram of the cylinder expansion

1.2 圆筒膨胀速度的计算

按照GJB772.308-93［7］，从一端起爆装填在圆筒内的炸药，炸药爆轰后圆筒壁在爆轰产物作用下沿圆筒的径向和轴向作二维运动，膨胀距离（RR0）与膨胀时间t满足下式：

圆筒的径向膨胀速度u为：

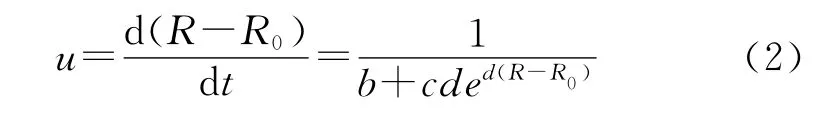
式中：t为拟合后的膨胀时间；a、b、c、d均为拟合系数。按最小二乘法原理对光测结果进行曲线拟合，可获得系数a、b、c、d的值。

2 JWL状态方程参数的确定

2.1 基本方法概述

首先用解析分析方法求解出JWL 状态方程参数［8］，然后以这些参数为预估参数，用LS-DYNA 数值模拟计算压装含铝炸药两种尺寸圆筒的膨胀过程［9］，通过迭代优选方法，求出该炸药爆轰产物JWL状态方程的参数值。

2.2 解析求解方法

JWL方程的形式为：

等熵条件下，其形式为：

式中：p为爆轰产物的压力，V为爆轰产物的相对比容。该状态方程有6个待定参数，其等熵形式（4）式的6个待定参数为A、B、C、R1、R2和ω。

式（4）经转换可得以等熵内能形式表示的JWL状态方程，其形式为［8］：

式中：Es为爆轰产物的等熵内能。

等熵内能可以通过下式获得：

对于圆筒试验：

式中：E为爆轰产物气体膨胀释放的有效总能，即爆热Q；Eg为Gurney能；u为壁速；mM为单位长度铜管质量，mE为单位长度炸药质量；u为被驱动金属的速度。

为将能量守恒关系式与圆筒实验测试得到的圆筒膨胀过程联系起来，须知相对比容V随膨胀距离（R-R0）的变化关系。通过二维流体动力学数值模拟计算，拟合得到一般炸药的Φ25mm 圆筒试验的关系为：

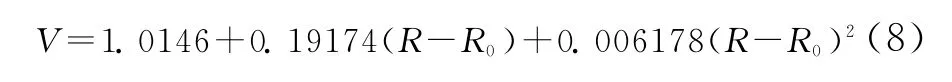
由上述关系式和圆筒试验测试结果的联立方程组，就可解析求解出JWL状态方程的6个参数估算值。JWL 状态方程（5）式的右边3项，可分别视为高压、中压和低压3个阶段的贡献项：

在低压阶段（V＞6），可取

通过对V＞6 阶段的试验参数进行计算，可求解得到C和ω。

在中压阶段（2＜V＜5），可取：

由（9）求解得到的C和ω，通过对该中压阶段的试验参数进行计算，得到B和R2。

A和R1可由C-J参数确定。在C-J点，有：

由实测爆压pC-J、爆速D、多方指数λ，和已经求解B、R2、C和ω，可求得A和R1。

3 结果与讨论

3.1 数值计算结果

在LS-DYNA 程序计算圆筒爆炸的二维轴对称问题中，建立了Lagrange坐标（R，Z，t），即质量的原始坐标为（R，Z），计算中跟踪质量，按照实验中标用的尺寸。

计算中，不计爆轰波的结构仍采用瞬时爆轰模型，即LS-DYNA 中的“MAT-HIGH EXPLOSIVEBURN”模型，不计炸药的强度效应，只要给出密度、爆速与爆压即可。另外，在Lagrange计算中，适用“EOS-JWL”模型，除了需要给出JWL 方程中的A、B、C、R1、R2和ω预估值外，还必需给出初始能量（即爆热E0）和初始相对体积。

经多次修正和计算，压装含铝炸药Φ25mm 圆筒试验模型的膨胀过程R（t）计算结果与试验结果基本相符。再将压装含铝炸药Φ25mm 圆筒试验计算得到的参数作为预估参数代入压装含铝炸药Φ50mm 圆筒试验模型进行数值模拟计算，并对参数作微量调整，直至计算结果与试验测试结果基本一致。压装含铝炸药两种装药直径圆筒试验圆筒膨胀过程数值模拟计算结果与测试结果进行比较，结果见图4。可以看出，测试结果与数值模拟结算结果的相对误差基本控制在1%左右，符合JWL 状态方程参数确定的要求。

图4 含铝炸药圆筒试验中圆筒膨胀过程的计算值与测试结果Fig.4 Calculated values and experimental ones of expansion process for cylinder test of aluminized explosive

3.2 JWL状态方程参数

通过对压装含铝炸药两种装药直径圆筒试验的数值计算和综合分析，得到压装含铝炸药爆轰产物的JWL 状态方程参数，见表1。炸药密度为1.868g／cm3。

表1 含铝炸药JWL状态方程参数Table 1 Parameters of JWL equation of state for detonation products of aluminized explosive

4 结 论

（1）得出压装含铝炸药JWL 状态方程参数A、B、C、R1、R2、W分 别 为 2.92GPa、12GPa、0.583GPa、4.95、1.02、0.53.

（2）Φ50mm 圆筒膨胀至60mm 处的速度高于Φ25mm圆筒膨胀至30mm处的速度，Φ50mm 圆筒与Φ25mm 圆筒的JWL 状态方程参数有一定的差异，这表明压装含铝炸药的作功能力与JWL状态方程参数存在尺寸效应。

［1］孙业斌，惠君明，曹欣茂.军用混合炸药［M］.北京：兵器工业出版社，1995：364-483.

［2］董军，赵省向，韩仲熙，等.黏结剂对含铝炸药造型粉流散性和堆积密度的影响［J］.火炸药学报，2009，32（4）：53-55.

DONG Jun，ZHAO Sheng-xiang，HAN Zhong-xi，et al.Effect of binder on the flowability and packing density of aluminized explosive moulding power［J］.Chinese Journal of Explosives and P ropellants，2009，32（4）：53-55.

［3］Lee E L.Adiabatic expansion of high explosive detonation products，UCRL-50422［R］.San Francisco：University of California，1968.

［4］张宝坪，张庆明，黄风雷.爆轰物理学［M］.北京：兵器工业出版社，2006：153.

［5］陈朗，冯长根，黄毅民.含铝炸药圆筒试验及爆轰产物JWL状态方程研究［J］.火炸药学报，2001，24（3）：13-15.

CHEN lang，FENG chang-gen，HUANG yi-min.The study on JWL equation of state and cylinder test for aluminized explosive［J］.Chinese Journal of Explosives and Propellants，2001，24（3），13-15.

［6］Kury J W.Metal acceleration by chemical explosive.［C］／／4th Symp on Detonation.Portland：Office of Naval Research，1965：3-13.

［7］GJB 772A-97.炸药试验方法［S］.北京：国防科工委军标出版发行部，1997：290-299.

［8］Miller P J.Determing JWL Equation of State Parameters Using The Gurney Equation Appraximalion／／［C］9th Symp on Detonation Portland Office of Naval Research，1989：498-505.

［9］时党勇.基于ANSYS／LS-DYNA 8.1 进行显示动力分析［M］.北京：清华大学出版社，2005：184-195.