中原经济区城市经济发展水平的竞争力评价

郭国峰，张 玮(郑州大学 商学院，河南 郑州 450001)

中原经济区规划起草于2010年，是在现任河南省委书记卢展工主持下规划设立的综合性经济区。它在2011年被列入《全国主体功能区规划》，正式成为国家战略。2011年3月17日公布的《国民经济和社会发展第十二个五年规划纲要》明确提出重点推进中原经济区等区域发展。中原经济区的范围包括河南全省、安徽西北部、山东西南部、河北南部和山西东南部。具体包括河南省的18个省辖市，安徽的淮北、宿州、阜阳、亳州，山东的菏泽、聊城，河北的邯郸、邢台以及山西的晋城、长治、运城，共29个省辖市，土地面积28万平方公里,区域内近1.58亿人口，占全国人口总量的11.83%。全区1.9亿亩耕地，占全国的1/10以上。

中原经济区作为国家层面重点开发区域，位于全国“两横三纵”城市化战略格局中陆桥通道和京哈、京广通道纵轴的交会处，包括以郑州为中心的中原城市群部分地区。它是沿海地区发展的重要支撑，是中部崛起的重要基地，是继“长三角”、“珠三角”、“京津冀”三大经济区之后，于2010年由豫鄂皖晋鲁冀6省29市组成的经济区域。该区域的定位为全国重要的高新技术产业、先进制造业和现代服务业基地，能源原材料基地、综合交通枢纽和物流中心，区域性的科技创新中心，中部地区人口和经济密集区。

一、指标体系的建立

1.指标选取原则

数据的选取主要遵循三个基本原则：一是数据的可得性原则;二是数据的全面性,即尽量避免出现某个城市数据的缺失;三是数据的现实意义,即考虑中国国情与区域发展的实情。

2.指标选择

竞争力评价需要建立一个能描述区域竞争力的模型，选择一个反映该区域经济发展水平的指标体系。为客观评价中原经济区各城市经济发展水平，在选择指标时必须遵守全面性原则、科学性原则和整体性原则。具体的评价指标主要有以下几项。

(1)X1：地方生产总值(GDP)，衡量经济发展的总体规模。

(2)X2：人均GDP，反映人民生活水平及富裕程度。

(3)X3:GDP增长率，反映城市的发展速度。

(4)X4:社会消费品零售总额，反映一定时期内人民物质文化生活水平的提高情况，社会商品购买力的实现程度以及零售市场的规模。

(5)X5：全社会固定资产投资总额，反映固定资产投资规模、速度、比例关系和使用方向。

(6)X6：地方财政收入，反映政府的经济实力。

(7)X7：城镇居民人均可支配收入。它是反映区域城镇发展程度的指标之一。

(8)X8：农村居民人均纯收入。它是反映区域农村发展程度的指标之一。

(9)X9：进出口总额。它是反映区域经济开放程度及财富的指标之一。

(10)X10：规模以上工业企业增加值。反映规模以上工业企业在经济中的作用。

二、因子分析

1.因子分析的基本原理

因子分析的基本思想是根据相关性大小把原始变量分组，使得同组内的变量之间相关性较高，而不同组的变量间的相关性则较低。每组变量代表一个基本结构，并用一个不可观测的综合变量表示，这个基本结构就称为公共因子。对于所研究的某一具体问题，原始变量可以分解成两部分之和的形式，一部分是少数几个不可测的所谓公共因子的线性函数，另一部分是与公共因子无关的特殊因子。

因子分析还可用于对变量或样品的分类处理。我们在得出因子的表达式之后，就可以把原始变量的数据代入表达式，得出因子得分值，根据因子得分在因子所构成的空间中把变量或样品点画出来，形象直观地达到分类的目的。

我们用F1、F2、…、Fm代表公因子，X1、X2、…、Xp代表可观测的随机变量,即显在变量,而这些因子是不可观测的潜在变量。

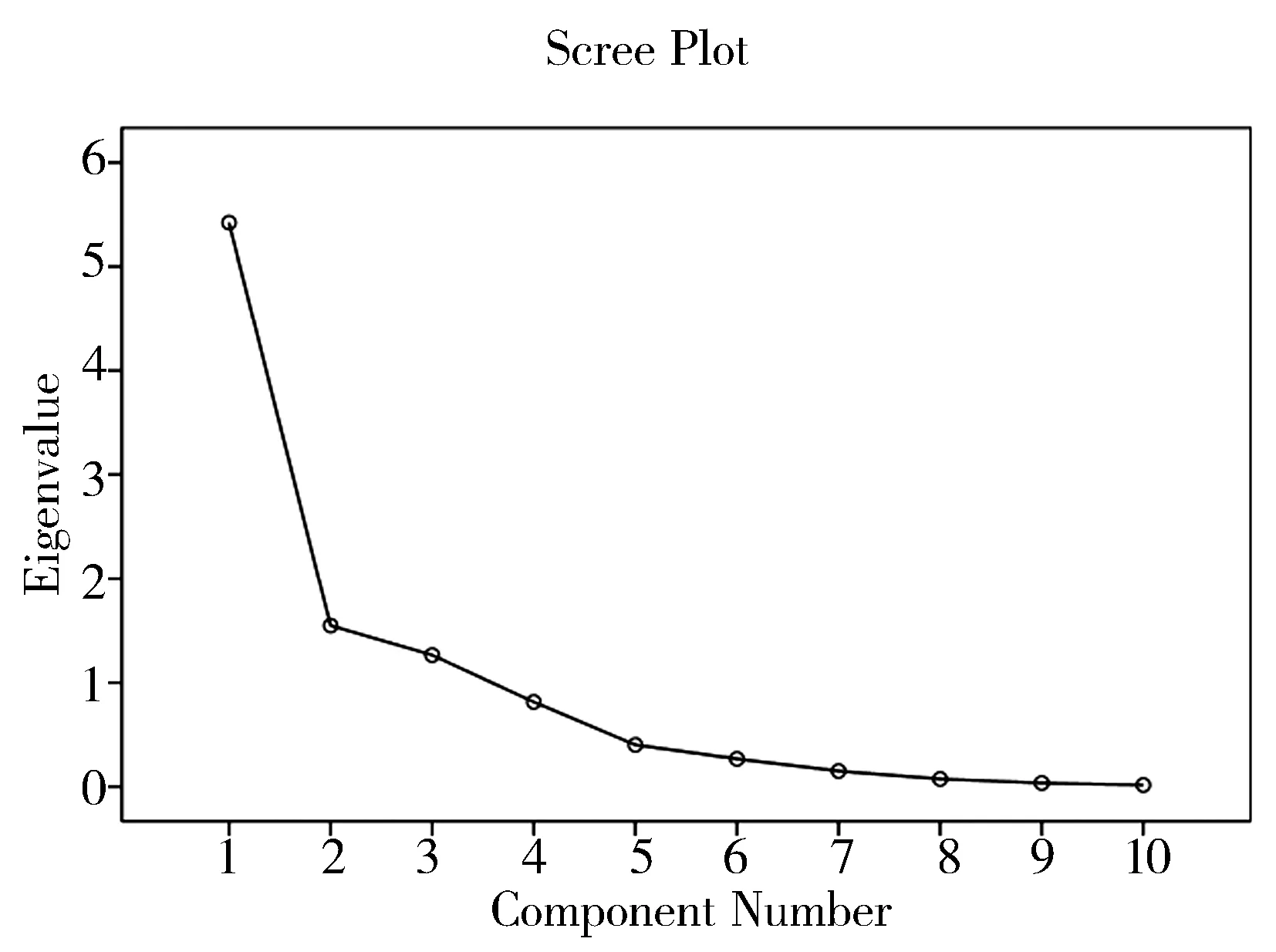
设X=(X1,X2,…,Xp)是P×1维的随机向量。F=(F1,F2,…,Fm)是m×1维的标准化的正交公共因子向量且m

在上述假定下,正交因子模型可以写成如下矩阵形式:

X = AF +ε

其中:A=(aij)称为因子载荷矩阵,aij表示第i个变量Xj在第j个因子Fj的载荷。因子载荷aij统计意义就是第i个变量与第j个公共因子相关系数即表示Xi依赖Fj的分量(比重)，据此,可以根据该列负荷中绝对值较大的负荷所对应的变量来说明这个因子的意义。模型中第i个特殊因子εi仅与第i个变量Xi有关系;而第i个公共因子Fi则与P个变量均有关系。

因子分析可以分为确定因子载荷、因子旋转及计算因子得分三个步骤。

(1)确定因子载荷或是根据样本数据确定出因子载荷矩阵。确定因子载荷矩阵的方法有很多，如主成分法、主轴因子法、最小二乘法、极大似然法、因子提取法等。这些方法求解因子载荷的出发点不同，所得的结果也不完全相同。

(2)因子旋转。为了对因子分析做出合理说明,即说明各个公共因子所代表的实际意义,可以通过旋转坐标轴使因子负荷在新的坐标系中能按列向0 或1 两极分化,以便得到一个更简单的易于解释的结构。因此,因子旋转的主要任务就是找到适当的变换矩阵T ,使旋转后的因子负荷阵尽可能具有简单结构。具体表现为:每一列上的负荷大部分应是很小的尽可能接近0 的值;每一行中只有少量的,最好是只有一个较大的负荷值;每两列中大负荷和小负荷的排列模式应该不同。

(3)因子得分。因子得分就是公共因子 F1,F2,…，Fm在每一个样品点上的得分。这需要我们给出用原始变量表示的公共因子线性表达式，这样的表达式一旦能够得到，就可以很方便地把原始变量的取值代入其中，求出各因子的得分值。

2.因子分析的结果

本文通过SPSS16.0软件对中原经济区29个省辖市2009年的截面数据进行分析，所有数据均来自各省统计年鉴及有关网站，其原始数据如表1所示。

表1 2009年29个城市原始数据

续表1 2009年29个城市原始数据

为消除原始数据量纲不同对分析的影响，首先应将原始数据进行标准化处理，使数据具有可比性。

其次，对标准化处理过的数据进行因子分析，按照特征根大于1的原则，选取3个公共因子。其特征根及累计贡献率、碎石图、因子载荷阵如表2、图1、表3所示。

由表2我们可以看出，前三个特征值较大，可以选取3个公共因子。其原始信息的特征值分别为5.423、1.549、1.265，每个公因子的贡献率分别为54.228%、15.494%、12.655%，三个特征值的累计贡献率达到了82.399%。而其旋转后的特征根分别为3.794、2.935、1.509，旋转后每个公因子的贡献率分别为37.943%、67.288%、15.089%。其中，第一个公因子对原始变量的解释能力最强，第二个公因子的解释能力次之。

表2 特征根及累计贡献率

图1 碎石图

表3 因子载荷矩阵

由于公共因子的因子载荷阵的实际意义不好解释，因此，我们对公共因子进行方差最大化正交旋转，得到旋转后的因子载荷阵，如表4所示。可以看出，旋转后的因子载荷阵发生了很大的变化。

表4 旋转后的因子载荷阵

表5 因子得分系数矩阵

由表4可以看出，变量X4(社会消费品零售总额)、X1(GDP)、X5(全社会固定资产投资总额)、X9(进出口总额)、X6(地方财政收入)在第一因子F1中有较大的正载荷，由于X4反映一定时期内人民物质文化生活水平的提高情况，X1、X6、X9反映一国或一地区的国力与财富，X5反映固定资产投资规模、速度、比例关系和使用方向，因而F1为反映城市规模及经济发展水平的公共因子；变量X2(人均GDP)、X7(农村居民人均纯收入)、X8(城镇居民人均可支配收入)在第二因子F2中有较大的正载荷，由于X4反映人民生活水平及富裕程度，X7、X8也在一定程度上反映城市和农村居民的生活水平，因此F2为反映城市富裕程度的公共因子；变量X3(GDP增长率)、X10(规模以上工业企业增加值)在第三因子F3中有较大的正载荷，由于X3、X10都是可以反映城市发展潜力的指标，因此命名F3为经济发展潜力的公共因子。

表6 因子得分及排名

由表5可以写出三个公共因子的因子得分函数：

F1=0.293×X1-0.174×X2-0.096×X3+0.325×X4+0.303×X5+0.15×X6-0.054×X7-0.13×X8+0.125×X9+0.05×X10

F2=-0.101×X1+0.445×X2-0.055×X3-0.158×X4-0.12×X5+0.121×X6+0.32×X7+0.371×X8+0.054×X9-0.058×X10

F3=0.025×X1-0.076×X2+0.618×X3+0.037×X4-0.086×X5-0.239×X6-0.061×X7+0.037×X8+0.184×X9+0.481×X10

由上述因子得分函数，我们可以得到每个城市的因子得分，从不同角度反映各市的实力。以三个公共因子对应的方差贡献率为权数基数，按各城市的综合分值，即以下列公式计算各城市的综合分值F，计算结果如表6所示。

从得分和排名可以看出，在中原经济区经济竞争力综合排名中，郑州市名列第一，邯郸市名列第二，排名前十的其他城市依次为洛阳市、聊城市、焦作市、菏泽市、安阳市、新乡市、南阳市、许昌市；而从经济发展规模来看，排名前十的依次是郑州市、邯郸市、洛阳市、南阳市、邢台市、周口市、菏泽市、运城市、商丘市、信阳市；从城市富裕程度来看，排名前十的依次是济源市、郑州市、晋城市、焦作市、长治市、鹤壁市、聊城市、许昌市、三门峡市、安阳市；从城市发展潜力来看，排名前十位的依次是聊城市、菏泽市、济源市、许昌市、洛阳市、新乡市、鹤壁市、邯郸市、阜阳市、亳州市。

三、结 论

通过运用多指标的综合评判方法对中原经济区29个城市的综合竞争力进行评价, 2009年29个城市在综合竞争力上有着巨大的差异,其中，郑州市综合得分为2.41，邯郸市为0.86，洛阳市、聊城市为0.80，焦作市为0.24，而综合得分最低的五个城市得分分别为驻马店市得分-0.44、淮北市得分-0.47、阜阳市得分-0.49、亳州市得分-0.52、宿州市得分-0.54，可见，中原经济区各城市经济发展不平衡, 城市之间经济竞争力差距较大。同时,结合对三个主要公因子得分进行分析,可以发现，济源市在城市富裕程度及发展潜力方面排名均位于前列，但是在城市规模水平上的得分排名却为最后一名，这可能与济源市人口较少且发展较晚有关，因此需在城市规模方面加大建设力度；鹤壁市、许昌市在城市富裕程度及发展潜力方面得分较城市规模的得分高，因此也应在城市规模方面有所改善，这样才能提升城市整体竞争力；长治市、晋城市、三门峡市等在富裕程度方面得分较高，而在城市规模及发展潜力方面的得分明显较低，使得综合得分下降，因此在城市发展战略上应该把发展经济规模及经济发展潜力放在首位；菏泽市、驻马店市、邯郸市、阜阳市的城市富裕水平得分相对较低，因此在城市发展战略上应该把居民生活水平的提高放在首位。总之，各个城市需在相对薄弱环节努力改进，提高各城市的整体竞争力，以提升中原经济区的综合实力。

[1]董小刚，王雪秋.多元统计方法在吉林省经济实力竞争力评价中的应用[J].长春工业大学学报，2005，(12)：66-68.

[2]刘亮亮.重庆经济发展现状及竞争力评价[J].牡丹江教育学院学报，2008，(4)：156-157，160.

[3]周泽炯.基于因子分析的县域经济竞争力研究——以安徽县域经济为例[J].经济体制改革，2010，(3)：150-153.

[4]张吉献，张艳玲.中原经济区各城市经济发展水平评价及发展对策[J].经济师，2009，(1)：279-280.

[5]申 强，侯云先.河南省区域综合竞争力评价分析[J].农业系统科学与综合研究，2010，(2)：34-39.

[6]何晓群.多元统计分析[M].北京：中国人民大学出版社，2010.

[7]于秀林，任雪松.多元统计分析[M].北京：中国统计出版社，2008.