信息不对称条件下基于TOC的供应链协调方法研究

冷凯君，王玉霞

（1.湖北经济学院物流与工程管理学院，湖北武汉430205；2.武汉理工大学华夏学院，湖北武汉430223）

信息不对称条件下基于TOC的供应链协调方法研究

冷凯君1，王玉霞2

（1.湖北经济学院物流与工程管理学院，湖北武汉430205；2.武汉理工大学华夏学院，湖北武汉430223）

市场日益激烈的竞争，使得企业只有与供应链上的合作伙伴齐心协力，加强合作，才能抓住市场上稍纵即逝的机遇，赢得更大的市场。保证供应链中有用信息的及时获得、快速传递是供应链得以协同工作的基础。结合约束理论（TOC）中的缓冲理论，形成以供应链下游企业向上游企业提供的日常共享信息准确度为激励条件的供应链协调策略，将能够促进信息不对称条件下供应链中各节点企业之间共享信息准确度的提升，进而提升供应链整体的收益水平。

信息不对称；供应链协调；约束理论

以高速增长和高速变化为特征的信息时代，充满了空前机遇与不确定性[1]。市场竞争日益激烈，新问题新情况层出不穷，企业只有与供应链上的合作伙伴齐心协力，加强合作，才能抓住市场上稍纵即逝的机遇，赢得更大的市场。企业竞争向供应链竞争的转化，迫使企业一方面集中一切力量，努力提高企业自身内部核心竞争力，另一方面通过加强与合作伙伴的交流与联系，协调工作，尽力提高供应链协同水平。保证供应链中有用信息的及时获得、快速传递、及时交流、正确使用是供应链得以协同工作的基础，供应链协同首先要解决如何保证供应链整体信息流通畅的问题。

但实际上供应链上的各个企业都会从自身利益最大化的原则出发进行决策，使得供应链企业之间存在信息不对称性，从而降低供应链的整体效益，所以企业开始关注供应链整体运作，进行供应链成员之间的协调，来提高整体供应链和各成员间的效益。而供应链上各企业利益的相对独立性仍不可避免产生不同程度的信息不对称性，从而造成供应链中信息的延误和扭曲，牛鞭效应是目前这一条件下常见的显性效应之一。解决这种供应链内部信息不对称的直接办法就是让供应链上的各企业采取协同合作的模式，共享私有信息。信息共享是指随着信息技术的发展，在供应链管理中的上游企业（或下游企业）利用EDI、ERP、CRM等信息技术基础设施实时掌握下游企业（上游企业）的生产、库存或者需求等信息，并以此为基础进行决策的过程。而随着电子商务的发展，供应链中的信息共享问题随着供应链的渠道变化造成了一系列新的问题，并使得在供应链的渠道多样化的过程中产生许多冲突。因此，如何以日常共享信息准确性作为供应链协调激励机制，以保证供应链系统效益最大化，成为本文研究的出发点。

一、问题描述及模型建立

1.问题描述

对于供应链中的共享信息，不同阶段的信息获得对产品生产安排、库存控制、配送计划等有着直接的影响[2]。综合现有的研究成果，研究得较多的跨组织共享信息包括：销售数据（包括POS数据）、订单信息、需求信息、预测需求、库存信息、成本信息以及库存补充决策。其他的还包括：生产能力[3]、生产进度安排[4]、产品计划[5]、交付时间安排[6]、运输信息[7]、预先到货信息[8]、供应信息[9]等。这种共享信息的分类方法是按信息服务职能对象的不同来进行划分的。

从供应链协同的角度出发，跨组织信息共享可根据企业边界分为：企业与上游，企业与下游，企业与其它供应链辅助成员单位[10]，企业与外部环境。企业间信息共享最初是为了弱化牛鞭效应而提出来的，对信息共享价值的研究早期主要偏重于研究从下游向上游传递的信息[11]，如POS数据、需求信息、订单信息、销售预测等。而对企业环境信息的共享，如政府信息、市场信息、行业信息等等，也是跨组织信息共享中已研究得比较深入的领域。但是上述信息分类并不能全面概括供应链中共享信息的特征，指导实践。对不同的供应链成员而言，共享信息的涉及面、涉及层次、信息粒度都是不一样的。本文考虑由生产商和分销商组成的单周期二阶段供应链模型，将生产商作为该供应链核心主体，以分销商与生产商日常共享信息准确度为主要参考指标，研究信息不对称条件下供应链协调问题。

与现实情况类似，在日常生产经营活动中，分销商往往从企业自我收益最大化角度出发，向生产商提供基于自身利益的共享信息，这些信息常常出现失真的情况，从而造成生产商过量生产及供应链整体的收益损失。而在一些特殊时段如节假日中，各分销商却也都需要生产商能够向其大量供货以保证销售，从而提升收益水平。因此，分销商日常共享信息的准确度能够成为生产商满足其大量需求时协调激励措施的依据和标准。根据TOC的理论，实际上分销环节已经越来越成为供应链系统中的“瓶颈”，即分销商环节的服务水平决定了供应链整体的有效产出，在目前金融危机的大背景下，生产商不得不以有限的资金投入生产，以分销商日常共享信息准确度为标准的供应链协调策略能够一方面控制生产商的生产计划安排，另一方面控制对于分销商环节的实际库存水平。日常共享信息的准确度成为了系统的信息“缓冲（Buffer）”，由它决定生产商对分销商需求满足的优先级。因而，此时可以利用基于TOC的供应链管理方法，以“信息缓冲”作为生产计划与控制的主线，达到长期的供应链协调。

2.模型建立

本文中所建立的供应链模型是以生产商与分销商为主体的单周期供应链系统，其中生产商拥有M个生产厂生产不同类型的产品，且供应链中有N个主要的大型分销商，其供应链整体结构如图1所示。

在时段性高需求的条件下，分销商为了应对市场的需求往往都会希望能够尽量多地增加自身的产品库存水平以达到相应的服务水平，从而获得更多的有效产出，因此会在需求高峰来临的销售周期之前，以此为基础向生产商提供相应的产品需求信息，生产商则以分销商产品需求信息为参考，在能够投入生产资金受限，并且产能一定的条件下进行时段性高需求条件下的生产，此时各生产厂的生产都会是以最大产能投入生产，生产商再根据供应链整体的协调策略决定具体由哪些生产厂为哪些分销商生产出产品后应用VMI库存体系对分销商进行供应补货。

在具体的协调过程中，生产商将先根据信息缓冲管理对各分销商供享信息水平分类，并得到不同分销商相应的优先级，再结合生产商总体产能确定在供应链协调中各分销商的最低保证产品数量，之后在这一最低保证数量的约束下再根据各种实际情况进行生产。

在建立具体的模型之前，我们首先做如下的符号设定与相应的假设：

令i=1，2，…，t，…，r，…，w，…M表示各生产不同类型产品的生产厂，但共同隶属于同一制造企业，为能够更清晰地用模型进行说明，我们假设该供应链仅生产A，B，C三种不同类型的产品，

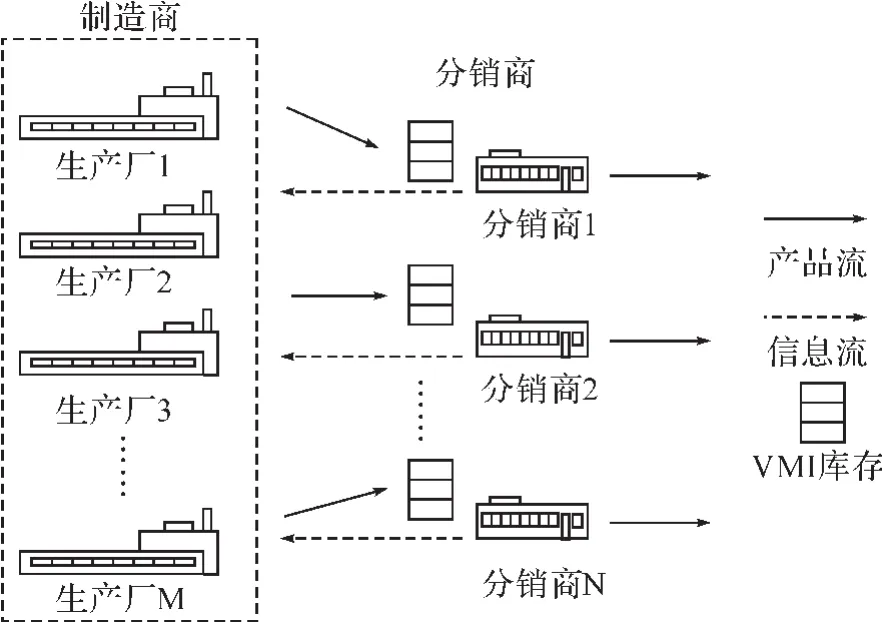
（图1） 单周期供应链系统整体结构图

其中：[1，t]为 A 型产品生产厂；[t+1，r]为 B 型产品生产厂；[r+1，w]为 C 型产品生产厂；j=1，2，…，N表示有着各自不同信息准确度的分销商；Wi表示各生产厂时段性应急生产时可投入的最大产能；σ表示根据TOC理论中的缓冲设置所设定的最低需求满足弹性系数，即为保证各分销商基本供给需求量所设定的生产量占总可用产能百分比；Dj表示各分销商在销售周期到来之前向生产商提出的产品最低需求数量；Uj表示由基于TOC的信息缓冲管理策略得出的各分销商相应的权重系数；pij表示某一生产厂为某一分销商每时段性应急生产一个批次件产品可满足该分销商在该时段应对高需求量的概率，这一参数值可由各分销商在各时段性需求条件下的总体销售纪录进行相关统计分析后得到，由于作为供应链“瓶颈环节”的分销商的服务水平决定了供应链整体的有效产出，因此这一变量也是供应链协调目标函数中的重要参数；cij表示某一生产厂根据不同分销需求，每为其进行时段性应急生产一个批次其所需要产品而必须投入的单位成本，其中包括原材料的应急采购费，应急生产人力成本，设备检修成本，运输成本等各项成本费用；xij表示某一生产厂商根据供应链整体协调策略为某一分销商生产的批次数，这也是在这一供应链协调问题中的主要决策变量；F表示在时段性应急生产期间生产投入可用资金总量；β1表示根据分销商产品基本需求信息，生产商对A型产品生产总投入约束比例；β2表示根据分销商产品基本需求信息，生产商对B型产品生产总投入约束比例；β3表示根据分销商产品基本需求信息，生产商对C型产品生产总投入约束比例；

在以上设定的基础上，我们开始建立时段性高需求条件下的短生命周期产品供应链产销协调优化模型。

本文所研究的供应链协调的首要目标是通过对各生产厂生产计划与控制的决策使各分销商能够满足时段性高需求的概率达到最大，同时也使得供应链整体收益最大，因此供应链协调的目标函数为：

同时，供应链协调决策过程中最大的约束来自于可投入应急生产的资金数量，各生产厂商所受资金约束亦即目标函数的约束表示如下：

其中A型产品生产厂会受到时段性生产可投入资金限制，其约束为

B型产品生产厂受到时段性生产可投入资金的限制，其约束为

C型产品生产厂受到时段性生产可投入资金的限制，其约束为

整个供应链协调的过程在根据基于TOC的协调策略满足各分销商为应对时段性需求高峰的最低产品需求量时，其约束为：

而如果以需求量大小为协调决策目标时，则优先满足需求量最大的分销商，并依次满足，直至产能用尽，在此种条件下的约束为：

同时在时段性应急生产的过程中，各不同类型产品生产厂也会受到其自身最大可用产能的约束：

对∀i=1，2，…N，∀j=1，2，…，M，xij≥0 且都为整数。

模型（1）实际上类似于一个WTA（Weapon Target Allocation）武器-目标分配调度问题，而它也是现代战争中一个十分重要的问题，但是由于其解空间是随M（武器总数）和N（目标总数）的增加而呈指数级增加，因而该模型实际上是一个多参数、多约束NP问题。这类组合优化的资源分配问题带有大量的局部极值点，往往是不可微的、不连续的、有约束条件和高度非线性[12]。尽管目前对这一问题的求解规模与精度方面都有了较大程度的提高，但仍然存在一定的问题：如采用神经网络算法有时得不到稳定解，采用遗传算法又存在迭代时间长、容易陷入局部最优解等问题，因此本文根据所要解决问题的实际情况，在传统遗传算法的基础上进行了诸多改进，使得求解结果在充分满足约束条件的前提下，拥有了较好的求解速度和求解稳健性。

二、模型求解过程

根据本文所建立模型的具体情况，在应用基于遗传算法的具体模型求解过程中，由于受到应急生产过程中各种成本、产能的约束，因此，必须对初始产生的种群以及后续生成的子代新种群中的个体进行相应的检验，并根据不同的结果进行相应的调整设置。在种群质量检验调整算法中主要包括三个模块，Module1是对染色体的行向量进行约束调整的模块，其设置的目的是使各个生产商应急生产的批次数不超过其产能的约束，其中Module2为对染色体的列向量进行约束调整的模块，其设置的目的是使各生产厂商应急性生产的批次能满足分销商时段性高需求的基本要求，其中；Module3 则是在Module1，Module2进行完相应的调整后再对染色体整体进行的相应调整，其中由命令i′=rand{Ik}，j′=rand（1，N），flag=0 将染色体中代表不同产品生产类型的厂商分开，并按照总可能生产投入资金的占有比例约束进行调整，在计算的过程中命令。种群检验调整算法整体流程如图2所示。

遗传算法遵循的是自然界优胜劣汰的原则，在进化搜索的过程中基本不用外部信息，而是用适应度值来表示个体的优劣，针对本文所要解决的问题，适应度函数的设计也是结合了所要求解问题本身的要求而制定的。在保证是最大化问题和非负性的前提下，一般适应度函数都是由目标函数加以变换而得，而根据模型（1）所要解决的问题，在本文的适应度函数设计中将待求解优化问题的目标函数的核心部分取作适应度函数，并且目标函数为求解最大化问题，则适应度函数为：

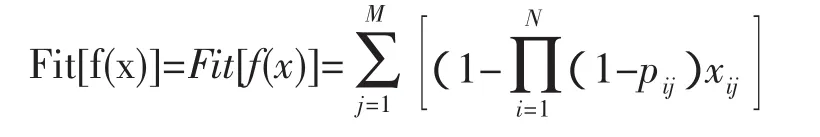
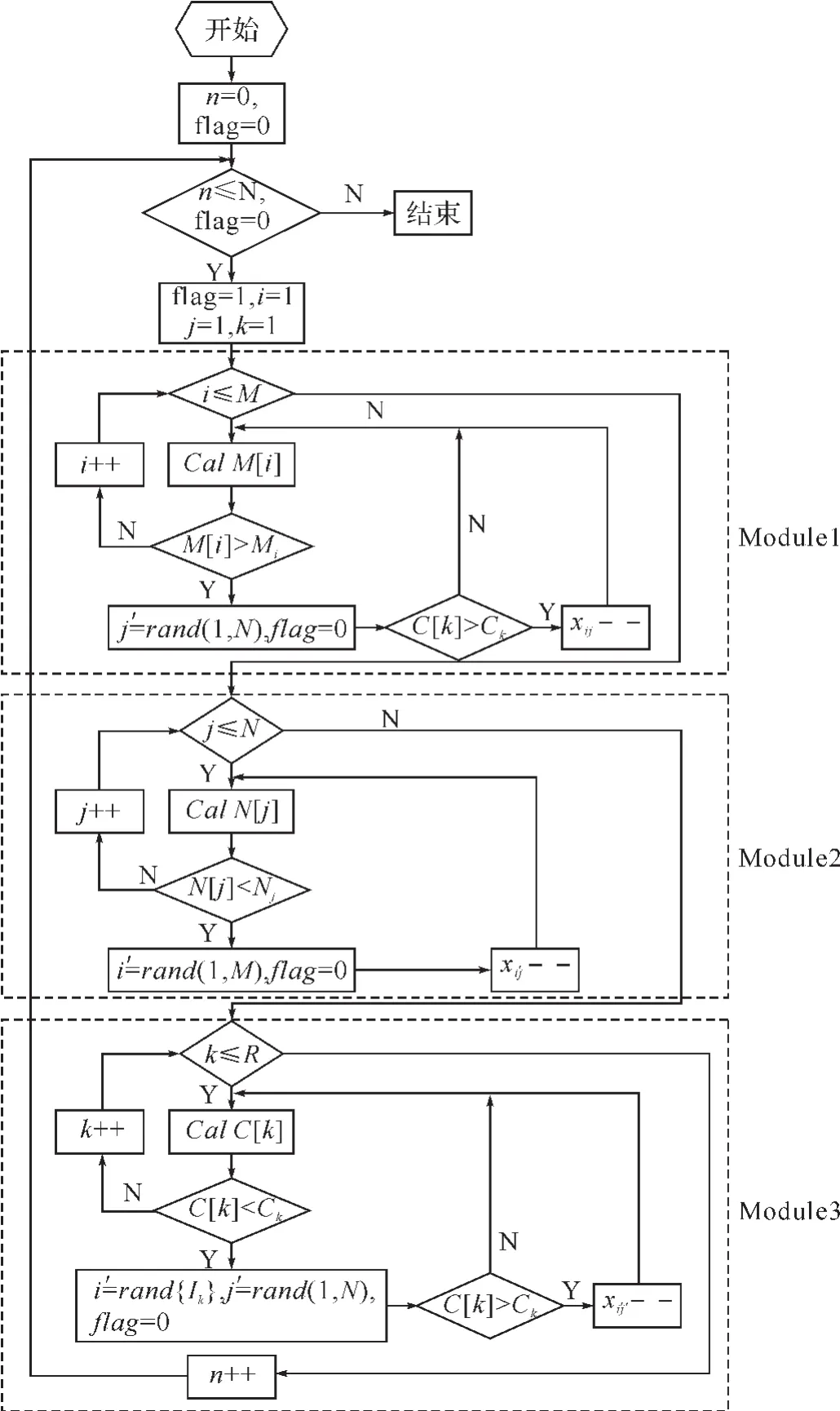
（图2） 种群质量检验调整算法设置流程

另外，我们在考虑适应度函数的设计中，也考虑了其尺度问题，在本文遗传算法的设置中，由于染色体及适应度函数的相应设置，在算法实现过程中不会出现欺骗问题。算法具体实现步骤与常规遗传算法步骤过程类似。

三、算例分析

在算例中，初始设定为由拥有15间工厂的生产商和4家大型分销商（S1-S4）组成的供应链系统，不失一般性，仍然令供应链向市场提供A，B，C三种不同型号的产品，其中生产A产品的工厂有7间，生产B产品的工厂为2间，生产C产品的工厂为6间。尽管面对时段性的需求高峰，但生产商将由于受到资金流的限制，总可投入生产的资金为F=7500000元，同时根据三种产品的市场需求，对三类产品生产可投入资金限定的基本比例为别为β1=55%，β2=15%，β3=25%。

作为供应链“瓶颈环节”的分销商的服务水平决定了供应链整体的有效产出，因此首先我们给定表示某一生产厂为某一分销商每时段性应急生产一个批次产品可满足该分销商在该季成功应对高需求量的概率的参数，这一参数的具体数值可由各分销商历史销售纪录进行相关统计分析后得到，如表1所示：

（表1） 生产商时段性应急生产满足分销商需求概率

分销商在销售旺季到来之前会向生产商提出相应的需求信息，即各分销商相应的订货量，但各分销商也具有不同的信息水平，而根据本文中所提出的“信息缓冲管理”的思想，生产商将这些分销商按其信息水平赋予不同的权重，并由不同的分销商权重生产商根据自身产能所确定的对其最低需求满足量也会各不相同，在本算例中，我们将最低需求满足弹性系数设定为σ=0.7。此外，不同生产厂根据分销商对产品的相应需求应急生产一批次产品的成本也各不相同，具体参数设定如表2所示（其中成本单位为1000000元，产能单位为批次）：

下面我们将应用本文中所设计的遗传算法及具体步骤，针对模型（1），结合上述参数设定，以基于TOC的协调方法进行相应的模型求解和计算，在验证算法的有效性的同时进一步研究该方法的适用性。无论何种方法，由于模型1的NP完全性，应用遗传算法求出相应的结果都具有一定波动性，因此我们将求解出结果的最优值列出，如表3所示，同时解的波动情况如图3所示：

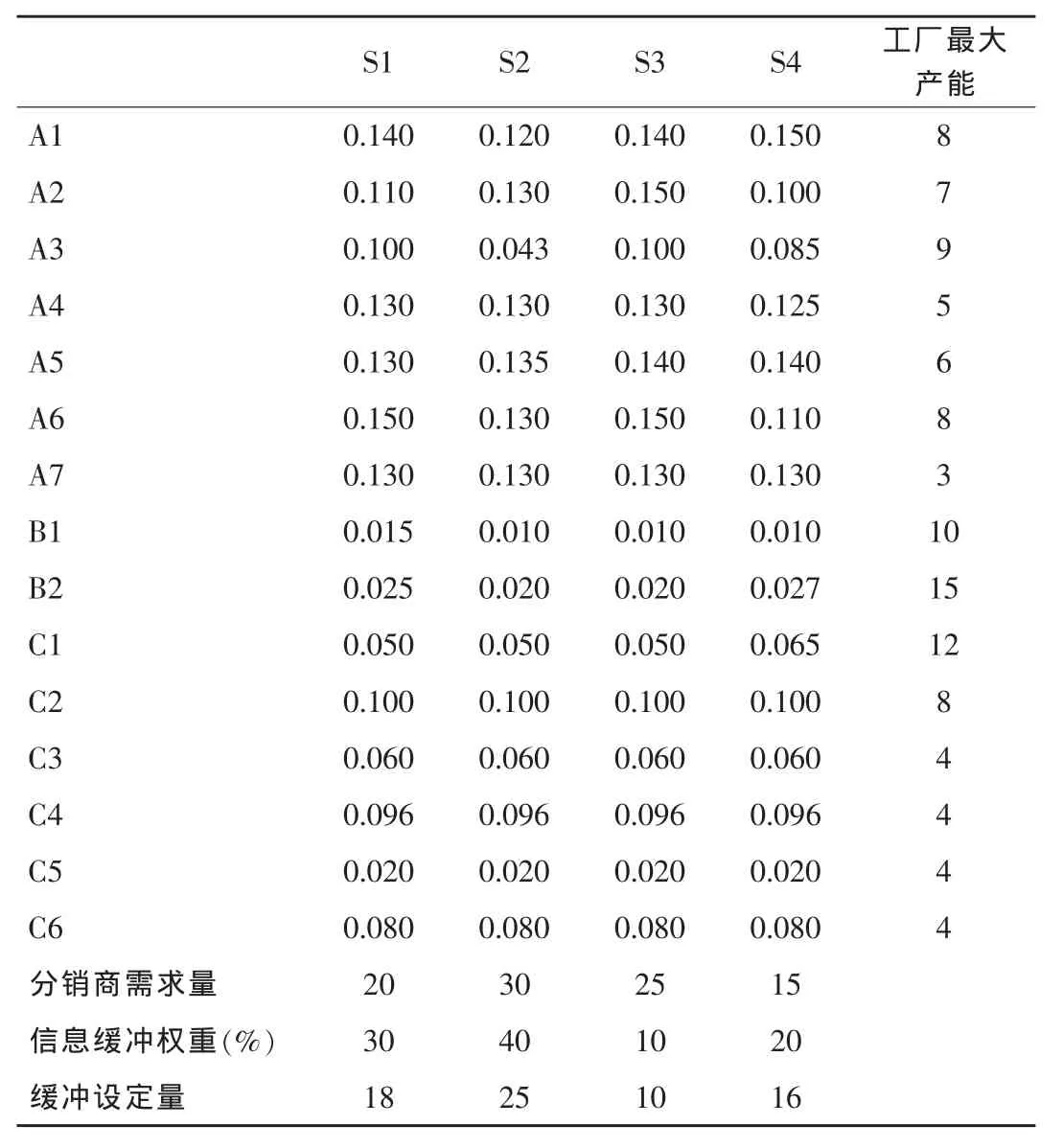
（表2） 时段性应急生产参数设定

（表3） 基于TOC协调方法的最优解

从图3中的表现我们可以看出，采用基于TOC的协调方法，在应用本文所提出的遗传算法求解时，适应度函数值的波动幅度比较小，因此证明了算法在解决这类问题时的有效性。同时，基于TOC的协调方法在求解的过程中的波动幅度相对于基于数量的协调方法而言更为稳定，因此求解得出的最优结果也更为稳健。

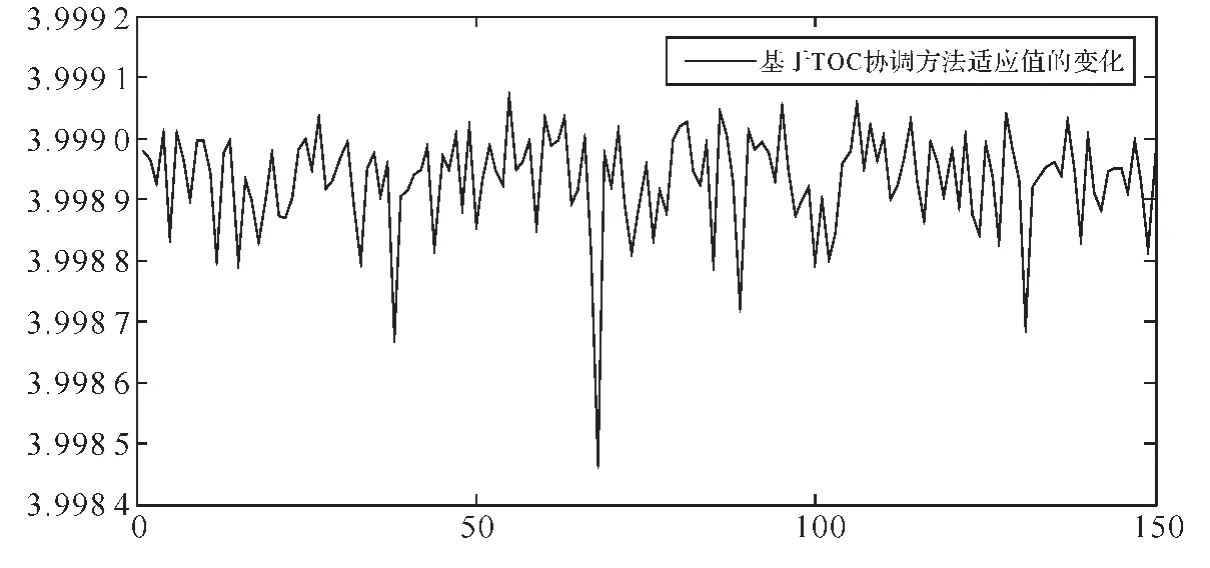
（图3） 基于TOC协调方法进行求解时适应值的变化过程

此外，根据表3我们可以看出，基于TOC协调方法所得出的适应度函数最优值和有效产出值较高。因此也进一步说明了在本文所研究的供应链协调问题中，在处于时段性需求高峰和资金限制条件下，基于TOC协调方法更有优势。

四、结论与展望

本文研究了由拥有多家生产厂的生产企业和多家分销商所组成的单周期供应链系统中，在出现时段性需求高峰，同时生产商又受到可投入生产资金约束限制的条件下，如何运用基于TOC体系的方法进行相应的产销协调以保证供应链整体有效产出最大的问题。而由于建立起的系统模型实际是一个NP完全问题，因此在本文中选择使用遗传算法对模型求解，并结合所要解决的实际问题对遗传算法进行了相应改进，通过算例在验证了算法有效性的同时也进一步验证了相关理论。同时，在进一步的研究中，可以将该模型应用于多周期多层级的供应链结构中，在算法的改进上亦存在更多的选择，这些都将成为进一步研究与改进的方向。

[1]周伯生，樊东平.零时间：21 世纪企业的概念构架[J].中国机械工程，2001，（2）.

[2]U.W.Thonemann.Improving supply-chain performance by sharing advance demand information [J].European Journal of Operational Research，2002，（1）.

[3]H.L.Lee，K.C.So，C.S.Tang.The value of information sharing in a two-level supply chain[J].Management Science，2000，（5）.

[4]Y.Li，G.W.Tan.Information sharing in a supply chain with dynamic consumer demand pattern[C].Proceedings of the 37th Hawaii International Conference on System Sciences，Hawaii.USA，IEEE Computer Society Press，2004.

[5]郑欣，张诚，凌鸿.评估供货量信息的共享在供应链管理中的价值[J].中国管理科学，2003，（3）.

[6]F.Chen.Information sharing and supply chain coordination[J].Handbooks in Operations Research and Management Science，2003，（11）.

[7]陈宝国，卢山.信息不对称条件下企业物流外包过程的风险和防范[J].中国安全科学学报，2004，（1）.

[8]G.P.Cachon，M.Fisher.Supply chain inventory management and the value of shared information[J].Management Science，2000，（8）.

[9]吴轩洪，陈萨.网际时代供应链信息共享的有效性分析[J].重庆大学学报，2001，（8）.

[10]J.Liang，S.Q.Cai.Information Asymmetry and Correlative Principal-Agent in Logistics outsourcing[J].Advances in Systems Science and Applications，2005，（3）.

[11]刘志学，许泽勇.基于非对称信息理论的第三方物流合作博弈分析[J].中国管理科学，2003，（5）.

[12]董彦非，冯惊雷，张恒喜.多机空战仿真协同战术决策方法[J].系统仿真学报，2002，（6）.

F274；F224.3

A

1001－4799（2012）01－0088－06

2011-01-05

国家自然科学基金资助项目：71101047；湖北省教育厅青年基金资助项目：Q 20112201；湖北物流发展研究中心资助项目：2011 A 12；湖北省教育厅人文社会科学研究资助项目：2011JYTY066

冷凯君（1981-），男，湖南浏阳人，湖北经济学院物流与工程管理学院讲师，管理学博士；王玉霞（1980-），女，河南周口人，武汉理工大学华夏学院讲师。

朱建堂］