基于关联维数的神经元动作电位特征提取与分类研究

詹跃荣 范影乐* 杨文伟 杨 勇 李 轶（杭州电子科技大学自动化学院，杭州 3008）

2（杭州电子科技大学生物医学工程与仪器研究所，杭州 310018）

引言

动作电位（spike）是神经元所接收、分析和传递的信号载体，是神经元网络活动的基本表现形式。近年来，随着植入式多电极阵列（multi-electrode arrays，MEA）记录技术的发展，用细胞外神经元动作电位进行记录和分析已成为神经生理学的重要研究手段。然而，MEA中单个电极所采集到的信号往往是电极附近多个神经元发放的动作电位和大量神经系统内外噪声的叠加。因此，如何有效地对spike信号进行检测和模式分类，是研究神经元动作电位序列（spike train）信息特征的重要工作，并可为后续神经元信息编码研究奠定基础。

动作电位分类过程主要包括信号检测、特征提取、模式分类三部分。针对动作电位的特征提取，国内外学者提出了主成分分析法（principal component analysis， PCA）［1］、小 波 分 析（wavelet analysis，WA）［2－3］和基于相空间（phase space）的特征提取［4］等多种分析方法。目前，主要的研究方法为主成分分析法和小波分析的方法。其中，PCA方法通过样本协方差矩阵求取主要特征值，但由于spike信号具有一定的非线性时变特性，因此 PCA可能无法表征spike信号的完整信息。基于小波分析的方法通过对spike信号进行多层分解，在时频域上对spike信号特征进行动态描述。但是，此方法得到的信号信息是由小波系数整体合并来反映的，而在实际分类中小波系数是单独作用的，很多有用的波形信息可能被丢失。在模式分类阶段，通过对特征向量的分析处理，利用不同的数据特性进行统计聚类。目前，大多数的神经元动作电位分类方法是基于动作电位的波形差异，包括模板匹配［5］，以及基于神经元放电特性的动作电位分类方法［6］。由于神经元的电生理活动存在相互影响，且反映神经编码特性的放电时间间隔分布较为复杂，因此使用上述方法具有较大的局限性。

神经元电生理活动通常被视为处于一个不稳定的混沌状态［7］，而描述混沌机制的一种有效手段就是分形理论；关联维数是分形维数的一种，它作为混沌系统的重要特征，反映了系统的复杂程度，可用于刻画神经元动作电位的特征信息。本研究提出应用关联维数，对动作电位的波形特征进行无监督自动提取。考虑到K均值（K-means）方法具有较好的收敛性，并能够在一定程度上解决聚类叠加的问题，所以采用这种方法进行特征聚类，最终实现动作电位的无监督分类。

1 相空间重构及其相关参数的确定

根据嵌入理论，单个时间序列可以重构系统相空间，且重构的系统相空间与原始系统拓扑等价。如果嵌入维数m≥2d+1（d为动力系统维数），则这个动力系统的吸引子空间几何结构就会被完全打开，嵌入相空间就可以把有规律的轨迹恢复出来。

设植入式多电极阵列某通道采集到一个spike序列，即

式中，xi为采样值，n为采样点个数。

选择合适的嵌入延迟时间τ和嵌入维m，得到一个m维的嵌入相空间，相空间中的向量可表示为

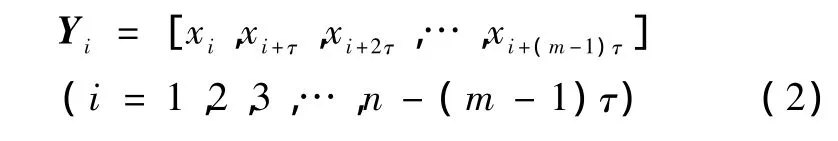
令N=n－（m－1）τ，则重构的多维相空间可表示为

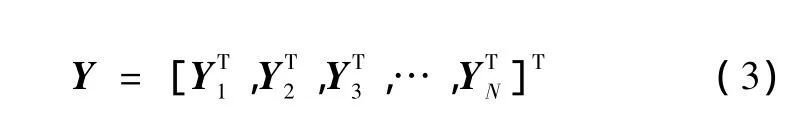
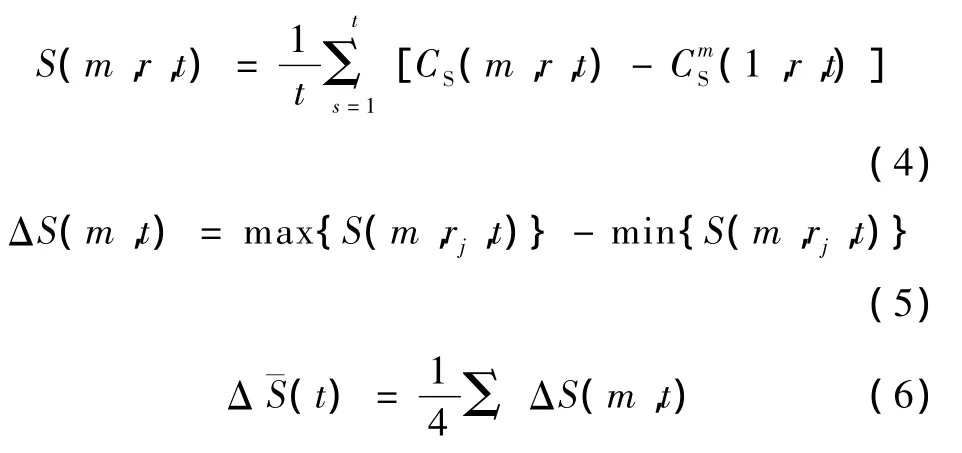
估计延迟时间τ可通过式（4）～式（6）来确定，有式中，rj=jσ/2，σ为给定时间序列的标准差，C（m，r，t） 为关联积分。

在嵌入维数m的求取过程中，参考伪最近邻方法（FNN）的思想进行计算，有

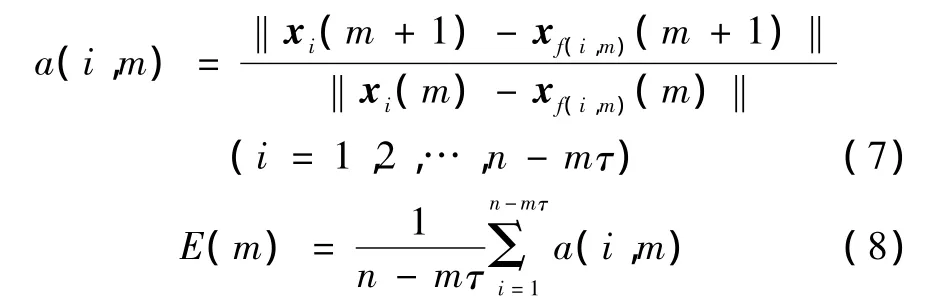
式中，xi（m）为m维相空间中的第i个向量，f（i，m）为第i个向量的最近邻点的下标。

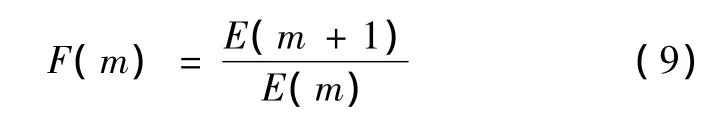
当m大于某个m0时，若F（m）不再明显地发生变化并接近于1，则此时m0+1为最小嵌入维数［9］。

2 关联维数

关联维数以相关性定义，当系统状态随时间变化时，状态变量前后的相关性可以用来表征信号是否有确定的规律及其程度，所以关联维数反映了系统的几何自相似特性。在确定嵌入延迟时间τ和嵌入维数m后，在重构相空间中利用关联积分计算关联维数。

设Yi是重构的相空间中第i个向量，计算其余N－1个向量与Yi的距离，采用最大模表示Euclidean距离，即

rij=d（Yi－Yj）=

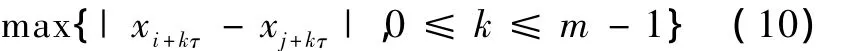
定义关联积分，有

3 关联维数提取神经元动作电位特征

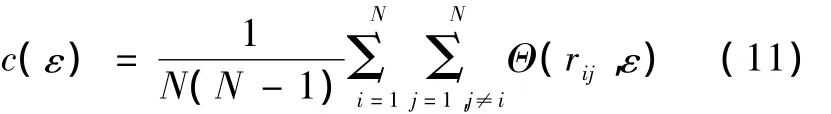
式中，N为相空间代表点（状态矢量）的数目，ε为相空间中给定超小球的半径，Θ（·）为 Heaviside函数。

当ε充分小时，关联维数可定义为

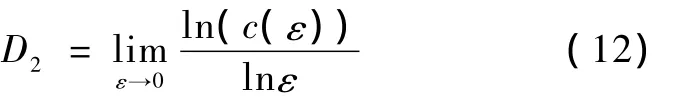
在实际计算关联维数时，利用 ln（c?（ε））～lnε曲线，通过线性拟合可得到D2。用高斯函数u（rij，ε）代替阶跃函数，以改善 ln（c（ε））～lnε关系的光滑性。高斯函数定义为

选取一组仿真的典型spike数据，如图1所示。仿真数据来源于加州理工大学Andersen实验室提供的C_Easy1_noise01数据，其噪声水平为0.10，采样频率为24 kHz，每个动作电位的时间长度为8/3 ms。图2（a）表示 C_Easy1_noise01数据中3类不同的spike信号，每个子图为20个同类spike信号叠加在一起，这些同类spike信号在波形上具有类似性，因此状态变量的前后相关性应具有类似性。图2（b）表示对应的3类 spike信号的 ln（c（ε））～lnε曲线，其中同类 spike信号的ln（c（ε））～lnε曲线相似度极高，则通过线性拟合得到的关联维数也是十分接近的；但不同类型 spike信号的 ln（c（ε））～lnε曲线存在较大差异，有利于区分不同类型的 spike信号。这也表明，利用关联维数对动作电位模式分类是可行的。

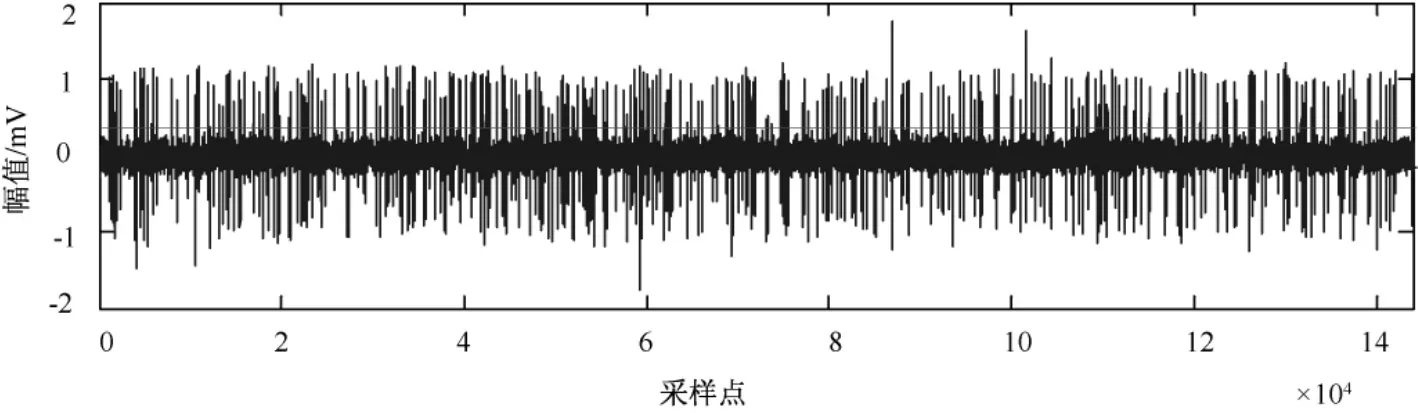
图1 含噪spike序列Fig.1 Spike train with noise

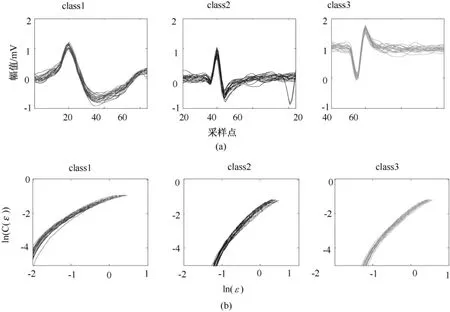
图2 3类不同spike信号及其相应的ln（c（ε））～lnε曲线。（a）3类不同spike信号波形；（b）3类不同spike对应的 ln（c（ε））～lnε曲线Fig.2 Three different types of spike signals and corresponding curve of ln（c（ε））～ lnε.（a）three different types of spike signals；（b）ln（c（ε））～ lnεcurve of three types

在求取关联维数时，首先对采集到的 spike信号序列进行相空间重构。以图2中的3类spike信号为例，计算确定嵌入延迟时间τ=2，嵌入维数m=12。如图3所示，当嵌入维数m＞11时，F（m）不再明显发生变化并且接近于1，取最小嵌入维数m=12。

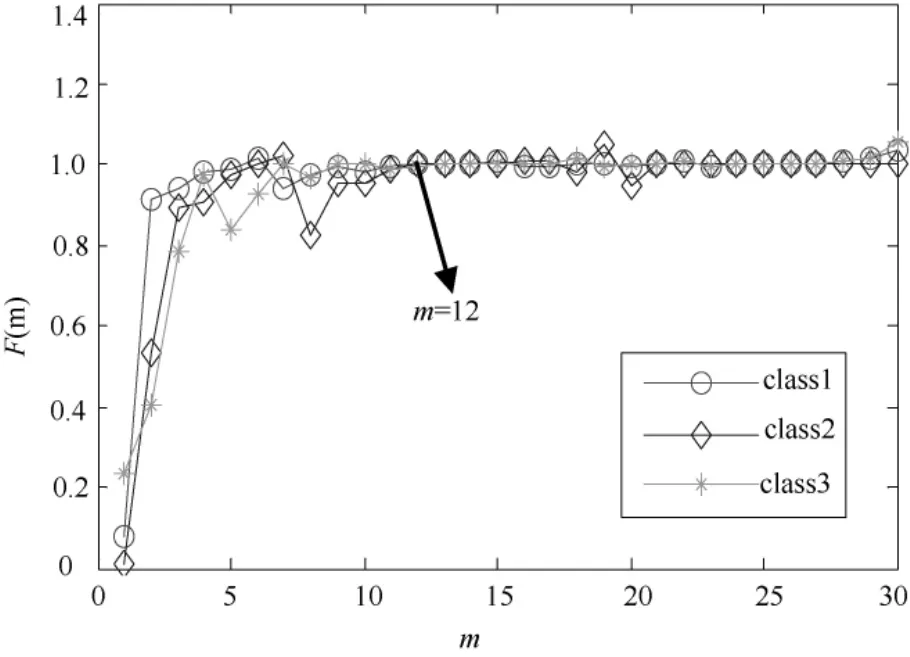
图3 嵌入维数选择Fig.3 The diagram of choosing embedding dimension

图4为来源于上述3类spike信号的叠加，3类spike信号总数为2 990个。图5为对应3类 spike信号的关联维数分布，可看出3类spike信号的关联维数分布具有明显的分层现象。本研究模式分类算法采用K均值方法，对计算得到的spike关联维数实现无监督分类。

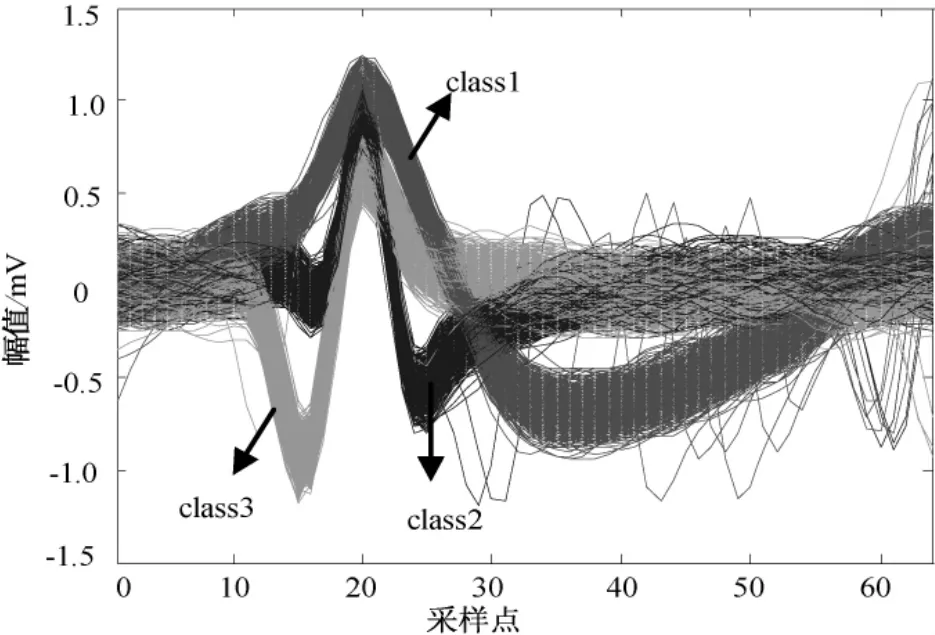
图4 3类spike信号叠加Fig.4 The superposition of three different types of spike

动作电位分类算法有下列步骤。

步骤1：采用阈值法，检测隐藏在原始信号中的spike 信号 spi（i=1，2，3，…，n），阈值 Thr确定为［3］

图5 3类spike信号关联维数分布Fig.5 The distribution of correlation dimension of three different types of spike

式中：k为经验值，视噪声而定；E为原始信号经巴特沃斯带通滤波器（带宽为300～6 000Hz）后的信号，median为取中值。

步骤2：确定嵌入延迟时间τ和合适的嵌入维数m。

步骤3：计算每个spike所对应的关联维数。

步骤4：利用不同类spike的关联维数具有明显的分层分布现象，通过K均值实现spike信号的无监督分类。

4 数据说明

本算法的验证数据分为仿真数据和实验记录数据两部分。

仿真数据来源于加州理工大学Andersen实验室提供的spike含噪仿真数据，每段神经元spike信号采样时长为6 000 ms，采样频率为24 kHz，每个spike片段设置为8/3 ms，即64个采样点。仿真数据提供每个spike信号所属的神经元类别，为本算法的准确率性能评价提供了参照标准。

实验记录数据来源于本实验室采集到的大鼠初级运动皮层神经元电信号。通过手术将16通道的多电极阵列（MEA）植入大鼠的初级运动皮层，然后在术后第三天采集大鼠该皮层神经元的自发放电序列；MEA采集到的spike模拟信号经前置放大器（PreAmp）初步放大后，进入Plexon多通道数据采集处理器（MAP），在 MAP提供的40 kHz采样频率下转换为spike数字信号，并在PC机SortClient信号采集软件配合下，记录微电极阵列各通道采集的spike序列数据。实验中 MAP系统的增益设置为1 000，采样时长为8 000 ms，每个 spike片段时长为1.4 ms，即54个采样点。大鼠初级运动皮层神经元spike数据采集系统如图6所示。

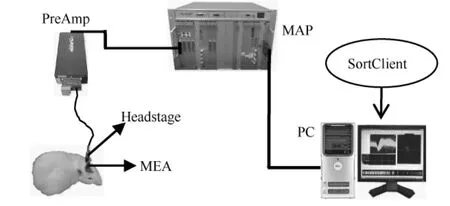
图6 大鼠初级运动皮层神经元spike数据采集系统Fig.6 Spike data acquisition system of primary motor cortex in rats

5 结果及其分析

5.1 仿真数据结果及分析

为了验证关联维数对spike信号分类的普遍有效性，笔者随机选择4组仿真spike信号进行实验，每组仿真数据为3类不同数目的spike信号叠加，分类结果统计如表1所示。其中，准确个数定义为实验中每一类正确分类的 spike信号个数，错分个数定义为错分到该类但实属它类的spike信号个数，准确率定义为每类正确分类之和与待分类spike信号的总数之百分比，1#、2#、3#分别表示每组数据中3类不同的spike信号，M和SD分别定义为每组数据3类不同spike信号分类准确率的平均值和标准差。从表1中可知，利用关联维数对spike信号模式进行分类，准确率达到95％以上，每类只有小部分出现了错分。如前所述，由于受微电极阵列技术的限制，植入式多电极阵列中的各个电极通常并不能准确定位到单个神经元。采集的信号一般来源于神经细胞间质，是电极周围多个神经元电活动的综合反映；信号记录将不可避免地受到外界刺激扰动和周围神经细胞的相互电磁等外干扰的影响，以及细胞体膜参数、放电阈值的随机起伏变化等因素引起的内噪声影响。因此，对于部分数据，关联维数方法也出现了错分，但从表1可看出关联维数能有效刻画不同类spike信号的特征，并可达到较为满意的分类效果。

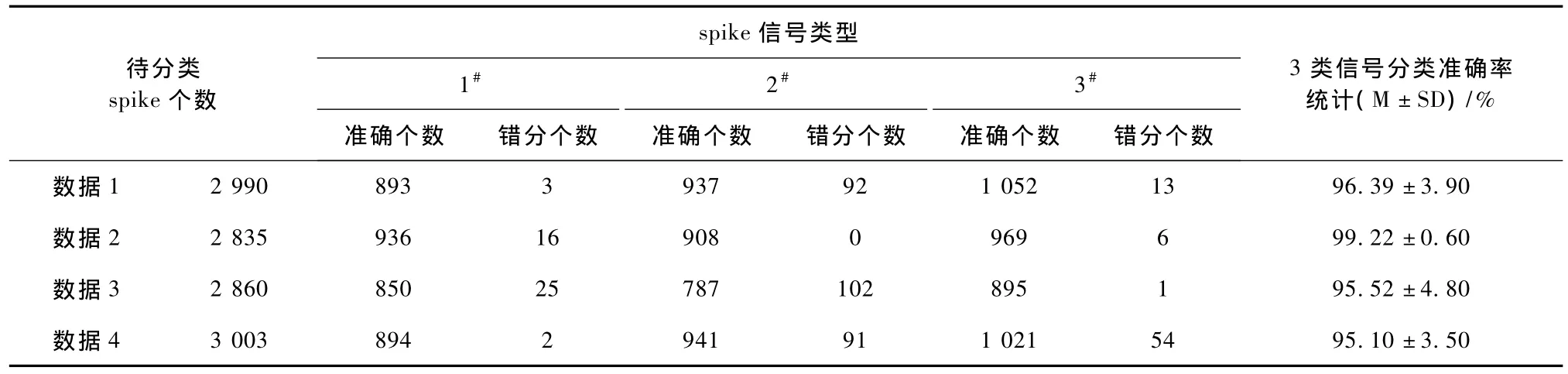
表1 4组仿真信号的spike分类结果统计Tab.1 Clustering result of four groups of simulated spikes

表2给出了分别采用PCA方法、小波分析方法和基于关联维数方法的分类结果对比，其中PCA方法是利用matlab统计工具箱里的princomp函数来提取 spike的特征信息，而小波分析方法是利用matlab小波分析工具箱里的wavedec函数进行小波分解，进而提取spike的特征信息。表2中的1#、2#、3#分别表示每组数据中3类不同的spike信号，M和SD分别定义为每组数据3类不同spike信号分类准确率的平均值和标准差，其中类间准确率是每一组数据中一类spike聚类正确率。从表2中每组数据分类的总准确率可得出，基于关联维数的分类方法总体优于PCA分类方法。因类间准确率反映了每类spike信号的分类效果，根据表2的类间准确率可得出，除个别spike信号PCA方法的分类效果好于基于关联维数方法的分类效果外，大部分类间准确率显示，基于关联维数分类方法优于PCA分类方法。表2展示针对不同的数据组，小波分析方法和基于关联维数的分类方法各有长处，总体分类性能大体相当。但小波分析方法针对不同的数据，需要选择合适的小波基来分析，如果面对大数据量时，如何选择合适的小波基将耗费大量时间，影响分类的效率，因此基于关联维数的分类方法在可实现性方面要优于小波分析方法。

5.2 实验记录数据结果及分析

微电极阵列第11通道采集的大鼠初级运动皮层神经元动作电位序列数据，如图7所示。经阈值检测和滤波后，spike信号的叠加如图8所示。在对spike信号序列重构相空间时，取嵌入延迟时间τ=2，取嵌入维数 m=16。

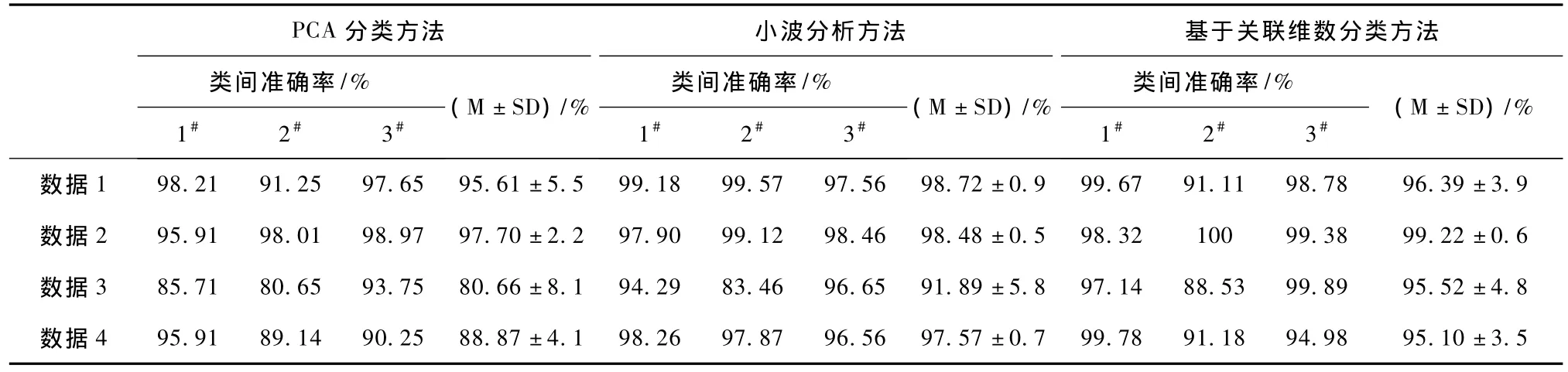
表2 仿真数据的不同分类方法的结果Tab.2 Clustering result of simulated data wi th different sorting techniques

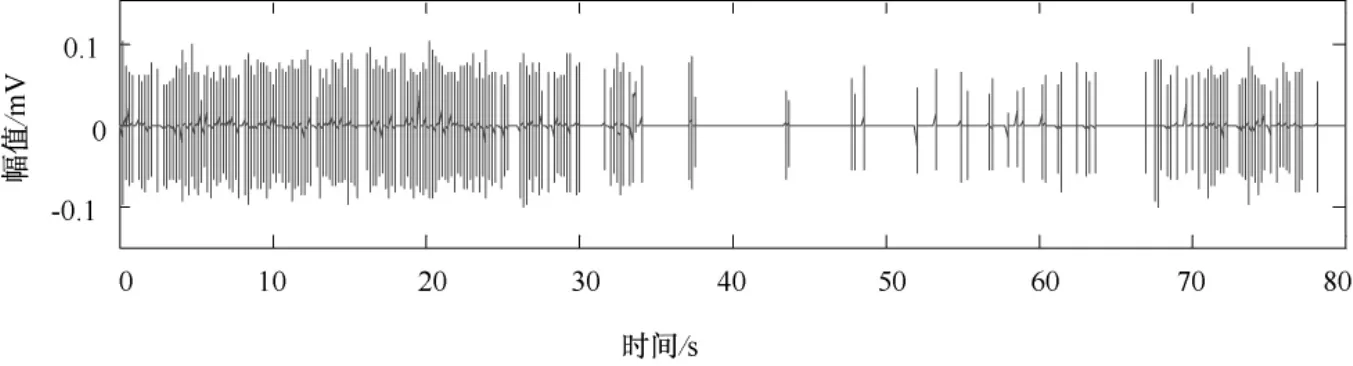
图7 大鼠初级运动皮层神经元spike序列Fig.7 Spike train of primary motor cortex in rats

从图8中可见，虽然采集到的大鼠初级运动皮层神经元spike信号的波形比较相似，但仍可以明显看出存在两类spike信号。图9为两类spike信号在相空间中计算出的关联维数分布，显示两类spike信号的关联维数具有明显的分层分布现象。图10为经K均值分类后的spike信号叠加，可看出有一部分spike信号错分，但大部分spike信号分类是正确的。这说明，基于关联维数的神经元动作电位模式分类方法应用于真实数据是有效的。

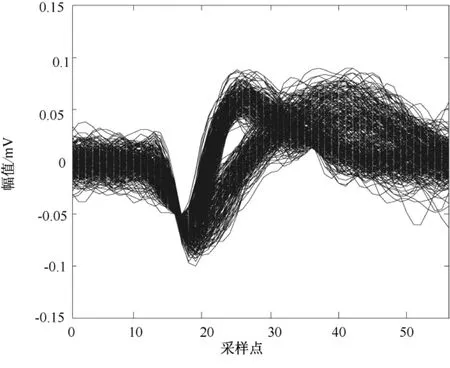
图8 大鼠初级运动皮层神经元spike信号叠加Fig.8 Spikes of rats’primary motor cortex

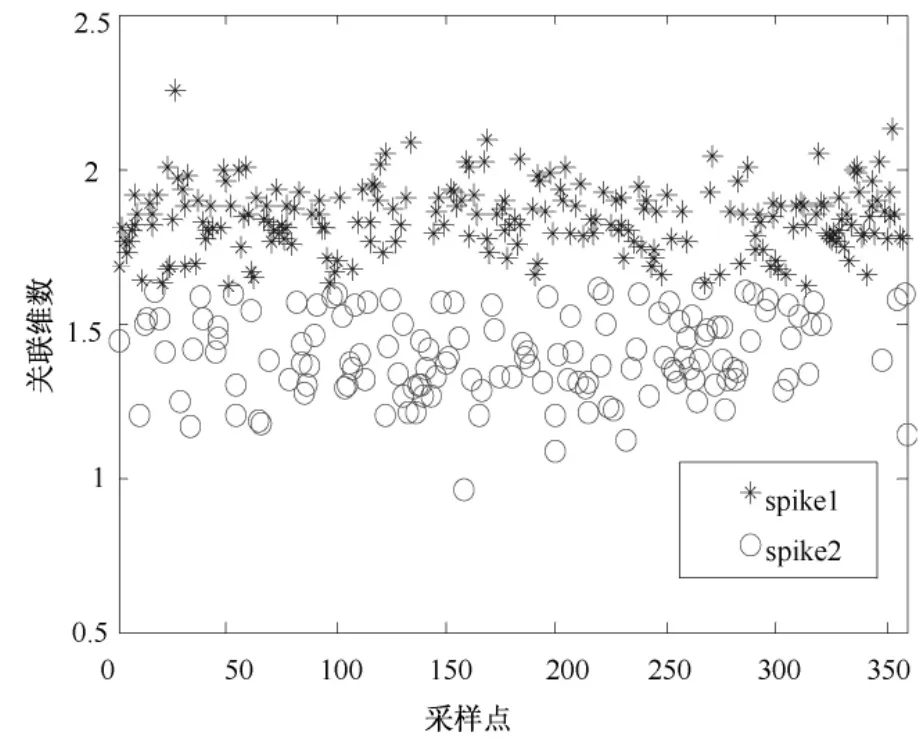
图9 spike信号关联维数分布Fig.9 The distribution of spike’s correlation dimension

由于神经元动作电位信号是时变、非平稳信号，传统的时域或频域分析都无法准确地表达神经元动作电位的特征信息。基于关联维数的特征提取优势在于它刻画了信号的非线性特性，通过将动作电位的时间序列重构到高维的相空间中，使得原本在低维空间中无法区别的特征信息在高维相空间中可以进行有效区分，增强了非同类动作电位的可区分度。真实数据的实验结果表明，本算法框架具有较好的分类效果，代替人工分类具有一定的可行性。

图10 分类后spike信号叠加Fig.10 The superposition of classified spike

6 结语

植入式多电极阵列应用中的动作电位模式分类技术，是神经编码研究的前期基础，因此有着较好的研究意义和应用前景。笔者针对神经元动作电位模式分类，提出了一种基于关联维数的特征提取及分类新算法；给出了关联维数计算过程中延迟时间和嵌入维数等关键参数的选择依据，以及算法实现的主要步骤。以仿真实验数据为例，结合K均值模式聚类方法，实现了spike信号的无监督分类。与PCA和小波变换等被广泛使用的方法进行了比较，结果证明本算法框架对仿真实验数据模式分类的准确率达到了95％以上，表明本算法具有一定的优势。在实验室环境下，进行了大鼠初级运动皮层神经元电活动的采集，并将本方法应用于真实的实验数据，取得了良好效果，证实了非同类神经元动作电位的关联维数具有较好的可分性，同时也验证了本算法的有效性。

［1］AdamosDA， Kosmidis EK， TheophilidisG. Performance evaluation of PCA-based spike sorting algorithms［J］.Comput Methods Prog Biol，2008，91（3）：232 －244.

［2］Geng Xinling，Hu Guangshu，Tian Xin.Neural spike sorting using mathematical morphology，multiwavelets transform and hierarchical clustering［J］.Neurocomputing，2010，73：707 －715.

［3］Quiroga RQ，Nadasdy Z，Ben-Shaul Y.Unsupervised spike detection and sorting with wavelets and superparamagnetic clustering［J］.Neural Comput，2004，16：1661 － 1687.

［4］Chibirovaa OK， Aksenovaa TI， Benabida A， et al.Unsupervised spike sorting of extracelluar electrophysiological recording in subthalamic nucleus of Parkinsonian patients［J］.Biosystems，2005，79：159－171.

［5］Vargas-Irwin C，Donoghue JP.Automated spike sorting using density grid contour clustering and subtractive waveform decomposition［J］.Journal of Neuroscience Methods，2007，164（1）：1－18.

［6］Delesclue M，Pouzat C.Efficient spike-sorting of multi-state neurons using inter-spike intervals information［J］.Journal of Neuroscience Methods，2006，150：16－29.

［7］彭建华，刘延柱.脑科学中若干非线性动力学问题［J］.力学进展，2003，33（3）：325－321.

［8］Kim HS，Eykholt R，Salas JD.Nonlinear dynamics，delay times and embedding windows［J］.Physica D（S0167 － 2789），1999，127：48－60.

［9］Cao Liangyue.Practical method of determining the minimum embedding dimension of a scalar time series［J］.Physica D，1997，110：43－50.