节点反投影方法在三维EIT模型中的仿真与实验研究
2011-12-31王宏斌徐桂芝张剑军颜威利
王宏斌 徐桂芝 张 帅 张剑军 李 颖 郭 磊 颜威利
(河北工业大学电磁场与电器可靠性省部共建重点实验室,天津 300130)
引言
电阻抗成像技术通过简单易行的测量手段,由边界电位信息重构出目标区域内的阻抗分布情况,即由较少的先验信息达到获得丰富内部功能信息的目的。这使得EIT技术具有低廉、简易等优势,同时在兼具无创、无放射性的基础上,可以进行其他成像手段所无法实现的功能成像。不过,其逆问题的欠定、非线性以及严重病态增添了算法研究的困难,各国研究人员提出了许多独特、巧妙的方法克服障碍,以实现阻抗成像。美国 Rensselaer Polytechnic Institute将这些方法归纳为 3种[1]:一是求解线性反问题,适用于求解场域内电阻率(电导率)变化微小的情况,典型算法如牛顿一步误差重构算法(NOSER)[2]和反投影方法[3];二是通过迭代的方法求解非线性逆问题,如牛顿迭代法[4];三是直接进行逆问题求解,如D-BAR算法[5]。本研究所描述的方法属于第一类,在传统反投影方法的投影叠加思想上舍弃了对剖分单元的计算,选择节点为计算对象实现阻抗成像。这样做减少了运算量,提高了成像速度,在三维圆柱体模型的仿真实验和水槽物理模型的实验中取得了较好的效果。
1 节点反投影方法
对EIT问题求解场域的数学描述用Laplace方程,有
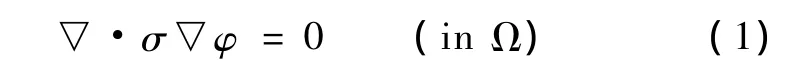
边界条件为
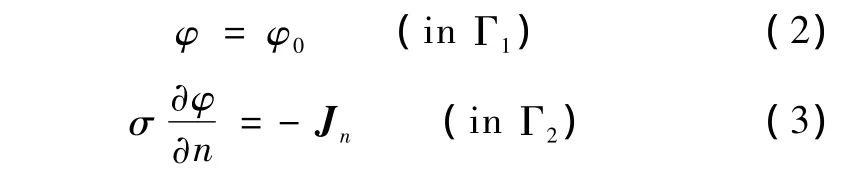
式中,σ为目标内部电导率的分布,φ0为给定边界上的电位,Jn为给定边界上外加激励的电流密度(无注入电流时为零)。
区域内的电流场任意位置的电流方向总是与等位线垂直,因此可以将EIT系统看作是一个硬场。由于电流场满足似稳条件,电场E可由标量电位函数φ来表示,即

又因为

可以得到

从式(6)可以看出,目标内电阻率 ρ(ρ=σ-1)与电位梯度成正比。当电阻率从ρ0变为ρ1时,其变化量为

即阻抗的变化与电位梯度的变化成正比。
在二维情况下,边界上各个电极测得的电位数据是一维的。由于通过等位线的电流总和是一定的,那么可以等效地假定存在一个电流源,电阻率ρ分布即为通过各等位线 l上各节点的电阻率总和,即

于是,可以将圆域的目标模型映射到一维情况中[6],如图1所示,其中x为电极所在边界位置。
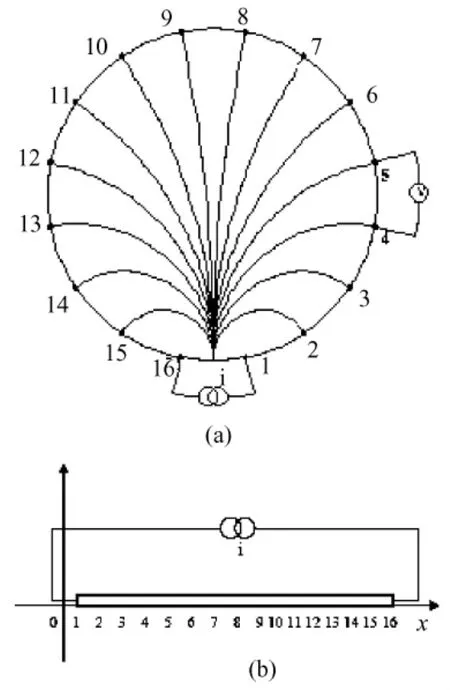
图1 EIT二维圆域模型的一维电流等效模型Fig.1 1D equivalent circuit model for 2D EIT circle model
假设等位线的等效电阻率与边界位置存在投影关系,其函数表示为
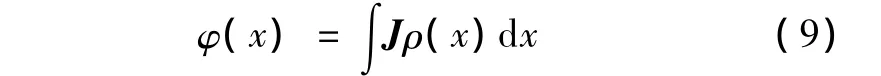
由此得到图1所示等效电路的函数,即
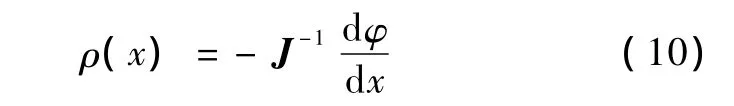
从而由式(7)得到一维映射等效模型简化形式为
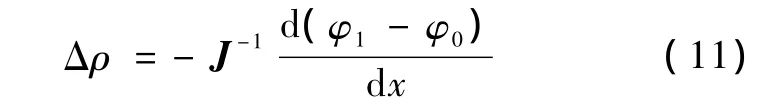
这样,就可以通过边界电位的变化情况,得到区域内部电阻率的变化情况。将这一变化沿电阻率均匀分布时确定的投影路径,反投影至所对应的区域内部等位线上的各节点,通过多次激励测量和叠加运算,得到区域内部的阻抗变化情况,从而实现了动态阻抗成像。因此,该方法得名为节点反投影方法(node back projection algorithm,NBPA)[7]。
在三维情况下,圆柱体边界展开后为一个二维平面,由式(7)展开后其二维映射等效形式为电位变化量对二维坐标的导数(即梯度形式),故仍由式(7)形式表示为宜。
由于节点反投影方法需通过相邻激励模式在场域内形成投影域,因而其边界电压分布为一单调曲线。针对节点反投影方法对边界坐标的函数关系的单调特点,多项式曲线拟合方法[8]通过有限的测量数据,拟合出边界电位曲线。
在三维圆柱体模型中,采用4层同时激励的相邻激励模式,即每次激励4层中编号相同的电极对,依次进行1-2,2-3,…,16-1的4层同时激励。这样,使圆柱体边界上电压分布在应用最小二乘法拟合时情况较为特殊。将圆柱体侧面展开为二维xoy平面,取电极处电压为z轴上的坐标值,建立直角坐标系。4层电极上电压数据构成的平面近乎平行于xoy平面。由最小二乘法计算拟合曲面,多项式包含z项时无法通过改变阶数将边界电压数据拟合为一适合平面。因此,考虑了4层同时激励模式的特殊性,在拟合多项式中舍去了 z项,得到拟合曲面,如图2所示。

图2 边界电位拟合曲面
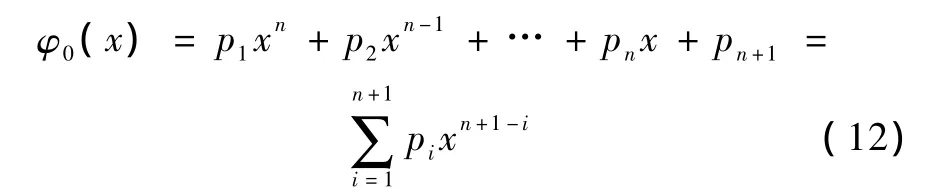
式中,n为拟合多项式的预设阶数,x为边界位置坐标,pi(i=1,2,…,n+1)为各项系数。
由式(12),可以计算出内部各节点电位对应边界电位在拟合曲线上的坐标。当区域内部阻抗发生变化时,边界电位亦发生变化。节点反投影方法即由此来实现逆问题求解。
在区域内阻抗发生变化的t1时刻测得边界电位,经曲线拟合后得到多项式为

式中,n为拟合多项式预设阶数,x为边界位置坐标,pi(i=1,2,…,n+1)为各项系数。
将式(12)和式(13)代入式(11),可得
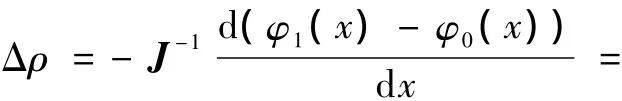
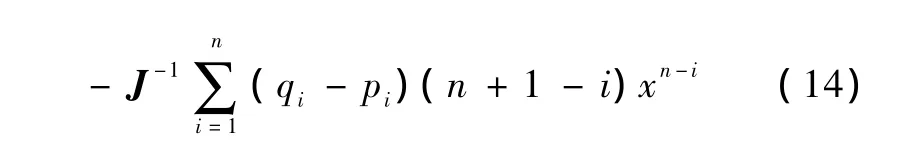
由此,可以得到区域内部各个节点处的电阻率变化情况,从而实现图像重构。
由文献[9]中对先验信息的定义,在由正问题计算投影位置时,利用边界电压在4层同时相邻激励时的单调性,对处于已知电压的电极之间的边界点进行了拟合近似,因此可以说通过边界电压拟合,丰富了先验信息。
2 算法验证实验
2.1 仿真实验
建立了半径10 cm、高10 cm的圆柱体仿真实验模型,分别在距底面2、4、6、8 cm的截面处每层都放置16个电极,从而形成16×4的电极阵列,如图3所示。
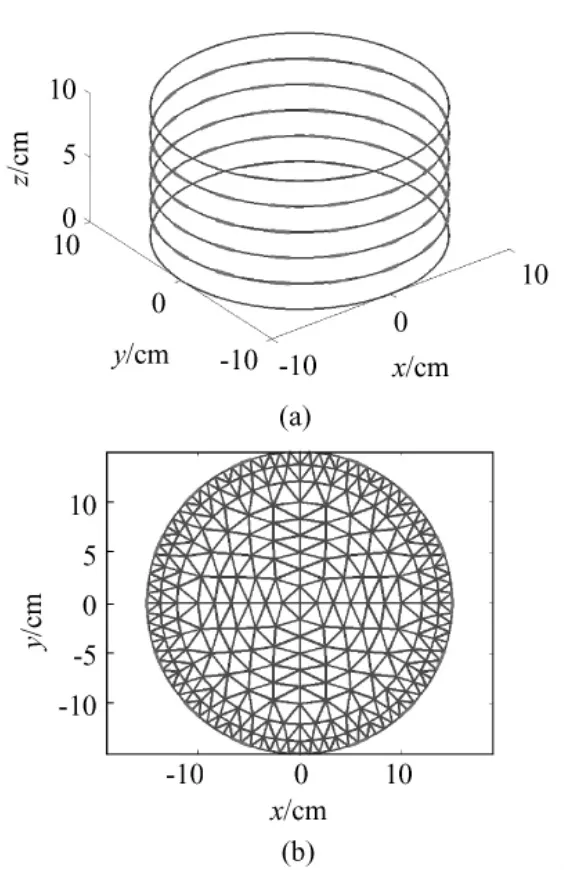
图3 三维圆柱体仿真模型。(a)侧视图;(b)截面图Fig.3 3D cylindrical simulation model.(a)lateral view;(b)section
应用有限元方法(finite element method,FEM)进行三棱柱剖分,自下而上均匀分为10层,每个截面剖分为9层。在圆柱体模型中,剖分单元5 040个,节点3 311个。
在对圆柱体模型进行仿真时,将测得的16组、4层电极上的电压数据,用节点反投影方法进行处理,得到4层截面内部阻抗信息的重建图像。
在仿真实验中,对式(14)进行处理后应用于编程可简化计算。由于外部激励的电流是恒定的,即一维等效电路中的电流是恒定的,因此可以假定从而使得式(11)简化为

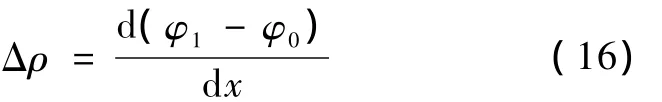
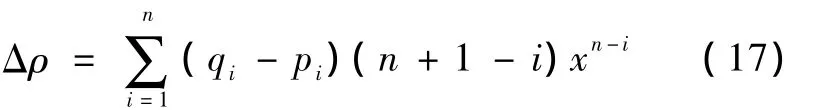
通过式(15)的假定得到式(17),在一定程度上简化了编程。
在模型中放置目标Ⅰ,设定其电阻率为3 Ω·m,圆柱体区域内其他部分的介质电阻率为2 Ω·m,如图4所示。
进行曲线拟合的推导,可得
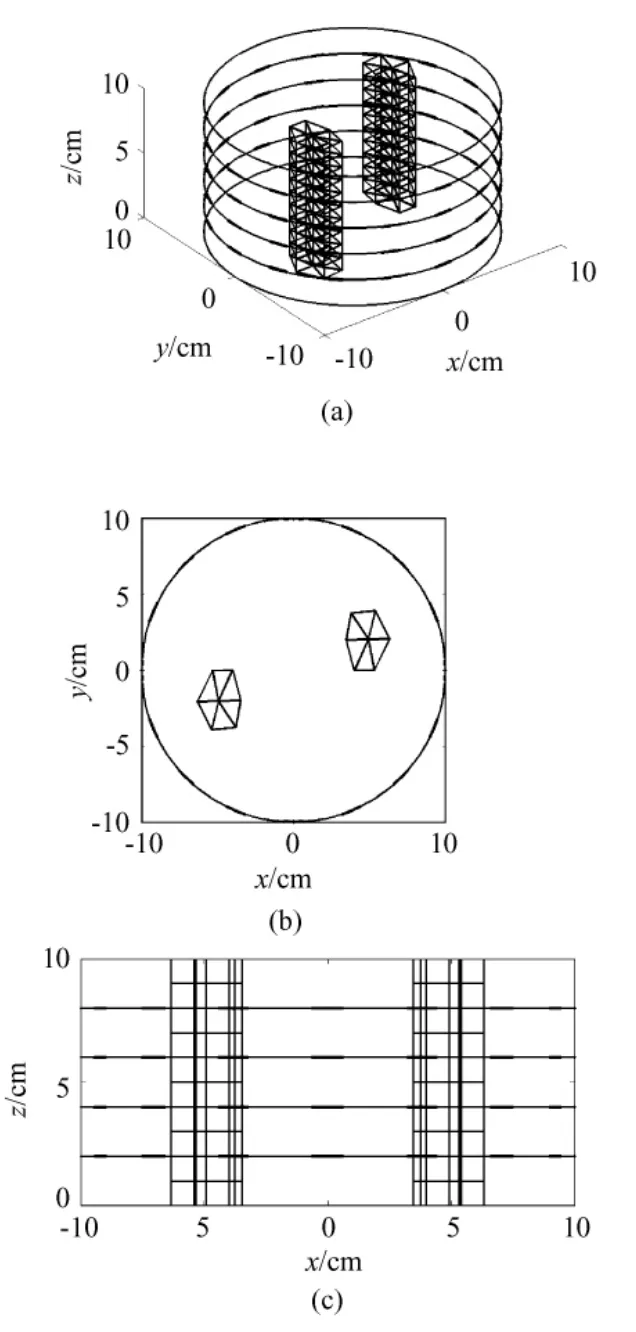
图4 目标Ⅰ的仿真模型。(a)侧视图;(b)俯视图;(c)平视图Fig.4 Simulation model of target.(a)lateral view;(b)top view;(c)front view
为了考察节点反投影方法对三维空间的适应性,在圆柱体模型中放置目标Ⅱ,如图5所示。设定目标Ⅱ的两物体电阻率为3 Ω·m,圆柱体区域内其他部分的介质电阻率为2 Ω·m。目标Ⅱ与目标Ⅰ的不同之处在于其两物体的水平高度不同,在竖直方向上形成了一部分交错。左侧目标柱体底部距离圆柱体模型底部1 cm,高4 cm,即其跨越自下而上的第一、二层电极所在平面;右侧目标柱体底部距离自下而上第二层电极所在平面1 cm,高4 cm,即其跨越自下而上第三、四层电极所在平面。如此,除自下而上第二层和第三层电极平面之间外,各层电极所在平面上仅存在单一的目标物体。
为了对算法重建结果进行更好的说明,引入总体误差[10],即
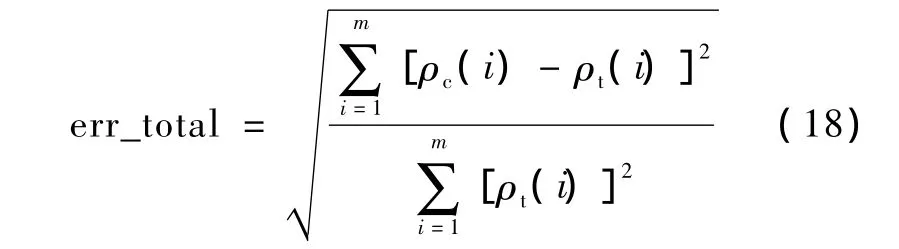
式中,ρc(i)为计算获得重建电阻率分布,ρt(i)为设定电阻率分布,m为电阻率分布矢量维数。
2.2 物理模型实验
实验室设计了128通道(4层电极,每层16个复合电极)的 EIT实验系统[11],利用节点反投影方法进行物理模型实验。实验水槽直径30 cm,高30 cm,如图6所示。在其边界上的16×4电极阵列中,采用的是4 cm×2 cm的矩形铜片电极,其激励与测量部分之间由绝缘子隔离。在竖直方向上,相邻两个电极相距2 cm。水槽底部距离第1层电极下沿所在平面4 cm,水槽顶部距离第4层电极上沿所在平面4 cm。

图6 实验模型Fig.6 Experimental phantom with target
在实验模型中盛满 NaCl溶液(电导率约为0.08S/m),然后将不同电导率的材料(环氧树脂棒等)放入模型中进行实验。采用4层同步激励模式且同时测量,各层均采用相邻激励-相邻测量模式。每次激励施加于各层之上的电流幅值小于0.5 mA,频率为100 kHz。由于信号频率较低,故虚部影响可以忽略,仅考虑阻抗实部进行计算。
在实际操作中,以未放入任何目标时模型内NaCl溶液的电导率分布作为参考数据。在放入具有不同电导率的材料之后,系统进行数据采集,将这些数据与参考数据输入计算机,由所编写的节点反投影成像程序进行断层图像重建。
将长度为18 cm、直径为2.5 cm的透明树脂棒垂直浸入模型,直达底部,树脂棒上部距离第4层(与仿真模型一致,电极依旧自下而上分布在1~4层)电极所在平面6 cm,
3 结果
3.1 仿真实验结果
由式(17)对图4所示目标Ⅰ进行节点反投影图像重建,自下而上的各截面结果如图7所示。
在圆柱体模型中,目标Ⅰ两物体均为与模型等高的柱体,且其位置中心对称。图7(a)是节点反投影方法的成像结果,相对于图7(b)传统反投影方法的重建图像,不仅很好地显示出了目标Ⅰ两物体的形状和位置,而且伪影也较少。图7(b)中目标物体附近的伪影扩散较为严重,边界较模糊,而图7(a)中目标物体附近没有扩散现象,边界圆润,与设定中的目标物体更为相似。同时,模型内距目标物体较远的区域中图像几乎没有杂乱的伪影,这与图7(b)中的伪影分布有很大不同,说明成像效果有所提高。实验结果表明,节点反投影方法可以通过电极激励截面测得的电位信息,对区域内部的多个三维体进行重建,而且效果较传统反投影方法有所提高。

图7 目标Ⅰ的仿真重建图像(每列自下而上依次为第1~4层)。(a)节点反投影方法的成像结果;(b)反投影方法成像结果Fig.7 Reconstruction of target Ⅰ(bottom-up section 1~4).(a)reconstruction images by NBPA;(b)reconstruction images by BPA
用节点反投影方法对图5所示目标Ⅱ进行图像重建,各截面结果如图8自下而上所示。
在图8中,两种方法均清晰地显示出了目标Ⅱ中的两物体,但竖直方向上的差异体现得略有不同。图8(b)的传统反投影方法重建图像依旧存在目标物体附近伪影扩散、形状与设定差距稍大的问题,同时在分辨竖直方向上目标物体的差异时敏感性稍逊。在图8(a)中,第2层上右侧目标物体和第3层上左侧目标物体的图像更为清晰。节点反投影方法可以更好地重建目标Ⅱ中两个物体的空间结构,说明其具有较好的三维空间识别能力。
在图8中,两种方法重建图像均存在对第1、2层右侧目标物体和对第3、4层左侧目标物体的显示痕迹,这是因为在模型内部放入电阻率不同的目标物体后,改变了电流场的分布情况。由于电流场的软场特性,发生变化的范围会影响到其他层上,从而在跨层截面上出现对目标的反应,是正常现象。式(7)正是这种现象的数学表达。而节点反投影方法分辨目标物体的敏感性,使其在重建图像中此部分伪影稍浓。如将两种方法相结合,则可取长补短地解决分辨敏感性与伪影的矛盾。
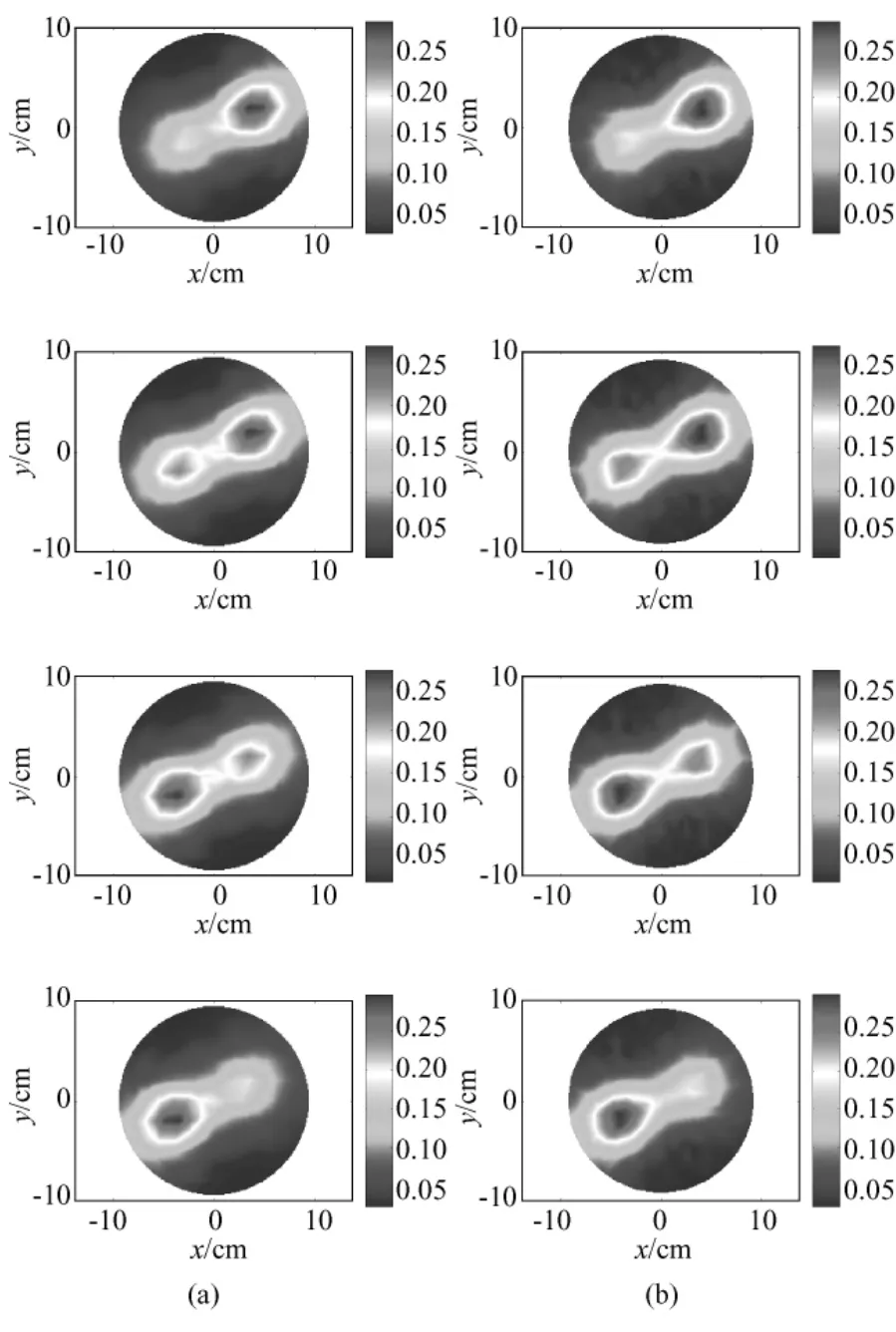
图8 目标Ⅱ的仿真重建图像(每列自下而上依次为第1~4层)。(a)节点反投影方法的成像结果;(b)反投影方法的成像结果Fig.8 Reconstruction of target Ⅰ(bottom-up section 1~4).(a)reconstruction images by NBPA;(b)reconstruction images by BPA
用式(18)所述的总体误差对两种方法的重建图像进行比较,结果如表1所示。

表1 节点反投影方法与传统反投影方法总体误差比较Tab.1 Comparison of NBPA and BPA in total error
从表1中可以看出,节点反投影方法的重建结果比传统反投影方法重建结果分别降低总体误差8.87%和6.85%。
3.2 物理模型实验结果
用节点反投影方法对图6所示的实验模型进行重建,结果如图9所示。

图9 实验模型重建图像。(a)第1层;(b)第2层;(c)第3层;(d)第4层Fig.9 Reconstruction images of experimental model.(a)section 1;(b)section 2;(c)section 3;(d)section 4
图9中的重建结果很好地将水槽内的目标物体棒显示出来,说明节点反投影方法具有良好的空间分辨能力。
4 讨论与结论
节点反投影方法选择了节点作为计算对象,这与大多数方法针对剖分单元进行计算的方式不同。一般情况下,有限元方法剖分所得到的节点数远小于单元数。选择节点为计算对象,降低了计算中矩阵的阶数,减少了运算量,大大降低了对计算机硬件和数学软件的要求,在节省运算时间的基础上相对提高了计算精度。
在EIT问题中,内部阻抗的变化会引起边界电位的变化。相对区域内丰富的阻抗信息,有限的电极数所测得的电位明显单薄。边界电位的拟合,增加了可用的信息。通过推导,得到边界电位与内部节点电位的关系,使得边界电位拟合不单起到增加先验信息的作用。将离散的电极(文中采用的模型为每周16个)信息扩展为一条曲线,为数学计算架起了桥梁。
仿真实验显示,节点反投影方法在三维模型中具有一定的适应性。模型中所放置的多个物体的重建图像,基本反映了其形状和位置。与传统反投影方法相比可以看出,节点反投影方法具有更好的成像效果、更为准确的目标物体形状重建能力。水槽模型实验印证了节点反投影方法在三维物理模型中的适应能力,重建图像中目标物体处的边界柔和、伪影不多,为将来进行去除伪影的工作提供了良好的条件。重建图像尤其体现了节点反投影方法具有一定的三维空间识别能力,较为准确地重构了目标物体在竖直方向的形状和位置。其存在的误差分析推测为:目标物体的存在,使电流走向发生了偏转。针对由此造成的空间分辨问题也是下一步的研究重点之一,与伪影消除有着紧密的联系。
本算法是一种动态反投影算法,需要首先采集背景边界电压的分布情况,方可进行差分成像。因此,与其他动态算法一样,适合于对人体肺部成像。对于人体内部电阻率不发生周期性变化的部位,如头部、手臂等,该方法则无法通过多次测量求平均来得到与实时变化有差异的背景电压,因而不能进行差分成像。此外,节点反投影方法在推导中的一些假设可以更加贴近实际情况,有些地方可以通过更加完善的数学理论来加以雕琢。研究表明,不同层间电极信息与节点的关系为下一步的研究重点。综上所述,节点反投影方法具有深入挖掘的潜力。
[1]Siltanen S.Electricalimpedance tomography and Faddeev Green’s functions[D].Helsinki:Helsinki University of Technology,1999.
[2]罗辞勇.基于快速牛顿一步误差重构的电阻抗成像算法和实验研究[D].重庆:重庆大学,2005.
[3]徐管鑫.电阻抗成像技术理论及应用研究[D].重庆:重庆大学,2004.
[4]Cheney M,IsaacsonD,NewellJC.Electricalimpedance tomography[J].SIAM Review,Society for Industrial and Applied Mathematics,1999,41(1):85-101.
[5]Siltanen S,Jennifer M,Isaacson D.An implementation of the reconstruction algorithm of A Nachman for the 2D inverse conductivity problem[J].Inverse Problems,2000,16(3):681-699
[6]张剑军.节点反投影法电阻抗成像研究[D].天津:河北工业大学,2008.
[7]Zhang Jianjun,Yan Weili,Xu Guizhi,et al.A new algorithm to reconstructEIT images:node-back-projection algorithm[C]//Proceedings-29th Annual International Conference of the IEEE-EMBS.Piscataway:IEEE,2007:4390-4393.
[8]Zhang Jianjun, Xu Guizhi, Zhao Quanming, et al. Using polynomial curve fitting method to improve image quality in EIT[C]//Proceedings-28th Annual International Conference of the IEEE-EMBS.Piscataway:IEEE,2006:6769-6772.
[9]程民德,何思谦,张景中,等.数学辞海(第五卷)[M].北京:中国科学技术出版社,2002:86.
[10]吴焕丽.三维电阻抗成像问题研究[D].天津:河北工业大学,2009.
[11]Xu Guizh,Wang Renping,Zhang Shuai,et al.A 128-electrode three dimensionalelectrical impedance tomography system[C]//Proceedings-29th Annual International Conference of the IEEE-EMBS.Piscataway:IEEE,2007:4386-4389.
