经硬脑膜电刺激对视皮层神经活动影响的仿真研究
2011-12-31侯文生郑小林吴小鹰阴正勤JIANGYingtao
夏 楠 侯文生* 章 毅 郑小林 吴小鹰 阴正勤 JIANG Yingtao
1(重庆大学生物工程学院,重庆 400044)2(第三军医大学西南医院眼科,重庆 400038)3(Department of Electrical and Computer Engineering,University of Nevada,Las Vegas,NV 89154,USA)
引言
经硬脑膜对视皮层电刺激为视觉功能修复提供了一种新的技术思路[1],即通过置于颅骨下、硬脑膜上的微电极阵列对视皮层进行刺激,相对植入视皮层内部的视觉假体[2]而言,它具有手术难度低、对视皮层组织损伤小等优点。但经硬脑膜的刺激电流需要流经硬脑膜、脑脊液等组织才能到达目标视皮层组织,认识和掌握刺激电流对目标皮层的作用效果非常必要。目前许多学者采用有限元法、边界元法或有限体元法等数值方法来求解组织内的电场分布[3],尝试用激活函数判定电场对神经元电活动影响的可行性[4];本课题组在之前工作中也通过建立猫视皮层的有限元模型,利用激活函数来表征电极的作用范围,即主观选取某个阈值来定义组织活化区,定性的讨论经硬脑膜对目标皮层施加电刺激时电极的作用效果,初步证实了经硬脑膜刺激的可行性[5]。
NEURON是一款由耶鲁大学Carnevale和Hines开发的神经计算软件,为单个神经元和神经网络的理论仿真提供一个方便快捷的研究平台,CameronC.McIntyre和 WarrenM.Grill等人借助此平台研究了深部脑刺激中高频电刺激对电极周围神经元是否有兴奋或抑制效应,并很好地确定了该效应的范围[6]。由于激活函数判定方法的阈值选取是主观的,可能会影响仿真工作的准确性,所以本课题组在之前工作的基础上,采用了一种新的方法,即将神经元模型耦合到有限元模型中,进一步确定经硬脑膜刺激时,电极对视皮层的作用范围。首先采用基于有限元法来分析不同刺激模式下脑组织内的电场分布,然后将电位加载到在NEURON软件中构建的神经元计算模型上,通过NEURON软件计算不同位置神经元是否发生动作电位来判定电极的作用范围及不同刺激模式的作用效果。
1 方法
1.1 脑组织内电场分布分析
选用COMSOLMultiphysics 3.5a(COMSOL Inc.,Burlington MA,USA)建立有限元仿真模型[5,7],模型结构见图 1 中(a)和(c)。模型中采用3×3电极阵列进行仿真研究,其结构如图1(b)所示。它是一种表面电极阵列,每个电极为等直径的圆柱体,内部设有通孔。基底近似于矩形,大小与初级视皮层区域外表面积相当,具体参数见表1。金属导线位于基底内,向外延伸至焊点处(未画出)。由于是对单侧大脑半球进行刺激,故模型一侧边界取为大脑镰与非刺激侧大脑半球的交界面。模型总体尺寸为15 mm×10 mm×15.2 mm,具体尺寸参数信息见文献[5,7]。
由于施加的是低频刺激(小于10 kHz),此时可忽略生物组织的介电常数和电导率在不同空间位置的差异,将其视为各向同性均匀分布[5],模型各部分电学参数见表2。对模型进行边界条件设定以及网格的划分后对模型进行求解,以得到经硬脑膜刺激后的皮层内电场分布。

图1 经硬脑膜对猫视皮层电刺激仿真模型。(a)三维仿真模型;(b)刺激电极阵列;(c)经刺激电极轴线的二维截面Fig.1 Simulation modelofepiduralelectrical stimulation applied on the cat's visual cortex.(a)3D view of the model;(b)stimulating electrodes array;(c)2D cross section through the axis of one electrode
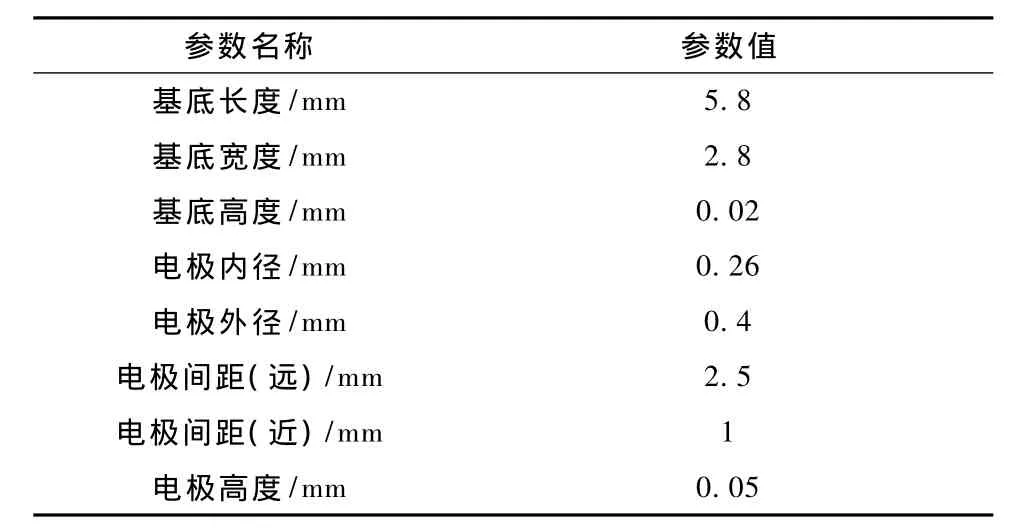
表1 刺激电极阵列模型参数Tab.1 Dimensions of electrodes array model
1.2 神经计算软件原理
NEURON软件基本原理是通过求解线缆方程[8],即式(1)得到神经元在不同时刻的膜电压。Iinj表示刺激电极流入胞内的电流,cm和 rm分别表示膜电容和膜电阻,Vrest代表细胞的静息电位,Vm为神经元的跨膜电位。其基本方法就是根据神经元生理结构的差异将其分成若干节段,每个节段的生理结构电学性质完全相同,可等效为直径不变的圆柱体,形成概念模型[7-8],随后根据计每个节段计算精度要求将其分成若干隔室,每个隔室用等效电路代替,形成计算模型[7-8],并进行计算,如图 2所示。获得理论结果后,与实际生理模型进行比较,并对理论模型不断进行改进,从而得到更精确的计算结果。其中隔室分的越多则计算精度就越高,但相应的计算量越大。

表2 模型电学参数Tab.2 Electric parameters in simulation model
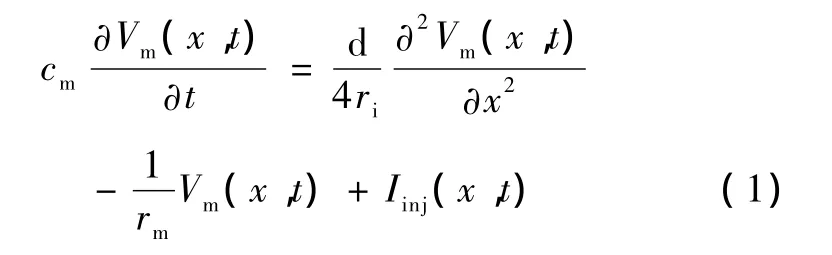
图2 NEURON 计算过程[13]Fig.2 Computating process of NEURON
1.3 神经计算方法
首先在NEURON中建立神经元模型。为了使仿真结果为动物实验提供理论指导,本研究以猫初级视皮层第III层内的锥体细胞为研究对象,该模型由 Mainen根据 Mainen和 Sejnowski的报道[9]所建立,在此基础上,增加了轴突结构如图3(b)所示,除树突、轴突、胞体外,还包括轴丘、起始段等完整的神经元解剖结构。其次,在有限元模型(图1)体坐标中建立一个11×11的二维正方形点阵,相邻两点间距0.2 mm。该点阵位于中心电极正下方,平行于电极基底,猫初级视皮层第III层内的锥体细胞对应位置,且矩阵中心点对应中心电极正下方神经元,矩阵边缘包含了两个近端电极下方皮层的神经元活动信息,如图3(c)所示。
点阵中每一点代表一个神经元,若某一点位置上的神经元爆发动作电位,就可认为以该神经元为中心的0.01 mm2区域内的神经元均发生兴奋。由于建立的脑模型尺寸远小于猫脑直径(约5 cm),为简化问题,可认为在该区域中的神经元都为此种神经元。最后通过NEURON中的play函数将傅里叶-有限元方法计算出的电位加载到相应位置的神经元模型上,并计算该神经元是否发生兴奋,从而得到电极的作用范围。
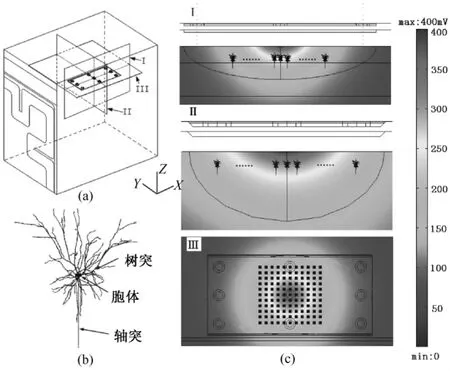
图3 神经元模型与皮层关系示意图。(a)有限元模型中的特征截面;(b)猫视皮层第III内锥体细胞神经元模型;(c)神经元点阵分别在截面Ⅰ、Ⅱ、Ⅲ中的位置Fig.3 Relationship between neuron model and cortex.(a)characteristic crosssectionsin Fourier finite element model;(b)model of the pyramidal cell in layer III in cat's visual cortex;(c)the position of neuron dot array in cross sectionⅠ,Ⅱ,Ⅲ
1.4 刺激参数的选择
实验选取双向脉冲、指数脉冲和正弦波3种刺激形式,来研究经硬脑膜电刺激时,刺激形式的改变对视皮层内神经元作用范围的影响。3种刺激形式的波形和主要参数见表3。3种刺激波形由Matlab自带数学函数产生,通过设置波形的脉宽、幅值和频率来改变刺激模式。
2 结果
2.1 不同波形刺激时,皮层内神经元的响应范围
实验选取3种波形的基准刺激幅值为0.8mA,刺激频率为200Hz,其中双向方波脉冲的正向基准脉宽为0.2 ms。皮层内电场分布及神经元点阵中的响应区域结果见图4。
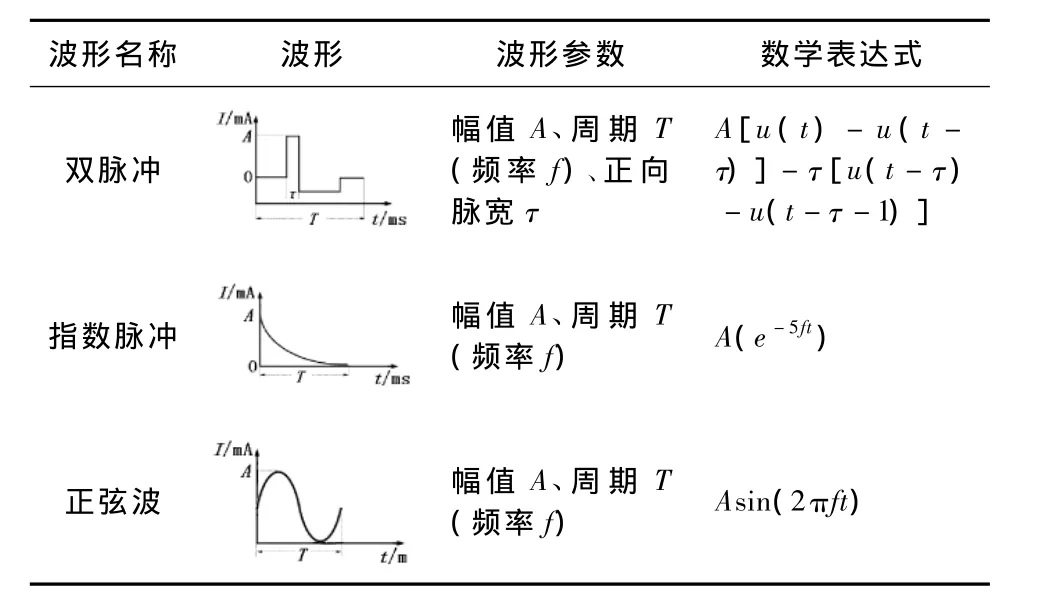
表3 3种刺激波形参数Tab.3 Parameters of three stimulus waveforms

图4 3种波形刺激结果(黑色点表示未响应的神经元区域,白色点表示爆发动作电位的神经元区域,箭头指向大脑镰方向)。(a)截面Ⅲ中的神经元点阵;(b)双脉冲刺激;(c)指数脉冲刺激;(d)正弦波刺激。Fig.4 The results of three stimulus waveforms(black dot represents the unexciting neuron,the white dot represents the excitatory neuron,the arrow indicates the cerebral falx direction.).(a)neuron dot array in cross section Ⅲ;(b)bipulse stimulus;(c)exponential pulse stimulus;(d)sinusoidal pulse stimulus.
从图4可看出,3种波形都引起发了神经细胞的兴奋,不同的刺激波形引发的神经元区域兴奋数量不等。在所有的刺激方式下,靠近大脑镰一侧的神经元区域兴奋的数量都多于远离大脑镰方向的神经元区域数量,且响应平面区域呈一个以刺激电极点为中心的非对称不规则圆形。
神经元的兴奋与其膜外电位有关,本研究在有限元模型中第Ⅰ平面上神经元放置区域做了一条特征截线L,如图5(a)所示,箭头指向大脑镰方向,截线L的电位曲线如图5(b)所示。图5(b)中电极中心位置为零,可以看出在对称位置上电压不等,近大脑镰一侧电压略高于远离大脑镰一侧的电压,在下面的结果中都存在这种现象。
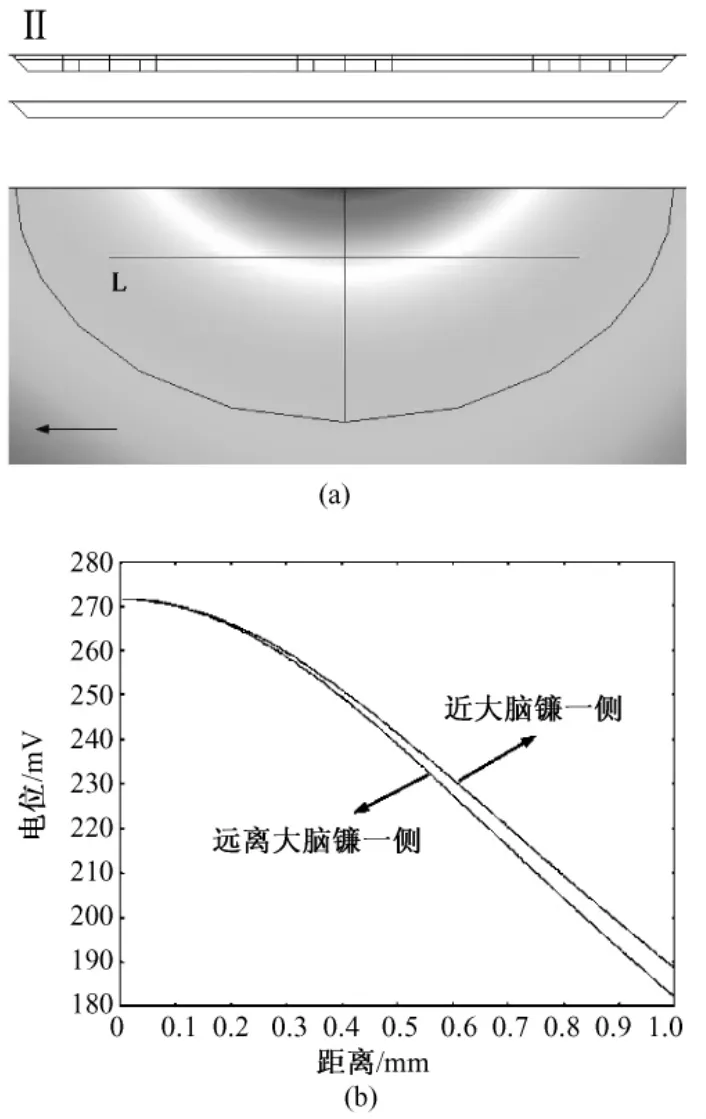
图5 特征截线L的电位分布。(a)特征曲线L的位置;(b)曲线L上的电位Fig.5 Potential distribution in characteristic line L.(a)position of line L;(b)electric potential on line L.
2.2 刺激幅值的变化对皮层内神经元响应范围的影响
刺激幅值变化也会引起皮层内电场分布改变,因此也会引起皮层内的神经元区域兴奋数量变化,图6(a)显示了在不同幅值作用下神经元兴奋数量的变化情况。三种波形的刺激频率为200Hz,其中双向方波脉冲的正向脉宽为0.2 ms。
从刺激结果来看神经元响应的区域都随着刺激幅值的增加而增大,用指数波进行刺激时,幅值减小到0.5 mA皮层依然有9个神经元区域爆发动作电位,随着刺激幅值的增大,矩阵内神经元区域响应个数快速增多,幅值增加到0.8 mA时近大脑镰一侧神经元响应区域到达点阵的边缘(如图4(c)),0.9 mA时响应区域已经超出了点阵。双向脉冲刺激时,随着刺激幅值的增大矩阵内神经元区域响应个数随之增加,但只有刺激幅值高于0.7 mA时神经元才有响应。正弦波在同等幅值作用下响应的神经元范围要远远大于前两种刺激,幅值增大到0.9 mA时矩阵内神经元区域全部发生兴奋。
2.3 脉宽以及频率改变对皮层内神经元的影响
脉宽也是方波脉冲的重要调节参数,分别用幅值为0.8 mA、正向脉宽为0.2、0.3和0.4 ms的双向脉冲对模型进行刺激,刺激频率为200Hz,所得到的神经元区域响应结果见6(b)。用幅值为0.8 mA、频率分别为100、200和300Hz的指数脉冲、正弦波和双脉冲刺激目标皮层,其中双向方波脉冲脉宽为0.2 ms,结果见图6(c)。
图6 改变刺激参数对神经元区域兴奋数量的影响。(a)改变刺激幅值;(b)双脉冲刺激下脉宽变化;(c)改变刺激频率Fig.6 Varies of the number of excitatory neuron regions with different stimulus.(a)different stimulation amplitude;(b)different duration under bipulse stimulus;(b)different frequency of three stimulus waveforms
从图6(b)可以看出在刺激幅值和频率不变时,增加正向方波的脉宽皮层内响应的神经元区域也随着增大,但是增加或减小双向方波脉冲的频率对刺激范围没有影响,如图6(c)所示,说明用双向方波脉冲刺激时,在正向方波占空比较小的情况下,视皮层内神经元对刺激频率变化不敏感,而对脉宽的变化非常敏感,脉宽由0.2 ms增加到0.3 ms时,响应的神经元区域个数从7个增加到47个,由0.3 ms增加到0.4 ms时响应区域个数增加到76。在幅值不变条件下,随着刺激频率的增加指数脉冲和正弦波引发的神经元区域响应个数都有减小的趋势,当频率增大时,刺激周期减小,正向刺激电荷量相应减少,从而引起皮层内神经元区域响应数量减少。因此在考虑非方波刺激形式对视皮层内神经元响应区域数量影响时,频率也是比较重要的因素。
3 讨论与总结
由于锥体细胞占到皮层内细胞总量的80%,且为易兴奋细胞[10],因此本研究只选用猫脑初级视皮层内第III层内的锥体细胞作为分析对象,将其排列成间距为0.2 mm的二维点阵耦合到有限元模型中,间距设置越小,点阵中的神经元个数就越多,所描述的响应范围越精确,但计算量也随之增大,综合考虑间距定为0.02 mm较合适。与之前的仿真方法[5]相比,本研究将选定的神经元耦合到傅里叶-有限元模型中(图3),将计算出的电位直接加载到各神经元上即可得到电极的作用范围,减少了主观选取阈值的不确定性,可以清楚、直观地描述出神经元响应区域的细微差别(如图4),因此该方法有一定的优越性。
研究选取双脉冲、指数脉冲和正弦波3种刺激波形,从实验结果看,3种波形都可引起皮层内神经元的兴奋,且兴奋区域都呈一个非对称的近圆形(图4),近大脑镰一侧的神经元区域兴奋的数量多于远大脑镰侧的兴奋数量。近大脑镰一侧皮层被脑脊液包围(图1),而脑脊液电导率远大于其他组织电导率[7],且其电导率的细微变化都会较大程度地影响模型电位分布[7],所以该解剖结构的差异使得近大脑镰侧的神经元膜外电位略高于远大脑镰侧电位(图5),从而引起了兴奋区域的不对称性。
在减小3种波形刺激幅值时,神经元区域兴奋数量也随之减少,这与文献[5]的结论相符。但本研究仿真中也得出了与文献[5]不一致的结果:一方面,在一定范围内增大或减小双向方波的刺激频率并没有使刺激范围发生变化(如图6(c)所示),对于双向脉冲而言,在单个周期内正向脉冲刺激完成后,组织内剩余电荷立刻被反向电流抵消,从而消除了每个周期组织内电荷的累积[12],而改变刺激的重复频率只改变了刺激的时间间隔,并没有改变输入的电流量,因此不能引起更多神经元的兴奋;另外,在一定范围内减小指数脉冲重复频率时,电极的刺激范围有增大趋势,对指数波而言,减小重复频率相当于增加了单个周期内流入皮层内的电流量[11],从而使响应范围增大。
本研究只关注电极在不同刺激模式下所产生的电场对皮层内神经元的作用范围,因此是将单个神经元视为独立个体,形成一个平面点阵来讨论的,并没有构建神经元网络来讨论神经元之间的影响,且只针对视皮层内某一平面的神经元活动做了定量分析,仅讨论了平行于电极的某个二维平面的神经元响应范围,没有考虑刺激深度的问题,因此对于两种软件的结合使用还需要更深一步的优化,从而得到更准确的结果。
[1]郭冰冰,侯文生,阴正勤,等.一种经硬脑膜的多通道视觉诱发电位实验测试系统的设计[J].仪器仪表学报,2009,30(6,增刊):204-207.
[2]牛金海,刘易非,任秋实,等.视觉假体:带给盲人光明的电子设备[J].中国科学(E辑:信息科学),2007,37(10):1354-1362.
[3]颜威利,徐桂芝,著.生物医学电磁场数值分析[M].北京:机械工业出版社,2006.
[4]Wongsarnpigoon A,GrillWM.Computationalmodelingof epidural cortical stimulation[J].J Neural Eng,2008,5:446 -454.
[5]侯文生,章毅,郑小林,等.基于有限元法的硬脑膜外视皮层电刺激仿真研究[J].中国生物医学工程学报,2010,29(4):557-563.
[6]McIntyre CC,Grill WM,Sherman DL,et al.Cellular effects of deep brain stimulation:model-based analysis of activation and inhibition[J].J Neurophysiol,2004,91:1457 - 1469.
[7]张毅.经硬脑膜对视皮层电刺激的数字仿真[D].重庆:重庆大学,2010.
[8]Dominique D.The somatic shunt cable model for neurons[J].Biophysical Journal 1984,46:645-653.
[9]Mainen ZF,Sejnowski TJ.Influence of dendritic structure on firing pattern in model neocortical neurons[J].Nature,1996,382:363-366.
[10]寿天德.视觉信息处理的脑机制[M].上海:上海科技教育出版社,1999.
[11]Sahin M,Tie Yanmei.Non-rectangular waveforms for neural stimulation with practical electrodes[J].J Neural Eng,2007,4:227-223.
[12]Lilly JC,Hughes JR.Brief,noninjurious electric waveform for stimulation of the brain[J].Science,1955,121:468 -469.
[13]Carnevale NT,Hines ML.The NEURON Book[M].New York:Cambridge University Press,2006.
