利用元胞自动机法模拟电渣重熔钢锭定向凝固组织

陈明秋，李宝宽，赵 林

(1.东北大学 材料与冶金学院，沈阳 110004;2.中国第一重型机械集团公司，黑龙江，富拉尔基 161042)

利用元胞自动机法模拟电渣重熔钢锭定向凝固组织

陈明秋1，李宝宽1，赵 林2

(1.东北大学 材料与冶金学院，沈阳 110004;2.中国第一重型机械集团公司，黑龙江，富拉尔基 161042)

本文应用元胞自动机法发展电渣重熔钢锭组织结构的计算模型，建立基于高斯分布的连续形核模型和生长模型;在节点上采用元胞自动机法 (CA)对钢液凝固进行形核和生长计算.结果表明:电渣重熔钢锭凝固组织结构主要由柱状晶构成，在底部有一个垂直的柱状晶带，两边有一个延伸的倒V形柱状晶带.本文还考查了电极熔速、渣池温度等工艺参数对温度场的影响，以及平均形核过冷度和最大晶粒密度对微观组织的影响.模拟结果与低倍检测实验结果吻合较好.故可以据模拟结果调整制备工艺条件，获得具有理想凝固态组织的钢锭.

电渣重熔;数值模拟;微观组织;元胞自动机

电渣重熔工艺具有精炼提纯和定向凝固两重功能，电渣重熔原理图如图1，其优良的冶金反应条件和独特的结晶方式决定了其在模具钢、工具钢等合金结构钢领域具有不可替代的优势［1］.钢锭的凝固过程影响着最终产品的质量，对钢锭微观组织的模拟研究可以减少试验的成本和时间，为优化生产工艺提供依据.

在电渣重熔过程中，钢锭的传热行为直接影响着钢锭的结晶形态.钢锭内部温度场的分布，对于凝固质量起着决定性的作用.由于实验研究带来的高费用和测量的困难，数学模拟结合实验测试是分析钢锭工艺过程的一种有效方法.Ballantyne等［2］建立了考虑凝固潜热对温度场分布影响的数学模型，将数值结果与经验模型和实验数据对比分析，指出电渣重熔凝固模型进一步发展的必要性.Dilawari等［3］对渣池和金属熔池的流场进行了数值模拟，但他们对凝固过程没有涉及.Kelkar等［4］建立了二维轴对称综合数学模型，能够在耦合凝固情况下模拟渣池和金属液池流场和温度场.在国内，早在1980年傅杰等人［5］就实验研究了渣池温度分布对钢锭质量的影响.姜周华［6］通过热平衡方法对钢锭的温度场进行了模拟研究.陈元元等［7］对钢锭温度场做了动态模拟研究.耿茂鹏等［8］对渣池电位和温度场也进行了模拟计算.最近，Weber等［9］建立了电渣重熔的二维轴对称非稳态传热模型，计算了电磁耦合、流动传热和相变，并与实验结果进行了对比，熔池形状等吻合较好.迄今为止，国内外研究者对电渣重熔工艺过程中温度场、流场和电磁场的研究结果较丰富，而对微观组织的研究与模拟都很少.关于电渣重熔钢锭凝固组织计算目前仅见Nastac等人［10］用Monte Carlo法计算了合金718分别在电渣重熔钢锭的微观组织，但他只给出了晶粒生长方向，没有尺寸大小.尧军平等［11］借助MATLAB软件研究了小尺寸钢锭微观组织及不同冷却系数和渣池温度对微观组织的影响，只针对直径很小的钢锭(结晶器直径1.8 mm)凝固进行了研究，其凝固组织特性与通常电渣钢锭差别很大.

图1 电渣重熔原理图Fig.1 Schematic of Electroslag Remelting(ESR)

本文针对H13模具钢的电渣重熔钢锭凝固工艺，借助PROCAST软件，利用移动边界法研究钢锭枝晶生长及组织结构，建立电渣重熔工艺过程传热数学模型和凝固模型，以及晶粒形核和生长模型，采用元胞自动机法对电渣重熔钢锭的温度场和微观组织的形成过程进行数值模拟，考查了电极熔速、渣池温度等参数对电渣锭温度场的影响和形核过冷度、最大晶粒密度等参数对钢锭组织结构的影响.

1 数学物理模型

本模型采用的模拟结晶器直径为240 mm，成品锭高600 mm.在建模过程中作如下假设:

(1)在模拟过程中，由于金属熔滴和渣池的物理化学反应充分进行，假设渣池和金属熔池接触的渣金界面处温度相同.

(2)由于金属熔滴在下落过程中受到渣池的阻力，进入金属液池速度很小，故忽略金属熔池中流动对凝固的影响.

1.1 传热过程数学模型

式中Z，R，re分别为钢锭高度、半径和电极半径，Tslag为渣池温度，hsm，hb，hw分别是渣金界面、底部、侧面的对流换热系数.

1.2 形核与生长模型

Rappaz等［12］提出一种基于高斯分布的形核模型，假定形核现象发生在一系列不同的位置上，而这些形核位置可由连续而非离散的分布函数dn/d(ΔT')来描述.

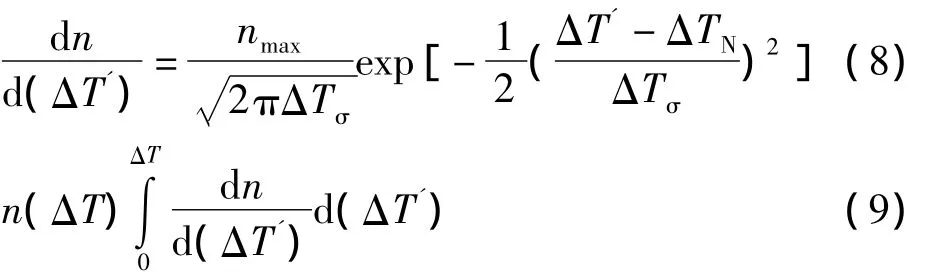
式中ΔTN是平均形核过冷度，ΔTσ是标准曲率过冷度，nmax是最大晶粒密度.

该模型忽略形核所需要的时间，当ΔT＜ΔTN时，随ΔT增大迅速地非线性增大;当 ΔT＞ΔTN时，随ΔT的增大迅速地非线性减小;当 ΔT=ΔTN时，达到最大值.ΔT时的晶核密度n(ΔT)则为dn/d(ΔT')在0～ΔT区域的积分值.因此，晶核密度随着过冷度的增大而由慢－快－慢的趋势连续增大.当过冷度足够大时，晶核密度可以达到最大晶粒密度nmax.

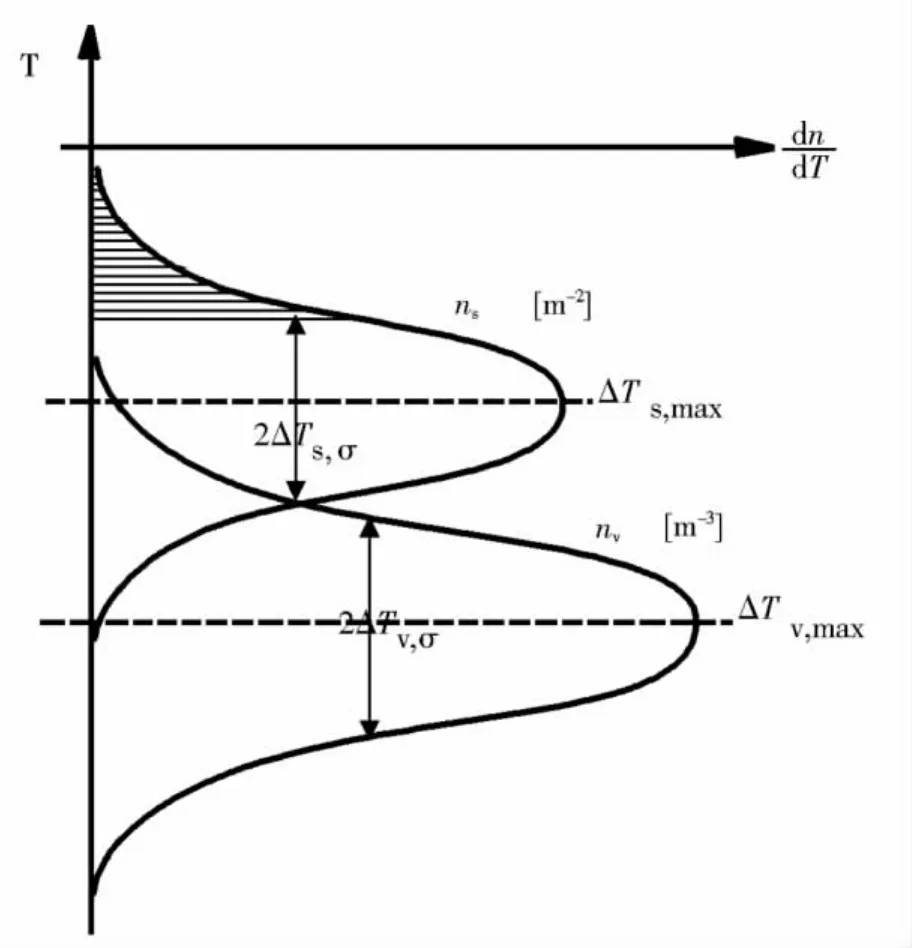
图2 形核高斯分布图Fig.2 Nucleation site distribution for nuclei formed at the mould wall

晶粒生长动力学采用了Rappaz和Kurz给出的 KGT(Kurz，Givoanola，Trivedi)简化模型［13］，枝晶尖端生长速率v与过冷度ΔT之间简化的关系式为:

其中，ΔTc、ΔTt、ΔTk、ΔTr分别为成分过冷度、热过冷度、动力学过冷度和曲率过冷度，后3个过冷度相对于成分过冷度较小，常可忽略.

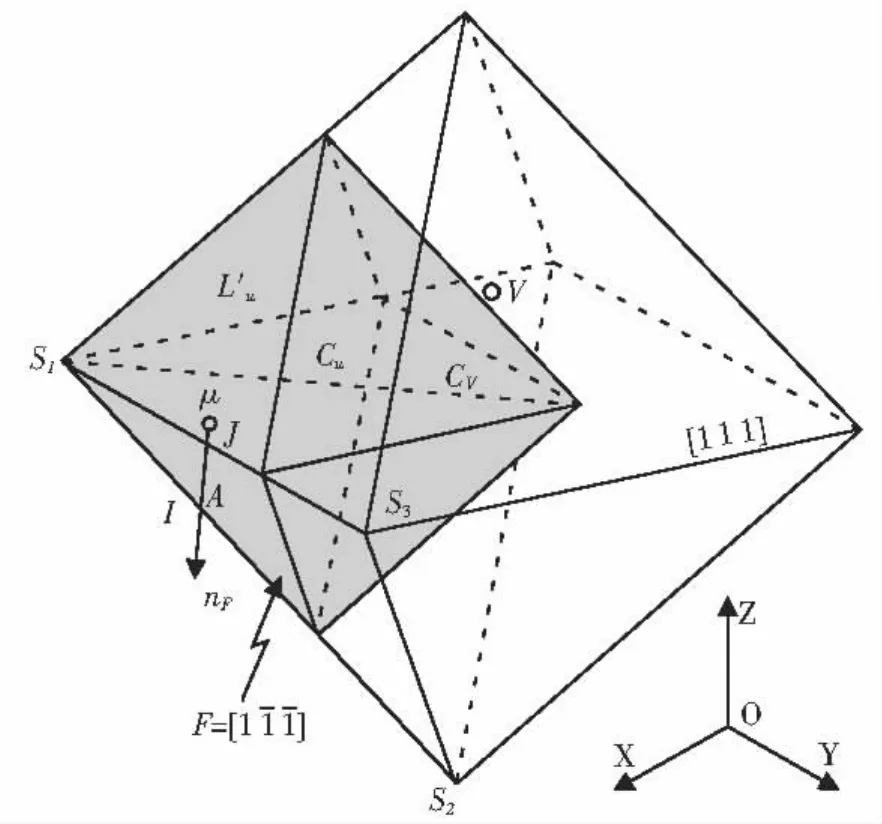
图3 正八面体元胞生长示意图Fig.3 Schematics of the decented octahedron CA growth algorithm and in the bulk of the liquid

晶粒的生长都是基于有限八面体的［111］面，每个生长的元胞被赋予非零的状态因子(Iυ≠0)计算，并且相邻元胞中至少有一个是液态.图3是包含元胞υ(Iυ≠0)的长大八面体正捕获一个相邻元胞μ(Iμ=0)的示意图.被捕获元胞μ的状态因子会转变为母元胞υ的状态因子(也就是Iμ=Iυ，即与母元胞保持相同的生长取向)，当包含元胞μ长大八面体完全被处于糊状区的元胞包围时便停止生长.八面体的主对角线方向对应＜100＞晶向，面心立方金属枝晶优先生长方向就沿着该方向.一个时间步δt内包含元胞υ八面体对角线的增量ΔRυ由下式给出［14］:

式中v(ΔTv)是元胞υ枝晶尖端的生长速度，它是过冷度ΔTv的函数.

1.3 CAFÉ 耦合模型

在CAFÉ－3D模型中，将有限元网格用于重熔过程的热计算，而将更加细密的规则方形网格用于CA计算晶粒组织，为了将FE和CA方法耦合到一个模型中，并且引入凝固潜热的影响，确保微观组织是温度场的函数，为此需要建立FE节点和CA元胞的关系.

图4显示了金属定向凝固原理，演示了柱状晶尖端的等轴晶和异质形核柱状晶的竞争生长及型璧拐角处树枝状晶的生长.模型划分的两种网格分别是典型的三角有限元(FE)网格(图4a)和CA模型中使用的元胞网格(图4b)，经过CAFÉ计算的柱状晶区域在图4b中由加粗的黑线表示.为建立宏观与微观的联系，定义了有限元网格节点和CA元胞之间的插值因子(图4c).在有限元网格I中心的CA元胞υ与有限元节点i、j、k之间分别具有非零的插值因子 Φυi、Φυj、Φυk.这些因子结合有限元节点的温度就可以确定网格中元胞处的温度.在节点处，采用同样的插值因子对树枝晶组织形核、生长过程释放的潜热求和，更新节点温度.

元胞υ在t时刻的温度和焓变可由下式插值可得［15］:

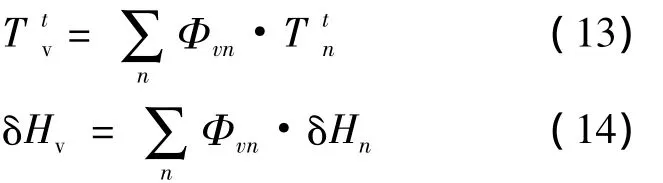
模拟计算过程中所使用到的液相线温度为1 473℃、固相线温度1 335℃、潜热260 kJ/kg、生长速度0.000 2 m/s、冷却水温度25℃、初始温度1 503℃，形核参数如表1所示.

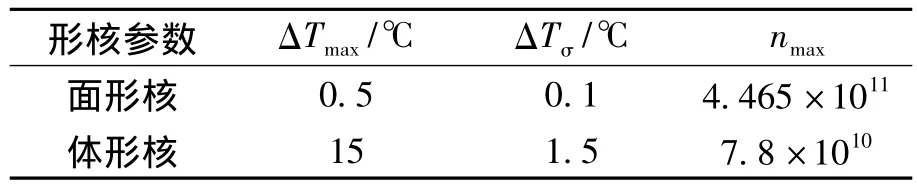
表1 钢锭组织结构计算输入参数Table 1 The input parameters for calculation of ingot grain microstructure

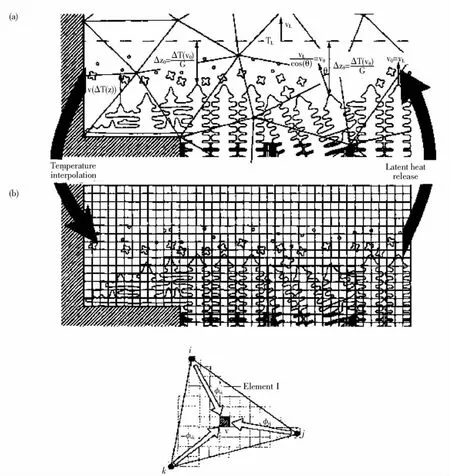
图4 有限元(FE)节点与元胞(CA)网格耦合关系示意图Fig.4 Schematics of the relationship between FE mesh and CA cells

2 结果 分析与讨论

由图5可知，电渣重熔过程中钢锭的温度自上而下均匀下降，熔池中部温度基本一致，边缘部位温度梯度较大，尤其是熔铸3 000 s时的钢锭温度场更为明显，在钢锭下部沿水平方向温度基本一致，这是由于结晶器和钢锭间形成的气隙起隔热作用，使得热量主要向底水箱方向传递所致.图6为电渣重熔凝固场分布图，在钢锭中部形成一个固液两相的交界区，上部为液相包括液态电渣和未凝固的液态金属，下部为凝固的金属，交界区内为固液两相混合区.开始时，钢锭高度较低，钢液的热量主要从底水箱传出，所以熔池很浅，等温线基本水平，随着电极的不断熔化，钢锭液面不断升高，熔池也逐渐加深(对比图6(a)和(b))，此时有较大一部分热量从侧面结晶器传出，到达某一高度时，熔池不会随电渣锭高度的增加而加深，图5和图6中(b)和(c)的熔池形状基本上没发生变化.

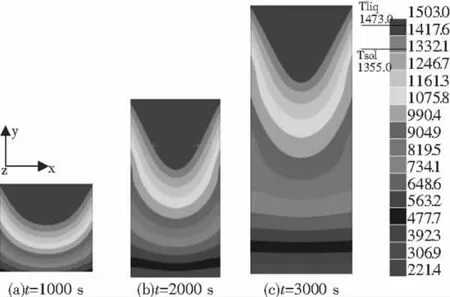
图5 电渣锭动态温度场分布图(单位:℃)Fig.5 The transient temperature distribution in ESR system

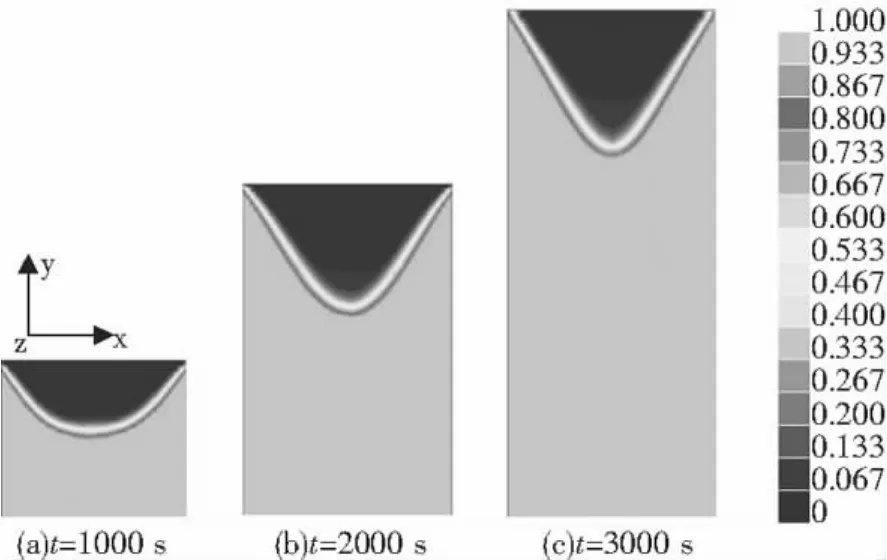
图6 电渣锭凝固场分布图Fig.6 The solidification distribution of ESR

对比图5(或图6)(a)图和(b)图发现，熔铸1 000 s到熔铸2 000 s过程中，熔池形状随钢锭高度的增长而发生明显变化，金属液池深度随钢锭升高不断增大.对比图5(或图6)(b)图和(c)图，熔铸2000 s到熔铸3 000 s过程中，熔池形状已不再随钢锭高度变化而变化，这就说明电渣重熔过程最终的熔铸速度与凝固速度将达到基本平衡.

由于钢锭与结晶器之间出现气隙，侧面采用了变化的传热系数，所以热流沿侧面并不是均匀分布，而是呈现出从上向下的递减趋势.(见图7)，钢锭侧面热流随与渣金界面距离的增加而减小，这与实际过程较为接近.采用电渣重熔法，以正常的熔速即可排除电渣锭中心部的等轴晶，形成柱状晶，而枝晶主轴间距和二次枝晶臂间距又非常小，所以大大降低了显微偏析，而使电渣锭组织精细，热加工性能优异，机械性能高且均匀，各向异性小.重熔开始时，钢水在底水箱的突然冷却作用下，底面起到了异质形核作用，如图8a底面所示.

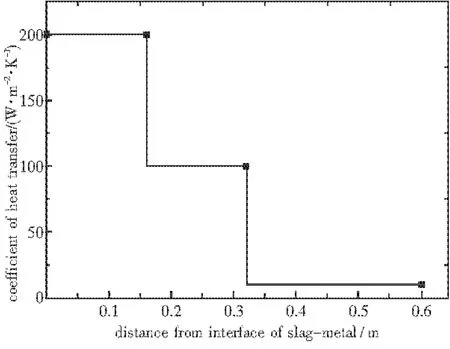
图7 电渣锭侧面传热系数分布图(单位:W/m2)Fig.7 The vector distribution of heat flux in ESR system

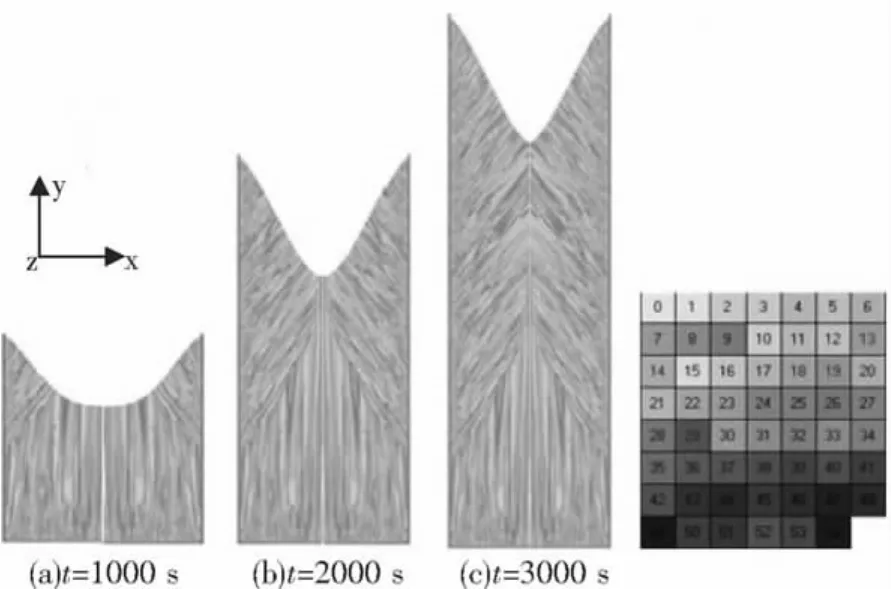
图8 电渣重熔钢锭微观组织形成过程Fig.8 The microstructure formation of ESR ingots

随着重熔工艺的进行，热量主要由底水箱传出，热流方向主要是向下的，见图7a，因此会在底面生成一个竖直的柱状晶区如图8a所示.当结晶器直径较大、熔化率较高时，在铸锭中部可能会有一些粗大的无定向等轴晶.对比图7和图8，由于电渣重熔法的热流定向性，纵向传热远远大于横向传热，热流方向为自上而下，而结晶生长的方向与热流的方向相反，即自下而上，和水平方向约成大于等于45(°)角，一直继续到锭的中心部.电渣钢铸锭的组织结构是在钢锭边缘有一层很薄的细小等轴晶带，在底部有一个垂直的柱状晶带，两边有一个延伸的柱状晶带，通常称为倒V形结晶，半面组织结构如图8.可以控制金属熔池呈扁平状，加大底水箱冷却强度，由此控制柱状晶趋于轴向生长.

晶体尺寸取决于晶核形成速率和晶核长大的线速度，这两者都是过冷度的函数，而这个函数关系是相当复杂的.在结晶过程中，过冷度越小晶核生成数目就会越多，晶核的长大也就越慢，就会得到致密的结晶组织.反之就会得到尺寸较大的组织.在电渣重熔过程中，为了细化结晶粒度，可以向结晶器中加入生核剂.电渣重熔能以高的温度梯度和低的生长速度进行定向的顺序凝固是与它较低的熔化速度有关的.当熔化速度过大时，金属熔池深度增加，同时结晶前沿附近的成分过冷区也相应增加，液相温度梯度降低.

钢锭不同高度横截面的微观组织如图9所示.钢锭的微观组织一般由两种结晶形态形成.当液态金属与冷的结晶器壁面接触后，在沿其表面的方向上，由于接触面吸热，使晶体的长大速度变快.此时，在指向液态金属内部的方向上的长大速度比较慢.在凝固初期，很快会形成一层凝固壳.凝固壳形成以后，传热强度最大的方向不是沿壁面方向，而是与壁面相垂直的方向，即热流方向.在热流方向上晶体生长最快，生长速度和热流速度正好相反.晶轴方向与热流方向平行的晶体，得到充分发展，沿热流方向平行的方向长得很长，成为柱状晶体.而那些优先生长方向与热流方向不平行的晶体得不到发展，只能是细小的等轴晶体，不能变成柱状晶体，见图9右侧的激冷层.

图9 电渣重熔钢锭横截面的微观组织Fig.9 The microstructure of the cross section in ESR ingot

本模型两个横截面的晶粒数、平均晶粒面积、最大晶粒面积和晶粒平均半径各参数如表1所示，晶粒数减少，晶粒平均半径增加.那些优先长大的晶体，除了在与热流平行的方向上发展其树枝状晶体外，由于侧向的成分过冷，在横向也会长出二次树枝状晶体.当二次树枝状晶体相碰时，又会在二次臂上长出平行于热流方向的三次树枝状晶体.柱状晶体的竞争长大不但表现在其形成的开始阶段，还表现在整个柱状晶体向前发展的过程中，柱状晶体的横断面尺寸不断竞争长大.

表2 模拟结果统计Table 2 Results statistics of simulation

图10为不同渣金界面温度对电渣重熔钢锭中心线温度的影响，其他参数不变.由图可以看出，初始温度为1 553℃时金属熔池最深，1 503℃时最浅，熔池随渣金界面温度的降低而变浅.电渣重熔过程中，电极在高温渣池中熔化成滴，金属液滴落入熔池的过程中不断与周围液态渣进行对流传热，由于渣池温度的升高导致渣金界面温度升高，钢锭中心处散热速度较慢，靠近结晶器的侧面的液体金属先凝固，此时侧面柱状晶生长快.相反，渣金界面温度较低，金属容易凝固，熔池变浅.

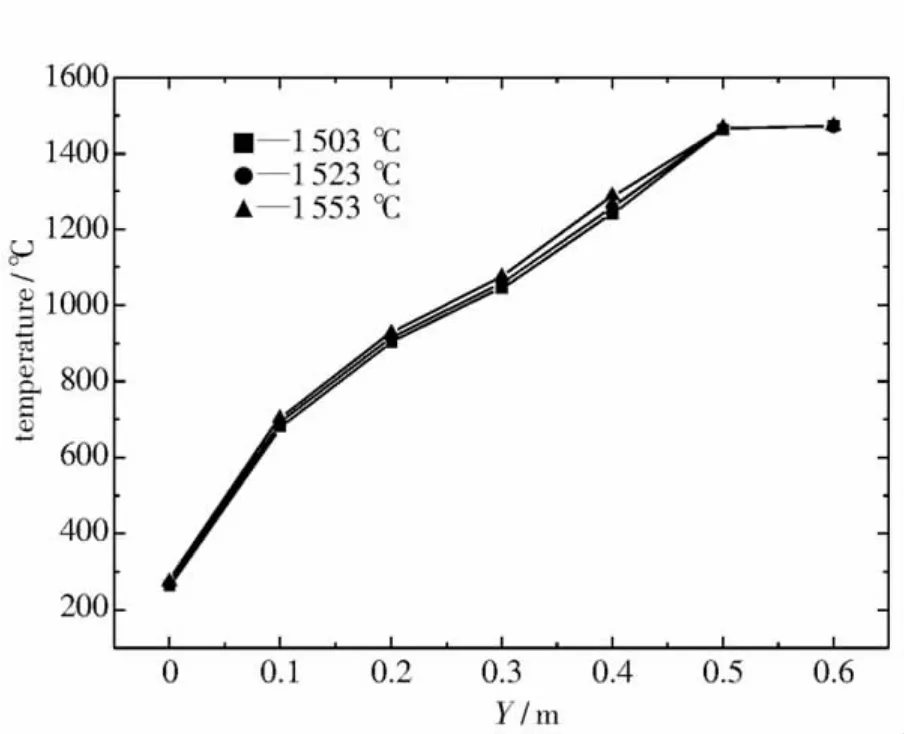
图10 渣金界面温度对钢锭中心线温度的影响(单位:℃)Fig.10 The effect of different slag/metal interface temperature on the temperature of centerline

图11为不同熔速对钢锭中心线温度的影响，由图可见，随着电极熔速增大渣金界上升面速度也相应增大，熔池深度增加并且熔池的凝固壳变薄，熔池尺寸变大.这是因为渣金界面上升较快，金属熔池中熔滴带来的热量相对也就越多，而其他条件没有发生变化，这使熔池内的热量不能及时传递出去，最终使得熔池变深变宽.

图12给出了不同体内形核过冷度的微观组织图，其他参数见表1，平均过冷度为10℃时，钢锭中心处没有等轴晶，随平均过冷度降低，等轴晶数量增加，柱状晶生长方向和尺寸大小基本没有变化，钢锭中心的等轴晶比侧面和底面的等轴晶尺寸差距很大，壁面处晶粒沿热流方向优先生长，故沿热流方向生长的晶粒在生长竞争中占有优势.

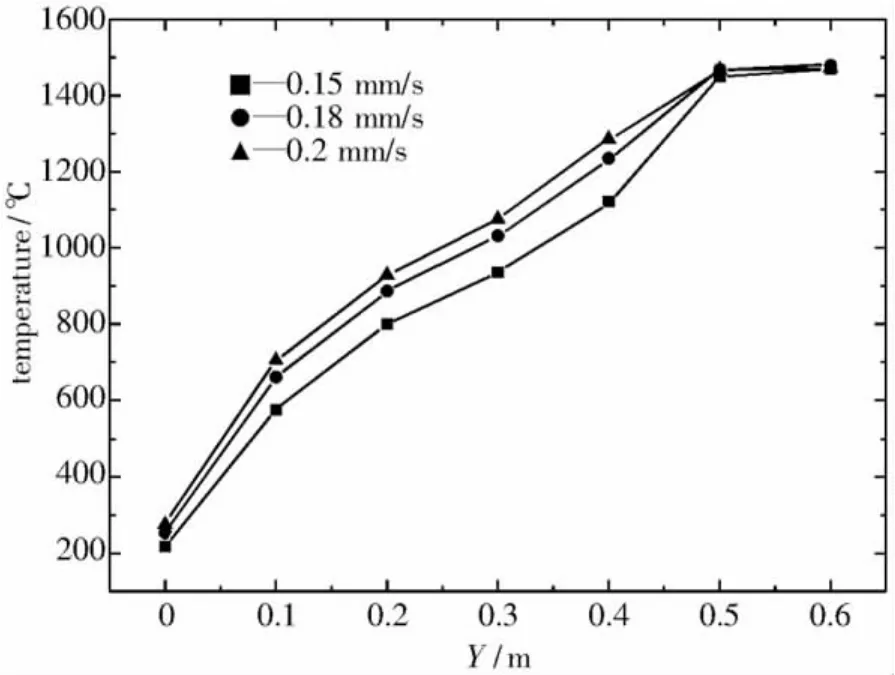
图11 不同熔速对钢锭中心线温度的影响(单位:℃)Fig.11 The effect of different remelting rate on the temperature of centerline

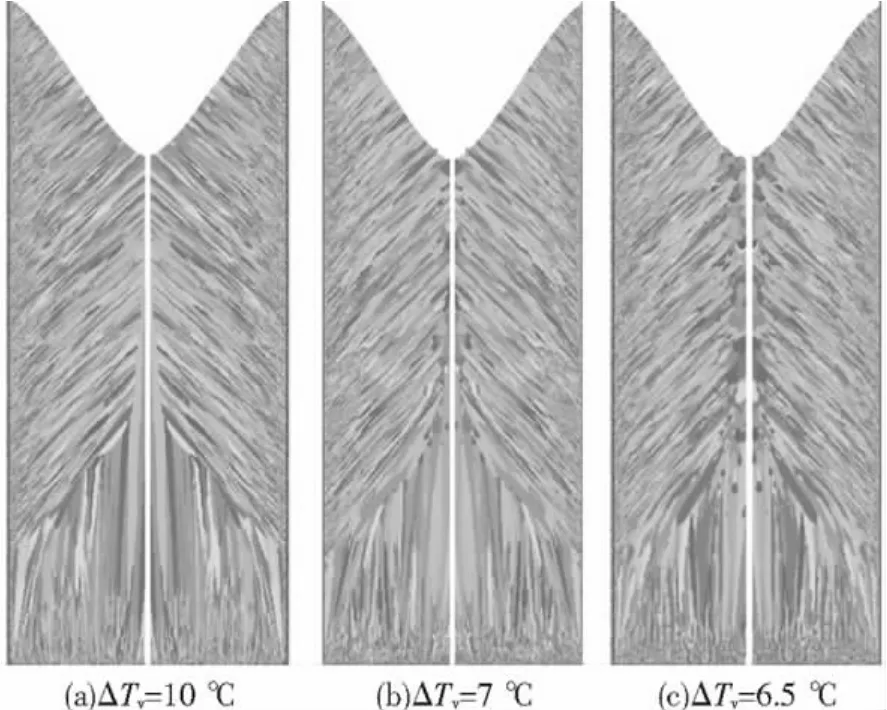
图12 体形核过冷度对微观组织的影响Fig.12 The microstructure with different mean undercooling in the bulk of the melt

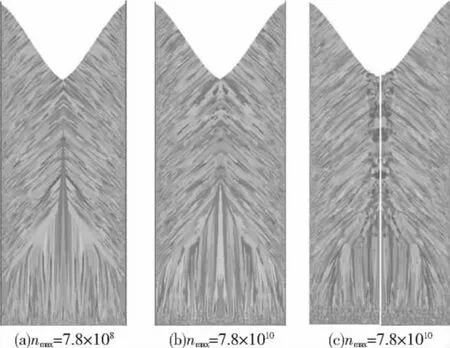
图13 最大晶粒密度对微观组织的影响Fig.13 The microstructure with different maximum grain density

当其他参数不变，最大形核晶粒密度发生变化时微观组织相应的变化如图13所示，底部等轴晶数量随最大晶粒密度的增大而增大，电渣钢锭中心处的等轴晶也越来越多，但尺寸明显比型壁处大很多，型壁处在激冷作用下大量非均质生核，发展成为大量等轴晶.

3 结论

(1)建立了电渣熔铸钢锭的温度场、凝固场数学模型，所得模拟结果与前人实验结果接近，证明了数学模型和边界条件的合理性.

(2)当钢锭高度达到一定程度，熔池深度不再随其高度增加而变化，即熔铸速度和凝固速度基本平衡，此时熔池深度和锭半径接近，直到重熔阶段结束.金属初始温度(渣池温度)升高或电极熔化速度降低都会导致金属熔池变浅，可使晶粒沿轴向生长的概率增加;反之，金属熔池变深，会使晶粒沿径向生长.

(3)建立了电渣重熔钢锭微观组织模拟的元胞自动机模型，利用ProCAST软件的CAFÉ模块，考虑了晶粒生长过程中形核位置和晶粒晶向的随机性，模拟了等轴晶向柱状晶的转变以及柱状晶的竞争生长.研究表明，降低平均形核过冷度和增加最大晶粒密度都可使电渣重熔钢锭中心部形成较大的等轴晶，在型壁处等轴晶密度也明显增大，根据这些结晶规律可以调整电渣重熔工艺参数获得理想凝固态组织.

［1］李正邦.电渣冶金原理及应用［M］.北京:冶金工业出版社，1996.

(LI Zheng－bang.Electricity principle and application of metallurgical slag［M］.Beijing:The metallurgical industry press，1996.)

［2］Ballantyne A S，Mitchell A.Modelling of ingot thermal fields in consumable electrode remelting processes［J］.Ironmaking and steelmaking，1977(4):222－239.

［3］Dilawari AH，Szekely J.A mathematical model of slag and metal flow in the ESR process［J］.Metallurgical and materials transactions B，1977，227－236.

［4］Kelkar K M，Patankar S V，Mitchell A.J Phys IV，2004，120:421－28.

［5］傅杰，陈恩普，陈崇禧，等.电渣重熔过程中渣池内的温度分布对冶金质量的影响［J］.金属学报，1981，17(4):394－401.

［6］姜周华.电渣冶金的物理化学及传输现象［M］.沈阳:东北大学出版社，2000.

(JIANG Zhou － hua.The metallurgicalslag electricity transmission and physicalchemistry phenomenon［M］.Shenyang:Northeastern university press，2000.)

［7］陈元元，刘喜海，李宝宽.电渣重熔钢锭凝固过程数学模拟软件［J］.钢铁研究学报，2005，17(6):30－33.(CHEN Yuan － yuan，LIU Xi － hai，LI Bao － kuan.Mathematical simulation software for solidification of electroslag remelting ingot［J］.Journal of iron and steel research，2005，17(6):30 －33.)

［8］耿茂鹏，孙达昕.电渣熔铸过程控制与模拟仿真［M］.北京:冶金工业出版社，2008.

(GENG Qing－peng，SUN Da－xin.The control and simulation of the electroslag casting process［M］.Beijing:The metallurgical industry press，2008.)

［9］Weber V，Jardy A，et al.A comprehensive model of the electroslag remelting process:description and validation ［J］.Metallurgical and materials transactions B，2009，40B:271－280.

［10］Nastac L，Sundarraj S，Yu KO，et al.The stochastic modeling of solidification structures in alloy 718 remelt ingots［J］.JOM(USA)，1998:30－35.

［11］尧军平，张磊，李海敏.电渣熔铸钢锭微观组织的模拟研究［J］.铸造技术，2008，29:1670－1673.

(YAO Jun－ping;ZHANG Lei;LI Hai－min.Simulation on the microstructure of electroslag remelting ingot［J］.Foundry technology，2008，29:1670 －1673.)

［12］Rappaz， Ch －A Gandian. Probabilistic modeling of microstructure formation in solidification processes［J］.Acta metall mater，1993，41:345－360.

［13］Kurz W，Giovanola B，Trivedi R.Theory of microstructural development during rapid solidification［J］.Acta metallurgica，1986，34(5):823－830.

［14］Gandin Ch－A，Rappaz M.A 3D cellular automaton algorithm for the prediction of dendritic grain growth［J］.Acta mater，1997，45(5):2187 －2195.

［15］Gandin Ch－A，Rappaz M.A coupled finite elementcellularautomaton model for the prediction of dendritic grain struc － ture in solidification processes［J］.Acta metall，1994，40(7):2233－2246.

The cellular automata model of electroslag remelting ingot structure

CHEN Ming－qiu1，LI Bao－kuan1，ZHAO Lin2

1.School of Materials＆Metallurgy，Northeastern University，Shenyang 110004，China;2.China First Heavy Industries，Fulaerji 161042，China)

A two－dimensional axisymmetric geometry which was established in this paper was divided into macrogrid finite element in order to compute temperature field;then grid was divided into more detailed and uniform cells，and at the last the continuous nucleation model based on the Gaussian distribution and KGT growth model was established for nucleation and growth calculations using cellular automaton method(CA)on the solidification of molten steel.The results show that:a vertical columnar grain zone and a inverted V － shaped columnar crystal zone appeared in the ESR ingot.In addition，the temperature field with different electrode melting rate and slag pool temperature parameters and the microstructure with different average nucleation undercooling and maximum grain density were studied in this paper.The simulation results agree well with the experimental results，so it is proved that the model and calculation method is reliable.To produce ideal solidified ingot and achieve the purpose of optimizing the production process，the production process was adjusted according to the simulation results.

electroslag remelting;numerical simulation;microstructure;cellular automata

TF 744

A

1671－6620(2011)S1－0130－08

2010－10－15.

国家技术研究与计划项目 (2007AA03Z556)，国家自然科学基金重点项目 (50934008)和上海宝钢集团联合资助.

陈明秋 (1986—)，男 ，山东日照人，东北大学硕士研究生，E－mail:libk@smm.neu.edu.cn.