区分度在中考试题质量分析中的应用

邹丽华

（大连教育学院 学习质量监测中心，辽宁 大连 116021）

区分度在中考试题质量分析中的应用

邹丽华＊

（大连教育学院 学习质量监测中心，辽宁 大连 116021）

阐述了区分度的内涵和作用，探讨了在经典测量理论和项目反应理论中三种常用区分度的计算方法及其应用。

中考试题；质量分析；区分度

根据对测验结果使用目的的不同，一般可以把测验划分为常模参照性测验和标准参照性测验。常模参照性测验的目的是对参加考试的考生进行挑选和选拔；标准参照性测验的目的是检测学生经过一段时间学习之后是否达到了学科课程标准要求掌握的基本知识和能力水平的程度。在我国高考、中考和会考等大规模考试中，高考是常模参照性测验，体现考试的选拔功能；中考和会考等属于标准化测验，但部分省市中考属于标准化测验和常模参照性测验（两考合一），兼顾学生学业水平考试和选拔两种功能。

区分度是定量分析试题质量的重要参数。测验目的不同，采用的区分度计算方法也不同。本文采用大连市2011年中考模拟考试数据，用三种方法对试题区分度进行计算，并对结果进行分析，以确定试题区分功能的类型。

一、区分度内涵分析

1．经典测量理论（CTT）下试题的区分度

区分度是指测验项目对被试心理品质水平差异的区分能力。［1］77区分度高的项目，能将不同水平的被试区分开来；区分度低的项目，则不能很好地鉴别被试水平。项目区分度也称之为项目的效度，它是评价项目质量、筛选项目的主要指标和依据。鉴别指数（D）是鉴别项目测量有效性的指标，D值越大，项目越有效。美国测量专家爱伯尔根据大量测量实践经验提出了用鉴别指数评价题目性能的标准。D值在0．4以上，认为试题很好；D值在0．30～0．39范围内，试题为良好，修改会更好；D值在0．20～0．29范围内，尚可，仍需要修改；0．19以下，试题劣，必须淘汰或加以修改。［2］243

用点二列相关法计算项目的相关系数需进行显著性检验，才能确定其意义。也可以根据相关系数的大小直接评价项目的区分性能，项目区分度评价标准见表1。［3］

表1 项目区分度评价标准

一般来说，试题的难度是相对的，同样试题区分度也具相对性，它体现在四个方面：不同的计算方法，所得区分度不同；样本容量大小影响区分度的大小；极端组划分的标准影响鉴别指数值（D），通常取27%作为分组标准；被试样本的同质性程度影响区分度的大小。因此，项目区分度的大小是相对特定团体而言的。［1］85

2．项目反应理论（IRT）下的项目区分度

在项目反应理论中，项目区分度与项目特征曲线拐点处的斜率有关。图1是三参数logistic模型项目特征曲线图。项目区分度ai表示项目i的区分度参数，它是曲线在拐点bi（项目难度）处切线的斜率。曲线在bi附近越陡峭，区分度ai值越大。当被试能力稍微偏离试题难度值时，被试正确作答项目的概率就迅速增大或变小，表现出很强的区分作用。

图1 项目反应理论下区分度参数的含义

在项目反应理论下，被试能力水平和项目难度在同一量尺上。模型拟合结果不仅可以估计项目参数（即难度、区分度），绘出项目特征曲线和信息函数曲线I（θ），还能估计出各被试的能力参数（θ）。项目参数与被试样本无关，被试的能力参数与项目无关。

二、区分度的作用

1．区分度影响测验的质量

衡量测验好与坏重要的统计指标是试卷的信度和效度。测验的信度与项目的区分度有着密切的关系。整个测验中各项目区分度的平均值越高，测验的信度就越高。因此，要保证测验达到较理想的测验信度，必须提高每个项目的区分度。一般大型考试试卷的信度在0．8以上才认为本次测验是有效的，否则就视为无效测验。因此，项目区分度对测验质量有着重要影响。

2．区分度影响测验项目的质量

测验项目区分度（ai）越大，伪机遇水平（ci）值越小，估计标准误就越小，测量就越准确。［4］在伪机遇水平一定的情况下，项目区分度的大小决定了该项目测量的准确程度。项目区分度越大就越能测出考生掌握的真实知识和能力水平。

3．确定项目的区分功能类型

在项目反应理论下，选择适当的参数拟合模型，对项目测量数据进行拟合，得到项目参数估值和项目特征曲线及信息函数曲线，据此可以对项目进行区分功能的细化，确定项目区分度功能类型。从项目特征曲线和信息函数曲线还可以得到有关试卷和试题统计结果方面的重要信息，如对什么能力水平的考生试题提供的区分度最大、提供的信息量最大，测量误差最小。

三、区分度计算方法

1．经典测量理论中的极端分组法

极端分组法是将学生能力按照测验总分排序，确定一定比例的高分组和低分组人数，然后根据高、低分组在某道题目上通过率或平均得分率的差值（D＝PH－PL，即该题鉴别指数）来衡量试题的优劣。该方法宜于理解，计算方便，但由于部分数据不参与计算而使计算结果不够准确，一般在教师自编测验中使用。

2．经典理论中的相关法

相关法是指以某一项目分数与效标分数或测验总分的相关作为该项目区分度的指标，相关越高，该项目区分度越高。［2］246常用方法有极差相关法、点二列相关法、二列相关法和Φ相关法等。由于中考试卷选择题居多，测验总分是连续变量，试题变量为真正的二分变量，应采用pearson点二列相关法。

用相关法可从两个角度对试题区分功能进行评价：一是依据相关系数评价题目性能标准（见表1）；二是对相关系数进行t检验，确定各题与总分的相关是否显著。用SPSS软件可直接计算出试题的相关系数，并同时显示试题与总分间的相关是否达到显著水平。样本相关系数的大小与选用样本大小有关，选用大样本计算试题相关系数，各试题与总分的相关性往往呈现显著水平。

3．项目反应理论中的极大似然法

极大似然法是使已知反应模式的似然函数值达到最大，是对未知参数估计的一种重要方法。项目反应理论下区分度参数的估计较经典测量理论下区分度的计算要复杂得多。参数估计需要众多数学模型、较多的参数估计方法及特殊应用软件的支持。在项目反应理论中，二值评分项目的单维基础模型有双参正态肩形曲线模型、拉希模型和罗杰斯蒂（Logistic）模型；多值评分项目的单维模型有称名选项模型、等级反应模型和部分评分模型。

四、计算结果分析

以大连市2011年中考物理模拟考试成绩为样本（样本容量为16146），用极端分组法和点二列相关法计算区分度，用三参数Logistic部分评分模型，使用PARSCAL4．1软件，采用牛顿极大似然法（ML）和Partial分步评分模型进行项目参数估计，同时做先验分布检验。其结果包括估计项目难度、区分度、信息量等项目参数及被试能力参数。模型参数估计的最后拟合指数为－2 LOG LIKELIHOOD＝687824．238。三种方法计算结果见表2。表2中第2～5列分别显示各题目的难度系数、鉴别指数（D）、各题与总分的相关系数（rpb）及相关程度，第6和7列呈现的是用极大似然法得到的项目参数估计值。

1．从经典测量理论角度分析

由表2第3列数据可知，试题鉴别指数范围在0．05～0．66，第3题的鉴别指数最小，第9题的鉴别指数最大，主观题第28、30题鉴别指数小于0．19，试题对考生能力的区分程度较差。按鉴别指数评价试题性能标准，有29%的试题为劣质试题。显然对于标准参照考试，用鉴别指数评价试题质量的好坏不公平。极端分组法尤其不适用于标准参照考试中客观题区分度的计算。

由表2第3和4列可知，用Person点二列相关方法计算区分度与用极端分组法计算鉴别指数是不等值的，差值有大有小，且各试题的相关系数大于鉴别指数。如第1题r＝0．31，D＝0．05。

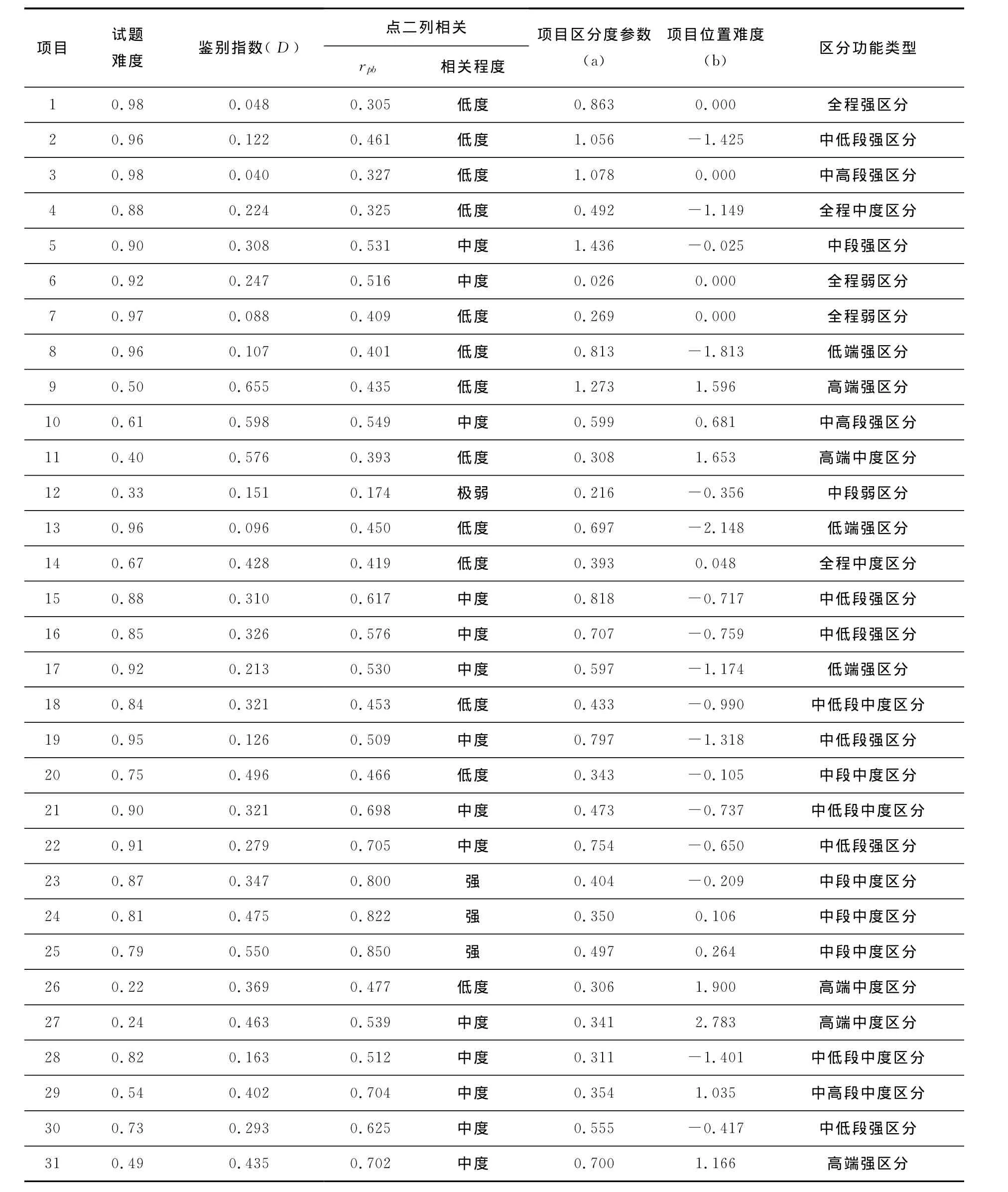
表2 项目区分度

从表2第4列数据看，相关系数范围从0．17到0．85。试题与总分的相关程度：有3道题是高度相关，24道题是中度相关，12道题是低度相关，1题（第12题）是弱相关，它们分别占总题量的9．68%、45．16%、41．94%和3．23%。第12题与总分几乎不相关，第25题对考生的区分程度最高。而用点二列相关t检验的结果：物理试卷31个项目与总分相关，都呈显著性水平（P＜0．05），表明所有项目与总分间都有很好的内部一致性。

2．从项目反应理论角度分析

项目难度和区分度参数估计结果见表2第6列和第7列。以项目5为例，图2和图3分别是项目5的特征曲线和信息函数曲线。项目5的区分度参数a＝1．436，难度参数b＝－0．025，猜测概率c＝0．406。通过计算可得出：当被试能力θmax＝0．149时，项目5提供的信息量I（θ）最大，I（θ）＝0．67。项目5的低能力被试答对的可能性（c＝0．406）不为0，猜测度偏高。

按项目区分度参数估值大小划分项目区分性能。项目区分度a＜0．30，认为是弱区分项目；0．30≤a＜0．50项目为中度区分，a≥0．50认为项目是强区分。根据项目5的项目参数和项目特征曲线，同一项目对不同能力水平的被试试题提供的区分程度是不同的。对能力水平约在－1．0～1．2范围内的考生都有一定的区分，对能力水平处于0．149的考生区分能力最强。因此，该项目区分类型是属于中段强区分项目。其他项目的区分类型见表2中第8列所示。

从表2中数据可知，项目区分度参数a≥0．50的强区分项目有15个，占总题量的48．4%，其中第9、31题属于难题，其他试题属于中档题和容易题；中度区分的项目有13个，占总题量的41．9%，其中第11、26、27题属于难题；a＜0．30的弱区分项目有3个，即第6、7、12题，其中第6、7题属于容易题，第12题属于难题。

五、区分度应用需注意的问题

1．正确认识区分度指标要求

对项目区分度指标的要求应根据测验目的而定，若测验目的在于选拔，主要评判被试的个别差异，那么区分度要求高一些；若测验只是考察被试对所学知识的掌握情况，就不用过多地考虑区分度。对于兼顾上述两个目的的测验，虽然对大部分试题区分度没有要求，但对承载选拔功能试题区分度的要求要高些。

2．恰当选择区分度计算方法

在实际项目质量分析中采用何种区分方法，应根据测验目的以及项目记分和测验总分两个变量的性质。方法不同，试题区分功能评价标准及结果也不同，有时也可以同时使用不同方法相互验证，确保统计分析结果的实效性和准确性。

3．合理运用项目区分功能类型

细化项目区分功能类型是对项目的综合评价，它给出某一项目适合考查什么样能力水平的被试，区分是强区分、弱区分还是中度区分。根据试题区分功能类型可对项目进行筛选、修改，挑选合适的题目组成试卷，为试题进行等值研究和题库建设等提供技术支持。

［1］戴海崎，张锋，陈雪枫．心理与教育测量［M］．广州：暨南大学出版社，2010．

［2］朱德全，宋乃庆．现代教育统计与测评技术［M］．重庆：西南师范大学出版社，1998．

［3］王力宾．多元统计分析：模型、案例及SPSS应用［M］．北京：经济科学出版社，2010：31．

［4］漆书青，戴海琦，丁树良．现代教育与心理测量学原理［M］．北京：高等教育出版社，2002：159．

On Effect of Differentiation Index in Quality Analysis of High School Entrance Examination Questions

ZOU Li－hua
（StudyQualityMonitoringCenter，DalianEducationUniversity，Dalian116021，China）

Expounding the effect and connotation of differentiation index，the paper discusses calculating methods and application of three common differentiation indexes in classical testing theory and item response theory．

high school entrance examination question；quality analysis；differentiation index

G424．79 < class="emphasis_bold">文献标识码：A文章编号：

1008－388X（2011）04－0027－04

2011－09－30

本文为辽宁省教育科学“十二五”规划课题“初中终结性考试学科难度常模构建及应用研究”（JG11CB052）阶段性研究成果。

邹丽华（1963－），女，吉林吉林人，中学高级教师。

阅力］