连铸板坯凝固过程的数值模拟

徐 东，赵红阳，卢艳青

(1.东北大学材料与冶金学院，沈阳110819，E-mail:xudong_xyz@163.com; 2.辽宁科技大学材料科学与工程学院，辽宁鞍山114051)

连铸板坯凝固过程的数值模拟

徐 东1，赵红阳2，卢艳青2

(1.东北大学材料与冶金学院，沈阳110819，E-mail:xudong_xyz@163.com; 2.辽宁科技大学材料科学与工程学院，辽宁鞍山114051)

为得到连铸坯凝固末端的液相穴分布，以便选取轻压下参数，依据实际生产中二冷边界换热条件，采用有限元法对连铸厚板坯冷却传热过程进行数值模拟，并用远红外测温仪测试并校准Q235B300 mm× 1650 mm铸坯表面温度，得到了连铸坯在任意段截面的温度场分布、凝固末端液相穴形状及铸坯中心纵截面固相率分布.结果表明，可以根据铸机实际情况，在距液面17.6～23.7 m处选取合适的轻压下参数.

厚板坯;温度场;二次冷却;数值模拟

铸坯在二冷区凝固末端的位置及其液穴形状是连铸过程中的一个重要参数，目前国内外许多研究者都采用凝固末端轻压下技术改善连铸坯的偏析问题［1］，确定了凝固末端位置及其液穴形状，将为轻压下位置的选定提供参数［2］.连铸坯凝固末端位置的确定方法有实验测定法和数值模拟法等.数值模拟法具有费用低、速度快、精度高、可模拟极限情况及能得到更为完整的信息资料等优点，而且连铸板坯的工作条件和现场环境决定了其他方法研究存在着诸多局限.

本研究工作结合厚板坯连铸机的实际工作情况，用有限元法来预测板坯凝固末端位置及其液穴形状.由于厚板坯凝固末端坯壳较厚且液相较少，试验无法直接清晰地测出末端液穴形状，在本文中用红外测温仪测出板坯表面各部分温度，将模拟所得结果与测量结果进行对比，间接验证了模拟的液穴形状及位置.

1 数学模型

1.1 凝固传热数学模型的基本假设

为简化方程及其边界条件，作如下假设:l)将液相的对流现象归为导热问题;2)假设刚进人结晶器的钢液温度与浇铸温度相同;3)铸坯内弧和外弧传热条件对称;4)连铸机内同一冷却区里水量分布均匀;5)忽略沿拉坯方向上的传热.

1.2 能量守恒方程

传热过程的能量控制守恒方程如下［3］:

式中:θ为温度，℃;t为凝固时间，s;ρ为材料密度，kg/m3;cp为材料定压比热容，J/(kg·K);k为导热系数，W/(m·K);G为凝固潜热项.

1.3 有限元模型建立

本研究所选对象为一炼钢的直弧型厚板坯连铸机，铸坯厚度 300mm，最大浇注速度1.6 m/min.此连铸机的常规拉速为 0.6～1.4 m/min，冶金长度为33010 mm，二冷段含8个冷却区，15个控制回路，各区内喷嘴喷水一致，足辊区为全水冷，其余为气－水雾化冷却.

本文以拉坯方向的垂直铸坯横截面作为研究对象，其铸坯几何尺寸为:宽度1650 mm，厚度300 mm.因为铸坯截面为中心轴对称，本文中取1/4截面作为建模区域.

1.4 导热系数的处理

固相区:0～1200℃温度，使用《连续铸钢手册》［4］里的热导率，1200℃到固相区的导热系数取29.4 W/(m·℃).

液相区:在结晶器中取固相区的6倍，二次冷却区取固相区的2.5倍［5］.固液两相区:导热系数是由液相和固相的比例加权得到的.

1.5 比热和固相率(fs)的确定

在本文中Q235B在固相区的比热取值为670 J/(kg·℃)，在液相区的比热取值为840 J/(kg·℃)［6］.液固两相区进行插值处理.

固相率(fs)的表达式如下:

其他相关热物性参数见表1.

表1 Q235B热物性参数［6］

1.6 初始条件和边界条件

初始条件:浇铸温度为1537℃.边界条件包括:

(1)在结晶器内，铸坯表面导出热量等于一冷水带走热流量.

(2)在二冷喷水冷却区，铸坯表面导出热流(h)与二冷水流量(fw)及铸坯表面温度(Tb)有如下关系［7］:

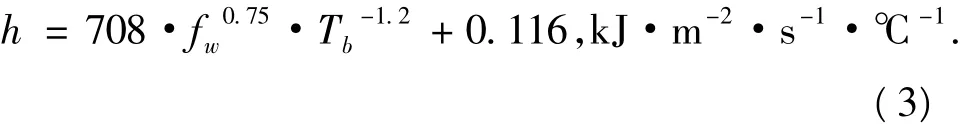
(3)在二冷气雾区，铸坯表面导出热流(h)与二冷水流量(fw)及空气流量密度fa有如下关系［6］:

(4)在空冷区，主要是板坯侧面及喷淋不到的表面，靠辐射带走热量［6］:

1.7 有效喷淋面积的计算

为了准确模拟温度场在横截面上的分布，本文根据实际喷嘴喷射角度计算出有效喷淋面积如表2所示.图1为该铸机6区喷嘴实际分布图，由图可以计算出6区有效喷淋面积，可以得到更准确的换热系数.

(1)区域h1，相邻的2个喷嘴都能喷到，使用计算出的换热系数;

(2)区域h2，只有单个喷嘴能喷到，使用区域h1换热系数的0.8倍;

(3)区域h3，喷水区外，由于该区域喷水量较小或没有喷水量，采用自然对流及辐射放热来计算.

对于另外几个冷却区也按同样的方法计算.

表2 各冷却区喷嘴分布

图1 6区喷嘴换热系数计算分布图

1.8 二冷区气水分布参数

二冷区气水分布参数见表3.

表3 Q235B钢二冷区气水参数

2 表面测温实验

本试验所用铸坯表面辐射测温装置主要由两部分组成，即XDW－1型棱镜分光单色红外测温仪和ZTQ－1型智能显示调解器.测温试验在连铸机正常生产的条件下进行，在一个浇次时间内，测温时拉速恒定，在同一位置认为温度不随时间变化.每0.5 s显示一组温度数据信号，共记录10组数据.由于铸机条件所限，测温从第六扇形段开始，一直到铸坯出矫直区的每个扇形段的出口处.由于测温数据较多，测温过程及数据见文献［8］.

图2 XDW-1棱镜分光红外测温仪

测温试验主要针对板坯内弧表面，由于铸坯内弧面冷却对称，所以本试验只测取了内弧表面的一半.横向位置选择在铸坯内弧侧的1/2、1/4、1/8处以及距边缘30～10 mm的边部部位.

表4 部分测温试验数据

3 结果分析与讨论

3.1 铸坯冷却温度变化分析

在拉坯速度0.79 m/min、过热度24℃条件下的铸坯距窄面1/2处，铸坯表面、中心及表面下30和50 mm处各点的温度变化如图3所示.由图3可知:距窄面1/2处，铸坯表面温度在一段末端达到最低758℃，然后温度波动上升到900℃左右，此后大致在800～900℃内波动;由曲线d可见，铸坯中心固液转变点在23.2 m处;8区末端，中心温度为1204℃，表面温度为864℃.模拟计算与实测表面温度基本一致.

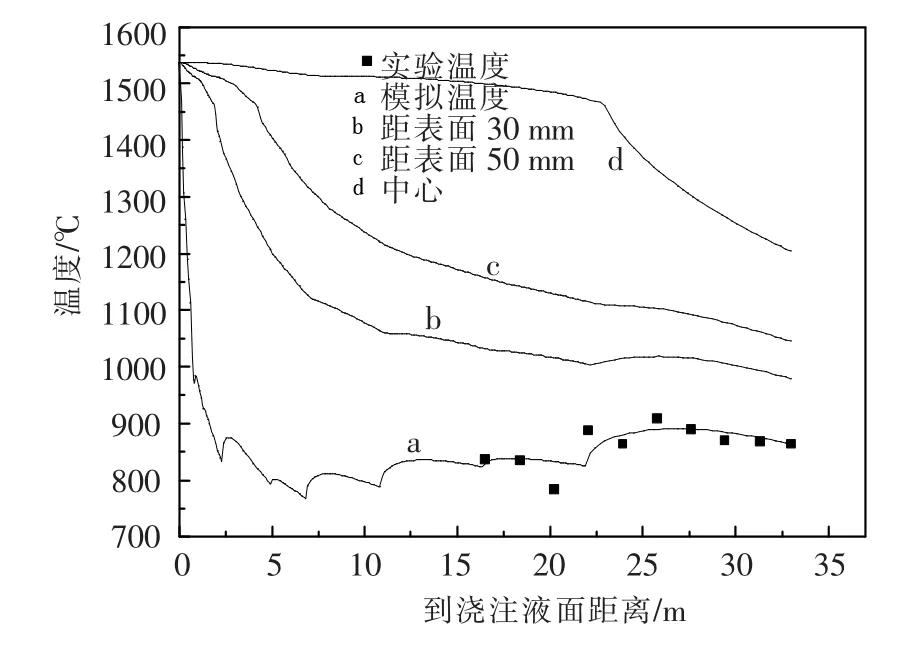
图3 距窄面1/2处(即宽面中心处)各节点的温度分布

距窄面1/8处，铸坯温度场分布如图4所示.从图4可以看到，铸坯表面温度在二冷区2区末端达到最低831℃，然后温度波动上升到958℃，之后温度大致在900～950℃内波动;由曲线d可见，铸坯中心固液转变点在24.3 m处;8区末端，中心温度为1205℃，表面温度为908℃.由曲线a可见，模拟计算与实测表面温度基本一致.

由于实际在距窄面30～10 mm的地方进行边部测温，所以使用距窄面15 mm处的节点为边部模拟值，具体见图5.从图中曲线a可见，铸坯表面温度在2区末端达到最低894℃，然后温度快速上升到1058℃，此后温度缓慢下降到830℃左右;铸坯中心液相在结晶器就已经全部凝固成固相，之后缓慢下降;8区末端，中心温度为940℃左右，表面温度为780℃左右.模拟计算与实测表面温度基本一致.

3.2 铸坯截面液相穴分布

连铸坯拉速为0.79 m/min、过热度为24℃时，铸坯凝固末端液相穴形状在横截面上的分布见图6.1513℃为液相线，以上为液相区和液固两相区.

图4 距窄面1/8处各节点的温度分布

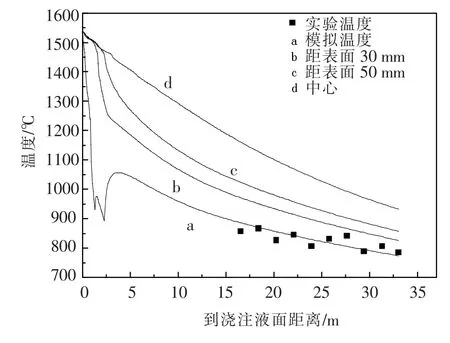
图5 距窄面15 mm处的各节点温度分布

图6 凝固末端液穴分布图

根据固相率，两相区可分为裂纹敏感区及液相填充区［9］.不同的钢种及工艺条件有不同的临界固相率，一般认为临界固相率为0.8～1［10－11］.由于板坯轻压下位置的选定与铸坯的凝固状态有关，由于板坯轻压下一般选在固相率为0.3～0.8的区域［12－13］，根据固相率与温度的关系式，可以得到铸坯中心纵截面固相率分布图，如图7所示.

由图6和7可以看出:板坯连铸凝固过程中，板坯的最高温度不在板坯中心处，而是在距窄面1/8处，当铸坯中心凝固时，距窄面1/8处仍处于固液两相区.

距窄面 1/2处，铸坯中心固相转变点在23.2 m处，在17.6 m处板坯中心固相率达到0.3，在22.6 m处板坯中心固相率达到0.8.

距窄面 1/8处，铸坯中心固相转变点在24.3 m处，在18.2 m处板坯中心固相率达到0.3，在23.7 m处板坯中心固相率达到0.8.当这样为我们制定板坯轻压下工艺参数提供依据.

图7 铸坯中心纵截面固相率分布

4 结论

1)对比模拟计算结果与现场测温结果，二者变化趋势基本一致.

2)距窄面1/2、1/8处，铸坯中心固相转变点分别在在23.2、24.3 m处，转变点后移1.1 m.

3)距窄面1/2、1/8处，分别在17.6、18.2 m处板坯中心固相率达到0.3，后移0.6 m;分别在22.6、23.7 m处板坯中心固相率达到0.8，后移1.1 m.

4)凝固末端液穴形状的变化为厚板坯轻压下提供依据，根据凝固图，轻压下应选在17.6～23.7 m处，轻压下如果选择过于靠前或靠后，不但无法减轻偏析，还有可能造成内部裂纹.

［1］钟华杲.连铸坯液相穴末端轻压下技术的发展［J］.国外钢铁，1991(11):26－33.

［2］干勇，陈栋梁.薄板坯连铸液芯压下过程的数值仿真［J］.钢铁，1999，34(6):27－31.

［3］金学伟，王长松，张玉宝，等.基于有限元的板坯连铸凝固过程数值模拟［J］.冶金能源，2009，28(3):23－24.

［4］陈家祥.连续铸钢手册［M］.北京:冶金工业出版社，1991.

［5］阮晓明，阎朝红，梅峰，等.宝钢板坯连铸凝固与传热模型的开发［J］.连铸，2009，162(3):21－24.

［6］贺道中.连续铸钢［M］.北京:冶金工业出版社，2007.

［7］史宸兴.实用连铸冶金技术［M］.北京:冶金工业出版社，1998.

［8］徐东.板坯连铸二冷区模拟研究［D］.鞍山:辽宁科技大学，2010.

［9］蔡正，王国栋，刘相华.热轧带钢温度场的数值模拟［J］.金属成形工艺，1998，16(5):39－42.

［10］日本钢铁协会编.王国栋，吴国良，译.板带轧制理论与实践［M］.北京:中国铁道出版社，1990.

［11］PATANKAR S V.Numerical heat transfer and fluid flow，hemi-sphere［M］.New York:John Benjamins Publishing Co，1980.

［12］OHK S，PARK J K，CHANG S H，et al.Development of soft reduction technique for the bloom caster at Pohang Works of Posco［C］//Steelmaking Conference Proceedings，Pohang:［s.n.］，1995:301－308.

［13］祭程.板坯连铸动态二冷与动态轻压下过程控制系统的开发与应用研究［D］.沈阳:东北大学，2007.

Numerical simulation of solidification process of continuous casting slab

XU Dong1，ZHAO Hong-yan2，LU Yan-qing2
(1.School of Materials and Metallurgy，Northeastern University，Shenyang 110819，China，E-mail:xudong－xyz@163.com; 2.School of Materials Science and Engineering，University of Science and Technology LiaoNing，Anshan 114051，China)

To get the distribution of liquid core in the end of solidification，and to select the soft reduction parameters，considering the boundary conditions for secondary cooling of heat transfer on actual production，a mathematical model for thermal transmission to suit slab caster has been established.According to the surface temperature of 300 mm×1650 mm slab of Q235B steel measured by using infrared thermo scope，the temperature distributions at any casting section，the distribution of liquid core in the end of solidification and the distribution of fraction solid on longitudinal section of slab center have been obtained.It is shown that the soft reduction parameters can be selected at 17.6～23.7 m of liquid surface.

slab continuous casting;temperature field;secondary cooling;numerical simulation

TF777 文献标志码：A 文章编号：1005－0299(2011)05－0106－05

2010－11－22.

徐 东(1984－)，男，博士研究生;

赵红阳(1971－)，男，教授.

(编辑 程利冬)