强旋薄壁管材z-θ向残余剪应力的测量方法

张 振，苏国跃

(中国科学院金属研究所，沈阳110086，E-mail:zzhang@imr.ac.cn)

强旋薄壁管材z-θ向残余剪应力的测量方法

张 振，苏国跃

(中国科学院金属研究所，沈阳110086，E-mail:zzhang@imr.ac.cn)

为建立旋压薄壁管材残余剪切应力的测量方法，并估算强旋2024Al样品管的残余应力，沿单侧纵向切开管段并测量了变形.对变形进行简化的基础上，以弹性力学方法推导出了残余剪切应力的算式，并计算了样品管材的残余应力大小.结果表明：样品管材存在显著的z－θ向残余剪切应力，应力的大小与切口两侧的轴向错开量成正比，应力沿壁厚的分布接近线性，最大值位于管材内表面;本文建立的方法，可用于测量旋压管材的z－θ向剪切残余应力.

强旋;管材;残余剪切应力

强力旋压制备管材时，变形区呈点状，运动轨迹为螺旋线，其变形不满足轴对称条件，此时形成的残余应力不仅包括沿坐标方向的正应力、轴向的剪切应力，还应包圆周方向的剪切应力［1］.估算薄壁管材周向残余正应力［2－3］和轴向残余正应力［4］的近似测量法，已广泛应用［5－11］.强旋管材沿轴向切开后断口两侧相互错开［11］、取轴向管剖条时出现侧弯［12］都表明残余剪切应力的存在，但尚没有残余剪切应力的估算方法.

本文根据旋压管材切开后剪切变形的特点，应用弹性力学建立了表面残余剪切应力与变形的定量关系，并据此求得所制管材的残余剪切应力，并分析了产生的原因.

1 实验

对强旋2024Al—Φ 115×1.7薄壁管材，在电火花线切割机上分别切取高度为 2、10和20 mm的管段.以细针在管段外壁刻三细线，如图1所示，并以分辨率为0.01 mm的读数显微镜读取两竖直刻线间距.在两刻线间沿纵向切开一侧管壁后样品变形，再读取水平刻线错开量、竖直两刻线的间距变化.

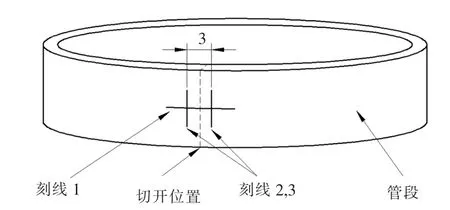
图1 样品刻线方式

2 结果

不同高度样品切开后均出现明显的轴向错开，变为螺旋状，如图2所示.以刻线1在切口两侧的间距表征轴向错开量δ，刻线2、3在切开前后的间距变化表征周向张开量Δ，样品的变形测量结果见表1.

图2 强旋管材三段样品纵切后的变形

表1 实验管段的变形

由结果可见，切开后切口两侧出现轴向错开和周向重叠，并且轴向错开量远大于周向重叠量.不同高度样品的轴向错开量有一定差异，但差异不大.

3 应力分析

样品变形是切口后残余应力释放的结果，其中周向重叠与周向残余应力释放有关，应力最大值可根据重叠量Δ，由文献［5］中的Crampton法计算式的导出式进行估算.文献［5］中给出的Crampton法计算式为

式中:Di、Df分别为切口前、后管材的平均外径;t为管材壁厚;E为材料弹性模量;v为材料泊松比.

对薄壁管，当周向重叠量不大时，Di≈Df，则式(1)可简化为

由本式计算试验管材的最大周向残余应力，取模量为72.4 GPa时，各样品的计算值为8.32～10.96 MPa.

而切口两侧轴向错开与剪切残余应力释放有关.下面以弹性力学方法，建立残余剪切应力与轴向错开变形的关系.

3.1 模型与坐标系建立

设样品残余应力因切口两侧轴向错开δw而完全释放，处于无应力状态.此状态作为分析的起始状态.

按照图3所示建立坐标系，并设u、v、w分别为径向、周向和轴向的位移.

图3 应力释放圆环及坐标系

设此错位环在某力作用下变形至两断口对合，并粘接在一起.此时管材内应力自相平衡，此内应力与待计算的残余应力相等.在这一过程中材料发生弹性变形，而薄壁管材的变形满足以下3点假设［13］:

1)薄壁假设:管材厚度(t)与中面半径(R)相比甚小，即＜＜1;

2)小变形假设:轴向错开量与周长相比很小，即在几何方程中的二阶项与高阶项均可以略去;

3)变形的正交性假设:管壁中面的法线在变形后依然与中面正交;管壁的法向线元在变形过程中保持直线且不发生伸长或缩短.

3.2 基本方程

圆环由无应力的错开状态合并粘接后，圆环内产生自相平衡的残余应力，此应力满足平衡方程(不考虑体积力)

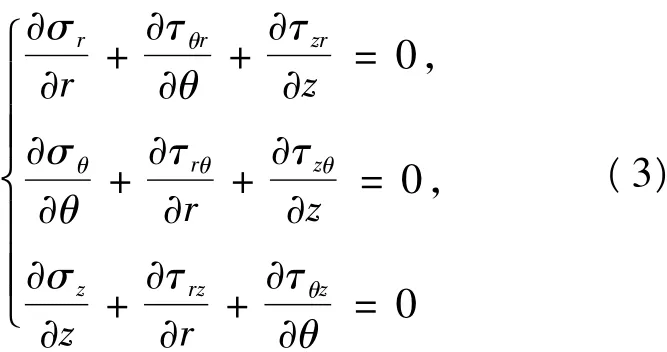
式(3)为三元弹性微分方程，直接计算无法求得解析解.弹塑性问题求解关键在于问题的合理简化和正确给定边界条件.现根据实际变形特点，对边界条件进行简化.

3.3 位移边界条件

试验结果表明样品高度对轴向错开变形影响不大，可假定不存在边界效应.由此，可对位移边界条件进行如下简化

1)变形前后管段没有径向张缩，即u=0;

2)切口闭合前后两断口间有轴向错位δw，即沿管一周上升δw，则z向位移可表示为

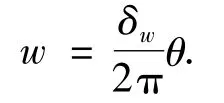
3)虽然v未知，但由于环在闭合后呈几何轴对称形状，因而v与θ无关，仅是r、z的函数.

综上，边界条件可写为:

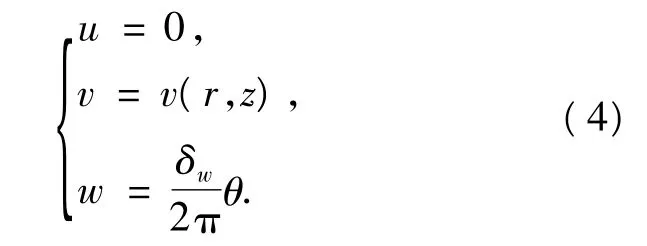
这里，在第1点简化时将周向张缩设为零，即设为没有周向重叠，这主要是为了简化计算，并不完全符合试验结果.但由于该重叠量较小，在剪切应力计算中忽略不会明显影响计算结果.

3.4 求解方程

在圆柱坐标系下，以弹性力学的位移法求解，其几何关系为

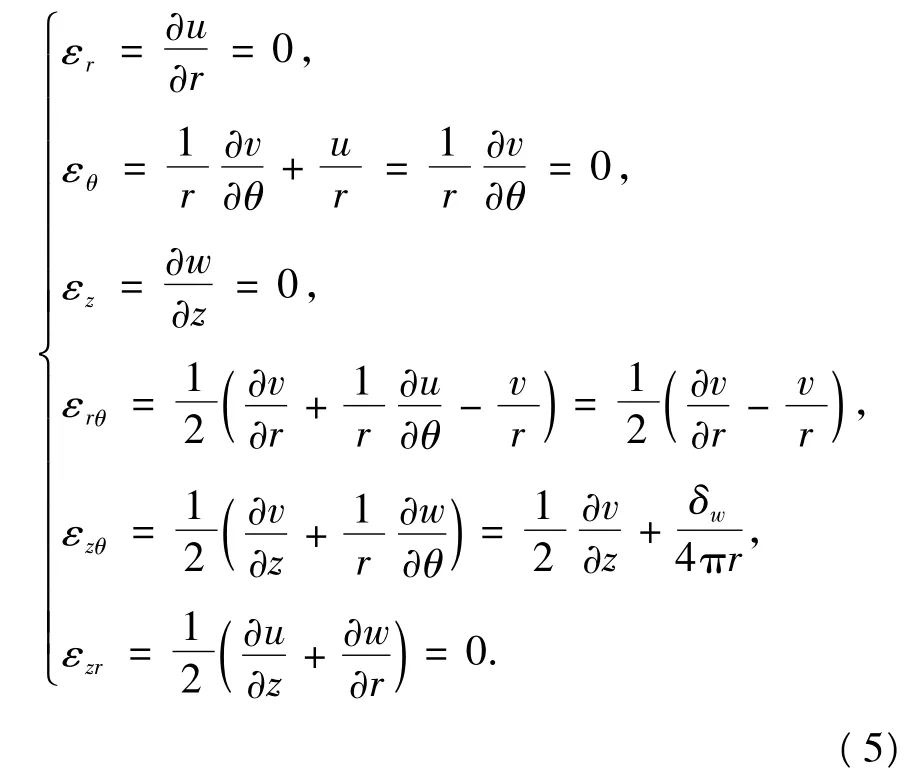
将式(5)代入弹性本构关系式

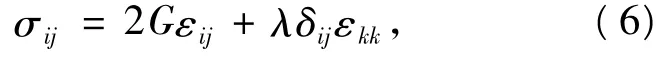
其中

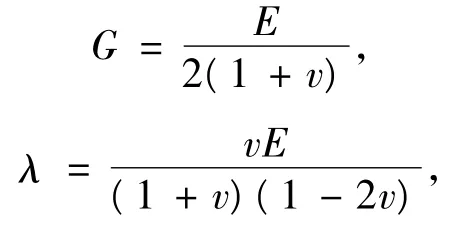
可得到应力表达式为

将式(7)代入式(3)，可得

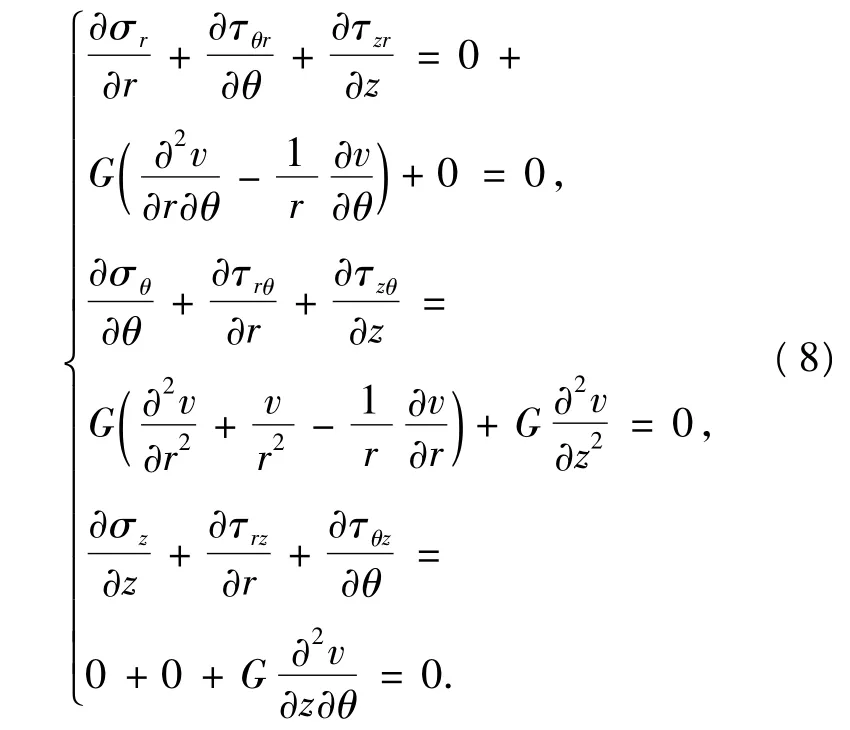
其中C为待定常数.将式(9)回代式(7)，得各应力分量变为

由式可见，除τzθ外其余应力全为零，残余应力为纯剪切状态，符合假设.因在纵向切开前管段处于力平衡状态，则该剪力沿壁厚的合力应为零，即有

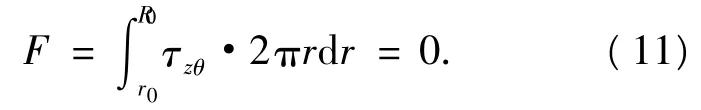
将式(10)代入式(11)中，得

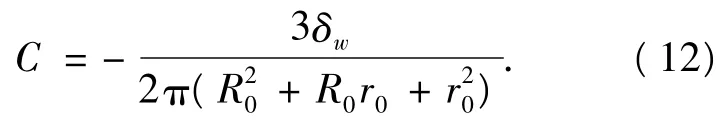
式中，R0，r0分别为管材的外半径和内半径.

将式(12)回代式(9)，得位移v为

相应的应力解，即轴向错开所代表的残余应力分布为

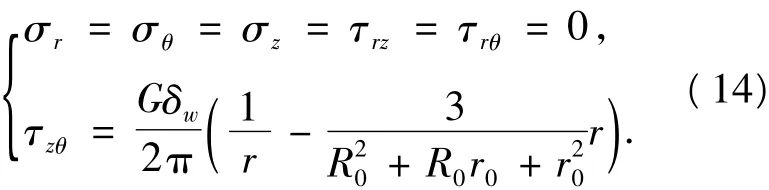
4 结果分析

4.1 解的有效性

由应力式(14)可见，σr，σθ，σz，τrθ，τrz均为零，符合管材内外表面没有应力作用的力边界条件，但剪应力τzθ在上、下端面不为零，这一点与边界上没有外力作用的条件不符.产生不符的原因，是由于采用了简化的位移边界条件.按照板壳理论［13］，对于具有一定宽度的薄壁结构，边界变形影响范围有限.以上分析时不考虑圆环高度的影响，故可以忽略边界情况.同样，根据圣维南原理，这种效应具有局域性，解(14)在环的内部仍然有效.

由式(14)可见，残余剪切应力τzθ与轴向错开量δw成正比，并且沿壁厚分布不同.

4.2 残余剪切应力的分布形式

对式(14)中的半径进行无量纲化处理:

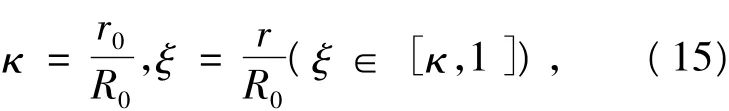
则式(14)变为

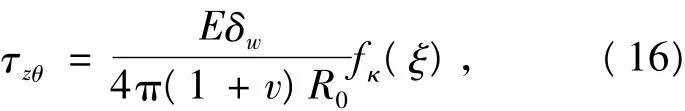
其中

薄壁管材要求外径、壁厚比大于10%，即κ≥0.8.不同薄壁程度(κ值)管材的fκ(ξ)分布如图4所示.

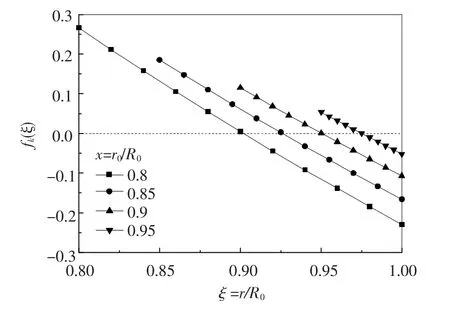
图4 剪切应力函数fk(ξ)的分布

尽管应力函数(17)不是线性函数，但由图4可见，薄壁管的残余剪切应力分布与线性偏离较小.图5是纵切后呈右旋错开管材的残余剪切应力沿壁厚的分布形式.

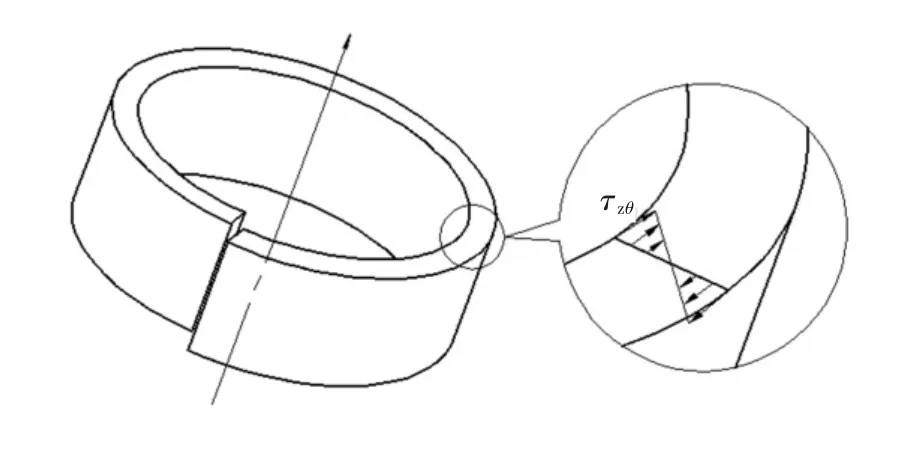
图5 剪应力沿壁厚分布

4.3 残余剪切应力的最大值及样品高度对测量的影响

为确定剪应力最大值及其所在位置，对式(14)求导.计算得τzθ＇(r)＜0，即τzθ(r)为单减函数，因此在r值最小处，即内表面处应力取最大值.该值为

由本式计算试验管材的残余剪切应力，高度依次为20、10和2 mm的样品对应的最大残余剪切应力值依次为33.40、33.52和28.97 MPa.可见高度为20和10 mm两样品的结果非常接近，两者仅相差0.35%.而宽度为2 mm的窄样品的测量结果明显小于前两者，与20 mm高样品的结果差异达13.25%.样品高度对测量结果产生影响，是因为存在端面效应，而窄样品受的端面效应的影响更大.

因此，为较准确地测量旋压管材的残余剪切应力，样品高度不宜过短.

4.4 残余剪切应力产生原因分析

产生残余应力的原因是变形不均.强力旋压时以轴向变形为主，但也存在横向变形.金属横向变形沿壁厚分布不均是造成z－θ残余剪切应力的原因.

管材强力旋压时，管坯安装在芯模上并随其转动，旋轮沿芯模轴向移动.在旋轮压力下，变形区沿管材呈螺旋状运动，逐点将金属加工成所需要的空心回转体制件.受到芯模、旋轮摩擦力的作用，材料沿母线方向出现扭曲，外部扭曲程度大于内部［12］.冷变形最大而且受摩擦条件影响最大的外表面受轴向和周向变形，内层基本是轴向变形［15］.

以正旋为例，旋轮相对于已变形区做螺旋运动，变形区受外载有旋轮正压力和摩擦力，如图6所示.虽然旋压以轴向变形为主，但在扭矩作用下，变形区相对于已变形区有剪切变形，使两道旋纹间存在附加剪切力.受摩擦力与正压力的双重作用，剪切变形和剪切力沿壁厚分布不均，外表面最大，内表面受芯模摩擦作用基本为零.旋压完成卸载后，管材发生扭转，按线性释放部分剪切力，而由于变形不均造成的剪切力保留而成为残余剪切应力.

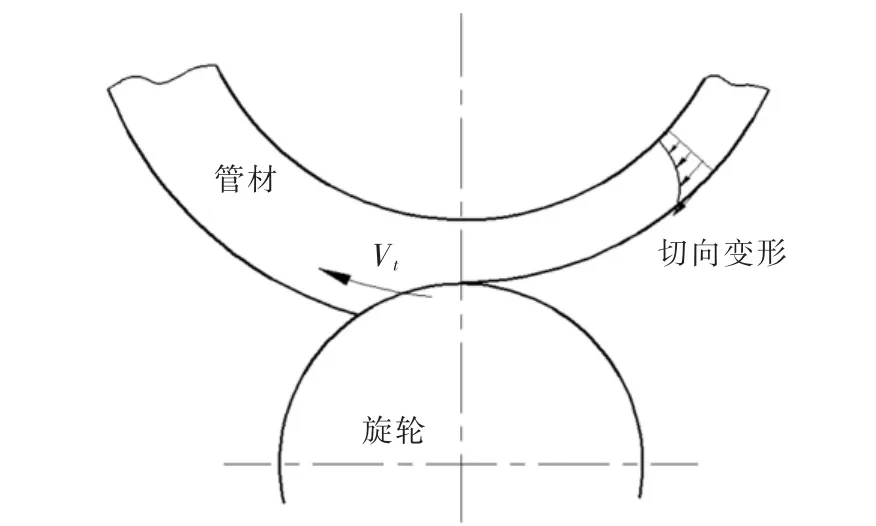
图6 旋压管材周向变形差异

5 结论

强旋薄壁管材沿母线切开一侧管壁后出现纵向错开变形，表明管材存在显著的残余剪切应力.弹性力学分析表明，此变形由z－θ向残余剪切应力释放造成;应力的分布接近线性，具体可由式(14)估算;应力最大值与纵向错开量成正比，所在位置为管材内表面;为较准确地测量旋压管材的残余剪切应力，样品高度不宜过短;管材z－θ向残余剪切应力产生的原因，是旋压时金属横向变形沿壁厚分布不均.

旋压管材的剪切残余应力可用本文建立的方法测量.

［1］ 日本材料学会X线应力测定部门委员会.X射线应力测定法与机械应力测定法的对应关系［J］.材料，1964，135(13):909－914.

［2］ HATFIELD W H，THIRKELL G L.Season cracking［J］.J Inst Met，1919，22:67－126.

［3］ CRAMPTON D K.Internal stress and season cracking in brass tubes［J］.Trans AIME，1930，89:233－255.

［4］ ANDERSON R J，FAHLMAN E G.A method of measuring internal stress in brass tubes［J］.J Inst Met，1924，32:367－383.

［5］ WILLIAM M B J.Residual Stresses in Metals［J］.Amer Soci Test Mat，1949，49:539－582.

［6］ 米谷茂.残余应力的产生和对策［M］.朱荆璞，邵会孟译.北京:机械工业出版社，1983.

［7］ KUBOKI T，NISHIDA K， SAKAKI T，et al.Effect of plug on levelling of residual stress in tube drawing［J］.J Mat Proc Tech，2008，204(1/2/3):162－168.

［8］ 周宜淼，周紫箭.低残余应力管材拉拔配模规程的编制［J］.有色金属加工，2008，37(5):31－34.

［9］ 胡龙飞，刘全坤，王强，等.固定短芯棒拔管残余应力分布规律研究［J］.材料科学与工艺，2008，16 (1):89－93.

［10］ BROWN B F.Stress－corrosion cracking in high strength steels and in titanium and aluminum alloys［M］.Washington D C:NAVAL RESEARCH LABORATORY，1972.

［11］ VAINER E L.Residual stresses in drawn tubes for tubular parts of medical instruments after rolling［J］.Meditsinskaya Tekhnika，1970(1):34－40.

［12］ 申林，陈时先.国外金属旋压发展概况［C］//第一届旋压会议文集.北京:国防工业出版社，1980: 99－108.

［13］ S.铁摩辛柯，S.沃诺斯基.板壳理论［M］.本书翻译组译.北京:科学出版社，1977.

［14］ ASTM:E 1928－07.Standard practice for Estimating the Approximate Residual Circumferential Stress in Straight Thin－walled Tubing［S］，West Conshohocken，Pennsylvania:ASTM International，2007.

［15］ 葛文翰.对强力旋压的燃烧室表面残余应力的初步分析［C］//第二届旋压会议文集.北京:兵器工业部，1984:1－11.

Measuring method of z-θ directional residual shear stress in spun thin-walled tube

ZHANG Zhen，SU Guo-yue
(Institute of Metal Research，China Academy of Sciences，Shenyang 110086，China，E-mail:zzhang@imr.ac.cn)

In order to establish measuring method of residual shear stress in spun thin-walled tube，and estimate the residual stress in spun 2024Al sample tube，sample tubes are subjected to one side split and the deformation are measured.On the basis of deformation simplification，the residual shear stress fomula are derived through elastic mechanics deduction，and the residual stress of sample tubes are calculated.The results show that the prominent z－θ directional residual shear stress exists in sample tubes，and its value is direct proportional to the axial stagger of sides along the generatrix，the residual shear stress distribution is nearly linear along wall thickness，and the max value lies on the inner surface of the tube.The method established in this paper can be used to measrue the z－θ directional residual shear stress in spun thin-walled tubes.

spin;tube;residual shear stress

TG302 文献标志码：A 文章编号：1005－0299(2011)05－0111－05

2010－11－30.

张 振(1975－)，男，博士，助理研究员;

苏国跃(1960－)，男，研究员.

(编辑 程利冬)