质量成本模糊神经控制模型的建立研究

尚珊珊,尤建新

(同济大学 经济与管理学院,上海 200092)

●模型研究

质量成本模糊神经控制模型的建立研究

尚珊珊,尤建新

(同济大学 经济与管理学院,上海 200092)

文章在 PAF(预防成本、鉴定成本和损失成本)模型思想的基础上,根据分析影响质量成本的主要因素及其控制方法,建立较为智能实用的质量成本模糊神经控制器。首先根据各种研究文献以及实际情况设置较为通用的质量成本三级科目。然后根据历史数据对各科目做 Pareto分析,找出影响质量成本的主要影响科目,利用统计分析中的相关分析以及偏相关分析降维,找出真正影响质量成本的主要科目。而后,根据分析主要影响科目及造成科目成本的主要影响因素,利用模糊控制方法以及神经网络建立质量成本控制模型,并详细讨论了模糊神经控制器的输入、输出集的语言值及模糊隶属度、控制器的模糊规则、神经网络隐层数的确定、隐层神经元数目的确定以及其网络学习规则。

质量成本控制模型;模糊控制;神经网络;PAF模型;Pareto分析

一、引 言

学者对质量成本模型的讨论主要有四类主要模型:P-A-F模型[1]或 Crosby模型[2]、机会成本模型[3]、过程成本模型[4]或 ABC模型[5]。大多数 CoQ模型是基于 P-A-F模型分类的基础之上的。Feigenbaum质量成本模型提出预防和鉴定成本随着质量水平的提升而增加,损失成本随着质量水平的提升而降低,而且鉴定成本、损失成本两者可以达到一个最佳平衡点 c,在该平衡点 c处质量成本总额达到最低[6,7]。Juran质量成本模型提出了质量成本水平分为三个区域,即质量改进区、质量适宜区以及质量过剩区[8,9]。他们的质量成本模型为以后质量成本的更深入研究奠定了基础,以后陆续有学者研究质量成本的科目设置[10]、质量成本最低的最佳模型[11,17-19]。对于质量成本的控制研究一般较少且较为浅显,主要集中于针对每个质量成本科目所发生成本的一般概念性控制,本文则将模糊控制方法与神经网络应用到质量成本控制过程中,并据此建立了质量成本控制模型,讨论了质量成本模糊神经控制的隐层数的确定、隐层神经元数目的确定以及网络学习规则。

二、质量成本的科目设置

本文采用 PAF的质量成本模型,即总质量成本 (CoQ)=预防成本 (P) +鉴定成本 (A) +内部损失成本 (IF)+外部损失成本 (OF),根据各文献中有关质量成本科目的设置及实际情况,设置质量成本三级科目[13-16],设置情况如表 1所示。

三、质量成本的主要影响因素分析

首先对各三级科目进行数据收集与分析,找出科目间的相关性,然后作出 Pareto图,找出其中主要影响质量成本额的科目。

表1 质量成本科目表

(一)主要影响科目分析

1.Pareto分析

根据企业历史数据,可以统一格式化数据到质量成本数据统计表中,设共有 n组历史数据,根据数据表对设占总成本前 80%的科目进行排序分析,用 C1～C6表示前 6位科目,所以 {C1～C6}∈ {P1,P2,P3…,OF4},根据表可以做出帕累托图,如图 1所示。因此,可以分析得出主要影响科目为 C1～C6。

2.相关性分析

从 pareto分析中可以看出,17个科目中,占质量成本比例90%只有6个科目,可以对这六个科目再次做相关性分析,计算得出相关系数矩阵:

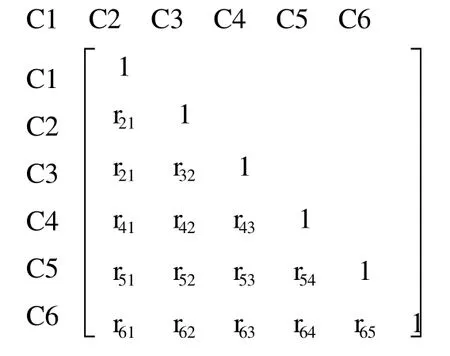
对于两科目间相关系数 rij>0.7的值说明两科目间具有较强相关性,因此,找出并分析相关系数 rij>0.7的科目。

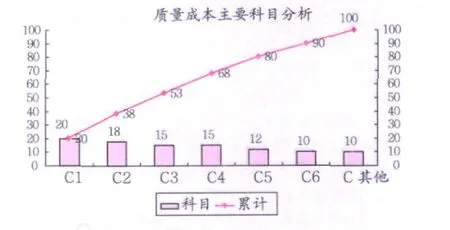
图1 质量成本主要影响科目 Pareto分析图 (单位:%)

3.偏相关分析

由于简单的相关分析仅仅是分析两个变量间的线性关系,往往会因为第三个变量的作用,使得相关系数不能准确的反映两个变量间的线性程度[12]。因此,首先需计算得出偏相关系数值,然后利用假设检验,检验偏相关系数[20]。从相关矩阵中,可以看出各科目间的相关关系,找出与科目Ci具有强相关性的所有科目 Cj,Ck,…,Cl,然后依次做偏相关分析,即依次计算各偏相关系数,即计算 rij,k,rik,l,…,rik,l,ril,j,ril,k,如假设 C1与 C2,C3,C4具有强相关性,求偏相关系数,如表 2所示,通过计算偏相关系数及检验,可以分析得出真正具有相关性的相关科目。然后可以达到进一步降维分析的目的。

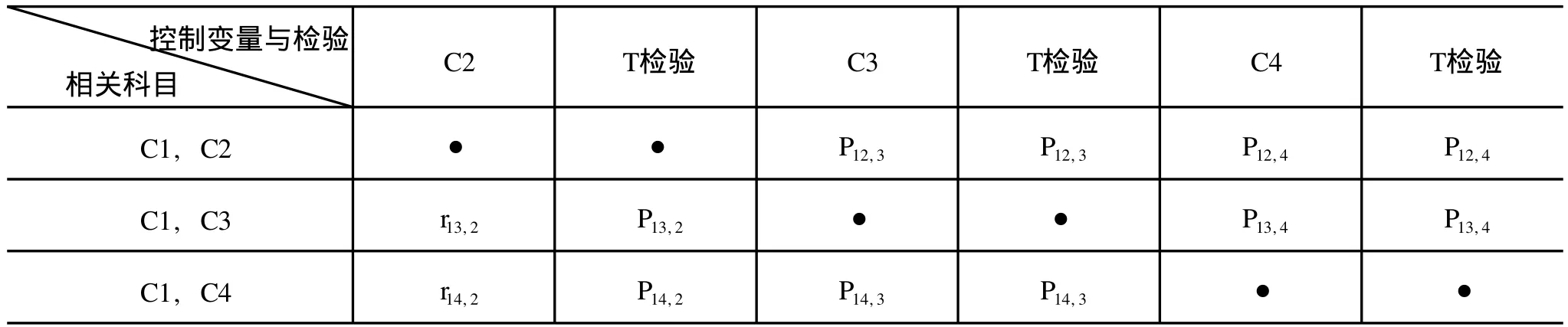
表2 偏相关系数与检验

(二)主要影响因素分析

在影响质量成本总额的主要影响科目中,分析造成这些科目所对应的质量成本较高的原因,而产生原因中有些是可控因素,即可以人为的通过改变某种方式或转换某种渠道而达到降低成本的目的,但是有些因素是不可控因素,这些因素所造成的成本则是不可避免的。质量成本产生的原因为原材料质量不合格、生产过程中的问题如设备问题抽检所造成的在制品或成品质量不合格,因此影响质量成本的主要因素有原材料合格率、过程产品抽检合格率、产品成品合格率以及设备故障率,根据前面分析得出的主要影响科目从而判断各主要影响因素的高低。

四、模糊神经网络质量成本控制器的建立

一般的模糊控制是将 “专家经验”通过模糊控制规则表现出来,运行中通过查表做出控制决策,这样虽然比设定程序更先进,但是会造成占用大量的内存空间,查表反映速度慢,只是按照已经编入的规则进行控制,因此不够理想[21-22]。所以,可以引入神经网络,将神经网络与模糊控制相结合,利用离线训练好的网络,通过在线计算即可得到最佳输出。这种控制模式反应速度快,而且神经网络又具有自学习功能和联想能力,对于未来在训练中出现的样本,也可以通过联想记忆的功能,做出决策,表现也会比较灵活。模糊神经控制器与一般的模糊控制器类似,只是学习规则中引用了神经网络。

根据质量成本原理,一般开始阶段,质量损失成本与预防和鉴定成本可以达到一个较好的平衡点,加强预防和鉴定成本可以降低损失成本,从而开始阶段有利于降低总质量成本。

(一)模糊子集的定义

输入子集的定义:

原材料抽检合格率MPR:{很低,低,中,高,很高}

产品抽检合格率 PR:{很低,低,中,高,很高}

设备无故障率W:{很低,低,中,高,很高}

其中合格率为[0,1]间的数字,0表示最低,1表最高。

设模糊子集的语言值为:{NB,NS,ZO,PS,PB}

合格率隶属度模糊子集的定义如图 2所示。设很低 =NB(x),低 =NS(x),中 =ZO(x),高 =PS(x),很高 =PB(x),其中,x表示合格率。

其隶属度表达式为:

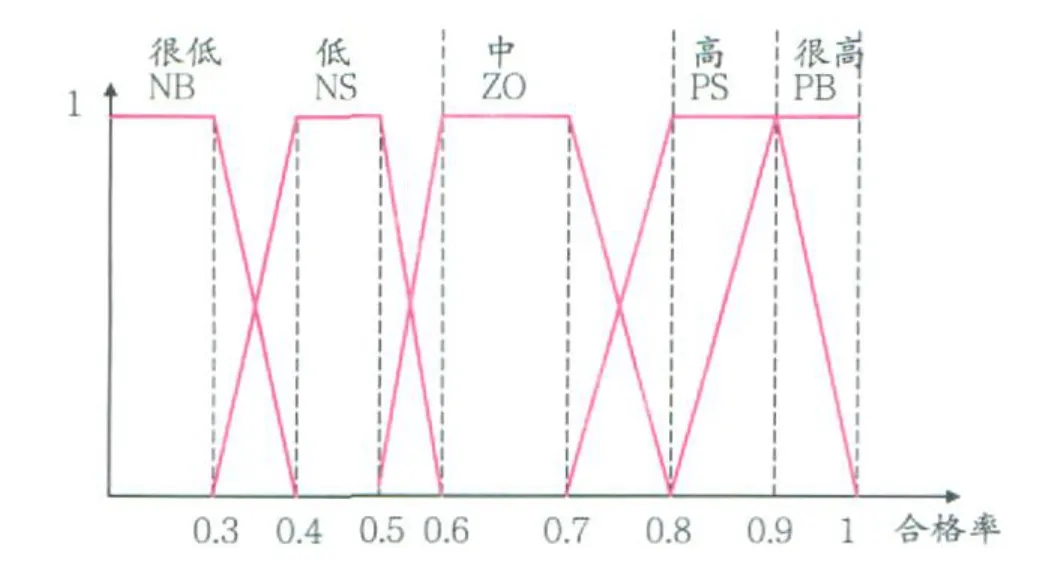
图2 输入模糊子集定义

输出子集定义:

检测与控制力度 PAC: {大幅降低,降低,中,加强,大幅加强}

检测与控制力度的论域为 Y,划分为七个等级,模糊子集的语言值为:{NB,NS,ZO,PS,PB},模糊隶属度的定义如图 3所示。设低 =NB(y),较低 =NS(y),中 =ZO(y),高=PS(y),较高 =PB(y),其中,y检测与控制力度。

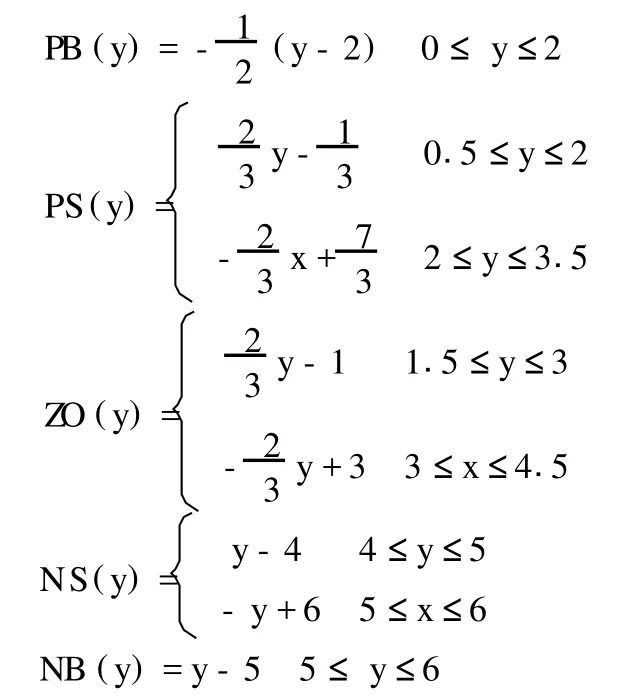
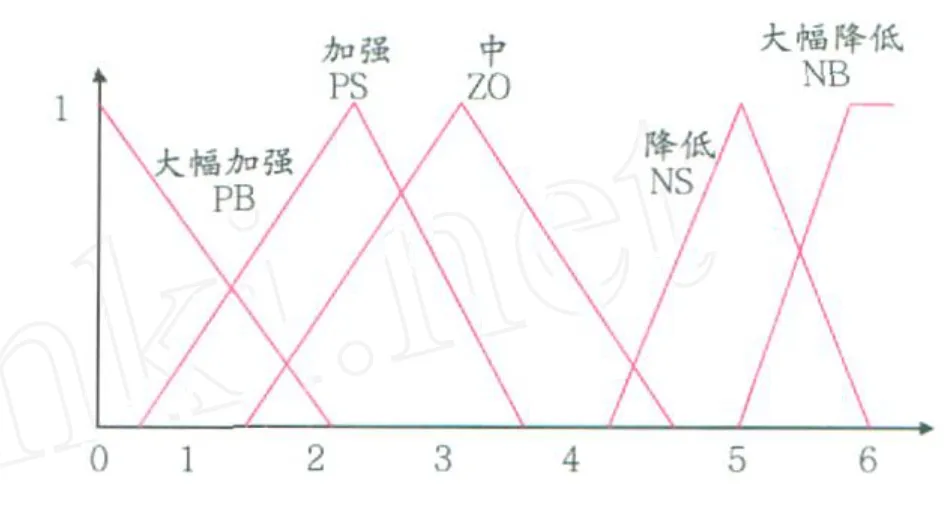
图3 输出模糊子集定义

(二)模糊规则的确定

令原材料抽检合格率 MPR为{x1,x2,x3,x4,x5},产品抽检合格率 PR为{x6,x7,x8,x9,x10},设备无故障率 W为{x11,x12,x13,x14,x15},表示 {很低 ,低 ,中 ,高 ,很高 },对应的语言数值为{NB,NS,ZO,PS,PB};检测与控制力度 PAC为{y1,y2,y3,y4,y5},表示 {大幅降低,降低,中,加强,大幅加强},其对应的语言值为{NB,NS,ZO,PS,PB}。制定模糊规则如表 3、表 4、表 5、表 6、表 7所列。

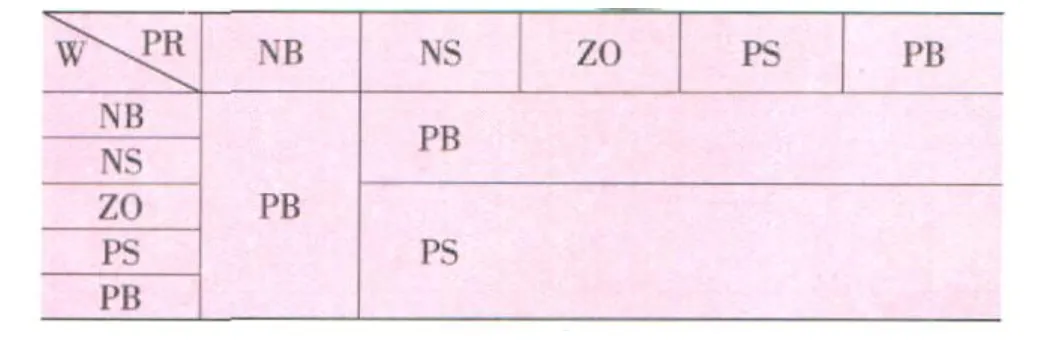
表3 MPR=NB时的模糊规则

表4 MPR=NS时的模糊规则

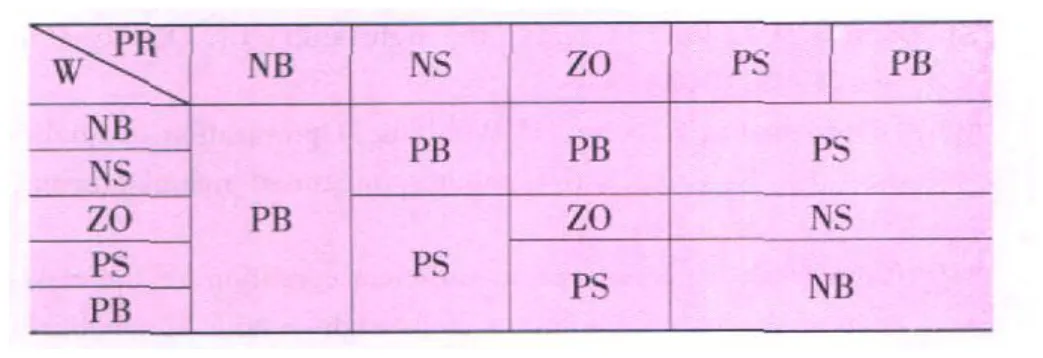
表5 MPR=ZO时的模糊规则

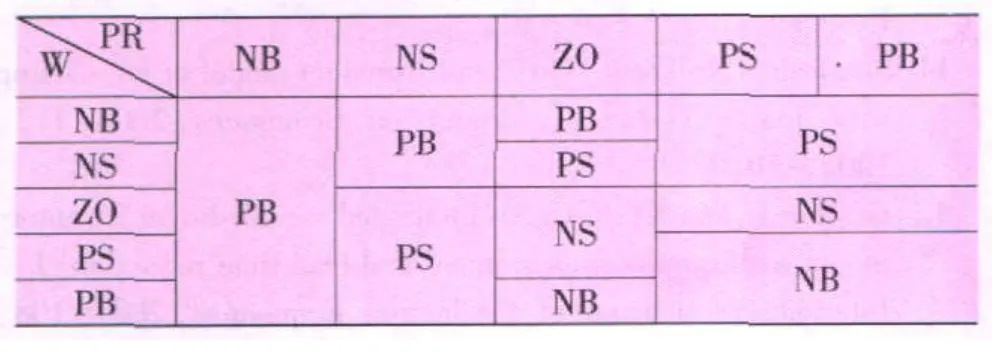
表6 MPR=PS时的模糊规则

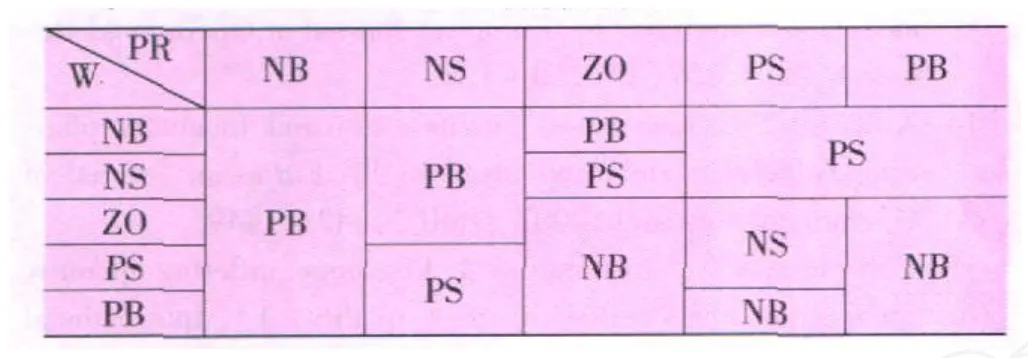
表7 MPR=PB时的模糊规则

(三)模糊神经网络控制器的建立

令原材料抽检合格率MPR为{x1,x2,x3,x4,x5},产品抽检合格率 PR为{x6,x7,x8,x9,x10},设备无故障率 W为{x11,x12,x13,x14,x15},检测与控制力度 PAC为{y1,y2,y3,y4,y5},其神经网络结构图如图 4所示,模糊神经网络控制器如图 5所示。因此,根据神经网模糊络控制器,可以根据归结出来的少数几个变量,得出质量控制结论。文章采用 BP神经网络。

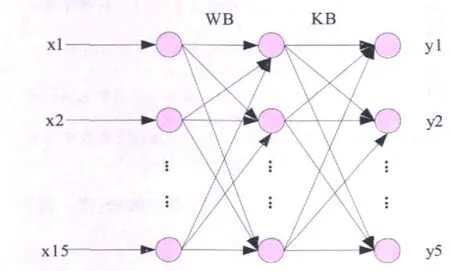
图4 神经网络结构图

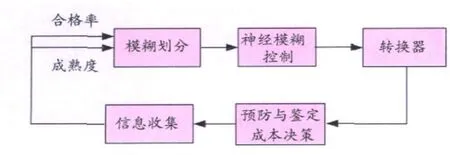
图5 神经模糊控制器

隐层数的确定:BP网络属于前馈网络。它可看成是一从输入到输出的高度非线性映射。Hecht-Nielsen于 1987年证明了 Kolmogorov定理[23]。其内容为::给定任何一个连续函数 f:Un→Rm,Y=f(X),其中,Un∈0,1,f可以精确地用一个三层前馈网络实现,该网络的第一层 (即输入层)有 n个神经元,中间隐含层有 2n+1个神经元,第三层 (即输出层)有 m个神经元。ko lmogorov定理表明含一个隐层的BP前馈网络是一种通用的函数逼近器,为逼近一个连续函数,一个隐层是足够的。当要学习不连续函数时,则需要两个隐层,即隐层数最多两层即可。由于输入元素个数为 15,输入数量并不庞大,我们采用一个隐层。

隐层神经元数目的确定:选择隐层神经元数是很重要的问题。隐层神经元个数太少,则网络所能获取的用以解决问题的信息太少;个数太多,不仅增加训练的时间,难以在人们能够接受的时间内完成训练,更重要的是过多的隐节点,还可能引起所谓的“过度吻合”(over-fitting)问题。值得注意的是,增加隐层结点可以减少训练误差,但超过某一隐结点数后,测试误差反而增大,即泛化能力下降。训练误差小并不意味着网络的泛化能力就强。因此,这里仍采用经验公式 n1=log2n来确定隐层神经元的数目,其中 n为输入单元数,n1为隐含层神经元数。

网络学习规则:网络输入向量 Pk=(x1,x2,…,x15);网络目标向量 Tk=(y1,y2,y3,y4,y5);中间层单元输入向量 Sk=(s1,s2,s3,s4),输出向量 Bk=(b1,b2,b3,b4);输出层单元输入向量为 Lk=(l1,l2,l3,l4),输出向量为 Ck=(c1,c2,c3,c4);输入层只至中间层的连接权wij,i=1,2,3,…,16,j=1,2,3,4;中间层至输出层的连接权 vij,i=1,2,3,4,j=1,2,3,4;中间层各单元的输出阀值θj,j=1,2,3,4;输出层各单元的输出阀值γj,j=1,2,3,4;参数 k=1,2,…,m。

(1)初始化。给每个连接权值 wij、vij阀值θj与γj赋予区间 (-1,1)内的随机值;

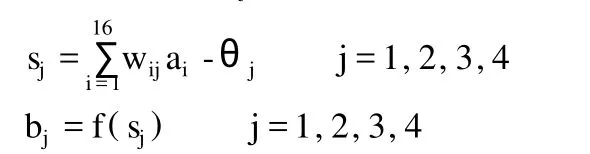
(4)利用中间层的输出 bj、连接权 vij和阀值γj技术输出层各单元的输出 Lt,然后通过传递函数计算输出层各单元的响应Ct:

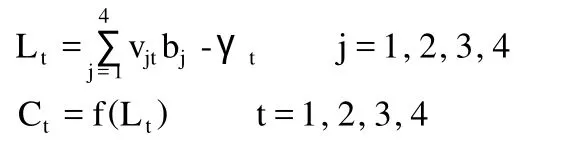
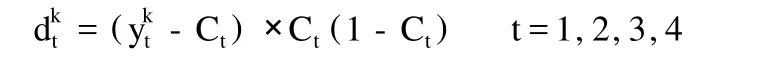
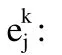
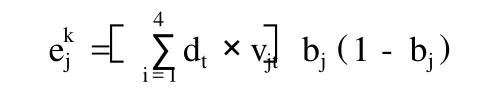
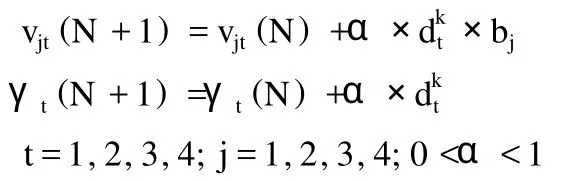
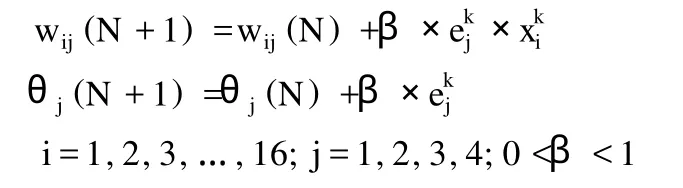
(9)随即选取下一个学习样本向量提供给网络,返回到步骤 (3),直到m个训练样本训练完毕;

(10)重新从m个学习样本中随即选取一组输入和目标样本,返回步骤 (3),直到网络全局误差 E小于预先设定的一个极小值,即网络收敛。

五、结 论

如今越来越多的企业关注质量成本,但是以往文献对质量成本大都是概念上或理论上的研究,从而使其在实际运用中存在一定的障碍。本文在深入研究以往文献的基础上设置符合实际的较为通用的质量成本三级科目。深入讨论了在对三级科目进行 pareto分析、相关分析后,发现影响质量成本的主要科目及在主要影响科目的分析基础上对找出主要原因,而后文章根据模糊控制系统以及神经网络的方法建立质量成本模糊神经控制器,讨论了该控制器的隐层数、隐层神经元数以及网络的学习规则,从而为企业的质量成本控制及控制自动化方面具有理论以及实际指导意义。

[1]Baatz EB.What is return on quality,andwhy you should care[J].Electronic News,1992,10:60.

[2]Bemowski K.The benchmarking bandwagon[J].Quality Progress,1991,24:8.

[3]Bohan G P,Horney F N.Pinpointing the real cost of quality in a service company[J].National Productivity Review,1991,10(3):309.

[4]Burgess T F.Modeling quality-cost dynamics[J].International Journal ofQuality&ReliabilityManagement,1997,13(3):8.

[5]Baatz E B.What is return on quality,and why you should care?[J].Electronic News,1992,10:60-62.

[6]Bemowski K.The benchmarking bandwagon[J].Quality Progress,1991,24:20-23.

[7]Bohan G P,Horney F N.Pinpointing the real cost of quality in a service company[J].National Productivity Review,1997,10(3):309-311.

[8]Bottorff D L.CoQ systems:the right stuff[J].Quality Progress,1997,10(3):33-35.

[9]M Opper mann,W Sauer,H Wohlrabe.Optimization of quality costs[J].Robotics and Computer integrated manufacturing,2004,19:135-140.

[10]Chung K J.A necessary and sufficient condition for the existence of the optimal solution of a single-vendor single buyer integrated production-inventory model with process unreliability consideration[J].International Journal of Production Economics,2007,8:6-10.

[11]Shailesh S Kulkarni.On amulti-productmodelof lot-sizing with quality costs[J].Production Economics,2008,112:1002-1010.

[12]OuyangL,Wu K,Ho C.An integrated vendor-buyer inventory modelwith quality improvement and lead time reduction[J].International Journal of Production Economics,2007,108:349-358.

[13]Kulkarni S,Prybutok.Process inves tment and loss functions:models and analysis[J].European JournalofOperationalResearch,2004,157(1):120-129.

[14]Kulkarni S S.Loss-based quality costs and inventory planning:General models and insights[J].European Journal of Operational Research,2007,188(2):428-449.

[15]Papachristos S,Konstantaras I.Economic ordering quantity models for items with imperfect quality[J].International Journal of Production Economics,2006,100:148-154.

[16]Rezaei J,Davoodi M.A deter ministic,multi-item inventory modelwith supplier selection and imperfect quality[J].AppliedMathematicalModeling,2007,7:9-15.

[17]梁淑明,张根保.质量成本与西格玛能力之关系模型探讨[J].管理技术,2006,(5):103-105.

[18]王华.最佳质量成本决策方法 [J].商业经济,2004,(5):51-55.

[19]刘东才,雒征,张文华.最佳质量成本模型的研究 [J].武汉理工大学学报,2007,(5):160-164.

[20]白宝光,张世英.质量成本模型及其优 [J].科学管理研究,2005,23:20-33.

[21]汪邦军.质量成本曲线方程与质量改进的经济分析[J].北京机械学院学报,2002,(2):65-70.

[22]马少辉,刘金兰.Pareto/NBD模型实证与应用研究[J].管理科学,2006,19(5):45-49.

[23]刘子先,门峰.动态竞争环境下的产品保证管理最优控制策略研究[J].管理科学,2009,22(3):2-8.

The Research on the Establishment of Fuzzy NeuralM odel

SHANG Shan-shan,YOU Jian-xin
(School of Econom ics and M anagement,TongjiUniversity,Shanghai200092,China)

Based on the PAF(prevention cost,appraisal cost and failure cost)model,according to the analysis on the main influential factors and its controlmethod,this paper establishes a more intelligent fuzzy neural quality controller.First of all,it sets the three level subjects by through research on the dissertations.Then it does Pareto analysiswith the historic data,finding the main influential subjects on the quality cost,by taking use of the correlation analysis and partial correlation analysis to reduce the dimension so that to find the actual influential subjects.Finally,the paper establishes the quality cost controller based on the fuzzy controlmethod and the neural network theory,and discusses the linguistic value and the fuzzymembership degree of the input and the output fuzzy subsets in detail,and it sets the fuzzy rulesof the controller,and talks about the determination of the numberof the hidden layer,the numberof the neurons in the hidden layer,and their study rules.

quality cost controlmodel;fuzzy control;neural network;PAF model;Pareto analysis

F270.5

A

1007—5097(2011)01—0142—05

10.3969/j.issn.1007-5097.2011.01.034

2009—10—23

国家自然科学基金“服务运作管理理论、方法和关键技术研究”(70832005)

尚珊珊 (1983—),女,河南安阳人,博士研究生,研究方向:管理理论与工业工程;

尤建新 (1961—),男,江苏苏州人,院长,教授,博士,研究方向:管理理论与工业工程。

[责任编辑:张 青 ]