B-S模型在中国权证定价中的应用

耿照源，金佩文

（浙江大学 城市学院商学院，杭州 310015）

B-S模型在中国权证定价中的应用

耿照源，金佩文

（浙江大学 城市学院商学院，杭州 310015）

文章构建了修正的B-S模型，为我国权证进行了理论定价，并考察了权证市场价格与理论价格之间的偏差。为了克服经典B-S模型自带假设对定价准确性的限制，使用调整后EMA模型对标的证券历史波动率的计量进行了改进并运用格点搜索法确定了最佳衰减因子，同时比较了EMA模型与调整后EMA模型在对历史波动率进行估算时的有效性。

权证定价；备兑权证；B-S模型；EMA模型；格点搜索法

0 引言

权证的定价在国外很早就有研究，形成了比较完善的定价理论系统和以B-S模型为主体的有效计量方法体系[1]。国内的研究尚处于发展阶段，现有的资料主要集中在对B-S模型在我国权证市场定价的适用性讨论上，缺乏对B-S模型自带假设限制进行修正使之更为精确的研究。笔者以此为突破口，创造性地提出调整后EMA模型计量标的资产波动率，修正了B-S模型关于常数波动率的假设，并得到上述更适合我国备兑权证定价的模型。

配合2011年政策重推备兑权证的历史背景，本文选备兑权证为数据来源，通过实证得到更合理的备兑权证定价模型，为我国权证市场的正确定价和健康发展提供了建设性参考。

1 问题的提出

我国权证市场于2005年8月，因股改等因素，在沉睡19年后重新开启权证交易，不到一年就跃居全球第二大权证交易市场。这种发展潜力决定了对我国权证产品进行合理定价是颇具现实意义的。

但同时，我国权证市场存在两大重要缺陷。其一是市场投机泡沫过剩和产品定价不合理。为了保证权证市场的健康发展，限制投机泡沫，就有必要反思权证的定价，这也正是本文研究的出发点。其二是产品数量的稀少和产品种类的单一。自2005年恢复交易以来，我国上市权证从未超过40支，其中备兑权证平均占比不到25%。区别于股本权证，备兑权证流动性更好，期限相对更短[2]。其交易量在全球占权证总交易量的95%以上。而我国也拟在2011年3月重新推出备兑权证交易制度，重振权证市场。基于以上原因，笔者选取备兑权证的定价作为本次研究的研究对象。

2 模型的建立

本文主要构建的是备兑权证的定价模型。此定价模型由B-S模型原型修正得来。

B-S模型公式如下所示：

其中，

C(S，T)：购买一份欧式看涨期权的价值；

S：标的资产现价；

T：认股权证的到期时间；

K：期权的执行价格；

r：在T时刻到期的投资的无风险利率；

σ：标的资产价格的年波动率；

N(x)表示标准正态分布变量的累计概率分布函数[3]。

本文定价对象是我国备兑权证，它可视作典型的欧式看涨期权，所以使用B-S模型对其进行定价是合理的。但B-S模型自带的关于金融市场、标的资产和期权特征的苛刻的约束不同程度制约了其定价的准确性[4]。以故本文将对其进行修正。

在衍生品定价中，除行为金融理论外，几乎所有定价模型都包括完美市场假设，所以基于金融市场条件假设的改进是不现实的。

唯一必要且可行的修正落在标的资产假设条件上。大量实证研究表明股利提前支付假设产生的偏差并不显著；而备兑权证本身又不产生股权稀释效应，从而排除了对股权稀释效应的修正。本文最终选取常数波动率假设作为突破口对B-S模型进行改进。

为修正B-S模型的常数波动率假设，本文创造性地使用调整后EMA模型来计量标的股票的收益波动率。EMA（Ex-ponentially Moving Average）模型，即指数加权移动平均模型。所谓指数加权移动平均，是一种动态统计量，其预测值实质上是以前观测值的加权和，并对越久的历史数据给予越低的权重[5]。EMA模型理论原型假设标的资产收益率服从正态分布，即 Rt～N(0,σ2)，计算公式如下：

其中，

σt：t日的波动率；

λ：衰减因子（0＜λ＜1）；

μ：样本期间的平均收益率；

Rt-1：t-1 日的收益率[6]。

SIAH连续信息到达假说认为，波动率与成交量存在正向的相关关系。基于此假说，何蓉于2009年对EMA模型进行了相关调整，公式如下：

其中，

γ为常数系数；

VL为权证收益率的长期波动率。

基于以上两大理论模型，笔者推导出本文使用的修正后B-S模型，使用调整后EMA模型对σt进行计量，并设定n=60，即以样本期起始之日之前60个交易日的标准差作为初始波动率σ0，由此得到最终B-S模型使用的σ。

3 基于中国权证数据的实证分析

3.1 数据的选取

本文实证采用的是时间序列数据，主要包括鞍钢JTC1、五粮YGC1、雅戈QCB1三支认购备兑权证从开市到退市的价格数据和相应的标的股票价格数据。

除权证和标的资产价格外，B-S模型还要求同期的无风险利率。本文使用7天期国债回购利率来替代无风险利率，数据列表详见附录A。

3.2 实证检验

3.2.1 衰减因子λ的确定

为确定最佳衰减因子值，本文使用格点搜索法，将λ取值为0.1、0.5、0.8和0.95分别进行试算。根据定义，最佳衰减因子需使得理论价格与市场价格的累积偏差最小，也即实现，其中Pi为市场价格，Ci为理论价格。结果汇总见表1：λ应取值0.95。

3.2.2 EMA模型调整效果检验

为验证调整后EMA模型的有效性，本文比较了三支标的股票收益波动率分别在调整后EMA模型和原始EMA模型计量下的累积偏差。汇总结果可参照表1和表2。

结果显示，在所有四支权证的估价中，用调整后EMA模型计量的标的股票收益波动率形成的价格累计偏差均比EMA模型计量标的股票收益波动率形成的价格累计偏差小。可见，调整后EMA模型达到了预期的效果，这也保证了本文对B-S模型修正的有效性。

表1 调整后EMA模型的累计价格偏差表

表2 原始EMA模型的累计价格偏差表

3.2.3 修正后B-S模型估价的有理性检验

在有理性检验部分，本文将三支认购备兑权证及其标的股票价格的信息导入修正后的B-S模型得到各支权证的BS模型理论价格。为确保实证的完整性，笔者在估价过程中保留了四只权证分别从开市到退市所有交易日数据。

此部分的重点是定量检验修正后B-S模型在我国备兑权证市场应用的有效性。图1-3直观地展现了三支权证市场价格和B-S模型理论价格的偏差及拟合情况：

为验证定价的有效性，本文计算了在全样本期间内各权证的市场价格与B-S模型理论价格之间的偏差，并设定合理偏差范围为±5%。具体计算方法为：Dif=(Pi-Ci)/Ci，其中Dif为偏差，Pi为市场价格，Ci为理论价格。统计结果见表3。

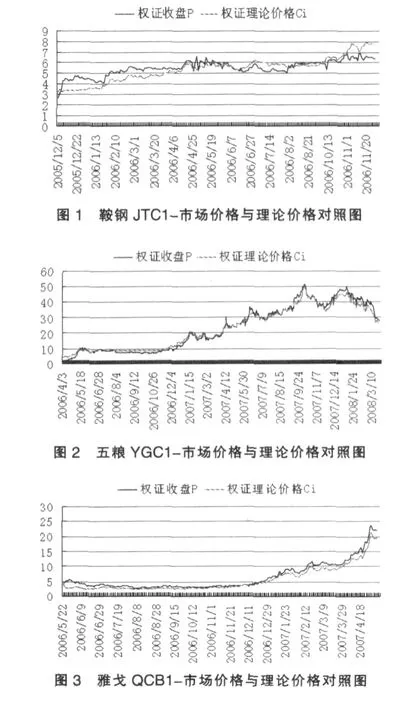
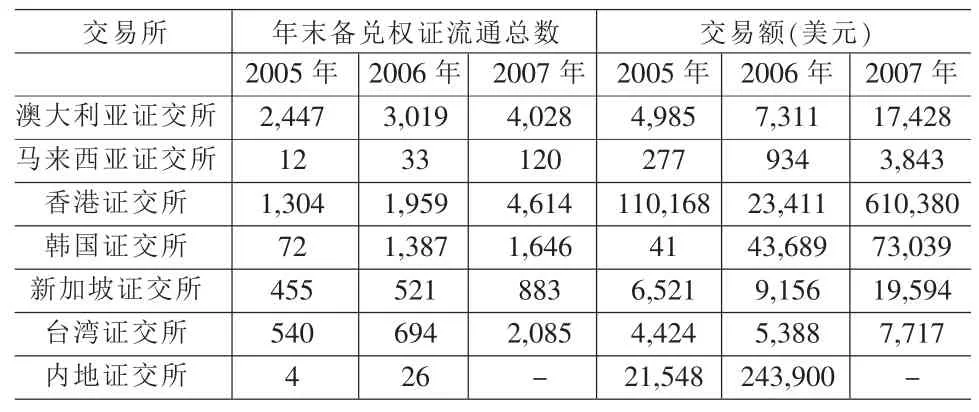
表4 世界主要权证市场交易信息汇总表

结果显示，三支权证价格的总体偏差除“雅戈QCB1”外均在±5%以内，表明市场价格接近理论价格。样本整体的平均偏差度为7.24%。当然，“雅戈QCB1”超过20%的偏差度是不容忽视的，其正数的大幅度偏差表明它的市场价值明显高于B-S模型理论价值。

3.2.4 实证结果的解释

从以上实证结果来看，我国备兑权证的市场定价和基于修正后B-S模型的理论价格之间存在部分差异，并且表现为市场价格高于理论价格。笔者认为，权证市场的流动性过剩和过度投机是权证价格被高估的重要原因。

本文将国内权证市场分别与国内股票市场和国外权证市场做了比较，发现我国权证市场的流动性明显过高。以表4中2006年的数据为例，拥有最少发行数量的内地权证市场创造了所有交易所中最大的权证交易额。这种过高的流动性很可能是权证产品被市场高估的重要原因，而肖钢在2007年的研究也证实了权证及其标的股票的规模和流动性会对权证的定价产生显著影响。

作为我国权证市场罕有的金融衍生工具之一，随着股改风潮而开启的权证受到了投资者的广泛关注。除理性因素外，投资者的“羊群效应”也可以解释高估现象。在国内，小额个人投资者占了权证投资者的大部分。他们有限的金融知识使其简单地将未来大盘涨跌预期视作影响权证价格的主要因素，而本次研究的2005～2008年适逢国内股票市场的大牛市，市场对未来的预期普遍乐观。这种乐观预期带来的认购权证热也就导致了本次研究中的部分权证被高估。

4 结论

本文基于权证定价的B-S模型和计量资产波动率的调整后EMA模型构建了备兑权证定价的修正的B-S模型。通过整个实证过程可见，用调整的EMA模型对标的资产的市场价格波动率的估计获得了良好的效果。但基于修正的B-S模型对中国备兑权证计量得到的理论价格和实际市场价格的偏离仍然存在，不过此类情况可以由市场结构、特定时期的乐观预期所解释。多数权证的有效定价使得修正后B-S模型仍不失为国内备兑权证定价的优化方案。

本文认为有以下两方面值得继续研究的问题：一是权证存续期内不同时期定价偏差的比较，二是市场流动性对权证价格的影响。相信此类研究会令到我国权证定价的体系更为完善。

[1]杨国梁.财务经济学[M].台北：五南图书出版股份有限公司，2004.

[2]孙妩.我国推出备兑权证的可行性分析[J].现代商业，2010,(15).

[3]Black F,Scholes M.The Pricing of Options and Corporate Liabilities[J].Journal of Political Economy,1973,(81).

[4]葨谷千鳳彥.細說 Black-Scholes 模型[M].台北：鼎茂出版社，2005.

[5]白双梅，杜福洲.基于马尔可夫链的EWMA控制图参数优化及其实现[J].制造业自动化，2010,(6).

[6]王海宇，徐济超，杨剑锋，常广庶.基于APL的EWMA图优化设计[J].系统工程理论方法应用，2006，15(1).

F224

A

1002－6487（2011）11－0146-03

（责任编辑/亦 民）