基于演化博弈的排污权交易市场均衡分析

艾江鸿

（重庆大学 经济与工商管理学院，重庆 400044）

基于演化博弈的排污权交易市场均衡分析

艾江鸿

（重庆大学 经济与工商管理学院，重庆 400044）

文章基于非对称演化博弈原理，分别对一级与二级密封拍卖下的排污权交易市场演化情况进行分析，在此基础上，从市场效率的角度对上述演化均衡进行政策分析，分析结果表明：在两种不同的拍卖机制下，通过选择适当的竞价下限，可诱导排污企业选择竞价上限作为其最优选择，从而带来高的市场效率。

演化博弈；排污权交易；拍卖机制；市场均衡

0 引言

排污权交易作为重要的环境政策手段，得到了国内外经济学者的关注。并且有多项国家自然科学基金对该方向研究进行了资助，并取得了一批具有理论价值和现实意思的研究成果，为我国排污权市场的建立和发展提供了理论依据和政策建议。

在交易成本假设下，初始排污权分配对实现总量控制目标和深化排污权交易制度非常关键。现有文献多针对免费分配方式（如：李寿德 黄桐城，2004，2006；赵海霞，2006；赵文会，2008）。但是，免费分配方式会导致效益损失和妨碍竞争[1],排污权初始分配的市场方式比计划方式更具有效率[2]。初始排污权有偿分配（固定价格、拍卖）将成为主要的分配方式[3]。在理论研究方面，文献[4-6]对排污权交易的理论来源和研究进展进行了综述：近年来，对排污权交易的最新研究逐步引入了博弈论和信息经济学、实验经济学、系统规划、拍卖理论、机制设计及市场设计等理论和方法，主要关注于环境外部性及交易成本基础理论研究，以及排污权交易市场中的市场层级划分、排污权总量初始分配、定价机制、市场势力、激励机制、交易成本、企业监督等问题。国内研究主要关注与政策的实用性、初始分配、拍卖定价方式等方面。而对排污权交易市场的稳定性分析尚不多见。

1 非对称演化博弈

以有限理性为基础的演化博弈论是把博弈理论分析和动态演化过程分析结合起来的一种理论，适合于对动态复杂经济系统的描述和分析。其研究对象是随着时间变化的某一群体，目的是为了理解群体演化的动态过程，并解释说明群体如何达到稳定的均衡状态。而排污权交易市场中，产污企业的支付不仅由自己的出价决定，还与竞价对手的出价有关，所以得出的纳什均衡可能有多个，但是仅当市场收敛于唯一的均衡时，市场才是有效的。正是基于此，本文分别就两种不同的初始排污权有偿分配的竞价机制下，对排污权市场的演化情况进行分析，并从市场效率的角度分析对于不同的配总量，如何才能达到稳定的均衡，并提高排污权市场的市场效率。

考虑两个非对称相互博弈的种群Ⅰ和Ⅱ，每一个种群只有两种可供选择的策略L和H，种群中的个体俩俩随机配对进行博弈，其支付矩阵如图1所示[7]：

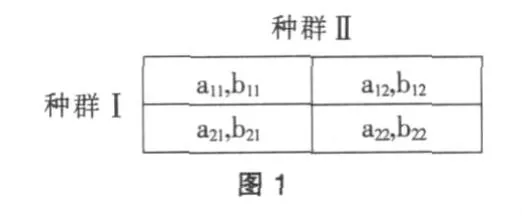
其中，aij（i,j=1,2）表示种群Ⅰ中个体的支付,bij(i,j=1,2)表示种群Ⅱ中个体的支付。其中每一方的支付不仅取决于自身的策略选择，也取决于另一方的策略选择，所以一般情况下aij≠bij(i,j=1,2).记种群Ⅰ和种群Ⅱ选择策略L是比重分别为x1和x2，当种群的学习速度比较慢（即当某一种群改变策略时，另一种群模仿的速度比较慢）时，则由复制动态方程有[8]；

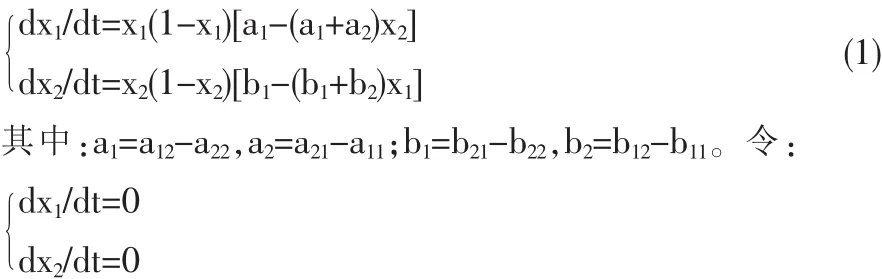
可得系统的局部平衡点为：（0，0），（1，1），（1，0），（0，1），,其中。令 F(x1)=dx1/dt,F(x2)=dx2/dt,根据[8]，Jacobin 矩阵，若|J|且 J的迹（trace）小于零则为 ESS((Evolutionary Stable Strateg);若迹等于零则为鞍点（saddle point）。

2 排污权交易一级市场均衡分析

在排污权交易一级市场中，若参与竞价的产污企业仅有两种类型，低污染治理成本且排放量大的A,高污染治理成本且排放量小的 B.假设市场规定的报价区间为[λ,γ],且 γ＜λ,则参与竞价的产污企业i(i=1,2,……)的最优报价策略为选择报价 bi[λ,γ],使自己的支付或期望支付最大。 不妨记 bi=λ+ai(γλ)，其中αi∈[0,1]，即参与排污交易的产污企业的最优报价策略为在[0,1]上选择αi，使自己的支付或预期支付最大。假设产污企业仅在αi=0，1两个策略间做选择，分别记为策略L和H。A类型产污企业的支付矩阵记为A=（aij），B类型产污企业的支付矩阵记为B=（bij），其中i,j=1,2。假设A类型产污企业有n个，污染物治理成本为c1，排污总量为e1；B类型产污企业有m个，污染物治理成本为c2，排污总量为e2，其中有λ＜γ≤c1＜c2；排污许可证的交易总量为E（假设1单位的排污许可证可以允许排放1单位的相应污染物），且有0＜E＜ne1+me2。 这里假设 ne1＞me2（若 ne1＜me2或 ne1=me2，分析过程类似）

2.1 二级密封拍卖下的演化均衡分析

在二级密封拍卖竞价机制下，A类型产污企业与B类型产污企业同时出价，出价高者中标，但所有成交的排污许可证价格次高的报价统一结算。由前面的假设有e1＞e2,因此有：

(1)当交易的排污许可证的总量E满足ne1＜E＜ne1+me2时，有：

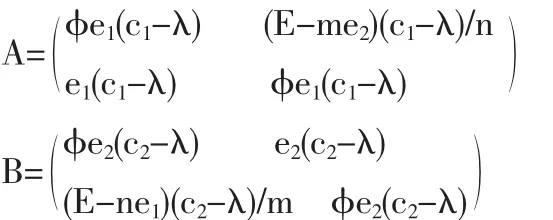
其中 φ=E/ne1+me2，带入公式计算得，a2＞0,b2＞0,a1、b1符号不确定，代入Jacobin矩阵J分析得：

①当 a1＞0 且 b1＞0 时， 平衡点 （1，0），（0，1） 是 ESS；（0，0），（1，1）是不稳定点；为鞍点。

②当 a1＞0 且 b1＜0 时, 平衡点（1，0）是 ESS。 因为 b1＜0，b2＞0,此时有 b21＜b22,b11＜b12,所以 x2=0 即 H 是 B 类型产污企业的占优策略。由 a1＞0，即 a12＞a22，所以x1=1即 L是 A类型产污企业的占优策略，因此（1，0）是唯一的ESS。

③当 a1＜0 且 b1＞0 时，平衡点（0，1）是 ESS，因为 a1＜0，a2＞0，此时有 a12＜a22，a11＜a21,因此 x1=0 即 H 是 A 类型产污企业的占优策略。由 b1＞0，即 b21＞b22，有 x2=1 即 L 是 B 类型产污企业的占优策略，因此（0，1）是唯一的 ESS。

④当 a1＜0 且 b1＜0 时,类似前面的分析可知（0，0）是唯一的ESS。

(2)当交易的排污许可证的总量E满足me2＜E＜ne1时，有：

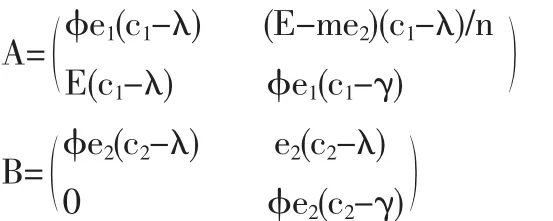
计算有：b1＜0，b2＞0，a1、a2的符号不能确定， 代入 Jacobin矩阵J分析得：

①当 a1＞0 且 a2＞0 时，平衡点（1，0）是 ESS；

②当 a1＞0 且 a2＜0 时，平衡点（1，0）是 ESS；

③当 a1＜0 且 a2＞0 时，平衡点（0，0）是 ESS;

④当 a1＜0 且 a2＜0 时，平衡点（0，0）是 ESS;

(3)当交易的排污许可证的总量E满足0＜E＜me2时，有：

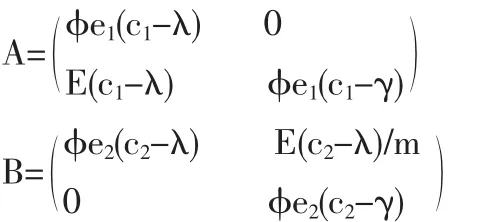
计算有：a1＜0，b1＜0，a2＞0，b2＞0， 代入 Jacobin 矩阵 J 分析得：均衡点（0，0）是唯一的 ESS。

从①～③的分析可知，在报价上限γ≤c1＜c2的前提下，若平衡点（0，0）是唯一的ESS，即两种类型的排污企业均选择报价上限为其报价，则市场效率将达到最高。下面的讨论将假设γ已经给定，讨论市场效率最高时的报价下限λ的取值范围[λ*,γ）。

i当 ne1＜E＜ne1+me2时，仅当 a1＜0 且 b1＜0 时，排污权交易市场的 ESS 为（0，0）；因为 a1=a12-a22=(E-me2)(c1-λ)/n-φe1(c1-γ)

b1=b21-b22=(E-ne1)(c2-λ)/m-φe1(c1-γ)，计算得：

λ*＞max[η1γ+(1-η1)c1,η2γ+(1-η2)c2,]， 其中 η1=ne1E/(E-me2)(ne1+me2)，η2=ne2E/(E-ne1)(ne1+me2)

ⅱ当交易的排污许可证的总量E满足me2＜E＜ne1时，仅a1＜0 时，均衡点（0，0）是排污权交易市场的唯一 ESS。 同上有λ*＞η1γ+(1-η1)c1。

ⅲ当交易的排污许可证的总量E满足0＜E＜m2时，排污权交易市场一定收敛于均衡点 （0，0）， 即 （0，0） 是唯一的ESS。

2.2 一级密封拍卖下的演化均衡分析

在一级密封拍卖机制（现在排污权有偿分配采用最多的机制）下，A类型产污企业与B类型产污企业同时出价，出价高者中标，但所有成交的排污许可证价格按排污企业自己的报价结算。因此有：

①当交易的排污许可证的总量 E满足ne1＜E＜ne1+me2时，有：

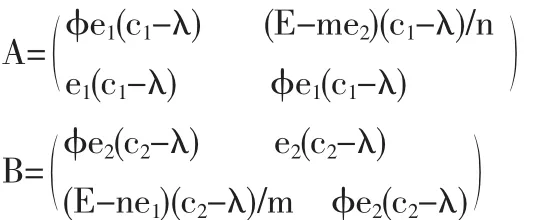
a1、a2、b1、b2符号均不能确定， 当且仅当 a1＜0 且 b1＜0 时，均衡点（0，0）是 ESS，但不唯一。

(2)当交易的排污许可证的总量E满足me2＜E＜ne1时，有：

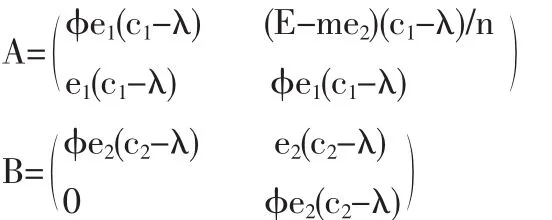
b1＜0,a1、a2、b2符号不能确定，（1，0），（1，1）可能是 ESS,当且仅当 a1＜0 时，均衡点（0，0）是 ESS，（0，1）是不稳定点。

(3)当交易的排污许可证的总量E满足0＜E＜me2时，有：

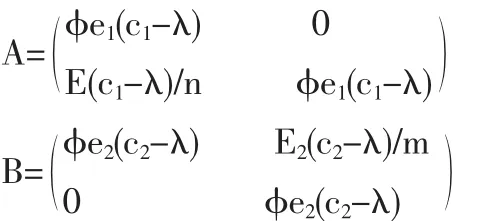
分析得：a1＜0，b1＜0，a2、b2符号不能确定， 即平衡点（0，0）总是排污权交易市场的 ESS，（0，1）、（1，0） 是不稳定点，当a2＜0 且 b2＜0 时，（1，1）是 ESS.这时是鞍点。

由上面的分析知：当 ne1＜E＜ne1+me2时，仅当 a1＜0 且 b1＜0 时，均衡点（0，0）是 ESS，但不唯一。但是，只有（0，0）是唯一的ESS时，排污权交易市场才是有效的。因此，在a1＜0、b1＜0时，为使排污权交易市场一定收敛于（0，0），只有 b2＜0且 b2＜0不成立。

a1、b1＜0 时,计算得：

max[(1-η1)c1+η1γ，(1-η2)c2+η2γ]＜γ*（2），a2＜0 且 b2＜0 不成立时有 λ*＞min[1-1/φ)c1+γ/φ,(1-1/φ)c1+γ/φ]，即只要：

max[(1-η1)c1+η1γ,(1-η2)c2+η2γ]＜λ*＞min[(1-1/φ)c1,(1-1/φ)c2+γ/φ]，此时排污权交易市场唯一收敛于（0，0）。

①当 me2＜E＜ne1时，与上面的分析类似，a1＜0 时,计算得：

(1-η1)c1+η1γ＜λ*，a2＜0 且 b2＜0 不成立时有：

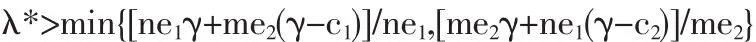
即只要(1-η1)c1+η1γ＜λ*＞min{[ne1γ+me2(γ-c1)]/ne1,[me2γ+ne1(γ-c2)]/me2}，

此时排污权交易市场唯一收敛于（0，0）。

②当 0＜E＜me2时，平衡点（0，0）总是排污权交易市场的ESS，只要a2＜0且b2＜0不成立，排污权交易市场唯一收敛于（0，0）。 这时有：

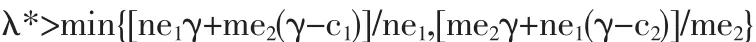
3 结论

本文基于不对称演化博弈原理，分别对一级与二级密封拍卖下的排污权交易市场演化均衡进行分析，并从有利于提高排污权市场效率的角度进行政策分析。分析表明：在两种不同的拍卖机制下，通过选择适当的竞价下限，可诱导排污企业选择竞价上限作为其最优选择，从而带来高的市场效率。运用演化博弈论分析排污权交易市场的均衡，对解释排污权交易的复杂性，动态变化提供了很好的方法和理论依据。随着演化博弈论的日臻完善，它必将对排污权交易市场起着重要作用。

[1]Rose A,Stevens B.The Efficiency and Equity of Marketable Permits for CO2Emission[J].Resource and Energy Economics，1993，15(1).

[2]王先甲,肖文,胡振鹏.排污权初始分配的两种方法及其效率比较[J].自然科学进展,2004,14(3).

[3]King C L,Zhao Jinhua.On the Long Run Efficiency of Auctioned vs.Free Permits[J].Economics Letters,2000,69(2).

[4]李寿德,王家祺，李寿德，王家祺.排污权交易制度的经济学基础分析[J].武汉理工大学学报(信息与管理工程版)，2004,(8).

[5]陈德湖.排污权交易理论及其研究综述[J].外国经济与管理，2004.

[6]张永宏等.排污权交易理论及其发展研究综述[J].辽宁工学院学报，2007，（2）.

[7]张新华,赖明勇.基于演化博弈的电力竞价市场均衡分析[J].管理工程学报，2008,(2).

[8]Daniel Friedman.On Economic Applications of Evolutionary Game[J].Theory Journal of Evolutionary Economics,1998,8(1).

F407.61

A

1002－6487（2011）11－0067-03

（责任编辑/亦 民）