对统计学中几个基本问题的探讨

李从欣 ，李国柱

（1.天津大学，天津 300072；2.石家庄经济学院，石家庄 050031)

对统计学中几个基本问题的探讨

李从欣1，2，李国柱2

（1.天津大学，天津 300072；2.石家庄经济学院，石家庄 050031)

就统计学教学中存在的问题，文章讨论了众数、算术平均数、中位数的关系；标志、指标、变量的关系；组距式分组中的组限归属；连锁替代法的合理性；时间序列变动的分解等。并就以上问题提出了见解。

平均数；变量；统计分值；时间序列

1 众数、算术平均数、中位数的关系

长期以来，人们认为众数、中位数、算术平均数之间存在一定的关系，且这一关系取决于总体内的分布情况。当对称分布时，算术平均数、中位数、众数合而为一，即；在偏态分布的情况下，三者彼此分离，算术平均数、众数分居两边，中位数介于两者之间，若众数在左边，平均数在右边，即，称为正偏分布；若众数在右边，平均数在左边，即，则称为负偏分布。以此为基础还计算了偏度系数，用SK表示：

当SK=0时，分布为对称分布；当XK＜0时，为负偏态；当XK＞0时，为正偏态。如果仅从偏斜方向上来考虑，根据SK判断和根据算术平均数与众数的关系进行判断是一致的。

这一论述在统计学教科书存在了几十年，但更多出于直观判断，并没有明确的理论依据。更确切地说，这一论述并不准确，首先，中位数并不一定位于众数和算术平均数之间；其次，根据众数和算术平均数的大小来判断偏斜方向也不一定准确。以下的例子可以提供很好的证明。

表1为某工厂工人生产某种零件所耗用时间的资料，根据这一资料，可以计算出以下四个统计量的数值：，Me=7，Mo=5，α=-0.127。其中偏度系数α是按矩法计算的。

在这一例子中，中位数并没有介于算术平均数和众数之间，它的取值是最大的；如果根据算术平均数和众数的大小来判断偏斜方向，由于算术平均数大于众数，应该是正偏，但从我们按矩法计算的偏度系数来看，由于α=-0.127，应该是负偏。

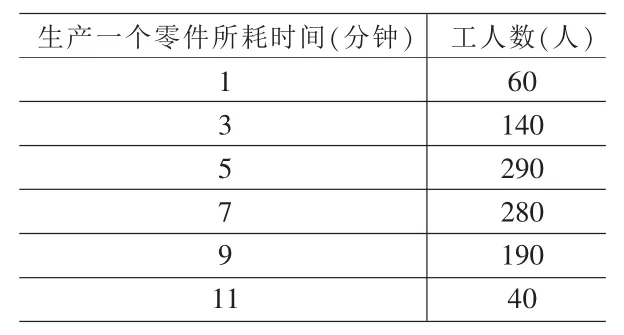
表1 某工厂工人生产某种零件所耗时间分组表

2 标志、指标和变量

标志、指标和变量的概念在统计学教材中也存在了几十年，虽然现在某些教材中已去掉了这些内容，但大部分教材中这些内容仍然存在。标志和指标是基于总体和总体单位定义的，标志是用来说明总体单位的属性或特征的，而指标是从数量方面对总体的规模及其特征的概括说明，变量则被定义为可变的数量标志和指标。按照该定义，品质标志不属于变量，这一定义在在实际应用中产生了诸多问题，尤其是不能和后续课程及人们的日常应用相衔接。以回归分析中的虚拟变量（又称哑变量）为例，在回归分析中，为了分析“质”的因素对因变量的影响，通常设置虚拟变量。如果我们认为不同性别、不同民族、不同政治面目的人消费水平有差异，除了以收入水平作为主要解释变量外，还可以加入虚拟变量解释性别、民族、政治面目的影响。但按照传统的关于变量的定义，性别、民族、政治面目都是品质标志，而不是变量。

解决这一问题有两种思路，一种是去掉标志和指标的定义，国内某些教材已经这么做了。但去掉这对概念也有一个问题，国人使用指标体系这个概念几十年了，且已深入到生活中的方方面面，没有指标何来指标体系呢？因此简单去掉可能不是最好的方法。当然把指标体系改成评价体系、把指标改成要素可避免这一尴尬，并且一些国家也确实是这么叫的。第二种思路是改变变量的定义，把变量定义为标志和指标，而不是可变的数量标志和指标。这既解决了和虚拟变量定义的衔接，也解决了人们使用指标和指标体系的习惯问题。

3 组距式分组中的组限归属问题

在组距式分组中，每组包含许多变量值，每一组变量值中，其最小值为下限，最大值为上限。相邻两组的界限，称为组限。凡是组限不相连的，称为间断组距式分组；凡是组限相连（或称相重叠的），即以同一数值作为相邻两组的共同界限，称为连续组距式分组。如果变量值只是在整数之间变动，可采用间断组距式分组；如果变量值在一定范围内的表现既可以是整数，也可以是小数，只能采用连续组距式分组。在连续组距式分组中，因为以同一个数值作为相邻两组共同的界限，需要人为规定这一界限属于哪一组。国内统计教材通常采用的是“上组限不在内原则”，即凡是总体某一个单位的变量值是相邻两组的界限值，这一个单位归入作为下限值的那一组内。

如果仍然采用手工汇总，这一规定并无不妥之处。但现在普遍采用计算机汇总，如果各统计软件对组限的归属界定不同，就会造成分组结果不同：在某种软件下，某个观察值分到了上一组，但在另一种软件下却分到了下一组。这种情况在现实中确实存在，如EXCEL、Stata软件一般采用“上限在内原则”，而Eviews软件却采用 “上限不在内原则”，至于SPSS软件，则可以在“上限在内”和“上限不在内”之间进行选择。因此在进行统计分组时，必须注明组限的归属问题，但目前的研究报告、论文等并没有重视这一问题。

在实际运用中，还可采用变通的方法，将连续组距式分组重叠的组限变为不重叠。方法就是对一个组的上限值采用小数点的形式，小数点的位数根据所要求的精度具体确定，通常比实际的小数位数多一位。假如数据（保留两位小数）的最小值为3.22，最大值为6.09，如果取组距为0.3，并将比最小值略小一点的数3.20作为第一组的起点，则第一组的上限（也就是第二组的下限）为3.50，为了避免重叠组限的归属问题，可以考虑将第一组的上限值取为3.499，第二组的下限仍然为3.50，即可将重叠组限变换为间断组限。此时，不论采用手工汇总，还是计算机汇总，所得的分组结果都是一致的。

4 连锁替代法的合理性问题

在进行指数因素分析时，通常采用连锁替代法，基本思想是将各因素指标按先数量指标后质量指标的顺序排列，测定其中某个因素的作用时，要将其余所有因素进行固定。即测定数量因素的作用时，要将质量因素固定在基期；而测定质量因素的作用时，要将数量因素固定在报告期。

在实际应用中，连锁替代法存在三个方面的问题。一是计算结果不统一，完全取决于变量的先后顺序；二是没有理论基础，无法说明为什么某个变量先变化，其它的变量后变化。比如销售额的变化究竟是价格变化在先还是销量量变化在先；三是没有考虑变量之间的交互关系，变量之间可能并不是独立变化的，更多的是交互发生作用。

解决这一问题可以采用数学分析中的全增量分析理论，这一方法最早由徐国祥等引入指数分析领域。

对任意二元函数y=f(pq)，其全增量可表示为：

当给出函数的具体形式时，可得到增量的表达式。令，则

这便是指数因素分析法中的绝对量分析，右边第一项为p变动的影响，第二项为q变动的影响，第三项为p和q同时变动的交互影响。

将（3）式两边同除以y0，即可得到指数分析的相对量分析，即

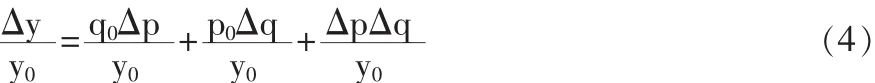
公式（3）、（4）是针对单一商品（或个体指数）的，如要进行综合指数的因素分析，只要对（3）、（4）稍加变形，在方程两边加上求和符号即可。

综合指数因素分析的绝对分析和相对分析如下：

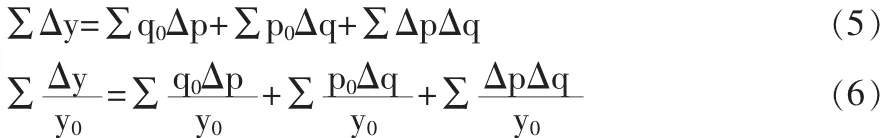
这种方法解决了连锁替代法的三个问题：计算结果和变量排列顺序无关；存在理论基础，完全符合因素分析应从基期出发的原则；考虑了两个变量同时变动的交互影响。

5 时间序列变动的分解问题

统计学教材讲授了时间序列的分解，但没有涉及时间序列变动的分解。时间序列分解存在两种模型，即乘法模型和加法模型。时间序列变动的分解也基于这两种模型。

5.1 基于乘法模型的时间序列变动分解

经济时间序列的变化受许多因素的影响，概括地讲，可以将影响时间序列的因素分为四种，即长期趋势、季节变动、循环变动和不规则变动。时间序列的分解方法有很多，较常用的模型有加法模型和乘法模型两种。如果认为各因素之间独立发生作用，可采用加法模型；如果认为各因素之间交互产生作用，通常采用乘法模型。

乘法模型的基本形式为：

基于乘法模型的时间序列变动分解可采用增量分析法，将公式（2）应用于多元函数，时间序列的增量可表示为：

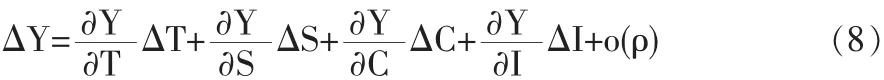
结合公式（7），公式（8）可以进一步表示为：

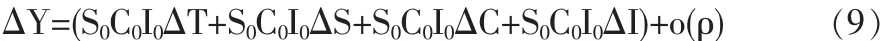
方程右边括号中的四项分别为四个因素单纯变动的影响，最后一项为交互影响值，包括两因素同时变动影响、三因素同时变动影响和四因素同时变动影响。在一般情况下，为了便于分析，只需列出一个总的交互影响即可。

将（9）式两边分别除以Y0，可得相对分析表达式。

5.2 基于加法模型的时间序列变动分解

时间序列加法模型的基本形式为：

根据（10）式，可得增量恒等式：

将（11）式两边分别除以Y0，可得相对分析表达式：

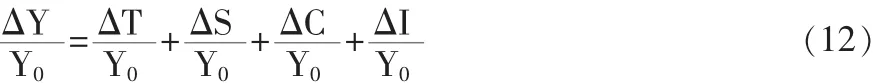
对公式（12）进行适当变形，可得

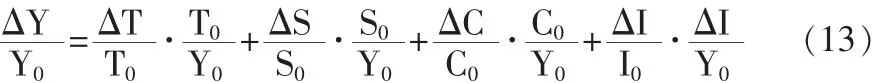
公式（13）为各因素对时间序列拉动作用的量化公式。公式（12）、（13）分别从不同角度分析了各因素对时间序列变动的影响。

[1]刘德智.统计学[M].北京：清华大学出版社，2007.

[2]黄良文.统计学原理[M].北京：中国统计出版社，2003.

[3]贾俊平.统计学[M].北京：中国人民大学出版社，2000.

[4]徐国祥.统计学[M].上海：上海人民出版社，2007.

C81

A

1002-6487（2011）11-0041-02

李从欣（1974-），女，河北无极人，博士研究生，研究方向：区域经济统计。

（责任编辑/浩 天）