基于企业战略的多项目资源配置优先级评价

曾玉成 ，李敏榆 ，曾 粟

(1.四川大学 工商管理学院，成都 610064；2.广州固源电力设计公司，广州 511400)

基于企业战略的多项目资源配置优先级评价

曾玉成1，李敏榆2，曾 粟1

(1.四川大学 工商管理学院，成都 610064；2.广州固源电力设计公司，广州 511400)

文章针对当前企业缺乏基于战略的多项目资源配置优先级评价理论与方法等问题，以实际调查资料和数据为依据，设计了基于战略的多项目资源配置优先级评价指标体系；并针对当前的优先级评定方法较为复杂的现实，构建了新型的“STL—AHP”优先级评定方法；以某企业多项目管理为例验证了该方法的可行性，为企业多项目资源配置优先级评价提供了有益的参考。

企业战略；多项目管理；资源配置；优先级评价

0 引言

企业多项目资源配置优先级评价，是以企业战略为指导，对企业拟选的所有项目进行综合分析与判断，按与企业战略耦合程度的高低对项目进行先后排序，为企业对多项目进行资源配置提供依据。但是，如何科学评价或确定企业多项目优先级，尤其是基于战略的多项目资源配置优先级，企业界正处在探索当中，而理论界也缺乏这方面的深入研究。

目前，对企业多项目资源配置优先级评价研究较少。在笔者查到的为数不多，而具有一定代表性的文献中，易明等人基于平衡计分卡和熵权法思想，提出了铁路建设项目的优先级评价方法，但计算方法不够详尽；单汨源等提出了RAGA—AHP法的项目优先级评定改进方法，但仍然主观性较强，而且计算也较繁锁，不利于在企业中的实际应用；谭云涛等提出了应从企业的战略角度对项目机会进行优先排序，但并未具体的评价方法；李元元等人提出了基于熵权的改进TOPSIS法，虽然减少了主观性，但若操作者缺乏经验，有可能偏离实际；熊健等提出了一种基于多属性群决策的需求优先级排序方法，虽然对专家打分具有较好的指导作用，但是计算较为麻烦；高亮等提出了基于遗传神经网络评价铁路多项目优先级的方法，虽然为多项目优先级评价方法增加一种新方法，但计算仍然较为复杂。就现有的研究来看，主要是对项目层面上的多项目优先级评价的研究，评价主要以财务收益为主要评价指标，注重企业的短期收益，忽视了企业层面，尤其是基于企业战略的多项目资源配置优先级评价方法的研究；同时，研究也过于理论化，缺乏实证方面的深入探索。

1 企业多项目资源配置优先级评价指标体系的构建

针对当前缺乏战略层面的优先级评价体系等问题，通过实地调查，笔者提出构建战略主导型优先级评价体系，即以企业发展战略为主线构建企业多项目资源配置优先级评价指标体系。一级指标主要包括：

（1）战略与项目耦合度；

（2）项目风险程度；

（3）财务优劣程度；

（4）竞争优势程度。

在以上的指标中，项目的创新程度，是所有指标中得分最低，尽管不可能单独设立为一个考核指标，但是，考虑创新性是一个企业能否具有竞争优势的重要因素，因而应作为评价项目竞争优势的重要指标。所以，企业多项目资源配置优先级评价指标体系由战略与项目耦合度、项目风险程度、财务优劣程度和竞争优势程度4个一级指标以及所包含的12个二级指标构成，详见表1。

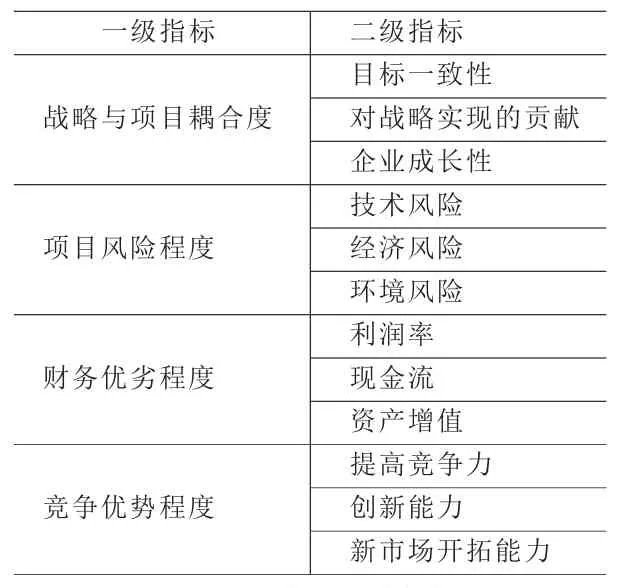
表1 企业多项目资源配置优先级评价指标体系

2 企业多项目资源配置优先级评定方法

2.1 STL—AHP优先级评定方法构建

针对企业多项目资源配置进行优先级排序难于用定量分析，缺乏统一的优先级的评价方法，尤其是在各项目所处的环境各不相同，具体数据可能相差不大，但代表的意义却相差甚大等问题，笔者提出将企业战略与现有的层次分析法相结合而形成一种新的计算方法，即战略主导型（strategy to lead，STL）—层次分析方法 (Analytic Hierarchy Process，AHP)相结合，构建“STL—AHP”优先级评定方法。

笔者提出构建 “STL—AHP”优先级评定方法，就是将AHP具体的计算理论和企业战略管理理论以及项目所处行业的特点结合起来，通过实际调查，构建适合实际情况的一种新的计算方法。该方法以企业战略为指导，在建立判断矩阵和权重设计时考虑了一致检验的要求，并侧重战略的权重评分，总的来说，“STL—AHP”优先级评定方法与AHP法最大的不同在于，在原有AHP法的具体计算评价范畴基础上，采用了更高层次的STL—AHP法对项目进行评价，强调了战略与项目的耦合性。因为有了战略作为导向，在用STL—AHP法对项目进行评价而选择结构层次指标时，各个企业就会根据自身的实际情况选择对战略目标的实现影响较大的指标，而忽略一些不太重要的指标，使指标的选择更有针对性，减少因指标选择的不合理导致评价结果对实际行动的误导作用。同时，在选择评价指标进行计算时，也考虑了可能因为应用某些指标的重要性而导致评分越高，则对战略目标实现产生越大的负作用这种情况的发生，故将这些指标作负分处理，而不是全部指标都作正分处理。例如对项目普遍存在的风险问题作负分处理，以在项目总分计算中显示项目风险对项目的影响。另外，针对项目变化发展快的特点评价时，以每月评价一次为基准进行资源配置的调整，以应对项目的变化做出快速的反应。这既有利于解决当前优先级评价中存在的不足，也有利于克服对项目只进行一次评价的僵化做法，强化了评价的合理性，也提高评价的灵活性，使项目能及时得到调整，避免严重偏离战略方向。

2.2 STL—AHP优先级评定方法计算理论

STL—AHP的应用主要分为四个步骤：（1）建立结构层次准则体系；（2）通过专家咨询等方法确定层次结构的分层判断矩阵群；（3）进行层次单排序及其一致性检验；（4）确定方案总排序及其一致性检验。

STL—AHP中各指标的相对评分标度值为1～9分，其中1分代表两个元素相比，具有同等重要性；3分代表两个元素相比，前者比后者稍重要；5分代表两个元素相比，前者比后者明显重要；7分代表两个元素相比，前者比后者强烈重要；9分代表两个元素相比，前者比后者极端重要；2、4、6、8分则代表重要性介于各分值之间。

STL—AHP的具体计算步骤如下：

（1）分别建立各项目的一级指标原始判断矩阵，二级指标作为对一级指标评分时的具体衡量标准。

（2）将原始判断矩阵按列归一化，即先把每一列元素加和，得到列总和，再用列总和去除该列各元素，经过归一化处理后的矩阵就转化为标准判断矩阵。

（3）得出标准判断矩阵后，求出其各列元素的平均值，这些平均值，就是对应行元素的相对权重值。

（4）进行一致性检验。

①将原始判断矩阵的每一列元素都乘以该列元素的相对权重值，再按行相加，产生一加权列向量。

②将加权列向量中的各元素，分别除以对应的相对权重值。

③对上一步所得值相加求平均值，该平均值就是原始判断矩阵的最大特征根λmax。

④按下列公式计算一致性指标CI：

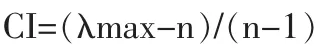
式中，n表示该判断矩阵所含决策元素的个数。

⑤查表得相应的平均随机一致性指标RI，并计算一致性比例CR:

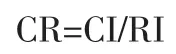
当CR＜0.1时，认为判断矩阵的一致性是可以接受的；当CR≥0.1时，决策者需要对矩阵作恰当修正。

（5）对备选择方案进行排序，计算方法是将每个准则的权重乘以相对于该准则每个方案的权重，然后加总求和，按分值从高到低进行排序。

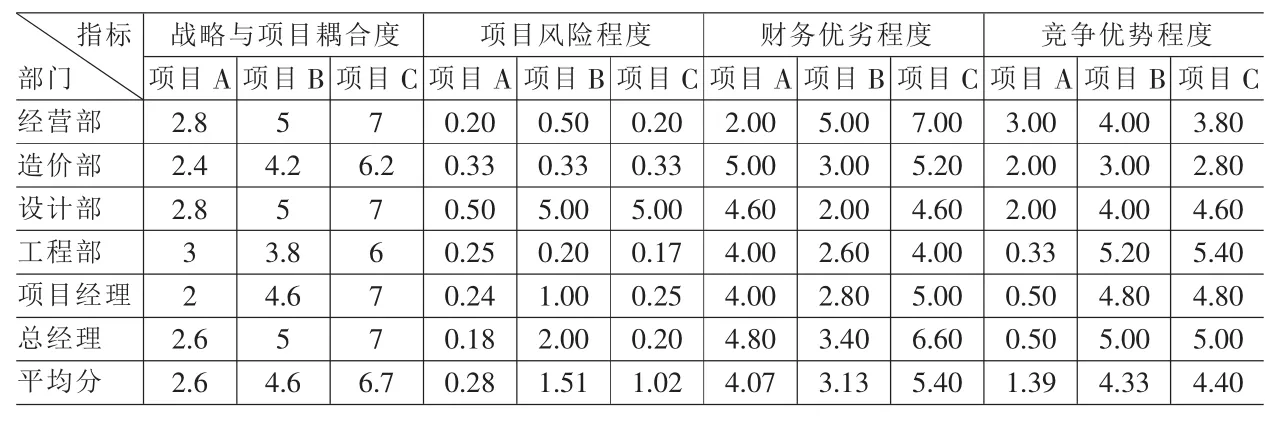
表2 各项目的各项指标的AHP标度值

2.3 STL—AHP优先级评定方法的应用

下面将用三个项目进行STL—AHP的实例计算，三个项目分别是H电站10kV线路设计施工总承包 （项目A）、D矿业35kV线路设计施工总承包（项目B）和L变电站（220Kv）综自改设计施工总承包（项目C）。其中指标层代表准则层，项目层代表方案层。

（1）建立结构层次指标体系

根据优先级评价指标建立结构层次指标体系，详见表3。

（2）确定层次结构的分层判断矩阵群

①由各职能部门负责人、项目经理和企业领导人对项目A、B、C各指标进行相互对比评分。

因为企业经常有很多项目是很类似的，作两两相互对比时，其得分不会相差很大，所以将STL—AHP的标度值标准再细分到0.1分，每0.1分或0.2分代表各指标中的细分指标对比结果，这样既可明确各指标进行对比的内容，又可提高AHP验算的有效性，见表2。

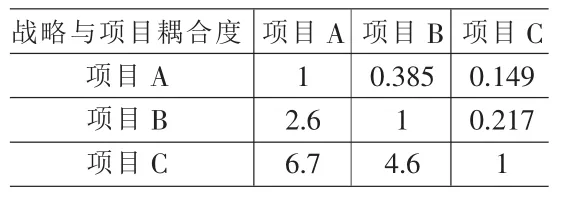
表3 战略耦合度指标的原始判断矩阵

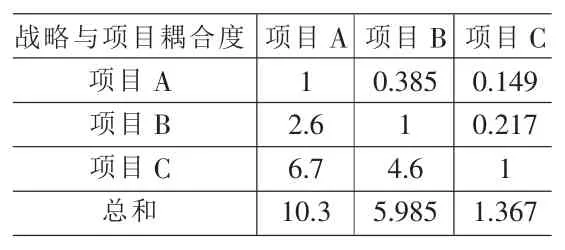
表4 战略耦合度指标的各列相加矩阵

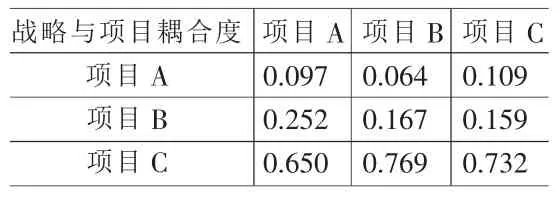
表5 战略耦合度指标的标准判断矩阵

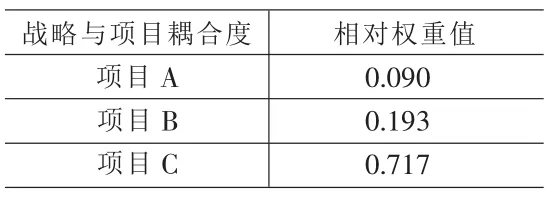
表6 各项目战略耦合度指标的相对权重值

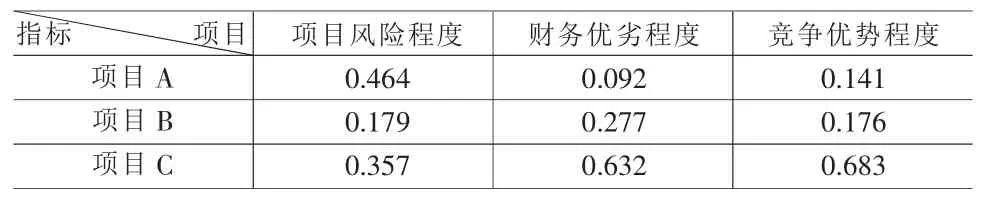
表7 各项目风险程度、财务优劣度和竞争优势度指标相对权重值

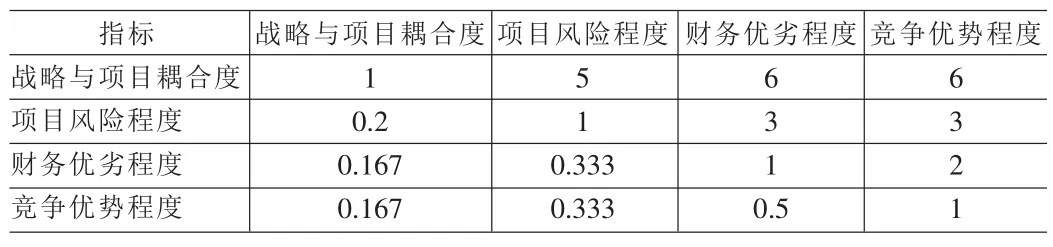
表8 指标间原始判断矩阵

表9 各指标间的相对权重值

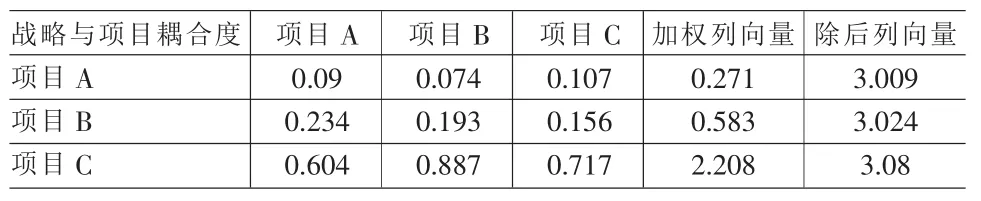
表10 战略指标的最大特征根计算

②以战略指标为例建立原始判断矩阵。

将表2中战略与项目耦合度指标下各项目的对应平均分按两两对比的原则列成下列原始判断矩阵，见表3。

③将表2矩阵中的数值按列相加，得各列总和，见表4。

④将表3原始判断矩阵中的各项数值除以表4对应的各项总和，得标准判断矩阵，见表5。

⑤将表5中的各列相加并取平均值，得各项目战略耦合度指标的相对权重值，见表6。

⑥按以上计算过程可得各项目其余指标的相对权重值，见表7。

⑦按以上计算过程可得各指标的相对权重值，见表9。

（4）进行层次单排序及其一致性检验

这里选择对战略指标进行一致性检验

①将原始判断矩阵的每一列都乘以该列元素的相对权重值，然后按行相加，产生一加权列向量，再分别除以对应的相对权重值，最后求出三个列向量，求其平均值，即为最大特征根，见表10。

最大特征根：（3.009+3.024+3.08）/3=3.038

②计算一致性指标CI：

CI=（最大特征根—N）/（N—1）=（3.038—3）/（3—1）=0.019

③查表得相应的平均随机一致性指标RI为0.58，计算一致性比例CR：

CR=CI/RI=0.019/0.58=0.033＜0.1

当CR＜0.1时，认为判断矩阵的一致性是可以接受的，当CR＞0.1时，决策者需要对矩阵恰当修正。

④同理可得其余指标的CR：

风险程度：CR=0.075＜0.1，风险指标一致性检验通过

财务优劣程度：CR=0.072＜0.1，财务指标一致性检验通过

竞争优势程度：CR=0.009＜0.1竞争性指标一致性检验通过

（5）对各项目得分进行计算，计算方法是每个指标的权重乘以相对于该指标每个项目的权重，然后加总求和，其中风险评分作负分处理，再按分值从高到低进行排序：

项目 A得分：0.09*0.618-0.464*0.204+0.092*0.105+0.141*0.072≈-0.019

项目 B得分：0.193*0.618-0.179*0.204+0.277*0.105+0.176*0.072≈0.125

项目 C得分：0.717*0.618-0.357*0.204+0.632*0.105+0.683*0.072≈0.486

由以上得分可知：项目C＞项目B＞项目A。

所以，由此得出结论，上述三个项目的资源配置优先级排序为第一位次为项目C，第二位次为项目B，第三位次为项目A。

3 STL—AHP优先级评定方法的优势

从以上的分析可以可知，STL—AHP优先级评定方法，具有以下几个方面的优势：

（1）构建了系统的评价指标体系。通过实地调查，构建了战略主导型的优先级评价理论与方法，也为企业多项目资源配置优先级评价提供了系统的评价指标体系。

（2）评价方法简便实用。该方法尽量去掉了比较繁锁的计算环节，力求简便易懂，容易操作，因而适用强，克服了采用其它方法计算较为繁锁的现象。

（3）定性分析与定量分析相结合。即使项目在没有定量数据的情况下，通过项目间的两两对比，也能得出优劣，为不能完全提供定量数据的评价提供了科学的依据。

（4）有利于企业的战略目标的实现。强调了项目与战略的耦合程度，因此，凡是被筛选出来的项目，都与企业战略有较强的耦合程度，有利于企业战略目标的实现。

（5）有利于资源的合理配置。避免了主观经验或人为因素对资源配置的干扰，计算的结果较为客观公正，既有利于对所有项目进行资源的合理配置，又有利于解决资源配置中的各种矛盾。

4 结束语

如何在项目众多、资源有限的情况下合理配置资源，一直是企业面临一个较大难题。针对这个问题，笔者先后调查了近300企业，形成了基于战略的优先级评价指标体系，构建了STL—AHP优先级评定方法。实证表明，该方法简便实用，为企业多项目资源配置确定优先级提供了一种新的评定方法。

[1]易明，周国华，张洁.基于熵权的铁路建设多项目优先级评价[J].铁道运输与经济，2007,(10).

[2]单汨源,张丽,吴娟.基于RAGA—AHP法的项目优先级评定研究[J].科技管理研究，2008,(3).

[3]谭云涛，郭波，郑敏.企业多项目管理中的优先排序问题研究[J].管理工程学报,2005(增刊).

[4]李元元,周国华,韩姣杰.基于熵权的改进TOPSIS法在多项目优先级评价中的应用[J].统计与决策,2008,(14).

[5]高亮,曾庆煌.基于遗传神经网络评价铁路多项目优先级[J].交通科技与经济，2009,(3).

F279.23

A

1002-6487（2011）11-0038-03

国家自然科学基金资助项目（50579101）；国家863重大项目（2008AA04A107）

曾玉成（1966-），男，四川自贡人，副教授，研究方向：企业管理、项目管理。

李敏榆（1973-），男，广东化州人，硕士，研究方向：项目管理。

曾 粟（1983-），男，四川宜宾人，硕士研究生，研究方向：项目管理。

（责任编辑/亦 民）