基于协整与ARMA组合模型的居民中长期消费贷款预测

李运蒙，钱 鑫

(五邑大学 经济管理学院，广东 江门 529020)

基于协整与ARMA组合模型的居民中长期消费贷款预测

李运蒙，钱 鑫

(五邑大学 经济管理学院，广东 江门 529020)

文章运用协整回归与ARMA组合模型，通过房屋销售价格指数对居民中长期消费贷款进行了短期预测。先用2007年1月至2010年1月的37期数据进行Granger因果关系检验，再运用协整回归和ARMA组合建立预测模型，模型对2010年2月至6月共5期的居民中长期消费贷款进行预测，与实际数据相比，预测相对误差小于1.5%，最后提出了一些相关的政策建议。

预测；ARMA模型；协整；居民中长期消费贷款；房屋销售价格指数

0 引言

国内外许多学者对银行信贷问题作了多方面的研究。一些学者根据银行信贷数据的变化特点寻找其规律，建立了预测模型。李宇嘉，陆军(2007)应用马尔科夫链预测理论构建了预测贷款准备金模型[1]，文章认为模型可以作为改革贷款准备金政策的参考。蒋佐斌，谢双琴，张欢(2010)以我国银行2007～2010年月度贷款规模总额为基础数据，建立了银行贷款规模时间序列ARIMA模型[2]，认为其模型对预测值和实际值拟合程度较高，对金融机构进行决策有重要参考价值。另一些学者研究了影响银行贷款变化的重要因素，通过这些因素对银行贷款趋势进行分析，Gerlach and peng(2005)利用香港1982年4季度至2001年4季度的季度数据，实证分析了银行贷款与房地产价格之间的波动关系[3]，认为房地产价格的波动影响银行的信贷扩张，而银行贷款却不影响房地产价格，从而可以利用房地产价格的波动来分析预测信贷波动的趋势。

在商业银行的信贷业务中居民中长期消费贷款作为个人贷款中的重要类别，由于其收益期长、不良率低、综合效益显著等特点，长期以来倍受商业银行的重视。然而，笔者通过实证分析，表明其贷款的规模在某特定的时期随着房价的波动而波动，而房产市场价格在近几年连续上升后，积累了一定的风险，房价与贷款的关联性问题，有待进一步研究。笔者将利用房屋销售价格指数，通过协整与ARMA组合模型，对居民中长期消费贷款数据进行分析和预测。

1 协整与ARMA组合预测模型简介

协整理论是Engle和Granger在1987提出的[4]，对非平稳序列的建模提供了一种新的方法。所谓xt和yt是协整的，要满足下列条件：(1)xt和yt都是I(1)的，即它们是非平稳的，而其一阶差分是平稳的；(2)存在某个线性组合αxt+βyt是I(0)的，且具有零均值，则 xt和 yt具有协整关系，(α，β)为协整向量。

1.1 基于协整与ARMA组合模型的预测思路

变量之间协整关系表示长期均衡关系[5]，建立在这种长期均衡关系上的预测将具有长期规律的特点。一般协整回归通常建立的是同期变量的关系，而要利用协整回归方程进行预测，如利用xt对yt进行预测，需要建立当期被预测变量与其它变量滞后若干期的回归方程，本文建立的是xt-1和yt的协整回归方程，即xt-1和yt的长期均衡方程。通常认为长期均衡关系往往需要在短期的误差修正下得以维持，误差修正使得模型在短期内更好地逼近实际值；而误差修正模型建立的只是滞后一期的模型，且包含当期值xt，不适合建立预测模型，且误差精度难以进一步提高。

本文的思路是首先利用部分数据建立xt-1和yt的长期均衡协整回归方程，由于误差项平稳，若具有序列相关性，可对误差项建立更加精确的ARMA模型，最后再利用另外部分的数据对yt的实际值进行预测检验。分析从Granger因果检验开始，先看看二者有没有预测关系，再进行长期均衡协整关系和ARMA模型等分析。

1.2 相关理论介绍

(1)Granger因果检验。Granger因果关系检验的基本思路是:如果X变量有助于预测Y变量，即在Y的过去值回归中，添加X的过去值作为独立变量，可以显著增加回归的解释能力，则X是Y的Granger原因。检验方法如下：

式中：p为最大滞后阶数。检验的原假设是序列X不是序列Y的Granger原因，即βt=0。如果不能拒绝假设，则序列X不是序列Y的Granger原因；如果拒绝假设，则序列X是序列Y的Granger原因。

(2)协整检验，关于协整关系检验与估计的方法主要有Engle-granger两步法和Johansen极大似然法。

(3)自回归移动平均模型(ARMA)，ARMA(p,q)模型是指模型的自回归过程的阶数为p，移动平均过程的阶数为q,一般式为：

其中μt是方程的残差项。

ARMA模型的适用条件是序列平稳，而协整则将不平稳的序列组合成平稳序列，适合建立ARMA模型。

2 实证分析

2.1 数据选取与处理

为了分析居民中长期消费贷款与房屋销售价格的关系，选取居民中长期消费贷款(dk0)和全国房屋销售价格指数(fj)两个变量作为研究对象，居民中长期消费贷款来源于中国人民银行数据库的月度数据，数据提取时间段为：2007年1月～2010年6月,原始数据如表1所示。房屋销售价格数据来源于清华金融研究中心数据库月度数据，数据提取时间段为：2007年1月～2010年6月。房屋销售价格指数原始数据为按月环比指标(即上月为100)，为使两个指标有可比性，将居民中长期消费贷款2007年1月指标设为100，后续各期折算为上月为100的环比指标，记为dk，两个指标的环比数据结果如表2所示。

同时为了使模型的设定更合理并减少或消除潜在的异方差问题，本文对所有序列取自然对数处理记为和。对于，由于其短期波动性比较大，为更好地反映其规律性，对做一次指数平滑处理，结果记为，平滑处理运算为：处理后运用Eviews5.0绘制lndks与lnfj的折线图如图1所示：

表1 居民中长期消费贷款dk0原始数据(2007.01-2010.06) 单位：亿元

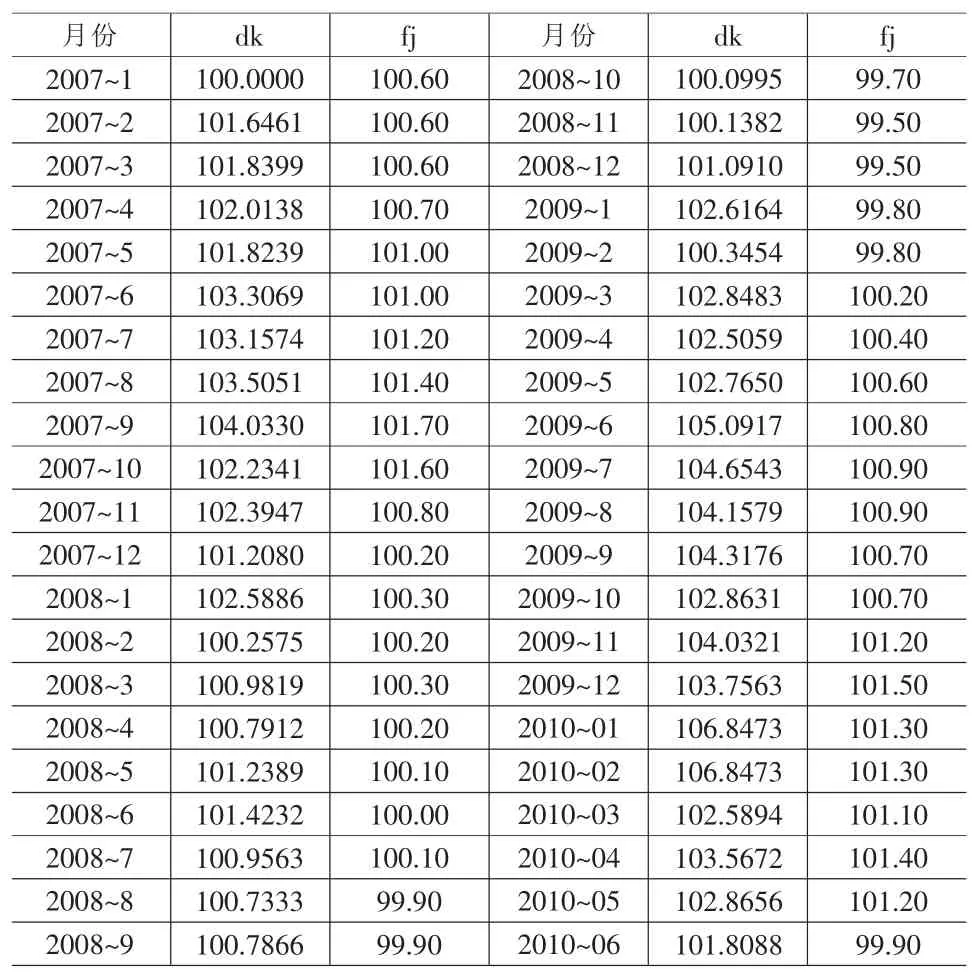
表2 居民中长期消费贷款环比dk与全国房屋销售价格指数fj（2007.01-2010.06）

表3 Granger因果关系检验结果

由图1直观上可以看出：居民中长期消费贷款与房屋销售价格（均用二者环比指标）变化趋势几乎是一致的，由此可以猜测二者可能具有某种关联关系。以下选取表1中的前37个数据，建立预测模型。

2.2 Granger因果关系检验

对居民中长期消费贷款和房产销售价格指数进行Granger因果检验，选最佳滞后期为6，结果如表3，由表3可知，在95%的置信水平下，房产价格是引起居民中长期消费贷款变化的原因，表明二者存在预测关系。

2.3 单位根平稳检验

在进行对序列lnfjt-1和lndkst的ADF单位根检验如表4。表4中滞后阶数的选择原则采取AIC准则，检验形式中的c和t表示带有常数项和趋势项，k表示差分项的滞后阶数。由表4可以看出lnfjt-1和lndkst是I(1)的，即一阶单整的。

2.4 协整检验与协整预测模型的建立

为预测的需要，将采用滞后一期的房屋销售价格指数来预测居民中长期消费贷款，使用滞后协整来建立模型。采用Engle-Granger两步法检验居民中长期消费贷款与房屋销售价格指数之间可能存在的协整关系。

第一步：建立最小二乘回归模型：

表4 ADF检验数据结果

表5 残差 μt的ADF检验

表6 还原后的原始值的预测值与实际值（单位：亿元）

ADR2=0.5146，AIC=-6.4207，D.W.=0.3969，t统计量通过1%显著性检验，F统计量=36.05，F统计量P值=0.0000。

第二步：对模型生成的残差进行单位根检验：

由表5可知，残差序列μt为零阶单整 （小于5%临界值），即 I(0)的，再由(1)式知存在lnfjt-1和lndkst的一个线性组合是平稳序列，故lnfjt-1和lndkst具有协整关系。但由ADR2值可知拟合情况不是太好，不过误差项的自相关性提供了建立更高精度的机遇，下面尝试对误差项运用ARMA建立模型。运用Eviews5.0绘制μt的相关和偏相关图，如图2所示：

可见，μt的偏相关和相关图均是拖尾的，适合建立ARMA模型。下面对μt进行ARMA模型估计，去掉不显著项，最终得到如下表达式：

ADR2=0.6393，AIC=-7.4935，D.W.=1.9760，t统计量通过1%显著性检验，且μt的残差εt的偏自相关系数和自相关均不显著，其残差接近白噪声序列。至此长期关系由(5)式确定，短期关系由(6)式确定。

3.6 模型的计算过程

建立模型时采用的是用2007年1月～2010年1月的37期数据，预测要先计算38期至42期的lndks，再根据(4)式计算lndk，再计算出dk的值，最后还原为dk0的值。

(1)预测估计方程的建立

根据式(5)与式(6)得出第38期的预测式为：

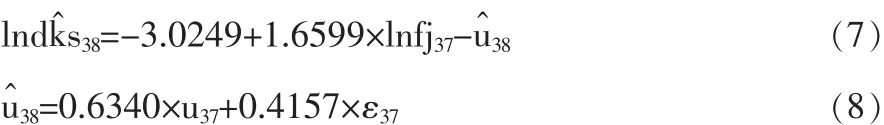
由(7)，(8)式得最终式为：

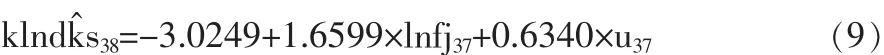
由于37期的各个数据为已知，容易算出lndks的38期的估计值。

第39期使用的数据计算推导过程如下：

后续各期推导方法类似。

(2)预测结果

根据公式逐步计算出2010年2月～2010年6月的居民中长期消费贷款估计值，然后和真实值进行对比，最后计算出预测精度。

由表6可见误差精度均在1.5%的范围之内。

4 结论与建议

本文对居民中长期消费贷款与房屋销售价格的协整关系进行了实证分析并对居民中长期消费贷款进行了预测，可以得到如下结论：

（1）居民中长期消费贷款环比与房屋销售价格（滞后一期）环比之间存在协整关系，即长期均衡关系，同时房屋销售价格环比是居民中长期消费贷款环比的Granger原因，即反映出在所选取的数据区间内，房屋销售价格环比可以用来预测居民中长期消费贷款环比数据。

（2）预测模型在考虑长期规律和短期波动的同时，充分考虑了实际数据的内在特性，并用于改善模型的精度。在存长期均衡关系的前提下，为提高预测精度，利用协整回归方程误差项的相关性，建立误差项的预测ARMA模型，并将其纳入整个模型之中。最终模型的模拟误差为白噪声序列，预测误差精度在1.5%范围之内。

（3）预测模型是以居民中长期消费贷款环比与房屋销售价格环比数据进行建模，并将最终预测结果还原为实际数据。而环比数据可以看作相应经济指标的波动指标，如大于100表示向上波动，小于100表示向下波动，二者的协整关系表示居民中长期消费贷款与房屋销售价格的波动具有长期均衡关系，并且由图1和(5)式可以看出二者的波动方向相同。

（4）居民中长期消费贷款与房屋销售价格之间具有长期的均衡关系，还可以表明在所考虑的问题区间居民中长期消费贷款中的住房按揭贷款占据可观的比重，因为房价与住房按揭贷款直观上看更密切。这一结论与目前多数居民的长期贷款一般为住房贷款的现实相符。

最后，通过房价的波动来预测贷款的波动可以为银行放贷提供一定程度上的依据，从而为制定房贷政策和防范金融风险提供一定程度的帮助。在某些情况下，房价在短期内大幅度升高，源于房产市场的过度投机，房价的升高意味着房产风险增大，房贷也会有很大的风险，此时应该及时控制房贷规模；而房价在另外一些情况下可能被低估，具有投资价值，房贷有益于银行发展，应支持房贷规模的扩大。采取适当的方法对未来贷款的变化进行预测，有利于充分把握市场变化趋势，提前或适时制定出防范风险的相关政策，更好地防范潜在的风险，促进信贷的良性发展。

[1]李宇嘉，陆军.风险溢价、预期损失与预测贷款损失准备金[J].当代财经，2007，(12).

[2]蒋佐斌，谢双琴，张欢.ARIMA模型在银行贷款规模预测中的应用[J].金融与经济,2010,(7).

[3]Stefan Gerlach，Wensheng Peng.Bank Lending and Property Prices in Hong Kong[J].Journal of Banking&Finance,2005,(20).

[4]Engle，Robert F.,C.W.J.Granger.Co-integration and Error Correction：Representation，Estimation，and Testing，Econimetrica[J].Journal of Econimetrica,1987,(55).

[5]高铁梅,王金明,梁云芳,刘玉红.计量经济分析方法与建模-EViews应用及实例(第二版)[M].北京:清华大学出版社，2009.

F832.479

A

1002-6487（2011）11-0061-03

广东省自然科学基金项目（8152902001000010；9452902001004060）

李运蒙（1964-），男，山东郓城人，副教授，硕士，研究方向：金融市场数据分析与建模。钱 鑫（1984-），男，河北秦皇岛人，硕士研究生，研究方向：金融市场数据分析。

（责任编辑/亦 民）