和频与差频振动光谱实验构型的分析模拟

2011-12-11邓罡华

物理化学学报 2011年12期

关键词：射角入射光入射角

汪源邓罡华郭源,*

(1海南大学三亚学院理工分院,海南三亚572022;2中国科学院化学研究所,分子反应动力学国家重点实验室,北京100190)

和频与差频振动光谱实验构型的分析模拟

汪源1邓罡华2郭源2,*

(1海南大学三亚学院理工分院,海南三亚572022;2中国科学院化学研究所,分子反应动力学国家重点实验室,北京100190)

实验构型分析是定量分析和频振动光谱的基础.变换实验构型,不仅要考虑某一振动模式信号强度的大小,还要考虑不同构型下的信号检测效率.现有的和频振动光谱实验构型分析主要考虑前者.本文探讨实验构型分析中所涉及的信号检测效率问题,模拟在共向式和频(差频)及对射式和频(差频)振动光谱实验中选取何种实验构型对采集信号光更加合理有效.利用相干光学过程能量守恒和动量守恒原理,分析了入射角及入射光频率等因素对信号出射角的影响,并模拟了信号出射角与入射角及入射光频率的关系,得到了可选的入射角组合最多、出射角随入射光频率变化最小的实验构型.结果表明,和频振动光谱采取共向式实验构型,差频振动光谱采取对射式实验构型,有利于信号采集,进而有利于用实验构型分析方法对和频(差频)振动光谱进行定量研究.

非线性光学;实验构型分析;和频振动光谱;差频振动光谱

1 引言

界面及界面上由分子构成的有序分子膜体系一直是自然科学研究的前沿课题之一,是物理学、化学、生物学、材料科学研究的交汇点,也是最新科学与技术研究成果的集中展示.1界面研究的技术手段在最近几十年获得长足进展.2-5本文仅涉及其中二阶非线性光学方法的实验构型分析.

二阶非线性光学方法包括二次谐波(SHG)、和频振动光谱(SFG-VS)与差频振动光谱(DFG-VS).在偶极近似下,二阶非线性光学过程对于具有反演对称的体相介质是禁阻的.由于界面是对称破缺的,所以在界面上二阶非线性光学过程是允许的.从某种意义上说,二阶非线性光学技术具有“与生俱来”的界面选择性和界面灵敏性.此外,二阶非线性光谱还具有高的光谱、时间和空间分辨,是研究界面反应动力学的理想工具.近二十年来,二阶非线性光学方法的理论和实验技术取得重大进展,已成为界面研究的重要手段之一.6-12二阶非线性光学光谱可以提供界面分子有序度、取向、取向分布、分子的电子光谱、振动光谱及界面分子反应动力学等各种信息.6,13SHG主要用于探测界面分子的电子光谱,可提供界面分子偶极跃迁的信息;SFG和DFG可以探测界面分子的振动光谱,得到界面分子基团的信息.SHG和SFG(DFG)是两种互为补充的非线性光学方法.SFG和DFG在研究界面振动光谱时,也互有所长.在某些实验条件下DFG-VS可替代SFG-VS用于探测界面分子的振动光谱.此外,相对于SFG-VS,DFG-VS有其独特的性质.从DFG-VS产生的金属或电极表面吸附分子的差频光谱信号可以得到与SFG信号不同的相位信息,这对于研究金属或电极表面吸附分子有重要意义.14-18本文将主要研究SFG和DFG.近年来,和频光谱研究的重要进展主要体现在和频光谱的偏振选择定则和实验构型分析等定量分析方面.

和频光谱的偏振选择定则是和频光谱指认的基础.在SFG-VS(DFG-VS)的实验过程中,由一束波长固定的可见激光与一束波长可调谐的红外激光同时同点入射到样品表面,在反射方向上产生一束频率为两束入射激光频率之和的和频光信号(产生频率之差的信号则为差频光信号).控制入射光与和频(差频)信号的偏振方向,如p方向或s方向(即光电场方向平行或垂直于入射面),扫描给定偏振的红外光(p光或s光)波长,获得和频(差频)振动光谱;这三束光的特定偏振方向的组合,简称为和频(差频)振动光谱的偏振组合.按文献惯例,偏振组合依和频(差频)、可见和红外的顺序命名.例如ssp表示和频(差频)信号s偏振方向,可见入射激光s偏振方向,红外入射激光p偏振方向.对于和频光谱,不同的偏振组合,会给出不同的光谱形状.利用这些信息,对分子振动模式进行分析和归属,这就是近年来发展起来的和频振动光谱的偏振选择定则.19-31

和频振动光谱的实验构型分析是定量研究和频光谱的基础.在实验测量上,SFG-VS(DFG-VS)广泛应用的有两种共面的实验构型:共向式实验构型和对射式实验构型.其定义是:可见光与红外光从界面法线同侧入射为共向式实验构型;两束入射光从法线两侧入射为对射式实验构型.这两种实验构型各有所长.由于共向式构型中信号发散角相对较小,大多数实验室采用共向式实验构型;然而,在对隐埋界面的研究中,对射式实验构型可以降低背景信号及非共振项的影响,所以也有些研究组采用对射式实验构型.Fourkas研究组32对于对射式实验构型研究此类界面的优点有较详细的论述.但不论对哪一种实验构型,可见和红外的入射角对SFG和DFG光谱都有很大的影响.它不但影响某个特定振动模式的强度,也影响其相位.固定两种共面的实验构型,适当改变入射角,就可以有针对性地研究某一个感兴趣的振动模式信号的大小和相位,使其相对强度变大,峰变得明显.这就是和频光谱的实验构型分析.24,25在我们以前的研究中,实验构型分析特指这两种实验构型下(主要是共向式)入射激光入射角的选择对光谱某个振动模式相对强度影响的分析.和频光谱的偏振选择定则和实验构型分析的引入,不仅使和频光谱定量研究界面问题成为可能,而且使和频光谱成为不再依赖拉曼和红外光谱的研究界面光谱的独立手段.22,25,29-31

实验构型分析方法有待进一步拓展和深入.如前所述,文献25中和频光谱实验构型的分析方法用于研究共向式实验构型下某些振动模式峰强度的相对大小与实验入射角之间的关系,但没有分析信号出射角与入射角之间的关系.后者对于和频光谱信号的采集效率同样非常重要.25因为,尽管从实验构型分析计算,当入射角改变到某一个特定的入射角,可以使某一个我们感兴趣的振动模式强度变大,但却有可能在反射的方向完全检测不到出射光的信号或者实验构型需要做大的调整才能检测到信号,这就必然会影响到信号的检测效率(后边我们将要说明,在和频光谱采用共向式实验构型下,会减少这种不便和麻烦);在搭建实验仪器时,我们首先要决定的是选择共向式和对射式两种构型中的哪种构型,既利于改变入射角增加某一个振动模式的信号强度,又能在信号出射方向方便并高效率地检测信号光.在以前的和频光谱实验构型分析中,并没有涉及到对射式实验构型.尽管实验构型分析的方法对于共向式和对射式并无原则的区别,但正如我们在下面将要证明的,从检测到信号光效率的角度考虑,这两种实验构型下入射光入射角的选择范围有很大的差别;DFG也有相应的构型分析(入射角对某一振动峰信号相对强度的影响),但在我们以往的工作中完全没有涉及.近来DFG方法研究界面有逐渐增加的趋势,发展DFG的实验构型分析并研究入射角对信号出射角的影响也显得很有必要.除此之外,频率对出射角的影响也很大,这也是现有的实验构型分析中未加考虑的一个重要因素.

应当强调的是,入射光的角度对某个振动模式强度和出射信号检测效率的影响是同等重要的,前者已有文献25进行过充分的阐述,本文的重点在后者.

综上所述,在和频(差频)光谱实验中,要选择一个有利于实验构型分析和信号采集的实验构型,首先必须仔细分析实验中红外和可见光的入射角、频率与和频(差频)的出射角之间的关系.根据这些关系,就可以选出一个最佳的实验构型.Tadjeddine研究组17,18曾对电极表面吸附分子界面的和频与差频光谱中信号出射角和相位匹配条件进行过较为深入的研究,但对于红外和可见光的入射角、频率与和频(差频)的出射角之间的关系,文献中还未见详细系统的报道.

本文对两种共面的SFG-VS和DFG-VS的实验构型(共向式实验构型和对射式实验构型)进行模拟研究.通过改变入射光的入射角和入射频率分析出射角的变化规律.结果证明在用和频(差频)光谱进行实验构型分析时,除考虑某一振动峰的强度与入射角的关系外,还应当考虑出射角的方向而选择一个最佳的检测角度,后者在实验仪器的搭建中更是首先应当考虑的.

2 理论分析

图1 和频及差频振动光谱过程的能级跃迁图Fig.1 Schematic transitions for SFG-VS and DFG-VS(a)schematic transitions for SFG-VS.(b)schematic transitions for DFG-VS.|g〉,|s1〉,and|s2〉are the vibrational ground state, vibrational excited state,and virtual state,respectively.ωSFG(ωDFG), ωvis,and ωIRare the frequencies of the SF(DF)signal,visible, and IR laser beam,respectively.

在通常的皮秒和频光谱激光系统中(本文主要讨论皮秒和频光谱,其模拟方式也能推广到宽带飞秒和频系统),固定ωvis=18797 cm-1(对应于绿光λvis= 532 nm),扫描红外光波长,得到和频(差频)光谱.红外光ωIR的变化范围为1000-4000 cm-1之间,因此ωSFG在19797-22797 cm-1范围内变化,而ωDFG在14797-17797 cm-1范围内变化.

图2(a)和图2(b)分别是SFG-VS共向式和对射式两种实验构型的示意图.图中Ωvis和ΩIR分别是ωvis和ωIR的入射角,ΩSFG为ωSFG的出射角,p和s分别表示光偏振方向平行和垂直入射面.DFG-VS共向式和对射式两种实验构型的示意图与图2相似.

SFG-VS与DFG-VS不仅能量守恒,且水平方向(图2中x轴)的动量守恒,即入射光总能量与出射光能量相同,且水平方向入射光总动量和出射光动量也相同.33,34通过上述两个守恒条件可以定量分析SFG-VS和DFG-VS的出射光的方向.

由图1(a)可知,SFG-VS能量守恒表示为

即

对图2所示的实验构型,SFG-VS水平方向动量守恒可表示为

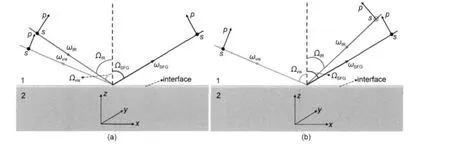
图2 SFG-VS实验构型图Fig.2 Experimental configuration of SFG-VS(a)co-propagation configuration.(b)counter-propagation configuration.Two incident beams,ωvisand ωIR,simultaneously overlap at the interface from medium 1 with the input angles Ωvisand ΩIR,respectively,and SFG signal at the frequency ωSFGis generated from the interface with an angle ΩSFG.The refraction index of frequency ωi(i=vis,IR,SFG)in medium 1 and medium 2 are n1(ωi)and n2(ωi). The plane of incidence is the p plane,and s direction is perpendicular to the p plane inward(the⊗sign)or outward(the●sign).

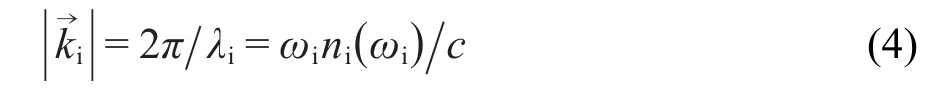
ni(ωi)是频率为ωi的光在传播介质中的折射率,c为真空中的光速.

由图1(b)可知,DFG-VS能量守恒可表示为

即

DFG-VS水平方向动量守恒也可表示为

我们分以下几种情况,对公式(3)和公式(7)进行展开讨论.首先考虑SFG-VS的情况.

2.1 共向式实验构型SFG

共向式实验构型仅考虑SFG信号在法线右侧出射的情况.由公式(3)可知,和频光不可能出现在法线的左侧,因为此时水平方向上动量不守恒.

对于共向式实验构型,当和频光出射在法线右侧时,公式(3)可展开为

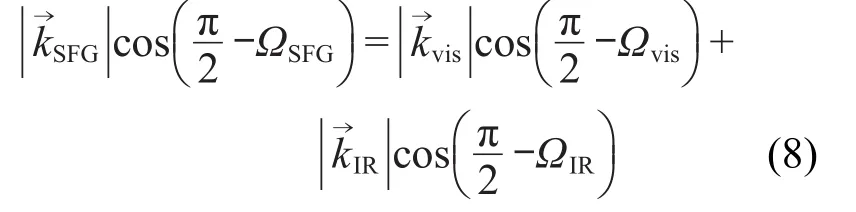
化简,得

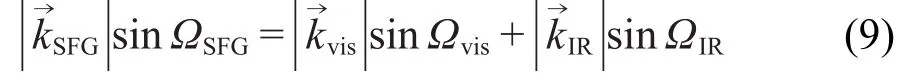
将公式(4)代入公式(9)中,并考虑到ωvis、ωIR和ωSFG的光在同种介质中折射率n(ω)相差很小,两边约去折射率,便得出共向式实验构型出射角ΩSFG表达式为

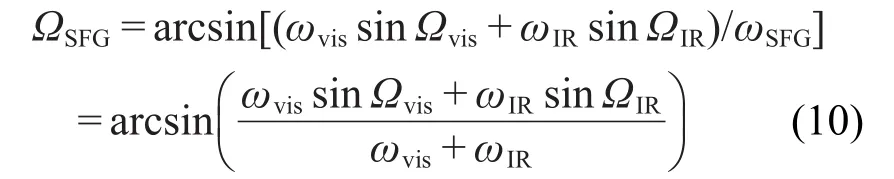
2.2 对射式实验构型SFG

对射式实验构型分为和频光在法线右侧和法线左侧出射两种情况.

2.2.1 和频光在法线右侧出射

对于对射式实验构型,当和频光在法线右侧出射时,公式(3)可展开为

化简,得

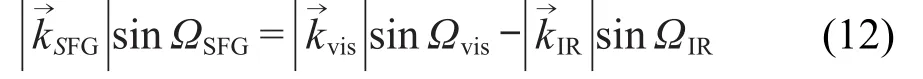
同理,可得对射式实验构型和频光在法线右侧出射时的出射角为

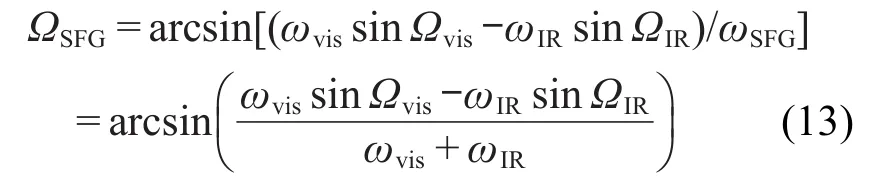
2.2.2 和频光在法线左侧出射

对于对射式实验构型,当和频光在法线左侧出射时,公式(3)可展开为

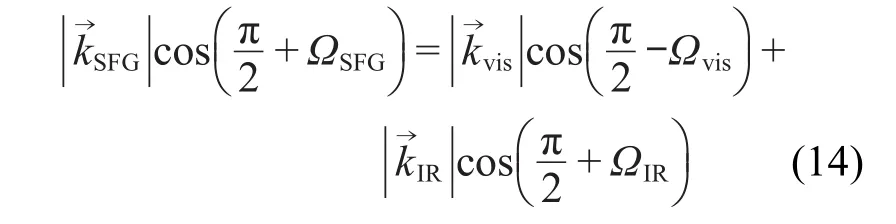
化简,得

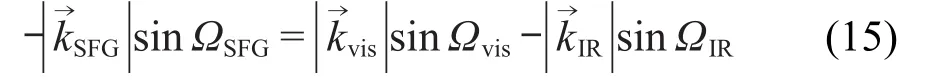
同理,可得对射式实验构型和频光在法线左侧出射时的出射角为

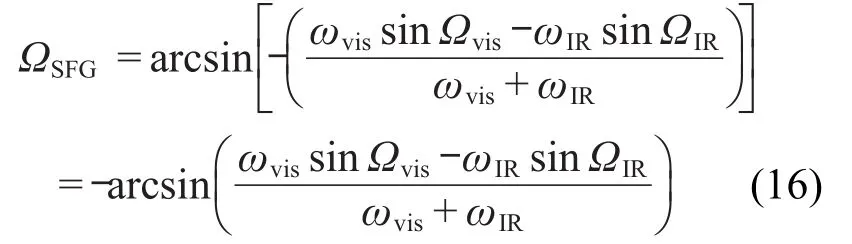
从公式(13)和公式(16)的表达式可以看到,在相同的入射角条件下,用公式(13)求出的在法线右侧出射的和频光出射角和用公式(16)求出在法线左侧出射的和频光出射角大小相等,符号相反.公式(13)和公式(16)反映了同样的物理事实.因此,下面讨论对射式实验构型的和频光出射角时采用公式(13).

下面展开公式(7),讨论两种实验构型时DFG信号出射角的表达式.对于DFG,用前面相同的方法,也有类似的公式.

共向式实验构型DFG:

对射式实验构型DFG:

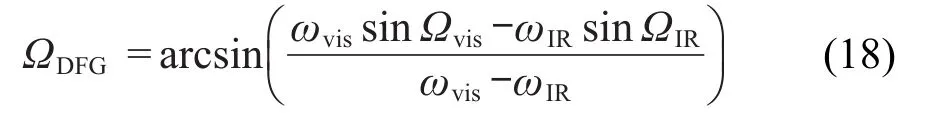
由公式(10)、(13)、(17)和(18)可知,信号出射角ΩSFG和ΩDFG与入射光频率ωvis和ωIR及入射角Ωvis和ΩIR有关.首先,我们根据以上公式讨论能够检测出信号光的条件.

由公式(10)可知,共向式ΩSFG是反正弦函数,因此,公式(10)中ΩSFG有解(即在实验中能够检测到SFG信号)的必要条件是

同理,公式(13)、(17)和(18)中相应出射角有解的必要条件依次是

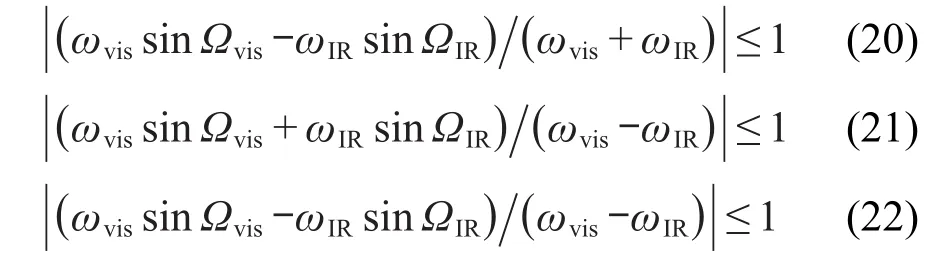
从不等式(19)和(20)可以看出,对任意给定的频率ωvis和ωIR,入射角Ωvis和ΩIR取任意值时,不等式总成立.因此SFG-VS共向式和对射式两种实验构型, Ωvis和ΩIR取0°-90°的任意值,都可以在实验上观察到和频信号,而与入射光的频率无关.即在此范围的任何入射光的入射角组合,都能产生出射角合理的(可检测)和频光.

对DFG-VS,使不等式(21)和(22)成立的Ωvis和ΩIR的取值范围是非常复杂的,它依赖于入射光频率的选择.此时,差频光的出射角度与入射光的入射角和入射光的频率呈现复杂的关系.必须进行有关的数值模拟才能明了.

下面我们分三种情况,对信号出射角ΩSFG和ΩDFG与入射光频率ωvis和ωIR及入射角Ωvis和ΩIR之间的关系进行模拟:

(1)入射激光的频率给定,讨论可检测到出射信号时入射角度的允许范围;

(2)入射激光的频率给定,讨论可检测到出射信号时出射角与入射角之间的关系;

(3)在入射角允许范围内,对于特定的入射角和特定的入射可见光的频率,讨论两种实验构型下扫描红外频率,出射角随红外频率的变化关系.

3 结果与讨论

3.1 有出射信号时入射角度的允许范围

当给定入射光频率时,对不等式(19)、(20)、(21)和(22)进行求解,可以得到共向式和对射式两种实验构型下可检测到出射信号时入射光角度的允许范围.

当ωvis=18797 cm-1(这是皮秒和频及差频光谱实验系统中常用的固定可见光的频率),ωIR=3000 cm-1,共向式和对射式两种实验构型下可检测到出射信号时Ωvis和ΩIR的允许范围如图3所示.图中,区域I表示和频信号(差频信号)从法线左侧出射,即出射角ΩSFG≤0°(ΩDFG≤0°)时,入射角的允许范围;区域II表示和频信号(差频信号)从法线右侧出射,即出射角ΩSFG≥0°(ΩDFG≥0°)时,入射角的允许范围;区域III表示这些入射角组合时检测不到出射信号(差频信号).对于SFG-VS共向式实验构型,Ωvis和ΩIR取0°-90°之间任意值时,始终都可在法线右侧检测到和频出射信号,故图3中没有给出其允许范围的图. SFG-VS对射式实验构型时Ωvis与ΩIR的允许范围如图3(a)所示,对于对射式实验构型,选取不同的入射角组合会在界面法线的不同侧出现和频信号,这对于实验构型分析极为不利.因为有利于某一个振动模式的入射角组合,可能使得出射光完全改变方向,这需要改变实验平台结构,对检测光路进行重大的调整才能办到.比较SFG-VS共向式和对射式实验构型可知,在不改变实验平台结构的前提下,即能在法线右侧检测到和频信号时,共向式实验构型入射角的允许范围比对射式实验构型要大,因此对于SFG-VS,共向式实验构型更有利于SFG实验入射角的选取和信号的采集.DFG-VS共向式和对射式实验构型时Ωvis与ΩIR的允许范围如图3(b)和3 (c)所示.

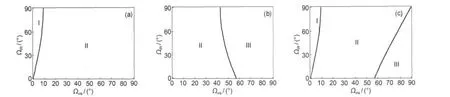
图3 可检测到出射信号的入射角范围Fig.3 Range of incident angles with detectable signalRange of incident angles Ωvisand ΩIRwith detectable signal.The frequencies of visible and IR laser beams are 18797 cm-1and 3000 cm-1, respectively.(a)counter-propagation of SFG-VS.(b)co-propagation of DFG-VS.(c)counter-propagation of DFG-VS.When the range of Ωvisand ΩIRare in the areas I and II,the signal is generated from the left and right of the normals.When the ranges of Ωvisand ΩIRare in the area III,there will be no signal(DFG signal).

此外,比较图3(b)和图3(c)可知,能在法线右侧检测到差频信号时,对射式实验构型入射角的允许范围比共向式实验构型要大,且对射式实验构型入射角取值范围在图中对角线两侧均匀分布.因此对射式实验构型有利于DFG实验入射角的选取及实验平台的搭建和实验测量.从图3中还可以看出, SFG-VS在对应的实验构型下入射角取值范围比DFG-VS要大得多.

通过对不等式(19)、(20)、(21)和(22)进行分析,可知对于SFG-VS,共向式实验构型入射角的允许范围更大,因此共向式实验构型更有利于SFG实验入射角的选取及实验平台的搭建;对于DFG-VS,对射式实验构型入射角的允许范围更大,因此对于实验信号采集对射式实验构型更为有利.

3.2 出射角与入射角的关系

当给定入射光频率时,利用公式(10)、(13)、(17)和(18)进行模拟,可以得到共向式和对射式两种实验构型下可检测到出射信号的出射角ΩSFG和ΩDFG与入射光角度之间的关系.

比如,当ωvis=18797 cm-1,ωIR=3000 cm-1时,ΩSFG和ΩDFG随Ωvis和ΩIR的变化如图4所示.图4中最粗的虚线是ΩIR=0°(对应于实验中红外光垂直入射)的情况;其左边的三条虚线对于共向式实验构型;其右边的三条虚线对应于对射式实验构型.图4(a)和4 (b)中的实线表示可见光的反射光与出射光共线的共线式实验构型,其入射角与出射角的关系为ΩSFG(ΩDFG)=Ωvis=ΩIR.从图4(a)中可知,实线只与共向式实验构型的虚线相交,故SFG-VS只有在共向式实验构型时才有共线式实验构型(共线式实验构型也是非线性光学实验中经常采用的实验构型).从图4(b)中可知,DFG-VS只有在对射式实验构型时才有共线式实验构型.图4中纵坐标(即ΩSFG或ΩDFG)小于零的部分,即水平虚线以下部分,对应于信号光从图2中法线左侧出射的情况.

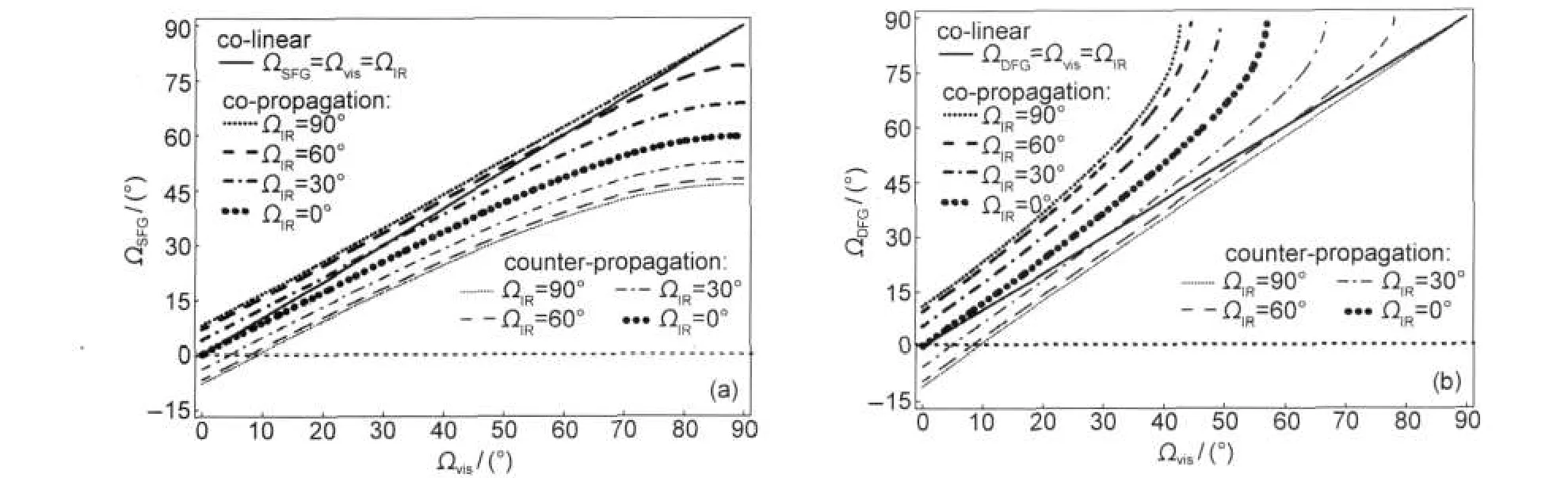
图4 出射角随入射角的变化图Fig.4 Signal output angle as a function of incident anglesThe relative output angles ΩSFGand ΩDFGas a function of Ωvisat certain input IR angles ΩIRwith ωvis=18797 cm-1and ωIR=3000 cm-1. (a)SFG-VS.(b)DFG-VS.The output angle greater than zero(above the level)or less than zero(below the level) indicates that the signal is generated from the right or left of the normals,respectively.

图4(a)中SFG-VS的任意ΩIR曲线的横坐标(即Ωvis)范围都是0°-90°,即当SFG-VS的实验构型为共向式或对射式时,Ωvis和ΩIR都可取0°-90°任意值,这与不等式(19)和不等式(20)预言的结果一致.这是以前我们31在实验构型分析中遇到的情形.这也可以理解为什么当时并没有考虑入射角对采集信号的影响.对于DFG-VS,除对射式实验构型中ΩIR=90°的曲线以外,任意曲线的横坐标取值范围都比0°-90°要小,例如,图中ΩIR=0°曲线,Ωvis的变化范围为0°-57.2°.即DFG-VS共向式和对射式实验构型,Ωvis和ΩIR的选择范围比较窄,这与图3所得结论一致.

在和频(差频)光谱仪器的搭建中,可见反射光也是决定实验构型的一个重要的因素,可见反射光与出射信号光差别越大,越利于实验的滤波.在图3允许的入射角组合范围内,对和频光谱及差频光谱中可见光的反射光和信号光的出射角进行模拟比较,结果如图5所示.

当ωvis=18797 cm-1,ωIR=3000 cm-1,可见光的入射角分别取为30°、45°和60°时(30°-60°是目前和频光谱实验中可见光入射角普遍选取的范围),和频光谱两种实验构型的信号出射角随红外光入射角的变化如图5(a)所示,图中三条水平实线分别表示可见光反射角为30°、45°和60°.从图5(a)中可以看出,无论红外光入射角如何变化,共向式实验构型中信号光出射角与可见光反射角总是差别不大,而对射式实验构型中两者的差别较共向式实验构型较大,该结论与Fourkas等32的研究结果相符.

当ωvis=18797 cm-1,ωIR=3000 cm-1,可见光的入射角分别取为20°、35°和50°时(20°-50°范围是在图3允许的入射角组合范围内选取的),差频光谱两种实验构型的信号出射角随红外光入射角的变化如图5(b)所示,图中三条水平实线分别表示可见光出射角为20°、35°和50°.从图5(b)中可知,无论红外光入射角如何变化,共向式实验构型中信号光与可见光的反射光在出射方向的差别较对射式实验构型更大.

3.3 出射角与入射光频率的关系

对于SFG-VS(DFG-VS)的共向式和对射式两种实验构型,当Ωvis、ΩIR及ωvis给定,扫描ωIR时,信号出射角会随ωIR变化.若在某种实验构型下扫描ωIR时,SFG(DFG)信号出射角随ωIR的变化范围大,将明显影响所获光谱的准确性,因为在获取偏振光谱过程中,不可能随时调整检测系统.因此这种实验构型就不利于信号采集.为了更加准确地采集信号并进一步提高信号采集效率,对信号出射角随ωIR变化进行定量分析有很重要的意义.下面分四种情况对SFG(DFG)信号出射角随ωIR的变化关系进行分析,其中入射角度在可检测到出射信号的允许范围内选取.

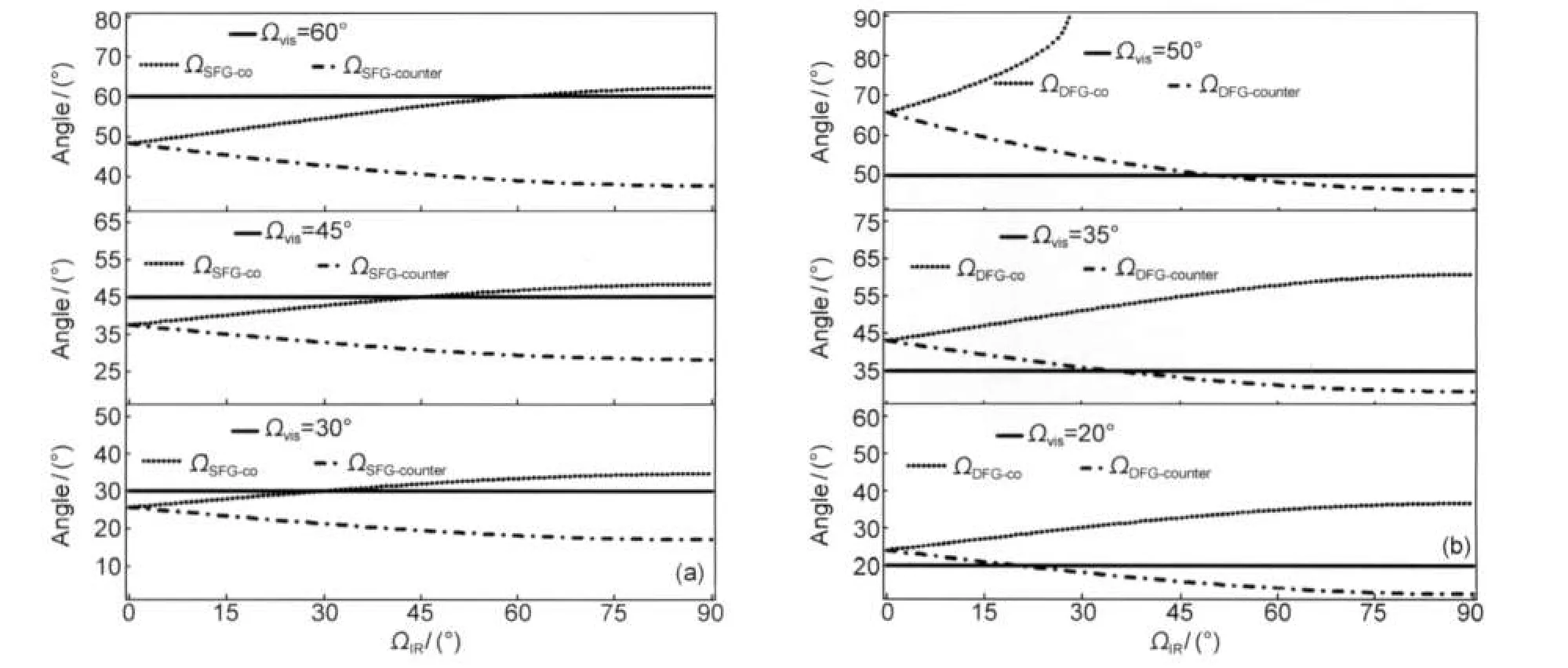
图5 可见光的反射角和信号光的出射角比较图Fig.5 Comparison of the reflection angle of visible light with the output angle of the signalThe relative reflected angle of visiable light,the output angle of co-propagation,counter-propagation as a function of ΩIRat certain different input angle Ωviswith ωvis=18797 cm-1and ωIR=3000 cm-1.(a)SFG-VS.(b)DFG-VS.In Fig.5(a),the input angle Ωvisis 30°,45°,and 60°, respectively.In Fig.5(b),the input angle Ωvisis 20°,35°,and 50°,respectively.

(1)ωvis=18797 cm-1,Ωvis=60°,ΩIR在0°-90°之间取值,两种实验构型下ΩSFG随ωIR变化(1000-4000 cm-1)关系如图 6所示.图中ωIR的变化范围(1000-4000 cm-1)是目前大多数皮秒和频激光系统检测的最佳红外波长变化范围,比如,经常检测的CH3、CH2和OH等基团对称和反对称振动模式就在此范围内.从图6(b)中可见,无论ΩIR取何值,对射式实验构型ΩSFG随ωIR变化的范围都很大,例如图中ΩIR=45°曲线,ΩSFG改变了15.7°(51.9°-36.2°).因此SFG-VS的对射式实验构型,不利于SFG信号的采集.而对于共向式实验构型,相同条件下ΩSFG随ωIR变化的范围较小,例如图6(a)中ΩIR=45°的曲线,ΩSFG改变了2.2°(59.1°-56.9°).因此对SFG-VS,从采集信号效率而言,实验中选取共向式实验构型更有利于SFG信号的采集.此外,比较图6(a)和图6(b)还可看出,无论红外光频率如何选取,共向式实验构型中信号光出射角与可见光的反射角(为60°)总是差别不大,而对射式实验构型中两者要分得更开.

图6 不同红外光入射角时SFG出射角随红外光频率变化图Fig.6 Output angle of SFG as a function of IR frequency with the different incident angles of IRThe relative SFG-VS signal output angle of co-propagation and counter-propagation as a function of ωIRat certain different ΩIRwith ωvis=18797 cm-1and Ωvis=60°.(a)co-propagation of SFG-VS. (b)counter-propagation of SFG-VS.

(2)ωvis=18797 cm-1,ΩIR=50°,Ωvis在0°-90°之间取值,共向式实验构型下ΩSFG随ωIR变化(1000-4000 cm-1)关系如图7所示.从图中可知ΩSFG随ωIR变化范围都在Ωvis附近,例如图中Ωvis=45°曲线的ΩSFG变化范围为45.2°-45.8°.比较图6中共向式实验构型和图7可知,共向式实验构型Ωvis对ΩSFG取值的影响较ΩIR要大.

(3)ωvis=18797 cm-1,Ωvis=30°,ΩIR在0°-90°之间取值,两种实验构型下ΩDFG随ωIR变化(1000-4000 cm-1)关系如图8所示.无论ΩIR取何值,共向式实验构型ΩDFG随ωIR的变化范围都相对较大,例如图8中ΩIR=45°的曲线ΩDFG改变了21.1°(34.6°-55.7°).对射式实验构型,当ΩIR与Ωvis相差不多时,ΩDFG随ωIR的变化范围比较小.因此对DFG-VS而言,共向式实验构型不利于信号采集,在选取合适的Ωvis和ΩIR组合时对射式实验构型更有利于信号的采集.此外,比较图8(a)和图8(b)还可知,无论红外光频率如何选取,共向式实验构型中信号光与可见光的反射光在出射方向的差别(可见光反射角为30°)比对射式实验构型大.

(4)ωvis=18797 cm-1,ΩIR=20°,Ωvis在5°-55°之间取值(取值范围由图3(c)决定),对射式实验构型下ΩDFG随ωIR变化(1000-4000 cm-1)关系如图9所示.比较图8中对射式实验构型和图9可知,对射式实验构型Ωvis对ΩDFG取值的影响比ΩIR要大得多.

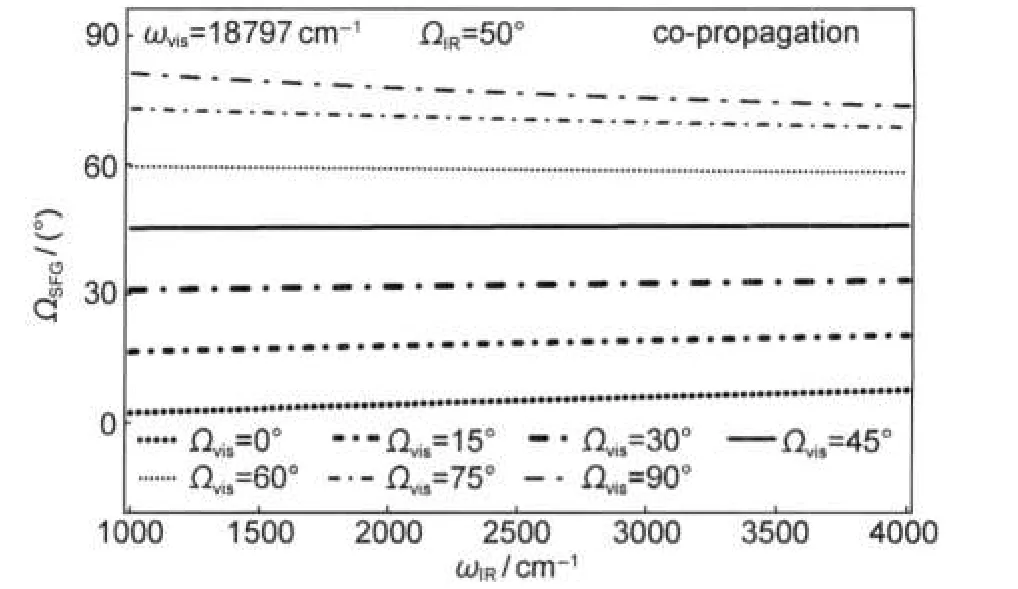
图7 不同可见光入射角时SFG出射角随红外光频率变化图Fig.7 Output angle of SFG as a function of IR frequency with the different incident angles of visible lightThe relative SFG-VS output angle of co-propagation as a function of ωIRat certain different Ωviswith ωvis=18797 cm-1and ΩIR=50°.

通过上述分析,SFG(DFG)信号出射角随ωIR的变化关系如下:(1)ωvis、Ωvis和ΩIR给定时,共向式实验构型的ΩSFG随ωIR的变化范围比对射式实验构型小; (2)共向式实验构型时,Ωvis的改变对ΩSFG取值的影响比ΩIR大,因此ΩSFG的值更多的取决于Ωvis的取值; (3)ωvis、Ωvis和ΩIR给定时,共向式实验构型的ΩDFG随ωIR的变化范围比对射式实验构型大,因此对射式实验构型更有利于DFG信号的采集;(4)对射式实验构型时,Ωvis的改变对ΩDFG取值的影响比ΩIR大,因此ΩDFG的值更多的取决于Ωvis的取值.

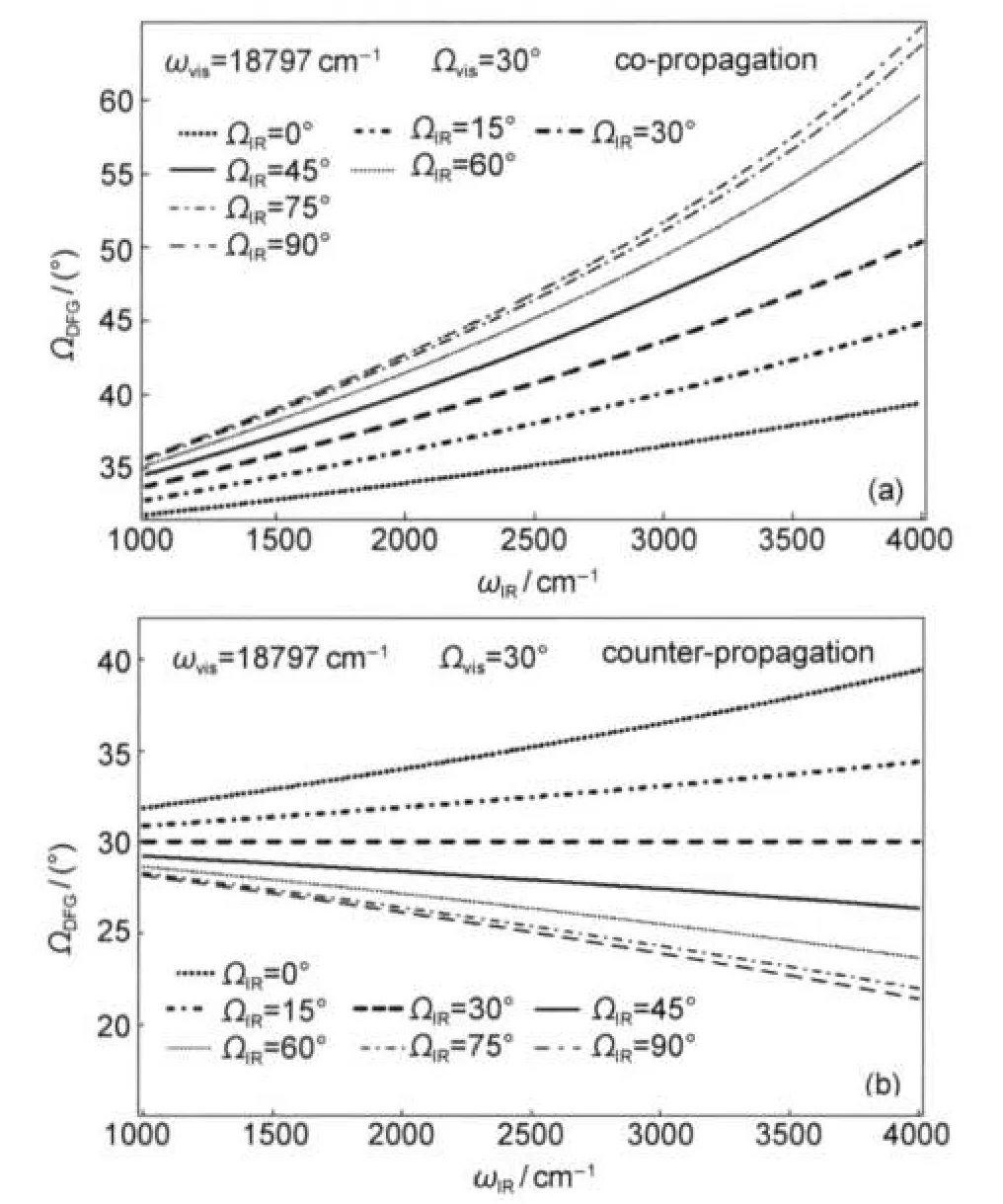
图8 不同红外光入射角时DFG出射角随红外频率变化图Fig.8 Output angle of DFG as a function of IR frequency with the different incident angles of IRThe relative DFG-VS output angle of co-propagation and counter-propagation as a function of ωIRat certain different ΩIR with ωvis=18797 cm-1and Ωvis=30°.(a)co-propagation of DFG-VS. (b)counter-propagation of DFG-VS.

3.4 两种实验构型的比较

通过上述对信号出射角ΩSFG和ΩDFG与入射光频率ωvis和ωIR及入射角Ωvis和ΩIR之间关系的分析,可将和频光谱中的共向式实验构型和对射式实验构型的优缺点总结如下:

(1)相同条件下,采用共向式实验构型时可见光和红外光的入射角允许范围大,可选取的入射角组合更多,而采用对射式实验构型时入射角允许范围较小,能够选取的入射角组合少,此为共向式实验构型的优点一;

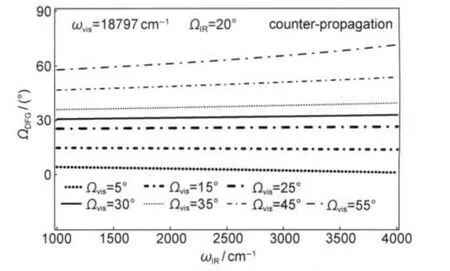
图9 不同可见光入射角时DFG出射角随红外光频率变化图Fig.9 Output angle of DFG as a function of IR frequency with the different incident angle of visable lightThe DFG-VS relative output angle of counter-propagation as a function of ωIRat certain different Ωviswith ωvis=18797 cm-1and ΩIR=20°.

(2)相同条件下扫描红外光频率时,采用共向式实验构型的信号光出射角的改变较小,而采用对射式实验构型的信号光出射角的改变却较大,此为共向式实验构型的优点二;

(3)相同条件下,无论是红外光的入射角还是红外光的频率如何改变,对射式实验构型中信号光与入射光的反射光在出射方向的差别都比共向式实验构型要大,有利于信噪比的提高,该优势对于隐埋界面更加明显.因为在该体系中非共振的背景信号由可见光的反射光和体相介质的电四极矩的贡献两部分组成,对射式构型中,信号光和入射光的反射光分的更开,可以更有效地避免可见光的反射光对信号光的影响,此外对射式实验构型中两束入射光光斑重叠的空间相对共向式实验构型较小,因此产生的电四极矩的非共振背景信号也更小,有利于提高信噪比及得到更准确的光谱.32

对于差频光谱中的共向式实验构型和对射式实验构型的优缺点总结如下:

(1)相同条件下,采用对射式实验构型时可选取的入射角组合更多,而采用共向式实验构型时能够选取的入射角组合较少,此为对射式实验构型的第一个优点;

(2)相同条件下扫描红外光频率时,采用对射式实验构型的信号光出射角的改变较小,而采用共向式实验构型的信号光出射角的改变却大很多,此为对射式实验构型的第二个优点;

(3)相同条件下,无论是红外光的入射角还是红外光的频率如何改变,共向式实验构型中信号光与入射光的反射光在出射方向的差别比对射式实验构型要大,有利于提高信噪比.

4 结论

利用非线性相干光学过程能量守恒和水平方向动量守恒的性质对二阶非线性相干光学过程SFG-VS和DFG-VS的出射角进行理论分析,得到出射角只与入射角及入射光频率有关,具体关系如公式(10)、(13)、(17)和(18)所示.

通过对公式(10)和(13)的分析与模拟得到SFG-VS出射角与入射角及入射频率之间的关系如下:(1)无论共向式还是对射式实验构型,Ωvis和ΩIR任意取值都有出射信号产生,在考虑ΩSFG≥0°时,共向式入射角取值范围比对射式要大;(2)给定Ωvis和ΩIR,共向式ΩSFG随ωIR变化的范围比对射式要小得多;(3)共向式实验构型时,Ωvis对ΩSFG取值的影响比ΩIR大.

对公式(17)和(18)进行分析与模拟,得到DFG-VS出射角与入射角及入射频率之间的关系如下:(1)无论共向式还是对射式实验构型,Ωvis和ΩIR的取值都有限制,在考虑ΩDFG≥0°时,对射式实验构型入射角取值范围比共向式实验构型要大,且对射式入射角取值范围更加对称;(2)给定Ωvis和ΩIR,对射式ΩDFG随ωIR变化的范围比共向式要小;(3)对射式实验构型时Ωvis对ΩDFG取值的影响比ΩIR要大.

通过仔细分析实验中红外和可见光的入射角、频率与和频(差频)的出射角之间的关系,详细分析了皮秒SFG-VS及DFG-VS实验中两种实验构型的区别,得到了SFG-VS及DFG-VS的出射角与入射角及入射频率之间的关系.一般的气/液、气/固SFG-VS实验中采用共向式实验构型不仅有利于信号的采集,同时在搭建实验平台时还可以有更多的入射角进行选择,以便用实验构型分析的理论对光谱进行定量分析分析;对于隐埋界面的SFG实验,采用对射式实验构型,在降低背景信号提高信噪比上更有优势;对于DFG-VS,实验中采用对射式实验构型,便于实验入射角的选取及差频信号的采集.上述结论对实验信号的准确测量及对实验信号的定量分析有重要的意义.

(1)Adamson,A.W.;Gast,A.P.Physical Chemistry of Surfaces,6th ed.;Wiley:New York,1997.

(2) Menzel,D.Science 2002,295,58.

(3) Stevens,M.M.;George,J.H.Science 2005,310,1135.

(4) Sanvito,S.Nature 2010,467,664.

(5) Somorjai,G.A.Chem.Rev.1996,96,1223.

(6) Shen,Y.R.Nature 1989,337,519.

(7) Shen,Y.R.Annu.Rev.Phys.Chem.1989,40,327.

(8) Shultz,M.J.;Schnitzer,C.;Simonelli,D.;Baldelli,S.Int.Rev. Phys.Chem.2000,19,123.

(9) Eisenthal,K.B.Chem.Rev.1996,96,1343.

(10) Miranda,P.B.;Shen,Y.R.J.Phys.Chem.B 1999,103,3292.

(11) Richmond,G.L.Chem.Rev.2002,102,2693.

(12) Shen,Y.R.;Ostroverkhov,V.Chem.Rev.2006,106,1140.

(13)Wang,H.F.;Gan,W.;Lu,R.;Rao,Y.;Wu,B.H.Int.Rev.Phys. Chem.2005,24,191.

(14) Pluchery,O.;Humbert,C.;Valamanesh,M.;Lacaze,E.;Busson, B.Phys.Chem.Chem.Phys.2009,11,7729.

(15) Le Rille,A.;Tabjeddine,A.;Zheng,W.Q.;Peremans,A.Chem. Phys.Lett.1997,271,95.

(16)Mendoza,B.S.;Mochan,W.L.;Maytorena,J.A.Phys.Rev.B 1999,60,14334.

(17) Tadjeddine,A.;Le Rille,A.;Pluchery,O.;Vidal,F.;Zheng,W. Q.;Peremans,A.Phys.Stat.Sol.1999,175,89.

(18) Le Rille,A.;Tadjeddine,A.J.Electroanal.Chem.1999,467, 238.

(19) Rao,Y.;Tao,Y.S.;Wang,H.F.J.Chem.Phys.2003,119,5226.

(20)Lu,R.;Gan,W.;Wu,B.H.;Chen,H.;Wang,H.F.J.Phys. Chem.B 2004,108,7297.

(21)Lu,R.;Gan,W.;Wu,B.H.;Zhang,Z.;Guo,Y.;Wang,H.F. J.Phys.Chem.B 2005,109,14118.

(22)Chen,H.;Gan,W.;Lu,R.;Guo,Y.;Wang,H.F.J.Phys.Chem. B 2005,109,8064.

(23)Gan,W.;Wu,B.H.;Chen,H.;Guo,Y.;Wang,H.F.Chem. Phys.Lett.2005,406,467.

(24)Gan,W.;Wu,D.;Zhang,Z.;Feng,R.R.;Wang,H.F.J.Chem. Phys.2006,124,114705.

(25)(a)Gan,W.;Wu,B.H.;Zhang,Z.;Guo,Y.;Wang,H.F.J.Phys. Chem.C 2007,111,8716. (b)Jena,K.C.;Hung,K.K.;Schwantje,T.I.;Hore,D.K. J.Chem.Phys.2011,135,044704

(26)Zheng,D.S.;Wang,Y.;Liu,A.A.;Wang,H.F.Int.Rev.Phys. Chem.2008,27,629.

(27) Wang,Y.;Cui,Z.F.;Wang,H.F.Chin.J.Chem.Phys.2007,20, 449.

(28) Wang,H.F.Chin.J.Chem.Phys.2004,17,362.

(29)Chen,H.;Gan,W.;Wu,B.H.;Wu,D.;Guo,Y.;Wang,H.F. J.Phys.Chem.B 2005,109,8053.

(30)Gan,W.;Wu,D.;Zhang,Z.;Guo,Y.;Wang,H.F.Chin.J. Chem.Phys.2006,19,20.

(31)Gan,W.;Zhang,Z.;Feng,R.R.;Wang,H.F.J.Phys.Chem.C 2007,111,8726.

(32) Ding,F.;Zhong,Q.;Brindza,M.R.;Fourkas,J.T.;Walker,R. A.Opt.Exp.2009,17,14665.

(33) Boyd,R.W.Nonlinear Optics,2nd ed.;Wiley:New York,2003; p 8.

(34) Bloembergen,N.;Pershan,P.S.Phys.Rev.1962,128,606.

May 25,2011;Revised:September 19,2011;Published on Web:October 19,2011.

Analysis and Simulation of Experimental Configurations for Sum Frequency Generation and Difference Frequency Generation Vibrational Spectroscopy

WANG Yuan1DENG Gang-Hua2GUO Yuan2,*
(1Technology College,Hainan University Sanya College,Sanya 572022,Hainan Province,P.R.China;2State Key Laboratory of Molecular Reaction Dynamics,Institute of Chemistry,Chinese Academy of Sciences, Beijing 100190,P.R.China)

The analysis of experimental configurations is the foundation for quantitative analysis in sum frequency generation vibrational spectroscopy(SFG-VS).The incident angles affect the signal intensity of some modes of vibration and the detection efficiency of the SFG signal.However,the issue of detection efficiency has not been included in previous experimental configuration analysis studies.According to the principle of the conservation of energy and momentum in coherent optics we simulated and analyzed the effect of incident angles,frequency of the incident light,and other factors on the output signal angle of difference frequency generation vibrational spectroscopy(DFG-VS)and SFG-VS.We intended to determine the reasonable and effective experimental configurations with more combinations of incident angles and less dispersion of the signal output angle.We found that SFG-VS with the co-propagation experimental configuration and DFG-VS with the counter-propagation experimental configuration favour the collection of the signal and quantitave analysis of the SFG-VS and DFG-VS.

Nonlinear optics;Experimental configuration analysis;Sum frequency generation vibrational spectroscopy;Difference frequency generation vibrational spectroscopy

10.3866/PKU.WHXB20112733

∗Corresponding author.Email:guoyuan@iccas.ac.cn;Tel:+86-10-62555347.

The project was supported by the National Natural Science Foundation of China(91027042,21073199)and Main Direction Program of Knowledge Innovation of ChineseAcademy of Sciences(KJCX-EW-W09).

国家自然科学基金(91027042,21073199)和中国科学院知识创新工程重要方向性项目(KJCX-EW-W09)资助

O643;O437.1